Тепломассообмен методичка. Тепломассообмен Методические материалы для студентов Направление подготовки Теплоэнергетика и теплотехника Профиль Энергообеспечение предприятий Составитель доцент кафедры Энергетики и электротехнологии Артамонова Л.
 Скачать 0.85 Mb.
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Ижевская государственная сельскохозяйственная академия» Факультет непрерывного профессионального образования Тепломассообмен Методические материалы для студентов Направление подготовки – Теплоэнергетика и теплотехника Профиль - Энергообеспечение предприятий Составитель: доцент кафедры «Энергетики и электротехнологии» Артамонова Л.П. Ижевск 2020 ФГБОУ ВО Ижевская ГСХА Содержание 1. Общие методические указания………………………………………...………..3 2. Программа к изучению дисциплины....................................................................4 3. Вопросы для подготовки к экзамену………………………………...………….31 4. Задание для контрольной работы.........................................................................34 4.1. Методические указания к выполнению контрольной работы..................34 4.2. Вопросы для самоподготовки …………………...………………………..35 4.3. Задание к контрольной работе.....................................................................37 Приложения ………………………………………………………………………….42 Литература…………………………………………………………………………….44 1 ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ Методические указания составлены в соответствии с требованиями ФГОС ВО по направлению подготовки 13.03.01«Теплоэнергетика и теплотехника (уровень бакалавриата)», утвержденный приказом Минобрнауки РФ № 1081 от 1 октября 2015 г. По дисциплине выполняется контрольная работа по индивидуальным заданиям, которые приведены в настоящих методических указаниях. При изучении дисциплины студент овладевает теоретическими знаниями и практическими навыками по рациональному применению теплоты, эффективному использованию теплотехнического оборудования. В результате изучения дисциплины студент должен: уметь применять уравнения и справочную литературу для расчета различных задач тепломассообмена; уметь рассчитывать температурное поле и тепловые потоки в твердых телах, а также в потоке жидкости и газа; знать и уметь рассчитывать величины, характеризующие интенсивность процессов тепломассообмена; уметь анализировать различные факторы, влияющие на процессы тепломассообмена; уметь математически сформулировать конкретную задачу тепломассообмена и выполнить ее решение путем физического и математического моделирования; уметь выполнять тепловой расчет теплообменных аппаратов Курс «Тепломассообмен» рекомендуется изучать в последовательности, указанной в программе и методических указаниях. Необходимо разобраться в основных понятиях и определениях, которые, как правило, предшествуют выводу определенной формулы. 2 ПРОГРАММА К ИЗУЧЕНИЮ ДИСЦИПЛИНЫ «ТЕПЛОМАССООБМЕН» Тема 1. Основные понятия и определения Предмет и основные задачи теории. Место дисциплины в подготовке инженеров-энергетиков. Основные понятия и определения. Виды распространения теплоты: теплопроводность, конвекция и тепловое излучение. Сложный теплообмен. Понятие о массообмене. Тема 2. Теплопроводность при стационарном режиме Теплопроводность при стационарном режиме. Основной закон теплопроводности (закон Фурье). Дифференциальное уравнение теплопроводности. Условия однозначности. Теплопроводность через плоскую однослойную и многослойную стенки, цилиндрическую однослойную и многослойную стенки, шаровую стенку. Теплопроводность тел неправильной формы. Теплопроводность при наличии внутреннего источника теплоты. Основные формулы для решения практических задач Поверхностная плотностьтеплового потока q, Вт/м2 – тепловой поток, проходящий через единицу площади Fповерхности теплообмена; q=Q/F. Линейная плотностьтеплового потока ql, Вт/м – тепловой поток, отнесенный к единице длины Iцилиндрической трубы: ql =Q/l. Теплопроводностьматериала или коэффициент теплопроводности К, Вт/(м·0С) – величина, равная отношению поверхностной плотности теплового потока qк модулю температурного градиента: λ=q/|gradТ|. Среднеинтегральная теплопроводность в диапазоне температур 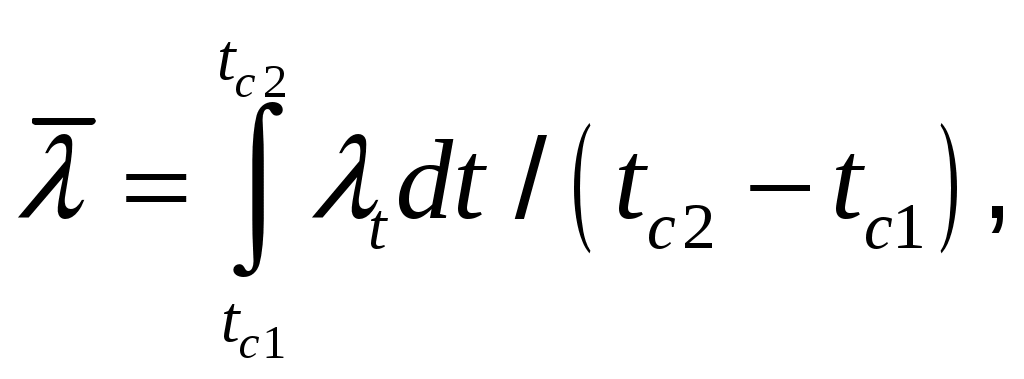 и  на поверхностях стенки где  –теплопроводность, зависящая от температуры.Зависимость теплопроводности от температуры t, °C, приближенно можно выразить в виде линейной функции где λ0 – теплопроводность при 0°С, Вт/(м·0С); b – постоянная, зависящая от природы материала и определяемая опытным путем, К-1. Величина  , при использовании зависимости принимает значение  , определяемое по среднеарифметической температуре стенки: Стационарная теплопроводность плоской стенки без внутренних источников теплоты. Температурное поле в однородной неограниченной стенке толщиной δ при   где х – текущая координата плоскости, в которой определяется температура  ,  .Температурное поле в стенке при линейном законе изменения теплопроводности от температуры (х – расстояние от поверхности стенки, имеющей температуру 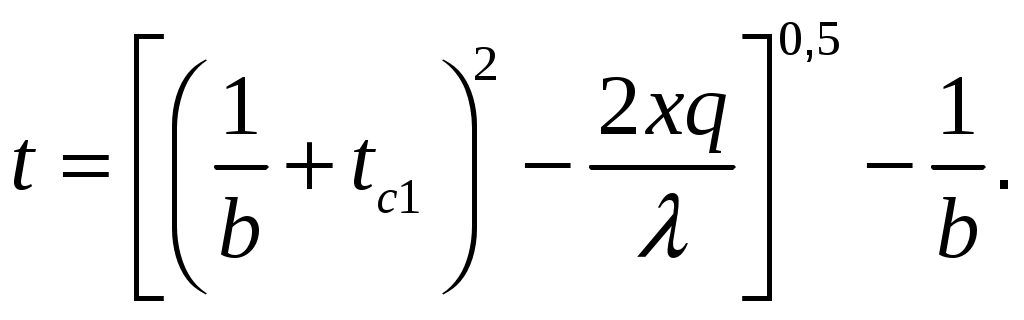) Формула теплопроводностидля стенки, составленной из п слоев различных материалов,  где и  – температуры на внешних поверхностях многослойной стенки, °С;  – толщина i-го слоя стенки, м; – теплопроводность материала i-го слоя стенки, Вт/(м·0С).Температура на поверхности плотно соприкасающихся между собой слоев в многослойной стенке  При расчете многослойных стенок можно воспользоваться эквивалентным коэффициентом теплопроводности  где – толщина i-гo слоя, м; – теплопроводность материала i-го слоя, Вт/(м·0С).Плотность теплового потока для многослойной стенки 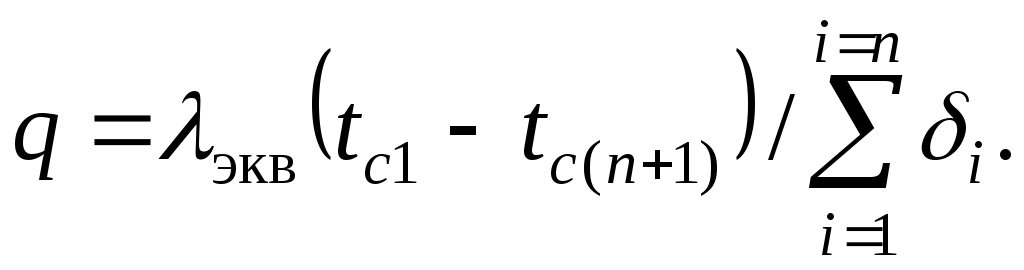 Стационарная теплопроводность цилиндрической стенки без внутренних источников теплоты. Температурное поле в однородной бесконечной стенке с наружным ивнутренним диаметрами соответственно  и  и   где и – температуры на внутренней и наружной поверхностях стенки; d – текущий диаметр цилиндрической поверхности, для которой определяется температура t.Температурное поле в стенке с учетом температурной зависимости теплопроводности 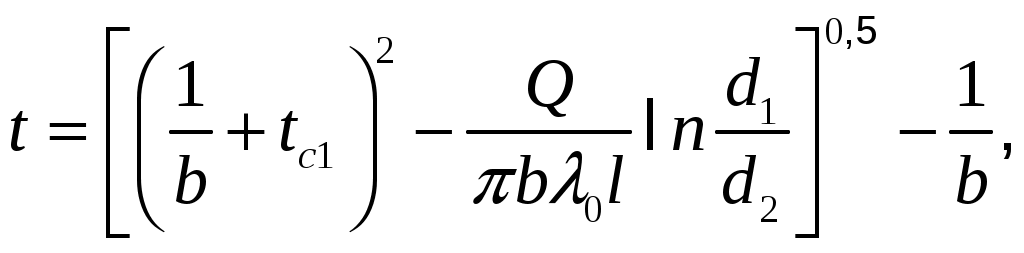  где  –длина цилиндрической стенки.Формула теплопроводностидля стенки, составленной из п цилиндрических слоев,  где и  – температуры на внутренней и внешней поверхностях многослойной стенки соответственно;  и  – внутренний и внешний диаметры 1-го слоя стенки.Температура на границе между i-м и (i+1)-·м плотно прилегающими слоями многослойной стенки  При расчете многослойных стенок используется эквивалентный коэффициент теплопроводности 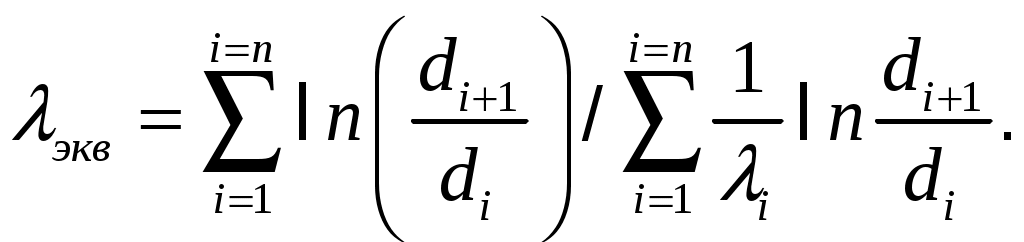 Стационарная теплопроводность плоской стенки с внутренними источниками теплоты. Для плоской пластины (λ=const), равномерно охлаждаемой с обеих сторон задана температура поверхности  .Одномерное температурное поле в пластине толщиной 2δ  где  .В формуле при х=0 температура в середине толщины пластины  Учитывая зависимость 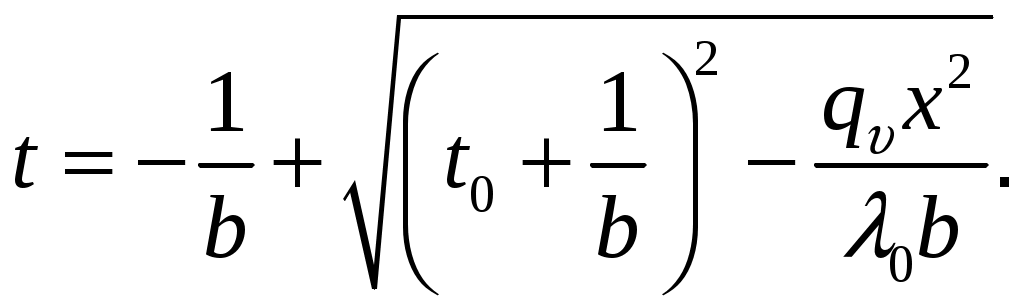 в условиях больших перепадов температур, температурное поле в пластине можно рассчитать по формуле Мощность внутренних источников теплоты для пластины определяется по формулам  .Связь между объемной  и поверхностной  плотностями тепловыделения используется при определении теплового потока на боковых поверхностях пластины Стационарная теплопроводность цилиндрического стержня с внутренними источниками теплоты. Для бесконечного стержня (λ=const) задана температура на оси  Температурное поле в стержне диаметром   где  .В формуле при  температура на поверхности стержня С учетом зависимости 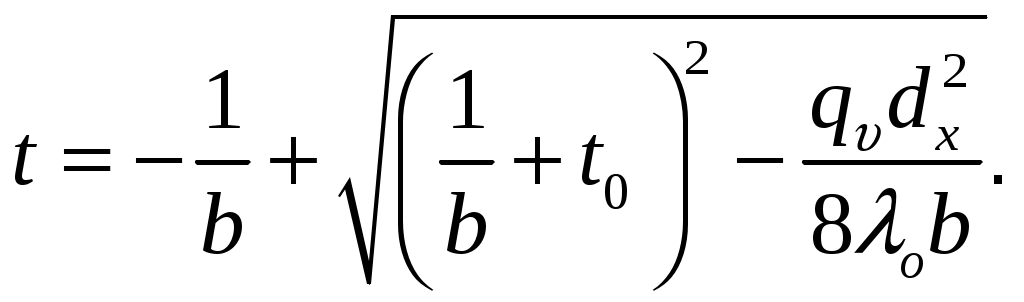 температурное поле в стержне Мощность внутренних источников теплоты для стержня  .Стационарная теплопроводность цилиндрической стенки с внутренними источниками теплоты. Теплота отводится через внешнюю поверхность трубы. Температурное поле в стенке трубы с внутренним радиусом 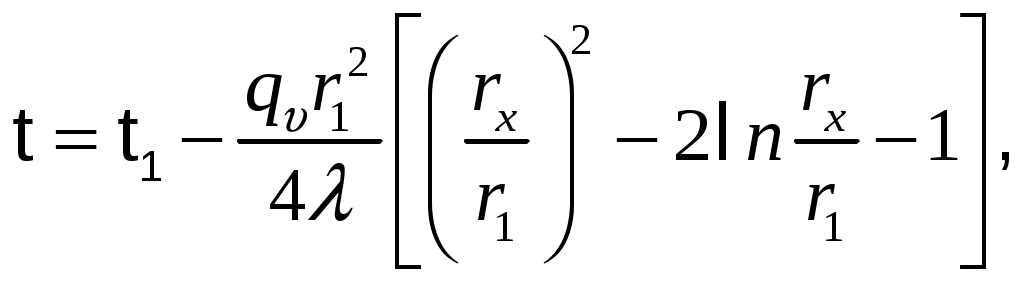 и внешним   где  , – температура на внутренней теплоизолированной поверхности трубы.Подставляя в формулу rx=r2, можно получить расчетное выражение для перепада температуры в стенке 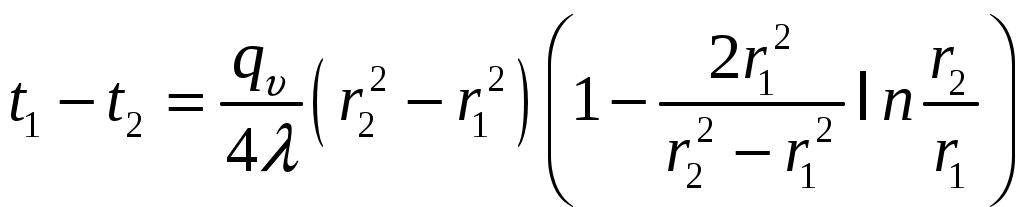 и формулу для линейной плотности теплового потока 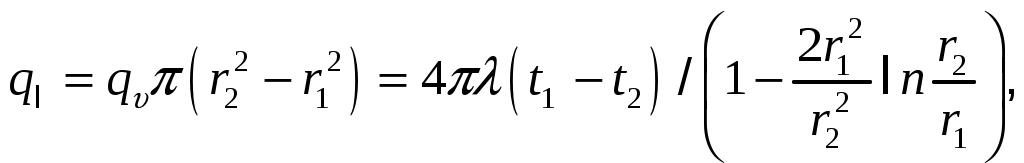 где  – температура на внешней поверхности трубы.Теплота отводится через внутреннююповерхность трубы. Температурное поле в стенке трубы 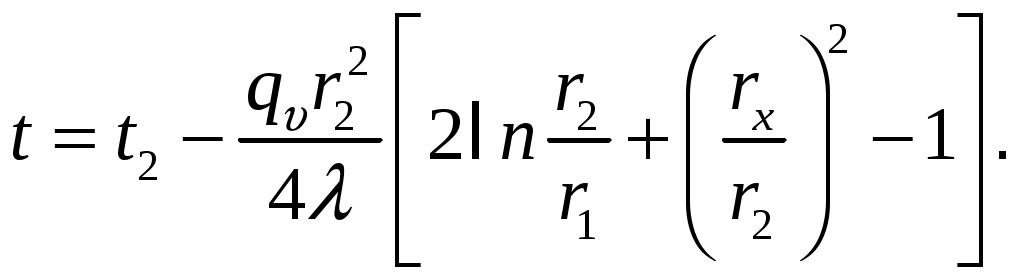 Перепад температур в стенке 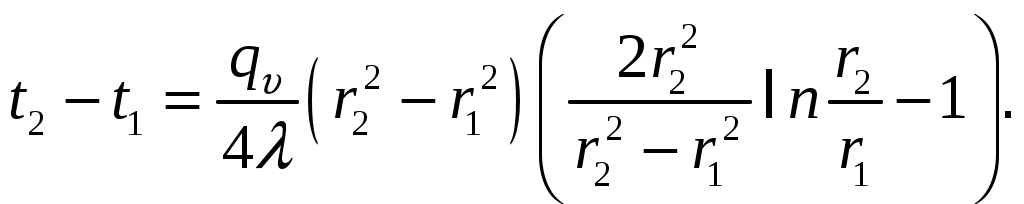 Линейная плотность теплового потока 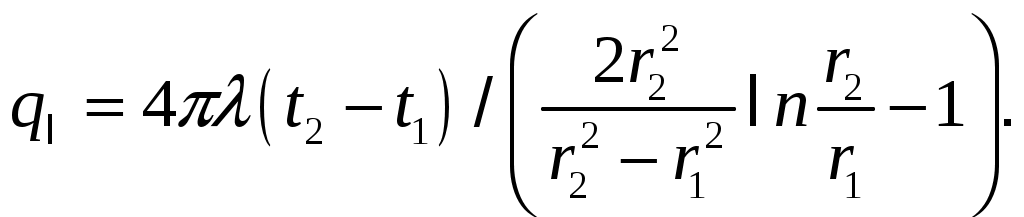 Теплота отводится через обе поверхности трубы. Перепад температур в стенке 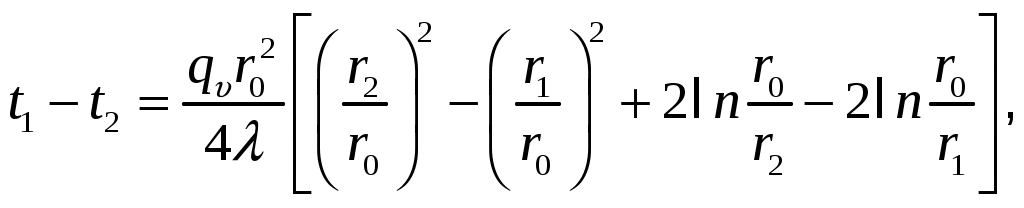 где  – радиус поверхности, которая имеет наибольшую температуру  Этот радиус определяется из зависимости  Наибольшую температуру в стенке трубы можно найти по выражению 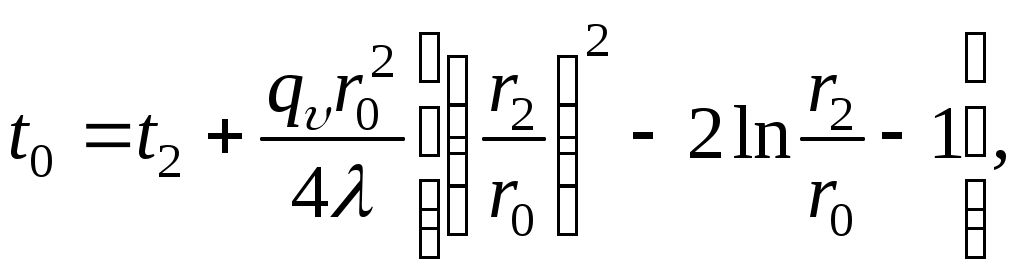 или 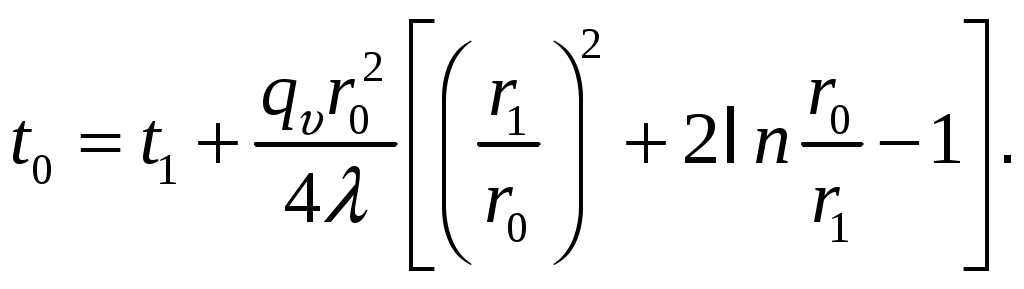 Тема 3. Теплопроводность при нестационарном режиме Охлаждение (нагрев) пластины, охлаждение (нагрев) бесконечно длинного цилиндра. Охлаждение (нагрев) шара. Определение количества теплоты, отданной (воспринятой) телом в процессе охлаждения (нагрева). Основные формулы для решения практических задач Теплопроводность пластины при нестационарном режиме. Пластина толщиной 2δ. Безразмерная температура пластины  где t –температура в пластине для момента времени т в точке с координатой х; t0 – температура пластины в начальный момент времени. Если  то температура на поверхности пластины (Х=1) температура на середине толщины пластины (Х=0)  температура внутри пластины на расстоянии х от ее средней плоскости  где  определяются по справочнику для пластины в зависимости от числа Bi.Температура  и  можно определить по графикам по известным числам Bi и Fo.Теплопроводность цилиндра при нестационарном режиме. Цилиндр радиусом  .Безразмерная температура цилиндра ,где t – искомая температура в цилиндре для радиуса  и времени  ,  .Если  , то температура на поверхности цилиндра   температура на оси цилиндра (R=0)  температура внутри цилиндра для радиуса rх  где  – определяются по справочнику для цилиндра в зависимости от числа Bi; I0(μ1rx/r0) – функция Бесселя первого рода нулевого порядка.Температуры  и  и можно определить по графикам по известным числам Bi и Fo.Количество теплоты  , Дж, отданной (воспринятой) телом за время τ в процессе охлаждения (нагревания), равно где  – количество теплоты, переданной за время полного охлаждения (нагревания), Дж;  – средняя по объему безразмерная температура тела в момент времени .Для пластинытолщиной  и площадью поверхности Fтеплота, переданная за время полного охлаждения, равна где m – масса пластины, кг; с – теплоемкость материала пластины, Дж/(кг·К);  – его плотность, кг/м3.Средняя по объему безразмерная температура пластины в момент времени τ при 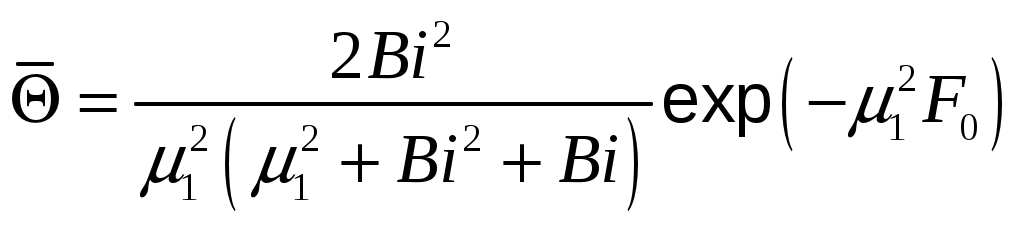 \Для цилиндрарадиусом  0 и длиной теплота, отданная за время полного охлаждения, равна Средняя по объему безразмерная температура цилиндра в момент времени 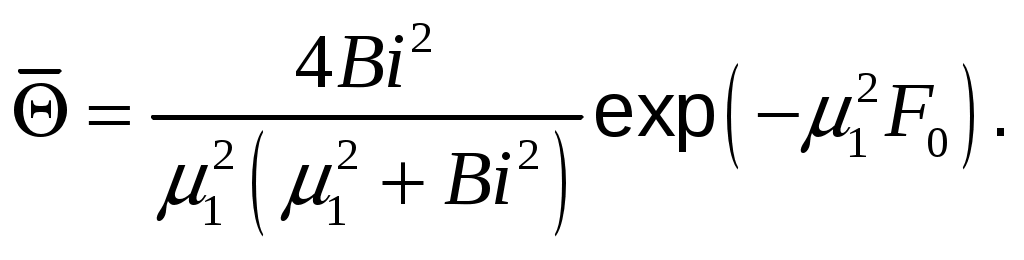при  равна |