Диплом до 1.06 2. Тепловой и конструктивный расчеты поршневого холодильного компрессора Классификация компрессоров
 Скачать 3 Mb. Скачать 3 Mb.
|
|
3.2. Расчет подшипника на грузоподъемность, шатуна, поршневого пальца, гильзы цилиндра На шатунные подшипники и шатунную шейку вала действуют переменные по величине и направлению в зависимости от угла поворота силы Рt и Рr`. Для определения характера нагружения подшипника, интенсивности неравномерного по окружности изнашивания шатунной шейки и выбора места подвода смазки строится полярная диаграмма сил, действующих на шатунную шейку коленчатого вала (рисунок 3.2). Результирующая сила, действующая на шатунный подшипник: 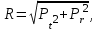  . .Значения результирующей силы приведены в таблице 3.3. Среднее давление на шатунную шейку: qср = Rср/ (dш·lв) = 1768,7/(0,06·0,025) = 1,18·106 Па, где dш = 0,06 – диаметр шейки, м; Rср = 1768,7 – среднее значение нагрузки определяем по развернутой полярной диаграмме, Н; lв = 0,025 – рабочая длина вкладыша, м. Таблица 3.3 – Результаты расчета результирующей силы, действующей на шатунный подшипник
Максимальное давление на шатунную шейку: qmax = Rmax/(dш·lв) = 8264/(0,06·0,025) = 5,5·106 Па, где Rmax = 8264 – максимальное значение нагрузки определяется по полярной диаграмме, Н; Для шатунных шеек вала допустимые значения: [qmax] = 6÷10 МПа; [qср] = 4÷6 МПа. С помощью полярной диаграммы сил, действующих на шатунную шейку, строится условная диаграмма изнашивания (рис. 3.2), считая, что износ пропорционален нагрузке и распространяется равномерно на дуге 120 ± 7,5˚ (по 60˚ в каждую сторону от точки приложения вектора равнодействующей силы к шейке вала). Результаты расчета суммарной нагрузки на шатунную шейку приведены в таблице 3.3. 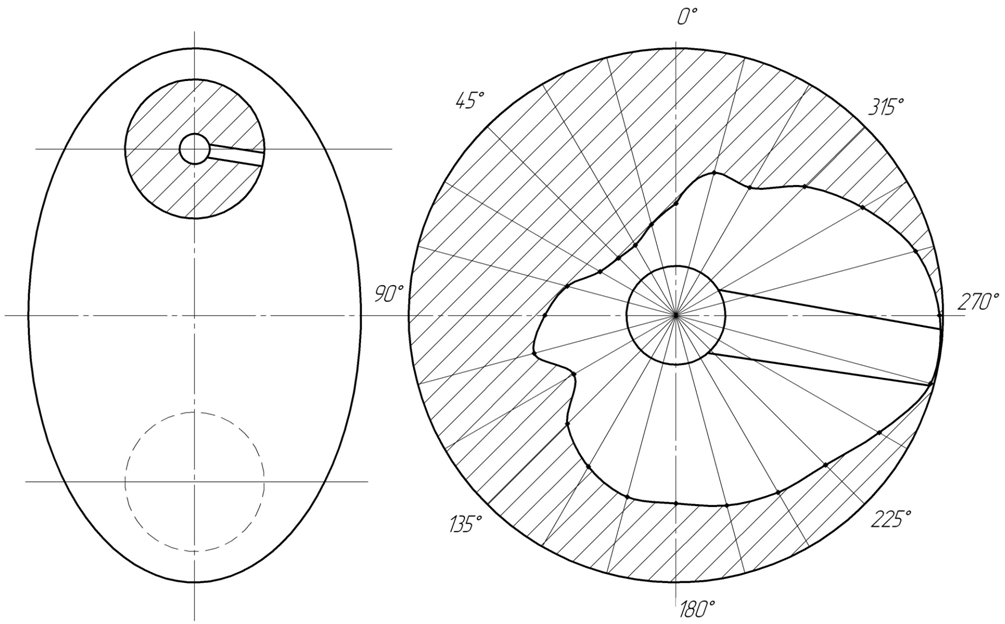 Рис. 3.2 – Условная диаграмма изнашивания 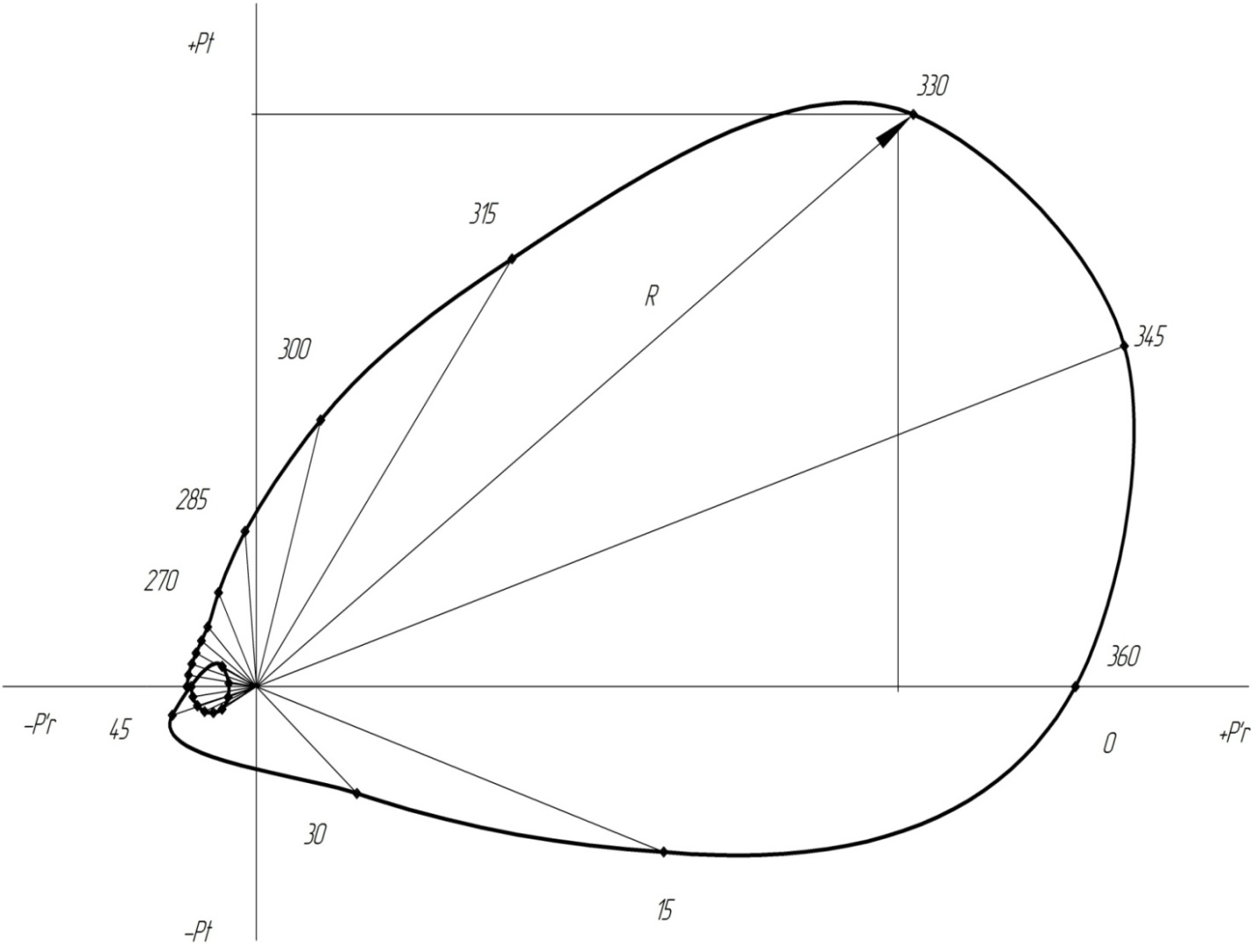 Рис. 3.3 – Полярная диаграмма Расчет подшипника заключается в определении требуемой динамической грузоподъемности подшипника исходя из требуемой долговечности при эквивалентной динамической нагрузки: Р = (Х∙V∙Fr + Y∙Fa)∙κд∙κт, где Х = 1 – коэффициент радиальной нагрузки; V = 1 – коэффициент вращения; Fr = 1200 – радиальная нагрузка, Н; Y = 1,78 – коэффициент осевой нагрузки; Fa – осевая нагрузка: Fa = π∙dпр2∙(ро – рр)/4 = 3,14∙0,0352∙(0,2 – 0,1)/4 = 96 Н, где dпр = 0,035 – диаметра приводного конца вала, м; ро = 0,2 – давление кипения, МПа; рр = 0,1 – наружное давление, МПа; κд = 2,5 – коэффициент безопасности, учитывающий влияние динамических условий работы; κт = 1 – температурный коэффициент. Р =(1∙1∙1200 + 1,78∙96)∙2,5∙1 = 1374 Н. 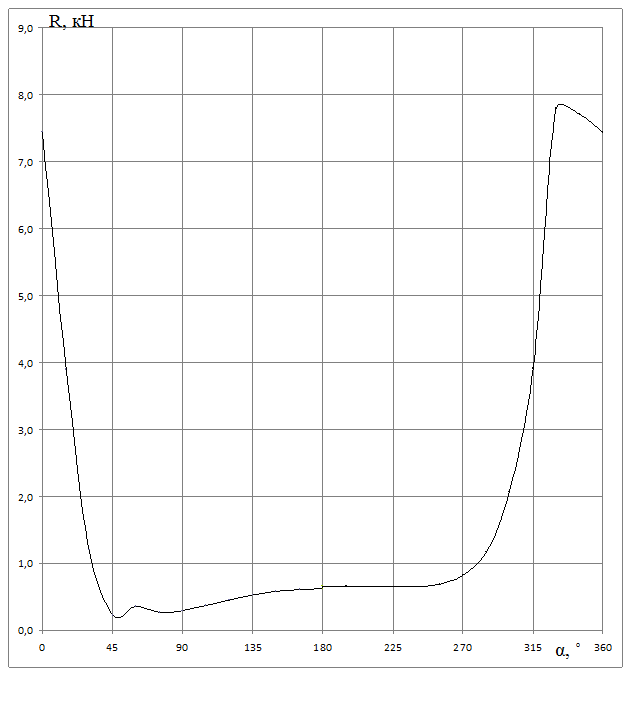 Рис. 3.4 – Развернутая полярная диаграмма Рис. 3.4 – Развернутая полярная диаграммаТребуемая грузоподъемность подшипника: с = [Lh∙60∙n/(a23∙106)]1/p∙P = [40000∙60∙24.(0.4∙106)]1/0,3∙1374= 20667 H, где n = 24 с-1 – частота вращения; a23 = 0,4 – коэффициент ,характеризующий совместное влияние качества металла и условий эксплуатации подшипника; р = 0,3 – показатель степени. Выбираем подшипник № 1210 ГОСТ 28428-90. Прочность стержня шатуна проверяется по среднему и минимальному сечениям. Напряжение растяжения в среднем сечении: σр = Pш/fср = 161,29/(5,84·10-4) = 0,28·106 Па, где Pш = 161,29 – наибольшая растягивающая сила, действующая на шатун, Н; fср = 5,84·10-4 – площадь среднего сечения, м2. Суммарные напряжения от сжатия и продольного изгиба в среднем сечении: В плоскости сечения шатуна: σсx = Pшс∙(1/fср + 0,000526∙l/Ix) = = 8507,87·(1/(584·10-4) + 0,000526·0,174/(0,02·10-6)) = 53,5·106 Па. где Рш.с. = 8507,87 – наибольшая сжимающая сила, действующая на шатун, Н; Ix – момент инерции среднего сечения шатуна относительно оси х-х: Ix = 2∙{b1∙h23/12 + b1∙h2 [(h1–h2)/2]2} + b2∙(h1– 2∙h2)3/12 = = 2·{0,023·0,00743/12 + 0,023·0,0074·[(0,03 – 0,0074)/2]2} + + 0,014·(0,03 – 2·0,0074)3/12 = 0,02·10-6 м4, где b1 = 0,023 м; h2 = 0,0074 м; h1 = 0,03 м; b2 = 0,014 м. 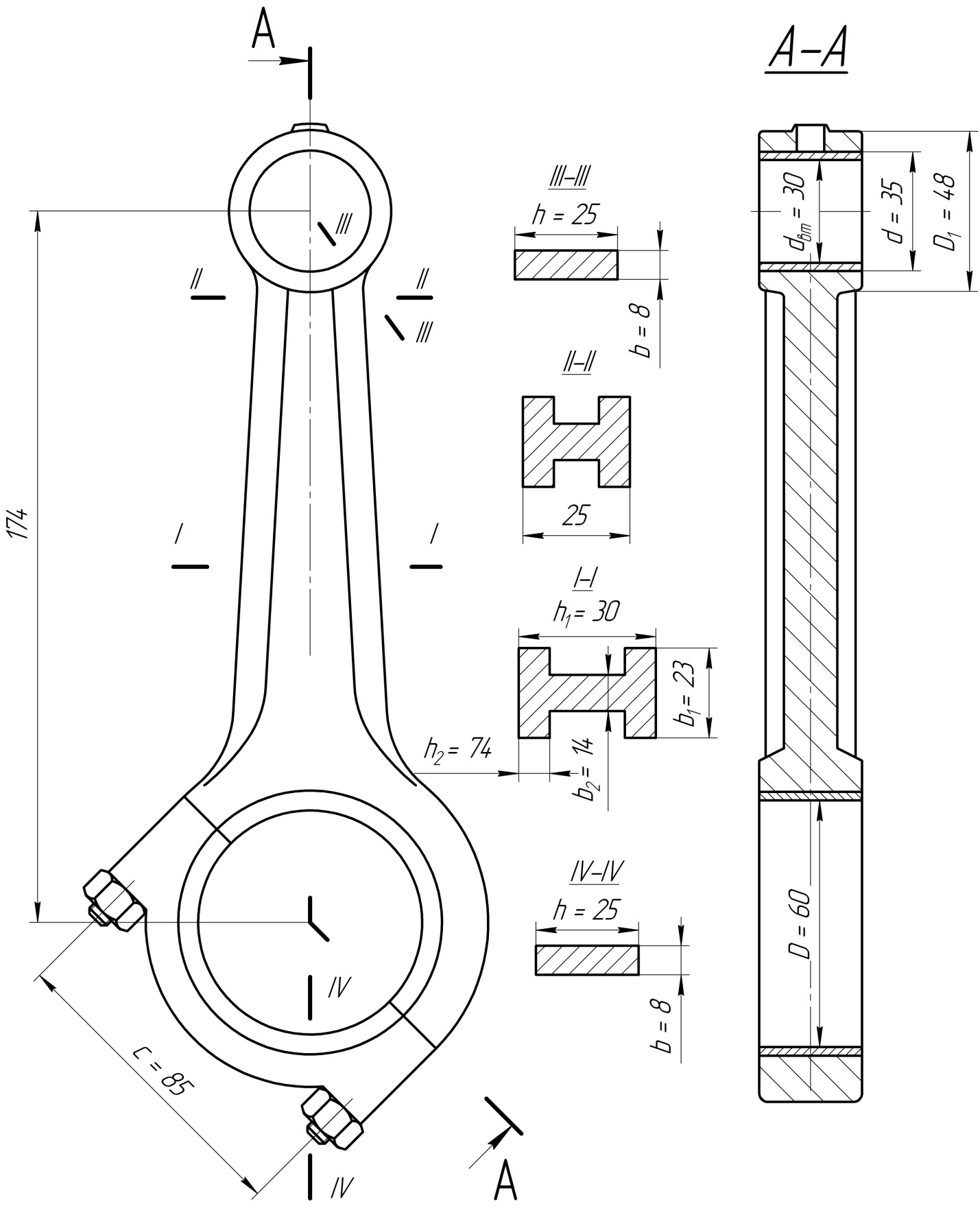 Рис. 3.5 – Схема и основные размеры шатуна. В перпендикулярной плоскости: σсy = Pшс∙(1/fср + 0,000132∙l1/Iy) = = 8507,87·(1/(5,84·10-4) + 0,000132·0,13/(0,0027·10-6)) = 69·106 Па, где l1 – длина стержня шатуна, м; l1= l – (D + d)/2 = 0,174– (0,06 + 0,03)/2 = 0,13 м, где D = 0,06 м; d = 0,03 м; Iy – момент инерции среднего сечения шатуна относительно оси y-y; Iy = [2∙h2∙b13 + (h1 – 2∙h2)∙b23]/12 = = [2·0,0074·0,0233 + (0,03 – 2·0,0074)·0,0143]/12 = 0,0027·10-6 м4. Напряжение сжатия в минимальном сечении: σс = Рш.с./fmin = 8507,87/(4,97·10-4) = 17,1·106 Па, где fmin = 4,97·10-4 – площадь минимального сечения, м2; Допускаемые напряжения для шатунов из углеродистой стали 100 МПа. Запас прочности стержня шатуна на выносливость: n = (σ-1)p/(kσ∙σa/εσ + ψσ∙σm), где (σ-1)p ≈ 0,31σв – предел выносливости материала при симметричном цикле растяжение-сжатие, Па; σв – временное сопротивление материала шатуна, Па; kσ – коэффициент концентрации напряжений (kσ =1 при обработанных поверхностях, kσ = 1,3÷1,35 при необработанных поверхностях); εσ = 0,81 – коэффициент влияния абсолютных размеров сечения, определенный по наибольшему размеру рассчитываемого сечения; ψσ = 0,05÷0,2 – коэффициент, характеризующий чувствительность материала к асимметрии цикла Для плоскости х-х: σах = (σр – σсх)/2 = (0,28 + 53,5)·106/2 = 26,89·106 Па. σmx = (σр+σсх)/2 = (0,28 – 53,5)·106/2 = –26,61·106 Па. Для плоскости y-y: σау = (σр– σсу) / 2 = (0,28 + 69)·106/2 = 34,64·106 Па. σmу = (σр + σсу) / 2 = (0,28–69)·106/2 = –34,36·106 Па. Запас прочности: nx = 190·106/(1,3·26,89·106/0,8 – 0,2·26,61·106) = 4. nу = 190·106/(1,3·34,64·106/0,8 – 0,2·34,36·106) = 3,4. Допускаемый запас прочности: 2÷4. На поршневую головку действуют переменная по величине и направлению сила Pш и постоянное давление со стороны втулки. Когда шатун растянут, нагрузка на головку почти равномерно распространяется по верхней половине, а когда шатун сжат, то по нижней половине примерно по косинусоидальному закону. В том и другом случаях опасное сечение находится в месте перехода стержня в головку. Напряжение в этом сечении от действия силы Pш: σ = Nа/S + Mа/W, где Nα – нормальная сила, Н; Mα – изгибающий момент, Н·м; W – момент сопротивления сечения, м3; При растяжении: Nа/Pш.р = 0,382; Mа/ Pш.р∙ρ = 0,081; Pш.р. = 161,19 Н; ρ = (D1 + d)/4 = (0,048 + 0,03)/4 = 0,02 м; Na = 0,382·161,19 = 61,6 Н. Mа = 0,081·161,19·0,02 = 0,26 Н·м. S = b∙h, где b = 0,025м; h = (D – b)/2 = (0,048 – 0,025)/2 = 0,01 м; S = 0,025·0,01 = 2,5·10-4 м2; W = b∙h2/6 = 0,025·0,012 / 6 = 0,4·10-6 м2; σр = 61,6/(2,5·10-4) + 0,26/(0,4·10-6) = 1,9·106. При сжатии: σс = 340,3/S + Mа/W = 340,3/(2,5·10-4) + 5,1/(0,4·10-6) = 14,1·106 Па, где Nа/Pш.р = 0,4; Mа/ Pш.р∙ρ = 0,03; где Рш.с. = 8507,87 Н; Na = 0,04·8507,87 = 340,3 Н; Mа = 0,03·8507,87·0,02 = 5,1 Н·м. Напряжение от давления со стороны втулки: σ = p·d = 24·106·0,03/(2·0,01) = 36·106 Па, где p – давление между головкой и втулкой; 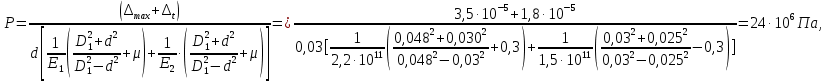 где Δmax = 3,5∙10–5 – максимальный натяг между втулкой и головкой, м, Δt = (αвт – αг)∙d∙t = (1,7 – 1,1)·10-5·0,03·100 = 1,8·10-5м – разница теплового расширения втулки и головки, где αвт, αг – коэффициенты теплового расширения втулки (бронза) и головки (сталь), t ≈ 100°C – температура нагрева сопряжения, E1, E2 – модули упругости материала втулки и головки, Μ = 0,3 – коэффициент Пуассона. Головка нагружена ассиметричным циклом напряжений с амплитудой средним напряжением: σа = (σр – σс)/2 = (1,9 + 14)·106/2 = 7,95·106 Па. σm = (σр + σс)/2 + σ = (1,9–14)·106/2 + 36·106 = 29,95·106 Па. Запас прочности головки на выносливость: n = 190·106/(1,3·7,95·106/0,81 – 0,2·29,95·106) = 6,7. На кривошипную головку шатуна действует сила: Рр = Pш.р. + I'ш.вр. =161,19 + 316,4 = 478 Н, где Pш.р = 161,19 – наибольшая растягивающая шатун сила при работе компрессора на холостом ходу, Н; I'ш.вр. = 316,4 – сила инерции вращающейся части шатуна, расположенной до разъема кривошипной головки (без учета массы крышки кривошипной головки шатуна), Н. Условно считается, что крышка жестко связана с телом шатуна. Опасным считается сечение IV−IV (рисунок 3.5). Напряжение от силы Рр в этом сечении: y = No/S + Mo/W , где No/Рр = 0,39; Mo/Рр·c = 0,056; Nо – нормальная сила; Nо = 0,39·161,19 = 62,9 Н; Ma – нормальная сила; Ma = 0,056·478·0,085/2 = 1,13 Н·м. S = b·h, где b = 0,008 м, h = 0,025 м, S = 0,008·0,025 = 2·10-4 м2, W – момент сопротивления сечения: W = b·h2/6 = 0,008·0,0252/6 = 0,8·10-6 м2. y = 62,9/(2·10-4) + 1,13/0,8·10-6 = 1,7·106 Па. Допускаемые напряжения в крышке из стали 40 [σ] = 200 МПа. Днище тронкового поршня рассчитывается как круглая пластина, заделанная по контуру (рис.11.). Наибольшие напряжения в днище (в месте заделки): σr = − 0,75·Δр·r22/h2= − 0,75·1,93·106·0,01352/0,0082 = −4,1·106 Па, где Δр = 1,93·106 – наибольшая разность давлений, воспринимаемых днищем, Па; r2 = 0,0135 – радиус контура заделки, м; h = 0,008 – толщина днища, м; σt = μ·σr = 0,26·(− 4,1·106) = −1,1·106 Па, где μ = 0,26 − коэффициент Пуассона для материала поршня. σz = −pн = −0,9·106 Па, где pн= 0,9·106 – максимальное давление нагнетания для R134а, при Тк = 308К, Па. Эквивалентное напряжение в алюминиевом поршне по энергетической теории прочности: σ = (0,5·[(σr – σt)2+(σt – σz)2 + (σz – σr)2])1/2 = = (0,5·[(–4,1 + 1,1)2 + (–1,1 + 0,9)2 + (–0,9 + 4,1)2])1/2 = 3,1·106Па. Допускается для днища алюминиевых поршней [σ*] = 30 МПа. Давление на боковую стенку поршня: q = pн/(D·H) = 638/(0,078·0,084) = 0,097·106 Па, где рн = Рmax·tgβ = 8507,87·0,075 = 638 Н. D = 0,078 – диаметр поршня, м; H = 0,084 – высота поршня без высоты поршневых и маслосъемных колец м; Давление на боковую стенку не должно превышать q = 0,15·106÷0,35·106 МПа. 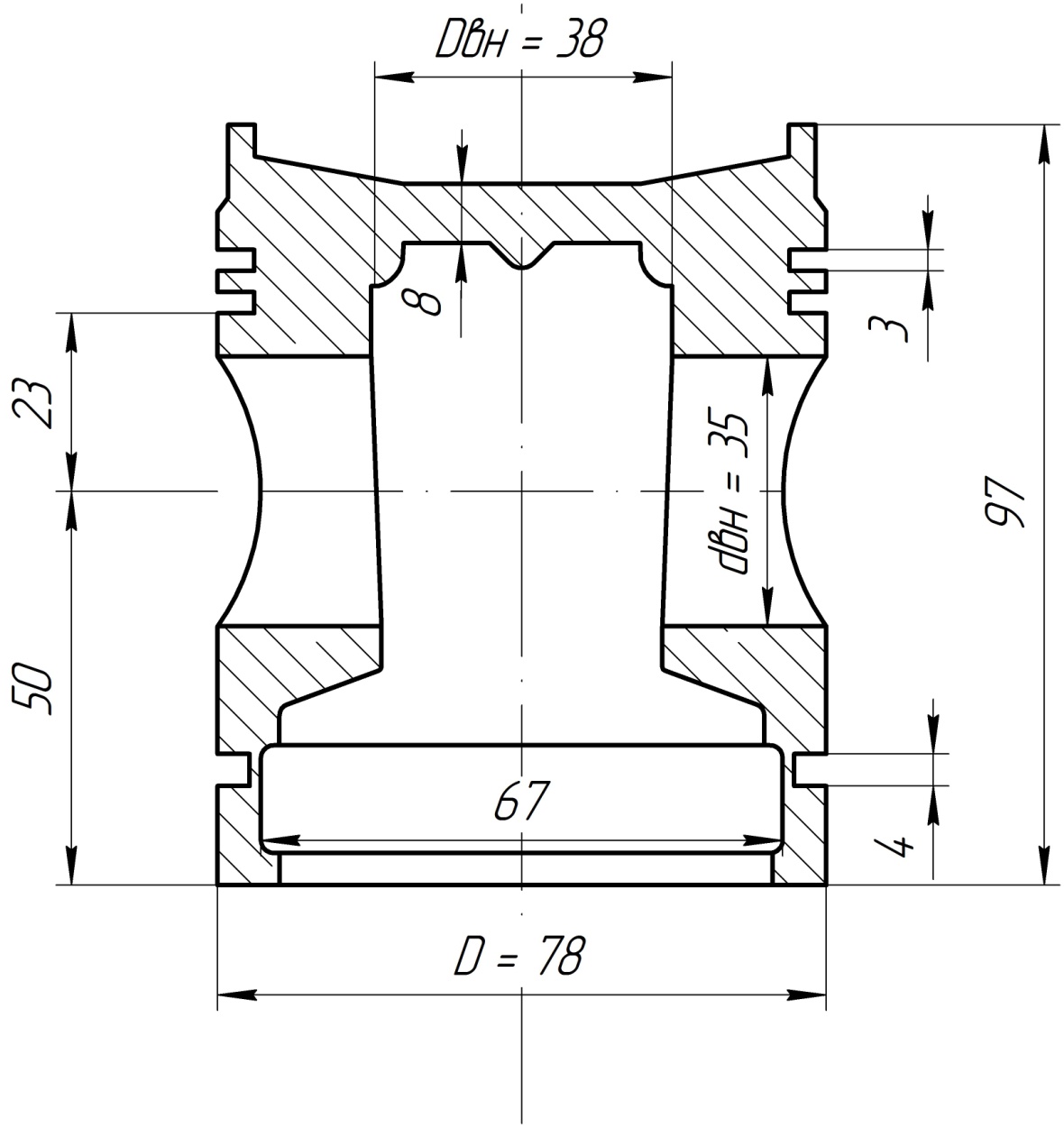 Рис. 3.6 – Поршень компрессора Наибольшее давление на поршневой палец в подшипнике: qmax = Pш/(d·a) = 8507,87/(0,035·0,033) = 7,4·106 Па, где Рш = Рш.с .= 8507,87 – наибольшая по абсолютному значению сила, действующая на шатун, Н; d = 0,035 – наружный диаметр пальца (рис. 3.7), м; а = 0,033 – длина подшипника (рис. 3.7), м; Давление на поршневой палец в подшипнике не должно превышать qmax = 15 ÷ 20 МПа. Наибольшее давление в месте соединения пальца с поршнем: q'max = Pш/(2·d·b) = 8507,87/(2·0,035·0,007) =17,4·106 Па, где b = 0,007 – длина поверхности пальца в месте посадки, м.  Рис. 3.7 – Расчетная схема поршневого пальца Для алюминия давление в месте соединения пальца с поршнем не должно превышать q'max = 25 ÷ 35 МПа. Напряжение от изгиба: σи = Pш·(l + 2·c − 1,5·а)/[1,2·(1 − α4)·d3] = = 8507,87·(0,053 + 2·0,039 − 1,5·0,033)/[1,2·(1 − 0,574)·0,0353] = 103·106 Па, где l= 0,053 – длина пальца (рис. 3.7), м; с = 0,039 м – расстояние между местами посадки пальца в поршне; α = 0,57− отношение внутреннего диаметра пальца к наружному. Для углеродистых сталей напряжение от изгиба не должно превышать [σи] = 120 МПа. Напряжение на срез в сечении между бобышкой поршня и головкой шатуна: τ = 0,85·Рш·(1 + α + α2)/[d2·(1 − α4)] = =0,85·8507,87·(1 + 0,57 + 0,572)/[0,0352·(1 − 0,574)] = 12,5·106 Па. Напряжение на срез в сечении между бобышкой поршня и головкой шатуна не должно превышать τ = 100 МПа. Гильзу цилиндра рассчитывают на пробное гидравлическое давление p= 3,5 МПа. Нормальные напряжения в стенке гильзы: σt = p·(r12 + r22)/(r22−r12) = = 3,5·106·(0,0352 + 0,042) / (0,042 − 0,0352) = 26,4·106 Па, где r1 = 0,035 – радиус внутренней окружности сечения гильзы, м; r2 = 0,04 – радиус наружной окружности сечения гильзы, м. σr = − p = −3,5·106 Па. Эквивалентное напряжение: σэкв= σt – υ·σr = (26,4 + 0,3·3,5)·106 = 27,5·106 Па, где υ = 0,3 − отношение предела прочности на растяжение к пределу прочности на сжатие для чугуна. Значение эквивалентных напряжений для чугуна не должны превышать [σэкв] = 20÷35 МПа. 3.3. Конденсатор водяной горизонтальный кожухотрубный Температура охлаждающей воды на входе в конденсатор: tw1 = tк – Δtк= 35 – 8 = 27°C, где Δtк = 8°C – конечная разность температур в процессе теплообмена. Температура охлаждающей воды на выходе из конденсатора: tw2 = tw1 + Δtw= 27 + 5 = 32°C, где Δtw = 5°C – разность температур входящей и выходящей из конденсатора воды. Тепловой поток конденсатора: Qк = Ga∙(i2 – i3) = 0,124·(457 – 249) = 25,79 кВт. Средняя логарифмическая разность температур в аппарате: 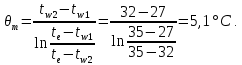 Массовый расход воды через конденсатор: Gw = Qк/(cw∙Δtw) = 25,79/(4,174∙5) = 1,24 кг/с, где сw = 4,174 – теплоемкость воды при twср, кДж/(кг·К). Средняя температура воды в конденсаторе: 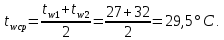 В качестве поверхности теплопередачи – шахматный пучок из медных труб со стандартным наружным оребрением. Параметры трубы фреонового конденсатора:
Скорость воды в аппарате принимается w = 1,1 м/с; Число труб в одном ходе: n1 = 4∙Gw/(π∙ρw∙dвн2∙ωw) = 4∙1,24/(3,14∙995,8∙0,01152∙1,1) = 11, где ρw= 995,8 – плотность воды при twср. = 29,5°C, кг/м3. Значение числа труб в одном ходе округляется до ближайшего целого числа, тогда n1 = 11. Уточняется скорость воды в аппарате: ωw = 4∙Gw/(π∙ρw∙dвн2∙n1) = 4∙1,24/(3,14∙995,8∙0,01152∙11) = 1,1 м/с. Число Рейнольдса: Re = (ωw∙dвн)/νw = (1,1∙0,0115)/0,815106 = 15521, где w = 0,815106 – кинематическая вязкость воды при twср =29,5С, м3/с; Число Нуссельта: Nu = 0,021·Re0,8·Pr0,43·пер = 0,021155210,8 5,53,431 = 98,7, где Pr = 5,53 – число Прандтля при twср =29,5С; пер – коэффициент для переходного режима (т.к. Re = 15380 > 10000 – турбулентный режим течения и пер = 1. Nu. Коэффициент теплоотдачи со стороны воды: αw = Nu∙λw/dвн = 98,7∙0,607/0,0115 = 5173 Вт/(м2К), где w = 0,607 теплопроводность воды при tw ср = 29,5С, Вт/(мК). Плотность теплового потока со стороны воды: 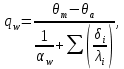 где 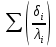 = 2,6103 суммарное термическое сопротивление стенки трубы и загрязнений для R134а, (м2К)/Вт. = 2,6103 суммарное термическое сопротивление стенки трубы и загрязнений для R134а, (м2К)/Вт.Для дальнейших расчетов необходимо найти плотность теплового потока qвн. Точное значение qвн на данном этапе расчета установить невозможно, поэтому вычисляется ориентировочное значение q´, где предполагается, что а = 0,3m = 0,35,1 = 1,53С, тогда 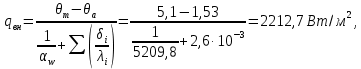 Число труб, расположенных по большой диагонали внешнего шестиугольника: m= 0,75∙(Qк/q´∙S∙dвн∙l/d)1/2 = = 0,75∙( 25790/7899∙0,02145∙0,0115∙6)1/2 = 9,7, где q´= 2112,7∙0,7∙5,1 = 7899 Вт/м2; S – горизонтальный шаг труб; S = 1,3∙dн = 1,30,0165 = 0,02145 м. Округляется значение числа т до ближайшего нечетного числа т = 11. Коэффициент теплоотдачи со стороны холодильного агента: αs = 0,72∙((i2 – i3)∙ρ2∙λ3∙g/μ∙d0)1/4∙(m/2)-0,167∙θ-0,25∙β∙ψр = = 0,72∙((457 – 249)∙1169,552∙0,080053∙9,81/1,135∙0,0165)1/4∙× ×(11/2)-0,167∙θ -0,25∙4∙1,599 = 18148∙θ-0,25, где ρ = 1169,55 – плотность агента R134а при tк = 35°C, кг/см3; λ = 0,08005 – теплопроводность агента R134а при tк = 35°C, Вт/(мК); μ = 1,135∙10-4 – динамическая вязкость агента R134а при tк = 35°C, Пас; р коэффициент, учитывающий различные условия конденсации на горизонтальных и вертикальных участках поверхности трубы: 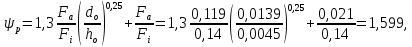 где Fв площадь поверхности вертикальных участков ребер длиной 1 м: 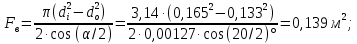 Fг – площадь поверхности горизонтальных участков трубы длиной 1 м: Fг = Fн Fв = 0,14 – 0,119 = 0,021 м2; hр – приведенная высота ребер: 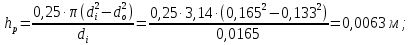 Плотность теплового потока со стороны холодильного агента: qа = αа ·θа-0,25·θа = 18148∙θ-0,75. Плотность теплового потока со стороны воды: qw = (θm–θa)/(1/αw) + ∑(δi/λi) = (5,1–θa)/(1/5173) + 0,26·103 = 2206·(5,1 – θa). Система двух уравнений: qw = (5,1 – θa)/(1/5173) + 0,26·103 = 2206·(5,1 – θa); qа = αа·θа-0,25·θа = 18148∙θ-0,75. С помощью графоаналитического метода определяется внутренняя плотность теплового потока в установившемся режиме работы аппарата, при котором выполняется условие: qw = qа = qвн. Таблица 3.4 – Результаты расчета значений q для ряда значений а
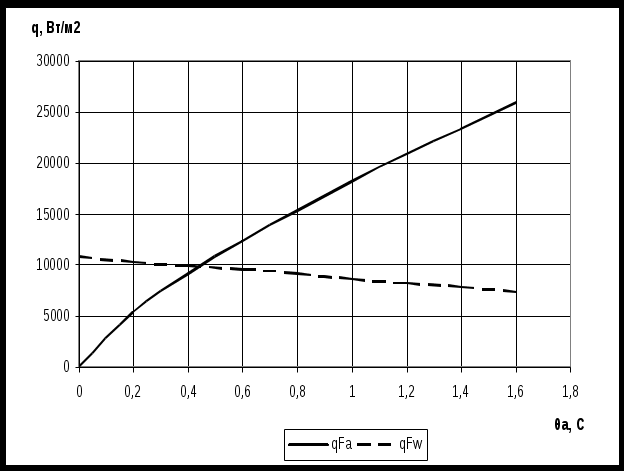 Рис. 3.8 – График пересечения qw и qа По этим данным на рисунке 3.8 приведены зависимости от а тепловых потоков со стороны воды и хладагента. Точка пересечения кривых определяет значение qвн = 9800 Вт/м2. Площадь внутренней поверхности теплопередачи: Fвн = Qк /qвн = 25790/9800 = 2,6 м2. Площадь наружной поверхности теплопередачи: Fн = Fвн = 2,64 = 10,4 м2. Общее число труб в аппарате: n =0,75∙m2 + 0,25 =0,75∙112 + 0,25 = 91. Число ходов в аппарате по воде: z = n/ n1 = 91/11 = 8. Принимаем z = 8, тогда n = n1∙z= 11∙8 = 88. Диаметр трубной решетки: D = m∙s =1∙0,02145 = 0,2 м. Длина одной трубы в аппарате: l = Fвн/(π∙dвн∙n) = 2,6/(3,14∙0,0115∙88) = 0,8 м. Δр = {0,042∙εш/[(ω∙dвн)0,25∙(tw + 40)0,35]∙(l/dвн) + 1,75}∙(z∙ωw2∙ρw/2) = = {0,042∙1/[(1,1∙0,0115)0,25∙(29,5+40)0,35]∙(0,8/0,0115)+1,75}∙(8∙1,12∙995,8/2) = = 0,041 МПа, где εш – коэффициент, учитывающий влияние шероховатости поверхности труб. Для медных труб εш = 1. 3.4. Испаритель горизонтальный кожухотрубный затопленного типа Испаритель горизонтальный кожухотрубный затопленного типа. Температура рассола на выходе из испарителя: ts2 = t0 +Δts = 10 + 3 = 7С, где Δt = 3С – конечная разность температур в процессе теплообмена; Температура рассола на входе в испаритель: ts1 = ts2 + Δts = –7 + 5 = 2С, где Δts= 5С – разность температур входящего и выходящего из испарителя рассола; Логарифмическая разность температур в испарителе:  Температура замерзания рассола: tзам = t0 10 = 10 10 = 20С. Выбирается рассол СаСl2 со следующими свойствами:
В качестве поверхности теплопередачи выбирается шахматный пучок из медных труб со стандартным наружным оребрением. Параметры трубы фреонового испарителя такие же, как и у фреонового конденсатора. Скорость рассола в аппарате принимается s = 1,1 м/с. Число труб в одном ходе: 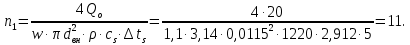 Принимается n1 = 11, тогда действительная скорость рассола: 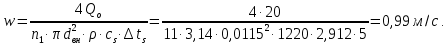 Число Рейнольдса: Re = (ωw∙dвн)/νw = (0,99∙0,0115)/3,58106 = 3180, где w = 3,58106 – кинематическая вязкость рассола при tsср = –4,5С, м3/с. Число Нуссельта: Nuж = 0,021Reж0,8Pr0,43пер = 0,0213180 0,824,07,430,57 = 29,8, где пер = 0,57 – коэффициент для переходного режима при Reж = 3180. Коэффициент теплоотдачи со стороны рассола, отнесенный к внутренней поверхности трубы: 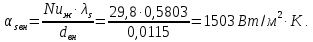 Плотность теплового потока со стороны рассола: 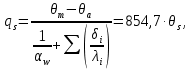 где 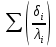 = 0,5103 суммарное термическое сопротивление стенки трубы и загрязнений для рассола, (м2К)/Вт. = 0,5103 суммарное термическое сопротивление стенки трубы и загрязнений для рассола, (м2К)/Вт.Плотность теплового потока со стороны рабочего вещества, отнесенная к внутренней поверхности трубы: qFа = 580·p00,45·пр1,82·θа1,82β = 5802,451θа1,82·4 = 3169θа1,82, где pо = 2 – давление кипения при tо = 10С, бар; пр =1 – коэффициент, учитывающий влияние числа рядов труб по высоте пучка. Получены уравнения для определения плотности теплового потока: 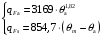 С помощью графоаналитического метода определяется внутренняя плотность теплового потока в установившемся режиме работы аппарата, при котором выполняется условие: qFs = qFa= qFвн. Таблица 3.5 – Результаты расчета значений q для ряда значений а
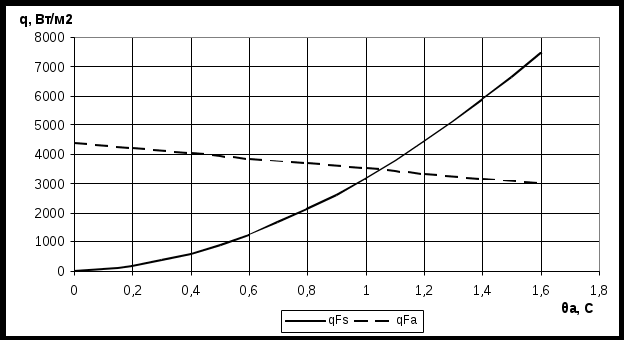 Рис. 3.9 – График пересечения qs и qа По этим данным приведены зависимости от а тепловых потоков со стороны рассола и хладагента (рисунок 3.9). Точка пересечения кривых определяет значение qFвн = 3400 Вт/м2. Площадь внутренней теплопередающей поверхности: Fвн = Q0/qFвн =20000/3400 = 5,9 м2. Площадь наружной поверхности теплопередачи: Fн = Fвн = 5,94 = 23,6 м2. Принятое размещение труб на трубной решетке – по периметрам правильных шестиугольников. Шаг труб: S = 1,3∙dн = 1,3∙0,0165= 0,0215 м. Число труб, размещаемых по диагонали внешнего шестиугольника: m= 0,75∙(Fвн /dвн∙S∙κ)1/3= 0,75∙(5,9 /0.0115∙0,0215∙7)1/3 = 13, где κ= 5 – 7 – отношение длины труб в аппарате к его диаметру. Внутренний диаметр обечайки: Dвн = m∙s = 13∙0,0215 = 0,280 м. Длина труб в пучке: l = D∙κ = 0,280∙7 = 1,96 м. Принимаем l= 2 м. Тогда общее количество труб в пучке: n = Fвн/π∙dвн∙l = 5,9 /3,14∙0,0115∙2) = 85. Число заходов: z = n/n1 = 85/13 = 6. |
