Термодинамика химических равновесий и сольватации реагентов в растворах
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
Расчетная работа №1 ТЕМА: ТЕРМОДИНАМИКА ХИМИЧЕСКИХ РАВНОВЕСИЙ И СОЛЬВАТАЦИИ РЕАГЕНТОВ В РАСТВОРАХ ЦЕЛЬ: 1. Освоить физико-химический метод анализа влияния водно-органических растворителей на силу слабых электролитов и устойчивость коронатов. 2. Выполнить статистический анализ физико-химических данных. 3. Рассчитать термодинамические характеристики химических равновесий диссоциации и комплексообразования. 1 МЕТОДОЛОГИЧЕСКАЯ ЧАСТЬ Взаимосвязь между константами химических равновесий (комплексообразования, диссоциации, ионной ассоциации) и энергиями Гиббса переноса реагентов 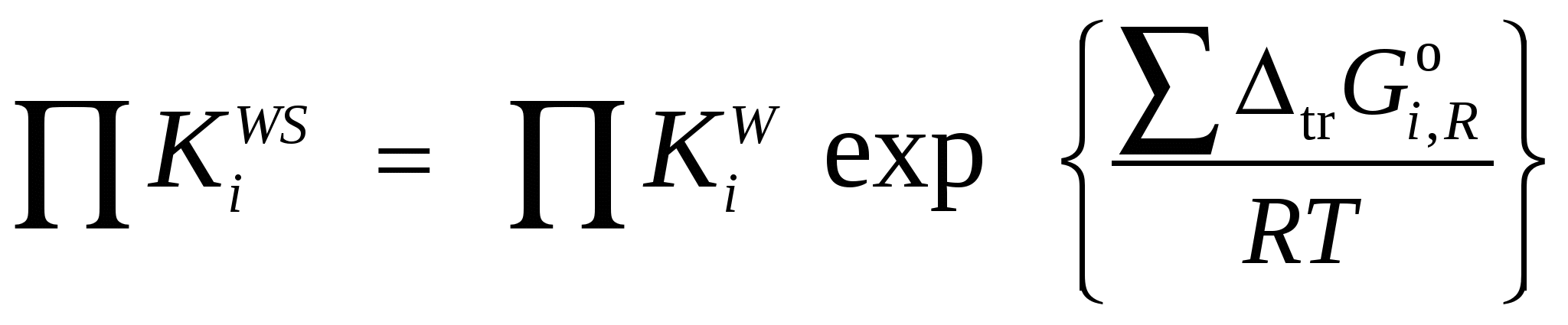 (1) (1)Здесь ПKi = K-1i,asKi,HAKi,ML; Ki,as – константа ионной ассоциации соли; Ki,HA – константа диссоциации лиганда; Ki,ML – константа реакции образования комплексов катионов с электронодонорными лигандами. Для частного случая диссоциации одноосновной карбоновой кислоты общее уравнение (1) преобразуется в уравнение Измайлова Н.А.: Для частного случая образования монолигандных комплексов катионов с краун-эфирами (коронатов) M+ +L ML+ общее уравнение (1) преобразуется в уравнение Абрахама М.: 1.1 КОНСТАНТЫ ХИМИЧЕСКИХ РАВНОВЕСИЙ ДИССОЦИАЦИИ И КОМПЛЕКСООБРАЗОВАНИЯ Термодинамические константы диссоциации (рKd = – lgKd) слабых органических кислот (НА = Н+ + А–) определяются на основании данных об электродвижущих силах (ЭДС) гальванических цепей без переноса Pt(H2)│HА (m1), NaА (m2), NaС1(m3), H2O-S│AgCl,Ag (I) по уравнению экстраполяцией Термодинамические константы образования комплексов краун-эфира (L) с катионами (М+ + L = LМ+) рассчитываются на основании данных об электродвижущих силах (ЭДС) гальванических цепей без переноса Мембранный эл-д (М+)│МСl (m1), L (m2), H2O-S│AgCl,Ag (II) по уравнению 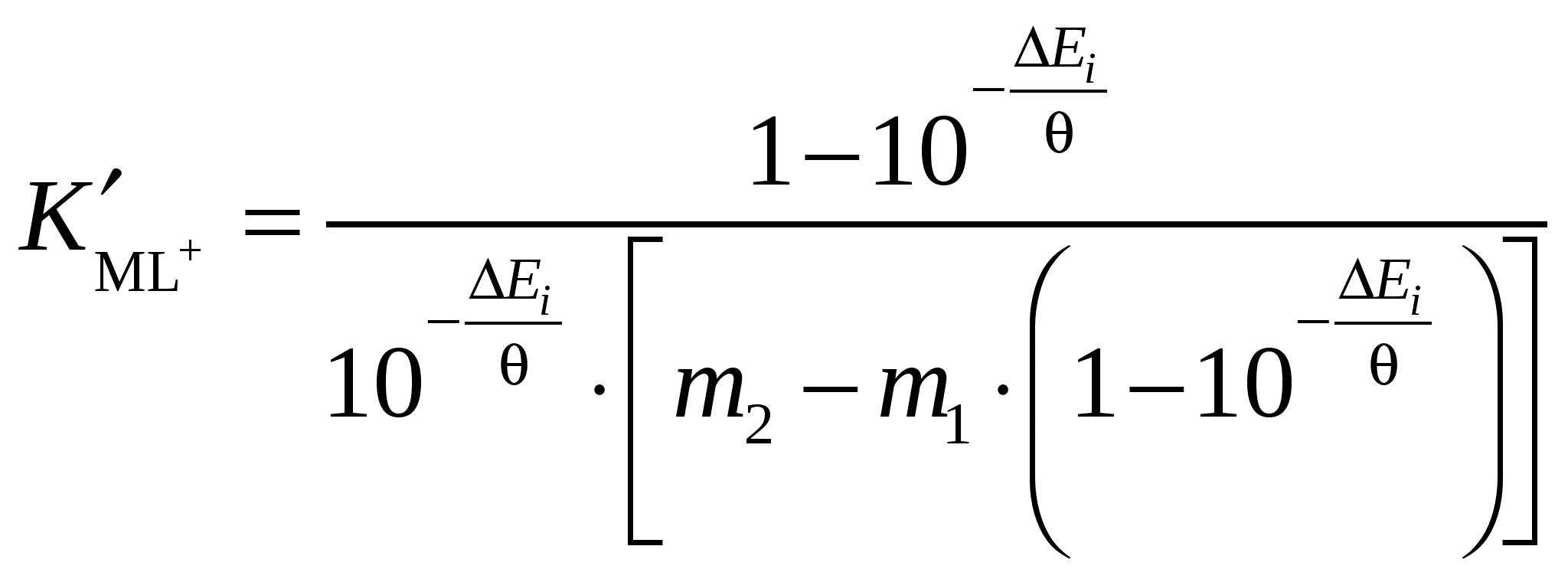 , (5) , (5)как среднеарифметическое значений 1.2 СТАТИСТИЧЕСКИЙ АНАЛИЗ ЗАВИСИМОСТИ Среднеарифметическое нескольких (n) независимых определений Доверительный интервал оценивается по уравнению где 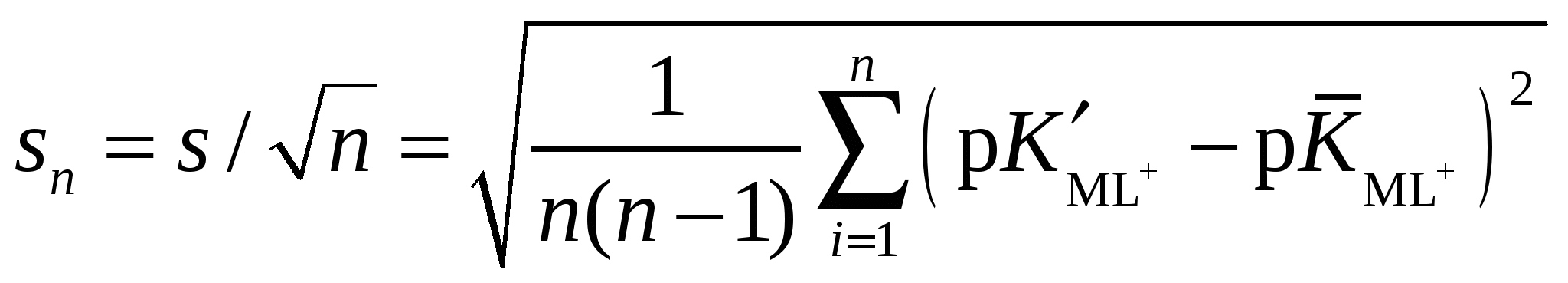 ; ; 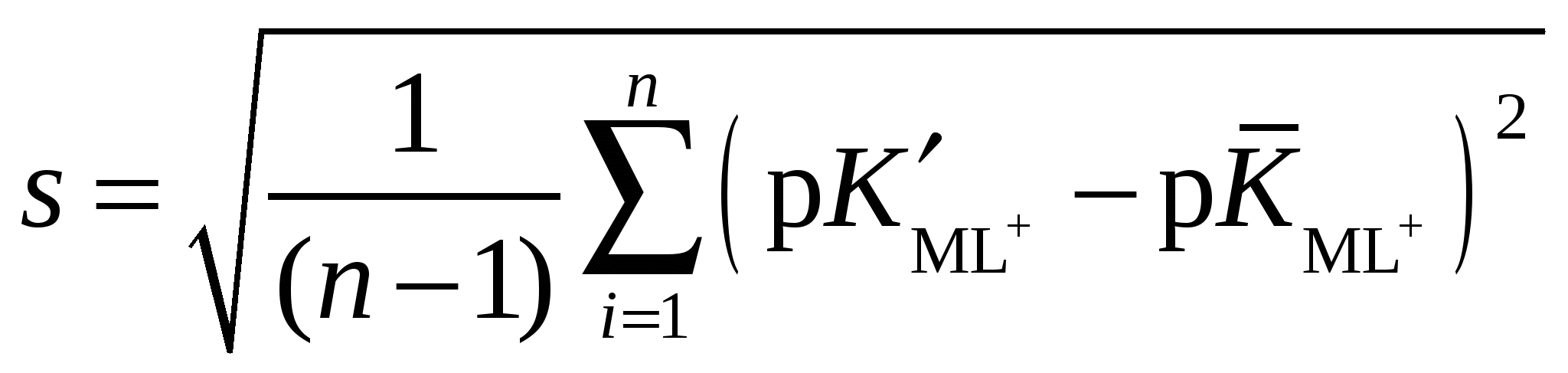 – среднеквадратичное (стандартное) отклонение. – среднеквадратичное (стандартное) отклонение.1.2.1 ВЫБОР ОПТИМАЛЬНОЙ ЗАВИСИМОСТИ КОНСТАНТЫ ХИМИЧЕСКОГО РАВНОВЕСИЯ ОТ ИОННОЙ СИЛЫ (ТЕМПЕРАТУРЫ) ПО КРИТЕРИЮ ФИШЕРА Статистический подход к выбору оптимальной зависимости между исследуемыми величинами (аппроксимирующей функции) основан на сопоставлении дисперсий аппроксимации с критерием Фишера. F - критерий Фишера вычисляется по формуле: где Если вычисленное значение критерия Fнабл = Температурная зависимость термодинамических констант диссоциации слабых электролитов обычно аппроксимируется уравнением Харнеда-Робинсона Температурная зависимость термодинамических констант устойчивости коронатов натрия, калия, аммония и серебра (I), как правило, аппроксимируется линейным уравнением 1.2.2 ПРОВЕРКА ЗНАЧИМОСТИ УРАВНЕНИЯ И КОЭФФИЦИЕНТОВ РЕГРЕССИИ Для проверки значимости уравнений регрессии (8) и (9) применяется критерий дисперсионного анализа (F – критерий). Проверка нулевой гипотезы H0: A = B = 0 проводится на основе статистики: 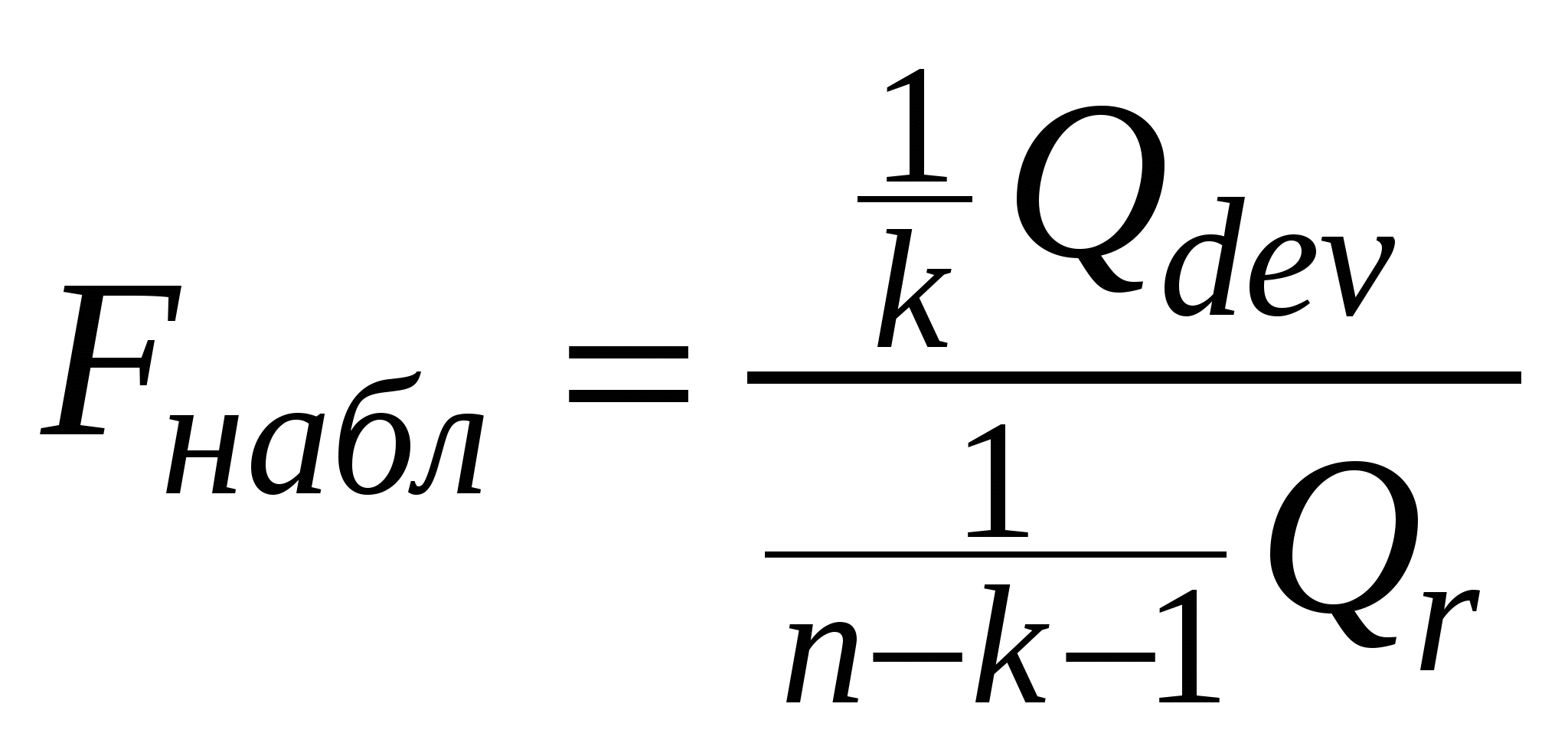 , (10) , (10)которая при выполнении гипотезы H0 имеет F-распределение с 1 = k и 2 = n-k-1 степенями свободы. Здесь n – число экспериментальных точек, k – число коэффициентов уравнения регрессии без свободного члена; Qdev – сумма квадратов отклонений 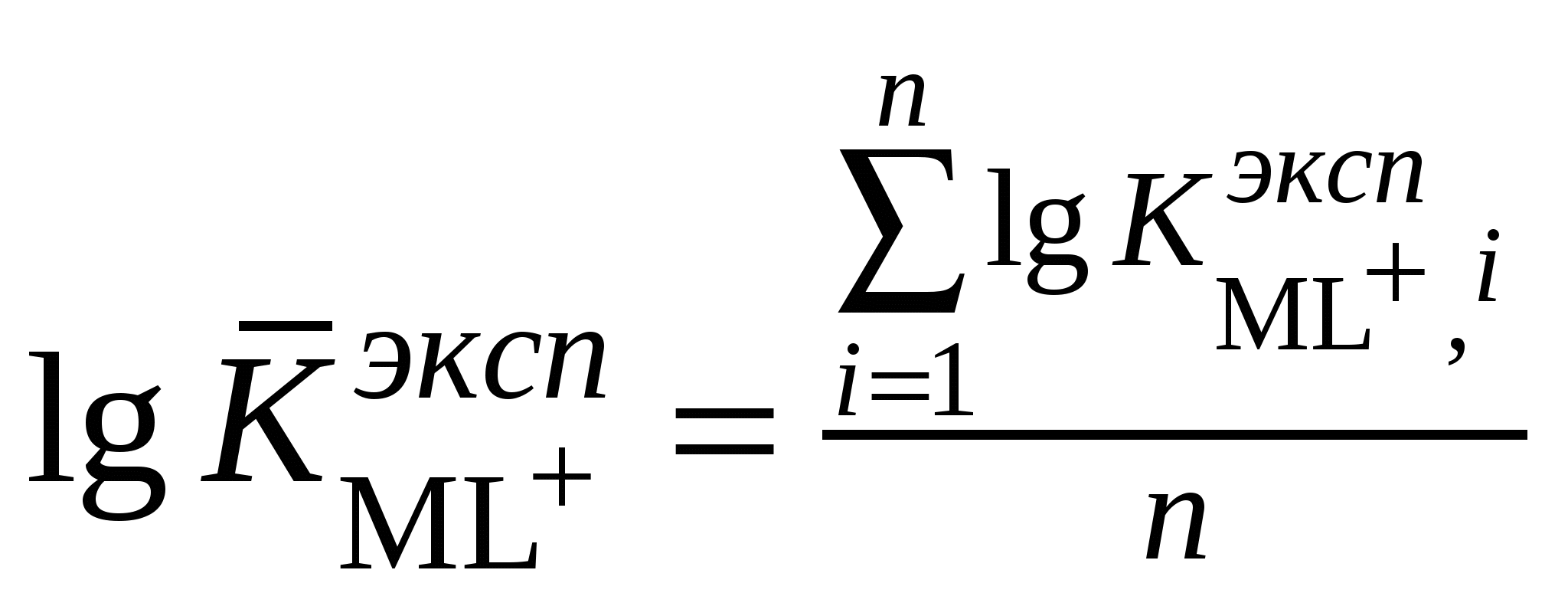 : : 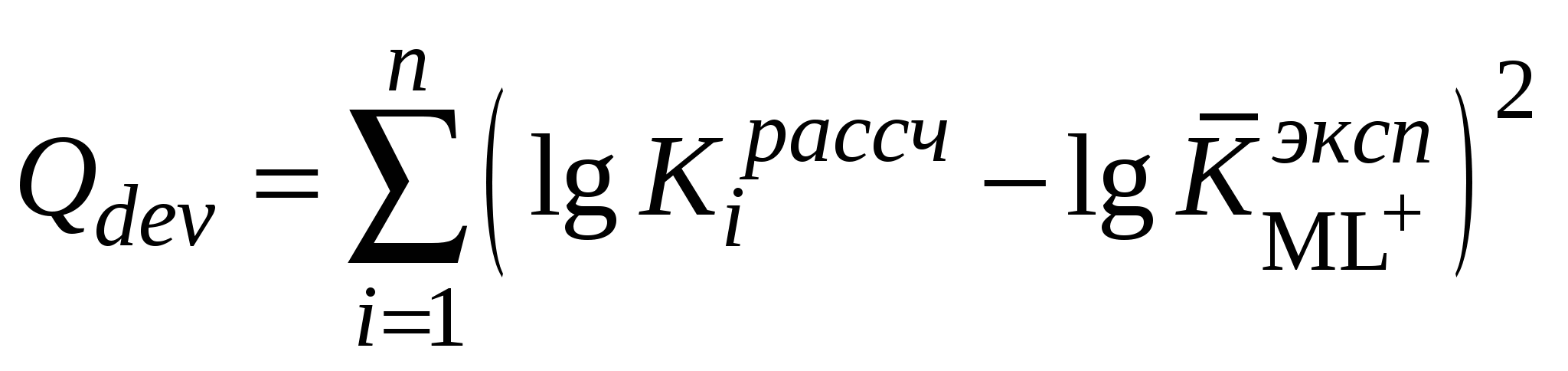 ; Qr – сумма квадратов отклонений экспериментальных ; Qr – сумма квадратов отклонений экспериментальных 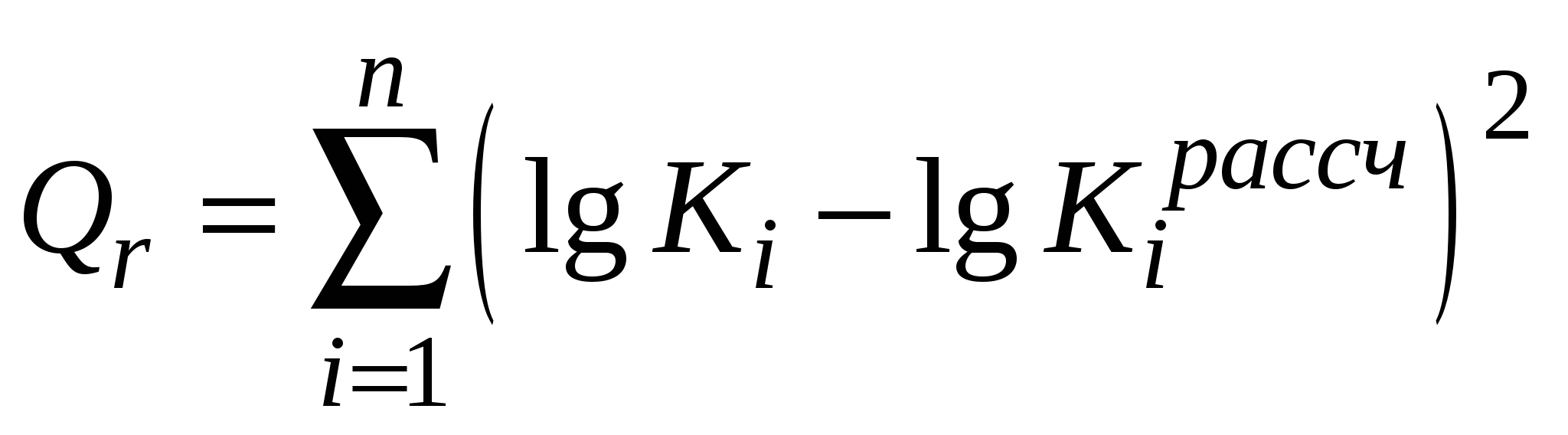 . Если Fнабл > Fкр, гипотеза H0: A = B = 0 отвергается, т.е. хотя бы один из коэффициентов уравнения регрессии не равен нулю. . Если Fнабл > Fкр, гипотеза H0: A = B = 0 отвергается, т.е. хотя бы один из коэффициентов уравнения регрессии не равен нулю.Проверка значимости коэффициентов регрессии (8) и (9) A и В проводится по t – критерию. Гипотеза H0: Ai= 0, Для линейного уравнения 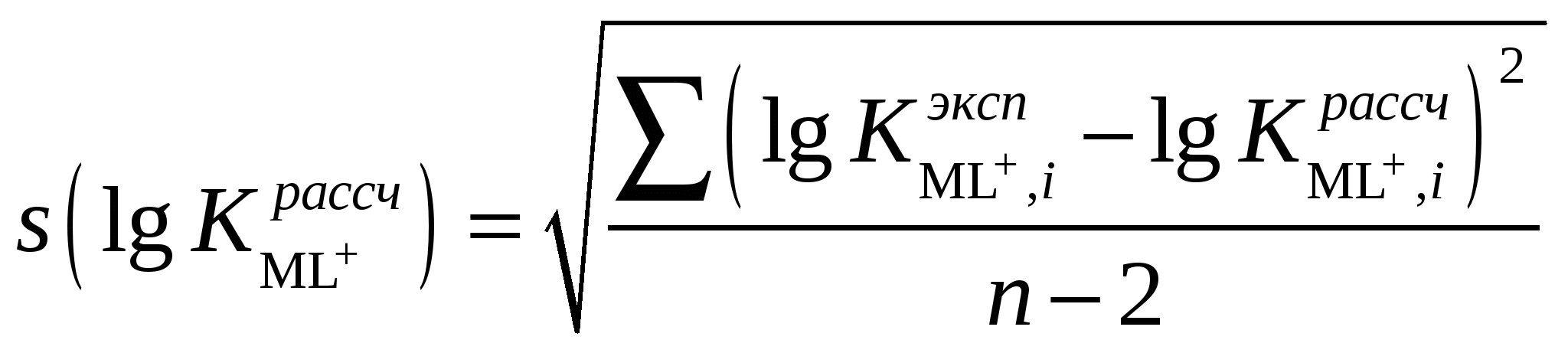 , ,Найдя 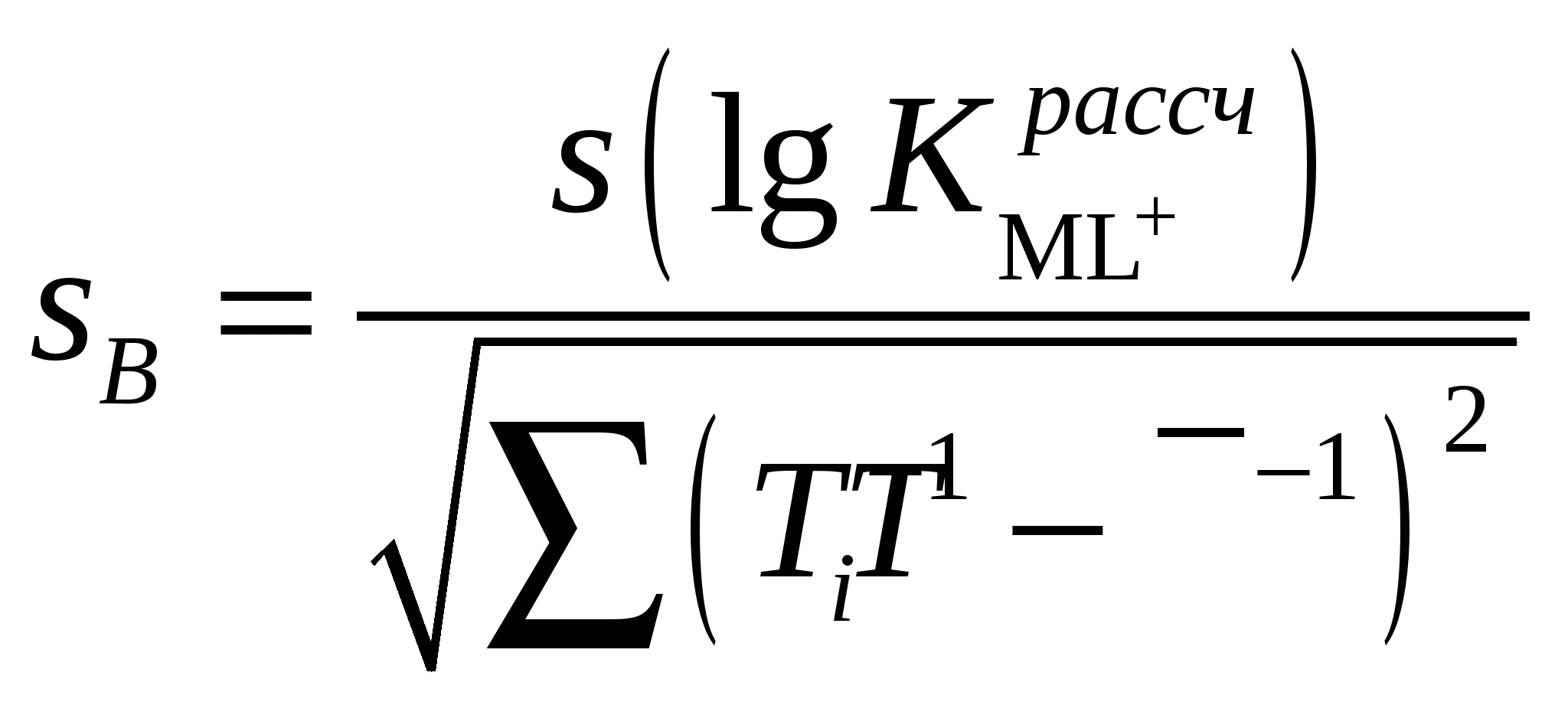 и стандартное отклонение коэффициента A 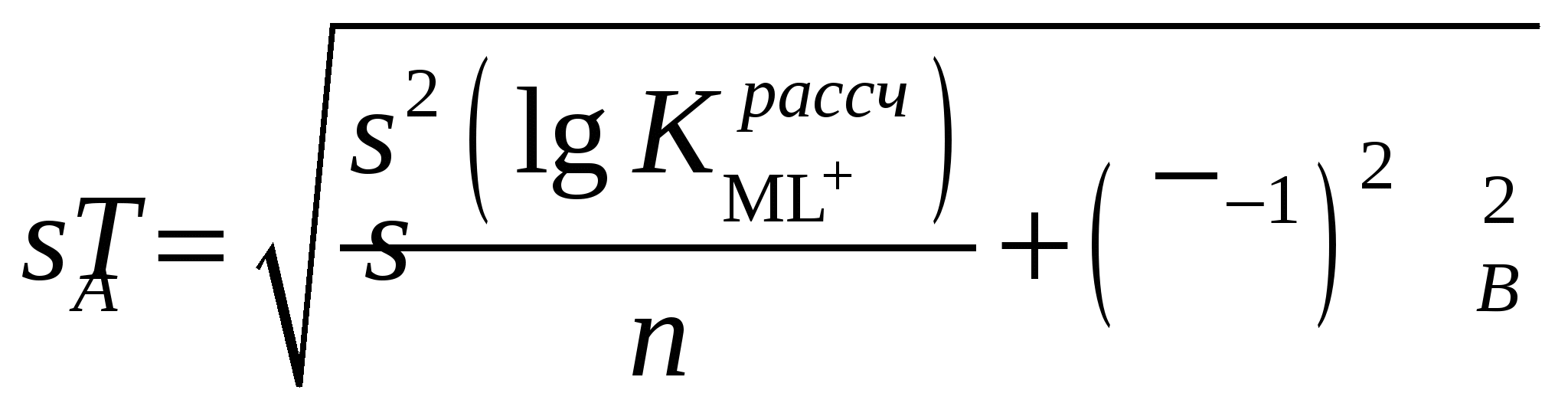 , ,где 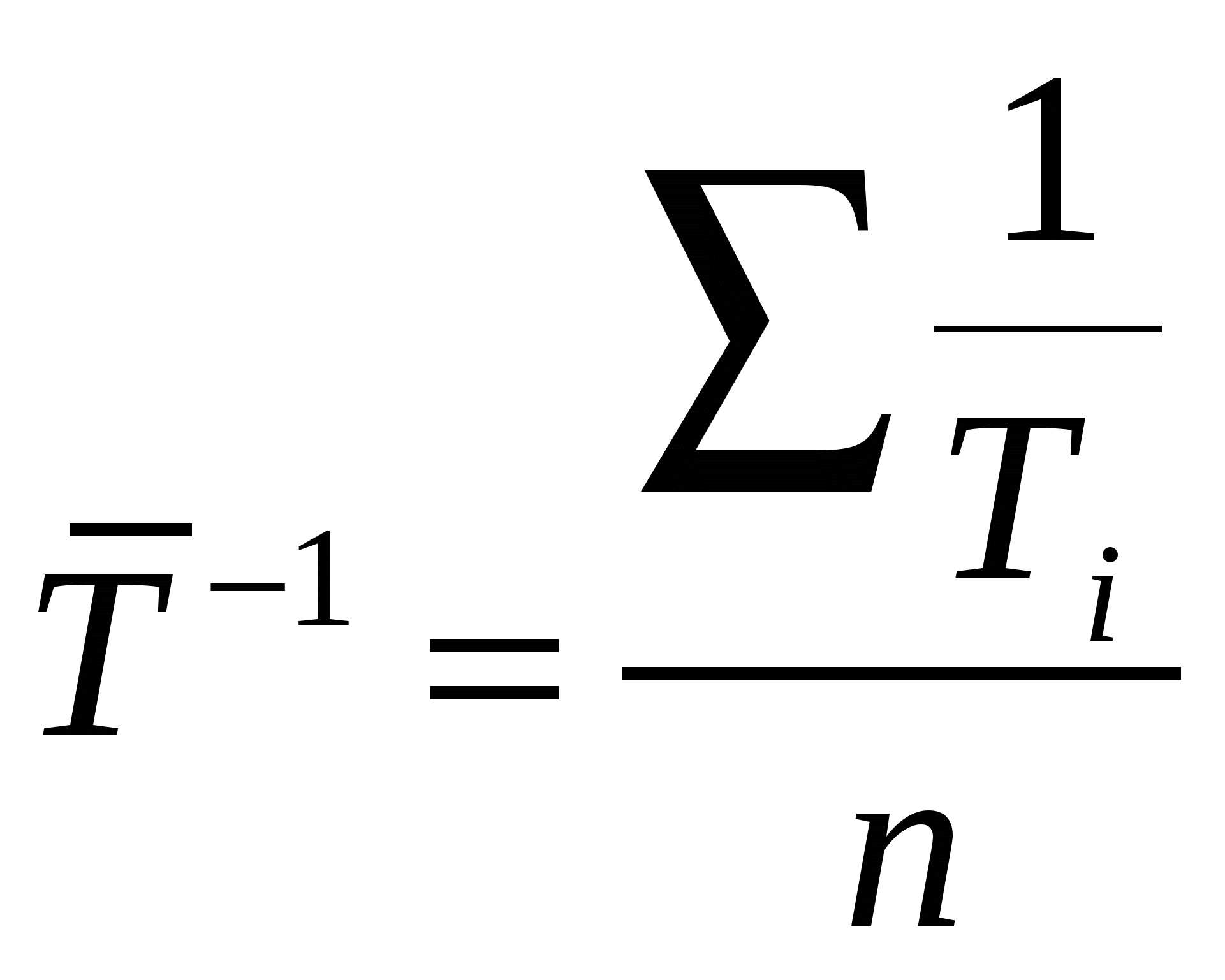 – среднее арифметическое значение обратной температуры. – среднее арифметическое значение обратной температуры. При статистическом анализе физико-химических данных нередко возникает необходимость в предварительной проверке соблюдения линейной зависимости между измеряемыми величинами. Степень близости корреляционной связи переменных к линейной зависимости, например  , ,или  где xi – значение параметра 1.3 ТЕРМОДИНАМИКА ХИМИЧЕСКИХ РАВНОВЕСИЙ Стандартные термодинамические характеристики диссоциации кислот (кДжмоль-1) рассчитываются по уравнениям: – энергии Гиббса – энтальпии диссоциации – энтропии диссоциации (Джмоль-1K-1) Стандартные термодинамические характеристики реакции комплексообразования рассчитываются по соотношениям: где M Na+, K+, NH4+ или Ag+. Доверительные интервалы для коэффициентов уравнения регрессии (8) оцениваются по формулам: A1 tn-k-1 Доверительные границы для термодинамических характеристик равновесий комплексообразования рассчитываются по соотношениям: rGо 2.303RTlgK, где lgK – доверительный интервал констант равновесия; rНо 2.303tn-k-1sBR; rSо 2.303tn-k-1sAR. 1.4 ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА ТЕРМОДИНАМИКУ ХИМИЧЕСКИХ РАВНОВЕСИЙ В наибольшей степени целям исследования влияния природы растворителя на термодинамические характеристики растворенного вещества соответствует нормировка стандартного состояния растворенного вещества (реагента химического равновесия) по его бесконечно разбавленному раствору. За стандартное состояние растворенного вещества в реальном растворе принимается его состояние в гипотетическом идеальном растворе (2 = 1) единичной концентрации, в котором парциальные мольный объем, энтальпия и теплоемкость такие же, как в бесконечно разбавленном растворе. Термодинамическое поведение реагента химического равновесия в растворе характеризуется значением химического потенциала 2 2 = 2о(с) + RT ln c = 2о(m) + RT ln m = 2о(X) + RT ln X = 2о(Csm) + RT ln Сsm (11) Соотношение (11) можно записать в виде 2о(Csm) = 2о(с) + RT ln c/Сsm = 2о(m) + RT ln m/Csm = 2о(X) + RT ln X/Csm(12) Из соотношения (11) с учетом (12) вытекает 2о(Csm) = 2о(с) + RT ln /(55.51M1 ) = = 2о(m) – RT ln 55.51M1 = 2о(X) + RT ln X1/55.51 Откуда 2о(с) = 2о(Csm) – RT ln /(55.51M1 ) 2о(m) = 20(Csm) + RT ln 55.51M1 2о(X) = 2о(Csm) – RT ln X1/55.51. Следовательно, химические потенциалы реагентов химического равновесия, стандартизованные к бесконечному разбавлению по шкале молярностей 2о(c) или моляльностей 2о(m) включают в себя две составляющие: – первая составляющая 2о(Сsm) не зависит от выбора концентрационной шкалы и отражает энергетические и структурные изменения, происходящие с реагентом и растворителем, при образовании раствора; – вторые слагаемые (RT ln /(55.51M1 ) и RT ln 55.51M1) не являются термодинамической характеристикой растворенного реагента, а следовательно и химического равновесия, так как они зависят от плотности и молярной массы растворителя. Для сопоставительного анализа термодинамических функций процессов и переноса вещества из одного растворителя в другой в качестве универсальной используется шкала сольвомоляльностей, поскольку при переходе от одного растворителя к другому сохраняется постоянным отношение количества молей растворенного вещества и растворителя. Сольвомоляльность является рациональным, безразмерным параметром состава раствора и вычисляется по формуле Сsm = 55.51(n2/n1), где n1 и n2 – число молей растворителя и растворенного вещества. Множитель 55.51 равен количеству вещества Н2О в одном кг воды. Если в качестве растворителя сравнения выбирается вода, шкала называется аквамоляльной. Соотношения для пересчета общеупотребительных концентраций на сольвомоляльность имеют вид Здесь М1 и М2 – молярные массы растворителя и растворенного вещества соответственно, кгмоль-1; р – плотность раствора, кгдм-3; m – моляльность, моль(1 кг растворителя)-1; с – молярная концентрация, моль дм-3; X – мольная доля. Kонстанты химических равновесий, выраженные в различных концентрационных шкалах, связаны соотношением  (12) (12)из которого следует, что константа равновесия не зависит от выбора единиц измерения концентраций только в случае, когда стехиометрический состав исходных веществ и продуктов реакции остается неизменным ( = 0). Константы равновесий диссоциации (HA = H+ + A–, = 1) и комплексообразования (М+ + L = LМ+, = –1), стандартизированные в сольвомоляльной, моляльной, молярной и мольно-долевой шкалах связаны соотношениями: – диссоциация lgKd(Csm) = lgKd(m) + lg(MWS/MW) lgKd(Csm) = lgKd(с) + lg(MWS/0MW ) lgKd(Csm) = lgKd(X) – lgMW – комплексообразование lgKLM(Csm) = lgKLM(m) – lg(MWS /MW) lgKLM(Csm) = lgKLM(с) – lg(MWS/0MW ) lgKLM(Csm) = lgKLM(X) + lgMW 1.5 ТЕРМОДИНАМИКА ПЕРЕСОЛЬВАТАЦИИ (ПЕРЕНОСА) РЕАГЕНТОВ В настоящее время для интерпретации влияния природы растворителя на термодинамические параметры равновесных химических реакций используются две концентрационные шкалы: – мольно-долевая (рациональная), X – содержание реагента выражается отношением числа молей растворенного вещества к определенному и одинаковому числу молей раствора; – сольвомоляльная, Сsm – содержание реагента выражается отношением числа молей растворенного вещества к определенному и одинаковому числу молей растворителя сравнения. Применение сольвомоляльной концентрационной шкалы позволяет проводить сопоставительный анализ термодинамических функций переноса реагентов химических равновесий из одного растворителя в другой при постоянстве числа молей растворителя (55.51 – если в качестве среды сравнения выбрана вода). Для стандартного химического потенциала реагента химического равновесия можно записать 2 = 2о(Сsm) + RT ln Сsm = 2о(m) + RT ln m Так как в водных растворах Сsm = m, то 2о,W(Сsm) = 2о,W(m). Следовательно, сольвомоляльная концентрационная шкала удобна тем, что для воды она идентична достаточно распространенной в термодинамике растворов шкале моляльностей. Поэтому во многих случаях отпадает необходимость пересчета имеющихся для водных растворов термодинамических данных к сольвомоляльной концентрации. В водно-органических растворителях 2о,SW(Сsm) = 2о,SW(m) + RT ln m / Сsm= 2о,SW(m) – RT ln 55.51MSW MSW = X1Mw + X2MS В водной среде 2о,W(Сsm) = 2о,W(m) + RT ln m / Сsm= 2о,W(m) – RT ln 55.51Mw = 2о,W(m) 1.6 ВЗАИМОСВЯЗЬ МЕЖДУ СТАНДАРТНЫМИ ТЕРМОДИНАМИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ РАВНОВЕСИЙ ДИССОЦИАЦИИ СЛАБЫХ ОРГАНИЧЕСКИХ КИСЛОТ В РАЗНЫХ КОНЦЕНТРАЦИОННЫХ ШКАЛАХ HA = H+ + A– |
