зачет 8 класс геометрия. Тесты для контроля качества усвоения теоретического материала по геометрии для учащихся 8 класса. Тематика и содержание тестов соответствуют требованиям программы по геометрии для учащихся 8 класса
 Скачать 262.71 Kb. Скачать 262.71 Kb.
|
|
ТЕМА: ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА, РОМБА И ТРЕУГОЛЬНИКА ВАРИАНТ 1 А1. Стороны параллелограмма равны 10 см и 6 см, а угол между этими сторонами равен 150°. Чему равна площадь этого параллелограмма? 1) 60 см2 2) 30 см2 3) 15 см2 4) 120 см2 Ответ: 2. А2. Чему равна площадь ромба, диагонали которого равны 8 см и 6 см? 1) 12 см2 2) 48 см2 3) 96 см2 4) 24 см2 Ответ: 4. А3. Две стороны треугольника равны 10 см и 14 см, а угол между ними 30°. Чему равна площадь треугольника? 1) 27 см2 2) 108 см2 3) 54 см2 4) 35 см2 Ответ: 4. А4. Стороны параллелограмма 10 см и 8 см, меньшая высота 4 см. Найдите большую высоту параллелограмма. 1) 3 см 2) 5 см 3) 6 см 4) 4 см Ответ: 2. В1. В треугольнике АВС угол А = 45°, ВС = 10 см, а высота BD делит сторону АС на отрезки AD = 6 см, DC = 8 см. Найдите площадь треугольника и высоту, проведенную к стороне ВС. Ответ: 42 см2; 8,4 см. В2. В треугольнике АВС угол А = 75°, угол В = 30°, АВ = 12 см. Найдите площадь треугольника. Ответ: 36 см2. С1. Высоты, проведенные из вершины тупого угла параллелограмма, составляют угол, равный 45°. Одна из высот делит сторону, на которую она опущена, на отрезки 3 см и 7 см, считая от вершины острого угла. Найдите площадь параллелограмма. Ответ: 30 см2. Вариант2 А1. Стороны параллелограмма равны 12 см и 8 см, а угол между этими сторонами равен 30°. Чему равна площадь этого параллелограмма? 1) 192 см2 2) 96 см2 3) 24 см2 4) 48 см2 Ответ: 4. А2. Чему равна площадь ромба, диагонали которого равны 10 см и 12 см? 1) 60 см2 2) 120 см2 3) 30 см2 4) 240 см2 Ответ: 1. А3. Найдите площадь треугольника, две стороны которого равны 6 см и 8 см, а угол между ними 30°. 1) 48 см2 2) 12 см2 3) 96 см2 4) 24 см2 Ответ: 2. А4. Высоты параллелограмма 6 см и 8 см, большая сторона 12 см. Найдите меньшую сторону параллелограмма. 1) 10 см 2) 9 см 3) 16 см 4) 4 см Ответ: 2. В1. В треугольнике АВС угол С = 45°, АВ = 10 см, а высота AD делит сторону СВ на отрезки CD = 8 см, DВ = 6 см. Найдите площадь треугольника и высоту, проведенную к стороне АВ. Ответ: 56 см2; 11,2 см. В2. В треугольнике АВС угол А = углу В = 75°. Найдите длину ВС, если площадь треугольника равна 25 см2. Ответ: 10 см. С1. Высоты, проведенные из вершины тупого угла параллелограмма, составляют угол, равный 45°. Одна из высот делит сторону, на которую она опущена, на отрезки 5 см и 8 см, считая от вершины острого угла. Найдите площадь параллелограмма. Ответ: 65 см2. ТЕМА: ПЛОЩАДЬ ТРАПЕЦИИ ВАРИАНТ 1 А1. Основания трапеции равны 5 см и 9 см, ее высота - 5 см. Чему равна площадь трапеции? 1) 45 см2 2) 35 см2 3) 42 см2 4) 84 см2 Ответ: 2. А2. В равнобедренной трапеции основания равны 6 см и 12 см, а угол при основании равен 45°. Чему равна площадь трапеции? 1) 16 см2 2) 32 см2 3) 27 см2 4) 24 см2 Ответ: 3. А3. В прямоугольной трапеции основания равны 5 см и 9 см, а меньшая боковая сторона - 4 см. Чему равна площадь трапеции? 1) 36 см2 2) 56 см2 3) 14 см2 4) 28 см2 Ответ: 4. А4. Диагонали трапеции взаимно перпендикулярны и равны 10 см и 15 см. Чему равна площадь трапеции? 1) 75 см2 2) 216 см2 3) 54 см2 4) 162 см2 Ответ: 1. В1. В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на два отрезка, больший из которых равен 26 см. Найдите площадь трапеции, если ее высота равна 10 см. Ответ: 260 см2. В2. В равнобедренной трапеции диагонали взаимно перпендикулярны, высота трапеции равна 12 см. Найдите площадь трапеции. Ответ: 144 см2. С1. Основания и высота трапеции относятся как 5 : 6 : 2. Найдите меньшее основание трапеции, если площадь трапеции равна 44 см2. Ответ: 10 см. С2. В трапеции ABCD BC и AD - основания, BC : AD = 3 : 4. Площадь трапеции равна 70 см2. Найдите площадь треугольника АВС. Ответ: 30 см2. Вариант2 А1. Основания трапеции равны 4 см и 8 см, ее высота - 9 см. Чему равна площадь трапеции? 1) 54 см2 2) 27 см2 3) 108 см2 4) 72 см2 Ответ: 1. А2. В равнобедренной трапеции основания равны 8 см и 16 см, а угол при основании равен 45°. Чему равна площадь трапеции? 1) 24 см2 2) 96 см2 3) 72 см2 4) 48 см2 Ответ: 4. А3. В прямоугольной трапеции основания равны 6 см и 10 см, а меньшая боковая сторона - 5 см. Чему равна площадь трапеции? 1) 80 см2 2) 40 см2 3) 20 см2 4) 30 см2 Ответ: 2. А4. Диагонали трапеции взаимно перпендикулярны и равны 14 см и 12 см. Чему равна площадь трапеции? 1) 168 см2 2) 224 см2 3) 56 см2 4) 84 см2 Ответ: 4. В1. В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на два отрезка, больший из которых равен 18 см. Найдите площадь трапеции, если ее высота равна 12 см. Ответ: 216 см2. В2. В равнобедренной трапеции диагонали взаимно перпендикулярны, высота трапеции равна 11 см. Найдите площадь трапеции. Ответ: 121 см2. С1. Высота трапеции равна меньшему основанию и в два раза меньше большего основания. Найдите высоту трапеции, если ее площадь равна 54 см2. Ответ: 6 см. С2. В трапеции ABCD BC и AD - основания, ВС : AD = 4 : 5. Площадь треугольника ACD равна 35 см2. Найдите площадь трапеции. Ответ: 63 см2. ТЕОРЕТИЧЕСКИЙ ТЕСТ ПО ГЕОМЕТРИИ ТЕМА: ПЛОЩАДЬ А1. Выберите верное утверждение: 1) если два многоугольника имеют равные площади, то они равны 2) если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников 3) квадратный сантиметр - это фигура, стороны которой равны 1 см 4) площадь квадрата равна произведению его сторон Ответ: 2. А2. Высотой трапеции называется: 1) перпендикуляр, проведенный к его основанию 2) отрезок, пересекающий основание трапеции под прямым углом 3) перпендикуляр, опущенный из вершины трапеции 4) перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание Ответ: 4. А3. Если высоты двух треугольников равны, то: 1) их площади относятся как основания 2) их площади равны 3) эти треугольники равны 4) основания, к которым они проведены, равны Ответ: 1. А4. Площадь параллелограмма равна: 1) произведению стороны параллелограмма на высоту 2) произведению его основания на высоту, проведенную к данному основанию 3) половине произведения его основания на высоту, проведенную к данному основанию 4) произведению смежных сторон параллелограмма Ответ: 2. А5. Площадь прямоугольного треугольника равна: 1) произведению его катетов 2) произведению его гипотенузы на один из его катетов 3) половине произведения его катетов 4) произведению стороны на высоту Ответ: 3. А6. Площадь трапеции равна: 1) произведению полусуммы оснований на половину высоты 2) произведению суммы оснований на высоту 3) произведению суммы оснований на половину высоты 4) произведению оснований и высоты Ответ: 3. А7. Теорема Пифагора гласит: 1) в прямоугольном треугольнике гипотенуза равна сумме катетов 2) в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов 3) в прямоугольном треугольнике квадрат гипотенузы равен сумме катетов 4) если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный Ответ: 2. А8. Если в треугольнике АВС АС2 = АВ2 + ВС2, то: 1) угол В прямой 2) угол С прямой 3) угол А прямой 4) угол С или угол А прямой Ответ: 1. А9. Египетским называется треугольник, длины сторон которого: 1) удовлетворяют теореме Пифагора 2) удовлетворяют теореме, обратной теореме Пифагора 3) равны 3, 4 и 5 4) равны целым числам Ответ: 3. А10. Как записывается формула Герона для вычисления площади треугольника АВС со сторонами a, b и с? 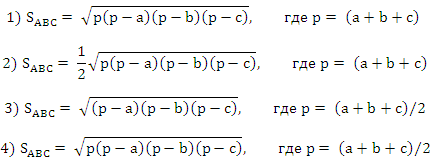 Ответ: 4. ОБОБЩЕНИЕ ТЕМЫ "ПЛОЩАДЬ" ВАРИАНТ 1 А1. Сторона ромба равна 5 см, а одна из его диагоналей - 6 см. Чему равна площадь ромба? 1) 30 см2 2) 24 см2 3) 15 см2 4) 12 см2 Ответ: 2. А2. Биссектриса угла А прямоугольника ABCD пересекает сторону ВС в точке Е так, что ВЕ = 4,5 см, СЕ = 5,5 см. Чему равна площадь прямоугольника? 1) 55 см2 2) 100 см2 3) 110 см2 4) 45 см2 Ответ: 4. А3. Чему равна площадь ромба со стороной 8 см и углом, равным 60°? 1) 32 см2 2) 32√3 см2 3) 38 см2 4) 16√3 см2 Ответ: 2. А4. Чему равна площадь прямоугольного треугольника с гипотенузой 26 см, один из катетов которого равен 24 см? 1) 120 см2 2) 60 см2 3) 312 см2 4) 240 см2 Ответ: 1. А5. Одна из сторон треугольника равна 16 см, а высота, проведенная к ней, - 9 см. Чему равна высота, проведенная к стороне треугольника, равной 24 см? 1) 5 см 2) 12 см 3) 13 см 4) 6 см Ответ: 4. А6. Площадь квадрата равна 48 см2. Чему равен периметр данного квадрата? 1) 12√3 см 2) 8√3 см 3) 16√3 см 4) 144 см Ответ: 3. А7. Площадь ромба равна 36 см2, а одна из его диагоналей в два раза меньше другой. Чему равна сторона ромба? 1) 3 см 2) 3√5 см 3) 3√3 см 4) 3√2 см Ответ: 2. В1. В трапеции ABCD угол А = 60°, угол D = 45°, основание ВС равно 3 см, BF и СЕ - высоты трапеции, ED = 4 см. Найдите площадь трапеции. Ответ: SABCD = 4(5 + 2√3/3)см2. В2. В треугольнике АВС биссектриса AD равна 7 см, АВ = 6 см, АС = 8 см. Найдите SABD : SACD. Ответ: SABD : SACD = 3 : 4. В3. В трапеции ABCD основания ВС и AD равны 8 см и 12 см, диагональ АС равна 40 см и пересекает диагональ BD в точке О. Найдите разность АО и СО. Ответ: 8 см. С1. В параллелограмме ABCD диагональ BD перпендикулярна стороне АВ, один из углов параллелограмма равен 120°, AD = 12 см, О - точка пересечения диагоналей. Найдите диагонали параллелограмма и площадь треугольника CDO. Ответ: АС = 6√7; BD = 6√3 см; SCDO = 9√3 см2. С2. В прямоугольной трапеции ABCD меньшее основание равно меньшей боковой стороне. Диагональ, проведенная из вершины тупого угла, перпендикулярна большей боковой стороне, равной 8√2 см. Найдите периметр и площадь трапеции. Ответ: PABCD = 8(4 + √2) см; S = 96 см2. Вариант2 А1. Чему равна площадь квадрата со стороной 5√2 см? 1) 50 см2 2) 25 см2 3) 75 см2 4) 100 см2 Ответ: 1. А2. Биссектриса угла В прямоугольника ABCD пересекает сторону AD в точке К так, что АК = 6,5 см, KD = 3,5 см. Чему равна площадь прямоугольника? 1) 35 см2 2) 100 см2 3) 65 см2 4) 32,5 см2 Ответ: 3. А3. Чему равна площадь ромба со стороной 10 см и углом, равным 60°? 1) 50 см2 2) 50√3 см2 3) 100 см2 4) 25√3 см2 Ответ: 2. А4. Чему равна площадь равнобедренной трапеции с основаниями 10 см и 16 см и боковой стороной 5 см? 1) 104 см2 2) 52 см2 3) 42 см2 4) 65 см2 Ответ: 2. А5. Одна из сторон параллелограмма равна 14 см, а высота, проведенная к ней, - 12 см. Чему равна высота, проведенная к смежной стороне, равной 21 см? 1) 8 см 2) 12 см 3) 10 см 4) 19 см Ответ: 1. А6. Периметр квадрата равен 20√2 см. Чему равна площадь данного квадрата? 1) 200 см2 2) 25 см2 3) 100 см2 4) 50 см2 Ответ: 4. А7. Площадь прямоугольника равна 24 см2, а его стороны относятся как 2 : 3. Чему равна диагональ прямоугольника? 1) √13 см 2) 3√13 см 3) 2√13 см 4) 13 см Ответ: 3. В1. В трапеции ABCD угол А = 60°, угол D = 45°, основание ВС равно 5 см, BF и СЕ - высоты трапеции, ED = 4 см. Найдите площадь трапеции. Ответ: SABCD = 4(7 + 2√3/3) см2. В2. В треугольнике АВС биссектриса АН равна 8 см, АВ = 6 см, АС = 9 см. Найдите SABH : SACH. Ответ: 2 : 3. В3. В параллелограмме MNKP диагональ МК равна 20 см. Точки В и С - середины сторон NK и КР соответственно. Отрезок ВС пересекает диагональ МК в точке Е. Найдите разность МЕ и ЕК. Ответ: 10 см. С1. В треугольнике АВС через точку пересечения медиан проведена прямая, параллельная стороне АС и пересекающая стороны АВ и ВС в точках К и Е соответственно. Найдите АС, если КЕ = 12 см. Найдите площадь треугольника ВКЕ, если площадь треугольника АВС = 72 см2. Ответ: АС = 18 см; SBKE = 32 см2. С2. В равнобедренной трапеции MNKP диагональ МК является биссектрисой угла при нижнем основании МР. Меньшее основание NK равно 8 см. Найдите площадь трапеции, если один из углов в два раза меньше другого. В каком отношении высота КЕ делит основание МР? Ответ: SMNKP = 48√3 см2; МЕ : ЕР = 3 : 1. ИТОГОВЫЙ ТЕСТ ПО ГЕОМЕТРИИ ЗА 8 КЛАСС ВАРИАНТ 1 А1. Чему равна площадь равностороннего треугольника со стороной 8см? 1) 9 см2 2) 9√3 см2 3) 18 см2 4) 16√3 см2 Ответ: 4. А2. Биссектриса угла А параллелограмма ABCD делит сторону ВС на отрезки ВК = 5 см и КС = 3 см. Чему равен периметр параллелограмма? 1) 28 см 2) 15 см 3) 24 см 4) 30 см Ответ: 1. А3. В равнобедренной трапеции ABCD высота, опущенная из вершины В на большее основание AD, равна 4 см и делит AD на отрезки, равные 5 см и 9 см. Чему равна площадь трапеции? 1) 36 см2 2) 72 см2 3) 18 см2 4) 38 см2 Ответ: 1. А4. ABCD - квадрат со стороной 4 см. На сторонах АВ и CD отложены отрезки АМ и СК так, что АМ = СК = 3 см. Найдите периметр четырехугольника MBKD. 1) 14 см 2) 12 см 3) 10 см 4) 16 см Ответ: 2. В1. В трапеции ABCD основание ВС перпендикулярно боковой стороне АВ, угол D равен 60°, диагональ АС перпендикулярна стороне CD, равной 10 см. Найдите длину основания ВС. 1) 8 см 2) 15 см 3) 16 см 4) 4 см Ответ: 2. В2. В трапеции ABCD основания ВС и AD равны соответственно 6 см и 10 см. Диагональ АС, равная 32 см, пересекает диагональ BD в точке К. Найдите длину КС. Ответ: 12 см. С1. В параллелограмме ABCD АВ = 8 см, ВС = 12 см. Точки К и Е лежат соответственно на сторонах ВС и CD так, что СК = 3 см, СЕ = 2 см. Отрезок КЕ пересекает диагональ АС в точке Р. Найдите отношение АР к РС. Ответ: 7 : 1. Вариант2 А1. Чему равна площадь равностороннего треугольника, высота которого 9 см? 1) 13,5 см2 2) 13,5√3 см2 3) 6,75 см2 4) 27√3 см2 Ответ: 4. А2. Биссектриса угла В параллелограмма ABCD делит сторону AD на отрезки АЕ = 7 см и ED = 4 см. Чему равен периметр параллелограмма? 1) 28 см 2) 22 см 3) 36 см 4) 30 см Ответ: 3. А3. В равнобедренной трапеции ABCD высота, опущенная из вершины В на большее основание AD, равна 6 см и делит AD на отрезки, равные 3 см и 7 см. Чему равна площадь трапеции? 1) 84 см2 2) 42 см2 3) 21 см2 4) 26 см2 Ответ: 2. А4. ABCD - квадрат со стороной 8 см. На сторонах АВ и CD отложены отрезки АМ и КС так, что АМ = КС = 6 см. Найдите периметр четырехугольника MBKD. 1) 24 см 2) 32 см 3) 28 см 4) 36 см Ответ: 1. В1. В трапеции ABCD основание AD перпендикулярно боковой стороне АВ, диагональ АС перпендикулярна стороне CD. Найдите длину стороны CD, если ВС = 6 см, угол ВСА = 30°. 1) 6 см 2) 4√3 см 3) 12 см 4) 4 см Ответ: 4. В2. В трапеции ABCD основания ВС и AD равны соответственно 8 см и 12 см. Диагональ BD, равная 25 см, пересекает диагональ АС в точке Е. Найдите длину ВЕ. Ответ: 10 см. С1. В параллелограмме ABCD АВ = 6 см, ВС = 9 см. Точки К и Е лежат соответственно на сторонах ВС и CD так, что СК = 6 см, СЕ = 4 см. Отрезок КЕ пересекает диагональ АС в точке Р. Найдите отношение АР к РС. Ответ: 2 : 1. Литература 1.А.Н.Шыныбеков.Учебник геометрии для 8 класса. Алматы «Атамура» 2004год 2.Е.М.Рабинович.Задачи и упражнения на готовых чертежах.7-9классы «Илекса», «Гимназия» Москва- Харьков 2002год 3.К.Н.Бексултанова,К.И.Черенко.Готовые задания, решения, ответы по математике. «Келешек-2030»2009 год |
