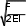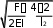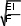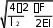цуыв. Тестовые задания по разделам изучения содержания дисциплины
 Скачать 250.83 Kb. Скачать 250.83 Kb.
|
В: ФАЙЛ + В: ФАЙЛ - В: ФАЙЛ - В: ФАЙЛ -z4 4 pz2 4r 0 z4 4 pz2 4r 0 z4 4 pz2 r 0 z4 pz2 4r 0 ВЫБОРСпособы измерения продольных сил в упругих стержнях … В+ Механический, основанный на законе Гука В- С помощью ультразвука В- С помощью магнитострикции В- С помощью аудиоэмиссии ВЫБОРСпособы изменения продольных сил в упругих стержнях … В+ Полное раскрепление при необходимой температуре В- Локальное раскрепление В- Перезакрепление от середины к концу В- С помощью натяжения ВЫБОРСпособы изменения длины упругих стержней … В+ С помощью сварки В- Локальное раскрепление В- Перезакрепление от середины к концу В- С помощью натяжения Раздел 04_Математические модели, состояния упругих стержней в вязкой среде. ВЫБОРДифференциальное уравнение изменений поперечных перемещений под дей- ствием продольных сжимающих сил в бесстыковом пути для модели, учитывающей воздействие поездов будет иметь следующий вид … В: ФАЙЛ + В: ФАЙЛ -EI 0
EI 0 В: ФАЙЛ - В: ФАЙЛ -4 y  EIx4 EIx44 y  EIx4 EIx42 y  Fx2 2 y  Fx2 Fx2 y 0   y 0 y 0 ВЫБОРДифференциальное уравнение изменений поперечных перемещений в бесстыковом пути под действием продольных растягивающих сил для модели, учитывающей воздействие поездов будет иметь следующий вид …
В: ФАЙЛ + EI 0 В: ФАЙЛ - В: ФАЙЛ - В: ФАЙЛ -EI 0 EI 0 EI 0 ВЫБОРРешение однородного дифференциального уравнения в частных производных с постоянными коэффициентами, отражающее устойчивость упругого стержня в вязкой среде, может быть найдено методом Фурье, как произведение двух функций … В: ФАЙЛ + В: ФАЙЛ - В: ФАЙЛ - В: ФАЙЛ -y x, U x f y x, U x f x y x, U f y U x f ВЫБОРФункция f(τ), определяющая изменение во времени продольных сил в упругом стержне … В: ФАЙЛ + f Qf 0 В: ФАЙЛ - f Q 0 В: ФАЙЛ - f f 0 В: ФАЙЛ -f Qf 0 ВЫБОРРешение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил в упругом стержне в вязкой среде имеет вид …  2x 2x 4EI F 42 2 В: ФАЙЛ +y x, Аch xcos exp 2     l 4EI l 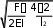 4EI F 42 2 4EI F 42 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 y | F | 2 y | | y 0 |
| x4 4 y | F | x2 2 y | | y F |
| x4 4 y | F | x2 2 y | | R y F |
EIEI
2 yFx2
y F

 R
RВ: ФАЙЛ -
EIx4
x2

R
ВЫБОР
Решение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил в упругом кривом стержне в вязкой среде имеет вид …
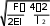 x
x 4EI F
42 2
l2
4x2
В: ФАЙЛ +
y x, Ach
xcos exp
1 2
l
4EI l 8R l
2
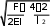 4EI F
4EI F 42 2
l2
4x2
В: ФАЙЛ -
y x, Ach
xexp
1 2
4EI l
8R l
2
2
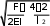 x
x 4EI F
42 2 l2
В: ФАЙЛ -
y x, Ach
xcos exp
l
4EI l 8R

В: ФАЙЛ -
xl2
4x2
y x, Ach
xcos l
8R1 l2
ВЫБОР
Решение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил в упругом кривом стержне в вязкой среде имеет вид для точки х = 0 …
4EI F 42 2 l2
2
В: ФАЙЛ +
y0,
f0 exp




4EI l 8R
4EI F2 l2



В: ФАЙЛ -
y0,
f0 exp
4EI
8R
4EI F 42 l2
В: ФАЙЛ -
y0,
f0 exp
4EI l2
8R




4EI F 42 2 l2
2
В: ФАЙЛ -
y0, exp




4EI l 8R
ВЫБОР
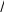 Решение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил упругом кривом стержне в вязкой среде имеет вид для точки х = 0 при l2 42EIF…
Решение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил упругом кривом стержне в вязкой среде имеет вид для точки х = 0 при l2 42EIF… 6, 25F2 2EI
В: ФАЙЛ +
y0,
f0 exp
EI
2RF


6, 25F2 2EI
В: ФАЙЛ -
y0,
f0 exp
EI
2RF


6, 25F2 EI
В: ФАЙЛ -
y0,
f0 exp
EI
2RF


6, 25F2
2EI
В: ФАЙЛ -
y0, exp
EI
2RF


ВЫБОР
Опасная скорость роста стрелы изгиба упругого стержня в плане определяется по формуле …
6, 25 fF2 6, 25F2
В: ФАЙЛ +
y0, 0 exp
EI

EI
В: ФАЙЛ -
y0,
6, 25F2
 EI
EIexp
6, 25F2

EI
6, 25 fF2 6, 25F2
В: ФАЙЛ -
y0, 0 exp
EI

EI
6, 25 fF2 6, 25F2
В: ФАЙЛ -
y0, 0 exp
 EI EI
EI EIВЫБОР
Изменение погонных сопротивлений среды, в которой находится упругий стержень при постоянной скорости роста деформаций (w) …
0
x
В: ФАЙЛ + r reτ/ n nU
H 1 eτ/n w
0
В: ФАЙЛ - В: ФАЙЛ -
r re / n nUr re / n U
H1 e / n
0
x
x
x
H1 e / nw
0
В: ФАЙЛ -
r re / n nU
H1 e / nw
ВЫБОР
Для случая периодического изменения rили λпо гармоническому закону,
характерного для концевого участка упругого стержня
r rosin …
2
В: ФАЙЛ + 2
r2
r2
2cos r
r
sin 2
o o o o
2
В: ФАЙЛ - 2
r2
r2
2 cos r
r
sin