VI. Модель 3-х фазного тетра-инвертора и вычислителем условного прогноза по каждой фазе в терминологии программ "ELTRAN".
Название модели: [3F-Tetra_Inv.trn].
'3-х ф. тетра-инвертор с ШИМ-2, с условным прогнозом,
при NТР(1,2,3) = 2, нагрузка «Y-0»коммутация ключей без пауз'
Масштаб тока-1.
Масштаб напряжения-1.
Масштаб времени-1.
Имя KT-3FTETR
BLOCK E1;
'Общий силовой блок питания инвертора'
EP NY=1,0 BX1=X,PSEP,I1;
LP1 L=0.01E-3 NY=1,2;
LP2 L=0.01E-3 NY=1,22;
CP1 C=100.E-3 NY=2,0 U=2.35;
CP2 C=100.E-3 NY=22,0 U=2.35;
'Косоугольная матрица взаимоиндуктивностей 3-х фазной системы'
LMF11 M=0.5E-3 NY=2,31;
LMF21 M=0.49998E-3,0.5E-3 NY=51,22;
LMF12 M=0,0,0.5E-3 NY=2,32;
LMF22 M=0,0,0.49998E-3,0.5E-3 NY=52,22;
LMF13 M=0,0,0,0,0.5E-3 NY=2,33;
LMF23 M=0,0,0,0,0.49998E-3,0.5E-3 NY=53,22;
LM11 M=0,0,0,0,0,0,20.E-3 NY=31,41;
LM21 M=0,0,0,0,0,0,19.9998E-3,20.E-3 NY=61,51;
LM31 M=0,0,0,0,0,0,39.9998E-3,39.9998E-3,80.E-3 NY=71,8;
LM12 M=0,0,0,0,0,0,0,0,0,20.E-3 NY=32,42;
LM22 M=0,0,0,0,0,0,0,0,0,19.9998E-3,20.E-3 NY=62,52;
LM32 M=0,0,0,0,0,0,0,0,0,39.9998E-3,39.9998E-3,80.E-3 NY=72,8;
LM13 M=0,0,0,0,0,0,0,0,0,0,0,0,20.E-3 NY=33,43;
LM23 M=0,0,0,0,0,0,0,0,0,0,0,0,19.9998E-3,20.E-3 NY=63,53;
LM33 M=0,0,0,0,0,0,0,0,0,0,0,0,39.9998E-3,39.9998E-3,80.E-3 NY=73,8;
'Блок фазы 1'
CF1 C=0.24E-3 NY=71,8;
RH1 R=4. NY=71,8;
KT11 NY=41,0 S=7;
V11 NY=0,41 S=7;
KT21 NY=61,0 S=7;
V21 NY=0,61 S=7;
'Блок фазы 2'
CF2 C=0.24E-3 NY=72,8;
RH2 R=4. NY=72,8;
KT12 NY=42,0 S=7;
V12 NY=0,42 S=7;
KT22 NY=62,0 S=7;
V22 NY=0,62 S=7;
'Блок фазы 3'
CF3 C=0.24E-3 NY=73,8;
RH3 R=4. NY=73,8;
KT13 NY=43,0 S=7;
V13 NY=0,43 S=7;
KT23 NY=63,0 S=7;
V23 NY=0,63 S=7;
END E1;
BLOCK I1;
'Блок управляющих источников'
PSEP K1=2.35;
SINZ1-1 K1=3.1 TF=0.0 TP=20.E-3;
SINZ2-1 K1=3.1 TF=6.667E-3 TP=20.E-3;
SINZ3-1 K1=3.1 TF=-6.667E-3 TP=20.E-3;
END I1;
BLOCK F1;
'Система управления фазой 1'
YCI1 K1=1. K2=-1. BX1=I,KT11,E1 BX2=I,KT21,E1;
YCS1 K1=1. K2=-1. BX1=U,KT11,E1 BX2=U,KT21,E1;
AZ11-1 KU=1. TP=0.7E-3 BX1=X,YCS1 X=0.;
AZ21-1 KU=1. TP=0.7E-3 BX1=X,AZ11 X=0.;
AK11-2 BX1=X,AZ11 BX3=S,OR11;
AK21-2 BX1=X,AZ21 BX3=S,OR11;
YC11 K1=-0.0644 K2=-1.02 K3=-0.9356 BX1=X,YCS1 BX2=I,CF1,E1 BX3=U,CF1,E1;
YC21 K1=1. K2=1. BX1=X,YC11 BX2=X,SINZ1,I1;
KM11-0 K1=1. BX1=X,AZ21 BX2=X,YC21 S=0;
NOT11 BX1=S,KM11 S=1;
OB11 TI=4.E-6 BX1=S,KM11 S=0;
OB21 TI=4.E-6 BX1=S,NOT11 S=0;
OR11 BX1=S,OB11 BX2=S,OB21 S=0;
'Блок логических автоматов диодов и ключей фазы 1'
AKCKT11-9 BX1=S,KT11,E1 BX2=S,KM11;
AKCKT21-9 BX1=S,KT21,E1 BX2=S,NOT11;
KMUIV11-0 K1=1. BX1=2,V11,E1 BX2=1,V11,E1;
KMUIV21-0 K1=1. BX1=2,V21,E1 BX2=1,V21,E1;
ADV11-9 BX1=S,V11,E1 BX2=1,KMUIV11;
ADV21-9 BX1=S,V21,E1 BX2=1,KMUIV21;
' Система управления фазой 2'
YCI2 K1=1. K2=-1. BX1=I,KT12,E1 BX2=I,KT22,E1;
YCS2 K1=1. K2=-1. BX1=U,KT12,E1 BX2=U,KT22,E1;
AZ12-1 KU=1. TP=0.7E-3 BX1=X,YCS2 X=0.;
AZ22-1 KU=1. TP=0.7E-3 BX1=X,AZ12 X=0.;
AK12-2 BX1=X,AZ12 BX3=S,OR12;
AK22-2 BX1=X,AZ22 BX3=S,OR12;
YC12 K1=-0.0644 K2=-1.02 K3=-0.9356 BX1=X,YCS2 BX2=I,CF2,E1 BX3=U,CF2,E1;
YC22 K1=1. K2=1. BX1=X,YC12 BX2=X,SINZ2,I1;
KM12-0 K1=1. BX1=X,AZ22 BX2=X,YC22 S=0;
NOT12 BX1=S,KM12 S=1;
OB12 TI=4.E-6 BX1=S,KM12 S=0;
OB22 TI=4.E-6 BX1=S,NOT12 S=0;
OR12 BX1=S,OB12 BX2=S,OB22 S=0;
' Блок логических автоматов диодов и ключей фазы 2'
AKCKT12-9 BX1=S,KT12,E1 BX2=S,KM12;
AKCKT22-9 BX1=S,KT22,E1 BX2=S,NOT12;
KMUIV12-0 K1=1. BX1=2,V12,E1 BX2=1,V12,E1;
KMUIV22-0 K1=1. BX1=2,V22,E1 BX2=1,V22,E1;
ADV12-9 BX1=S,V12,E1 BX2=1,KMUIV12;
ADV22-9 BX1=S,V22,E1 BX2=1,KMUIV22;
' Система управления фазой 3'
YCI3 K1=1. K2=-1. BX1=I,KT13,E1 BX2=I,KT23,E1;
YCS3 K1=1. K2=-1. BX1=U,KT13,E1 BX2=U,KT23,E1;
AZ13-1 KU=1. TP=0.7E-3 BX1=X,YCS3 X=0.;
AZ23-1 KU=1. TP=0.7E-3 BX1=X,AZ13 X=0.;
AK13-2 BX1=X,AZ13 BX3=S,OR13;
AK23-2 BX1=X,AZ23 BX3=S,OR13;
YC13 K1=-0.0644 K2=-1.02 K3=-0.9356 BX1=X,YCS3 BX2=I,CF3,E1 BX3=U,CF3,E1;
YC23 K1=1. K2=1. BX1=X,YC13 BX2=X,SINZ3,I1;
KM13-0 K1=1. BX1=X,AZ23 BX2=X,YC23 S=0;
NOT13 BX1=S,KM13 S=1;
OB13 TI=4.E-6 BX1=S,KM13 S=0;
OB23 TI=4.E-6 BX1=S,NOT13 S=0;
OR13 BX1=S,OB13 BX2=S,OB23 S=0;
' Блок логических автоматов диодов и ключей фазы 3'
AKCKT13-9 BX1=S,KT13,E1 BX2=S,KM13;
AKCKT23-9 BX1=S,KT23,E1 BX2=S,NOT13;
KMUIV13-0 K1=1. BX1=2,V13,E1 BX2=1,V13,E1;
KMUIV23-0 K1=1. BX1=2,V23,E1 BX2=1,V23,E1;
ADV13-9 BX1=S,V13,E1 BX2=1,KMUIV13;
ADV23-9 BX1=S,V23,E1 BX2=1,KMUIV23;
END F1;
&&&&&&
&&&&&
VII. Выходные напряжения при пуске и различных режимах работы модели.
1. Bыходные напряжения при работе модели 3-фазного тетра-инвертора с раздельными фазными магнитносвязанными дросселями и с раздельными фазными трансформаторами, каждый с коэффициентом трансформации NТР1 = NТР2 = NТР3 = 2, в номинальном и предельных режимах, представлены на рис 8.
2. Для фазы «1», синусоидальное задание
е(1)^ по напряжению с нормированной амплитудой К11 = 3.1[В, ампл], нулевым фазовым сдвигом TI1 = 0.0 [сек] и с периодом TP1 = 20·10−3 [сек].
3. Для фазы «2», синусоидальное задание
е(2)^ по напряжению с нормированной амплитудой К12 = 3.1[В], положительным фазовым сдвигом TI2 = +6.67·10−3 = [сек] и с периодом TP2 = 20·10−3 [сек].
4. Для фазы «3», синусоидальное задание
е(3)^ по напряжению с нормированной амплитудой К13 = 3.1[В], отрицательным фазовым сдвигом TI3 = − 6.67·10−3 = [сек] и с периодом TP3 = 20·10−3 [сек].
5. URH1 = URH2 = URH3 – Сформированные тетра-инвертором, почти «гладкие» синусоиды симметричных фазных выходных напряжений на номинальной нагрузке, включенной звездой с нулём «Y-0», при RH1 = = RH2 = RH3 = 4 [Ом].
6. При работе инвертора происходит непрерывное произведение постоянного напряжения питания U на обобщённую коммутационную функцию Si = sign [+1, −1], в каждой фазе, т.е. импульсное питание инвертора равно: ±ui = Si·U, при i = 1, 2, 3. Одновременно с этим, по передним фронтам этих коммутационных функций, соответствующими драйверами с гальванической развязкой, в каждой фазе формируются сигналы управления парами силовых ключей ветвей фазы инвертора.
7. Шаг прогноза для каждой фазы: hi = TP1 = TP2 = 0.7·10−3 [сек]. Частота модуляции в каждой фазе определяется по своему шагу прогноза: fi.MOD =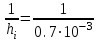 = 1.43·103 [Гц], при i = 1, 2, 3. = 1.43·103 [Гц], при i = 1, 2, 3.
8. На рис 8. представлен пуск и работа трёхфазного тетра-инвертора при постоянном питании ветвей инвертора UP1 = UP2 = 2.35[B], с симметричным выходным фазным почти синусоидальным напряжением
URH1 = URH2 = URH3 = 3.1[B, ампл], нагрузка инвертора номинальная и включена звездой с нулём «Y-0», при RH1 = RH2 = RH = 4[Ом].
9. На рис 9. представлен пуск и работа трёхфазного тетра-инвертора при постоянном питании ветвей инвертора UP1 = UP2 = 2.35[B], с симметричным выходным линейным почти синусоидальным напряжением
URH1 = URH2 = URH3 =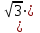 3.1 ≈ 5.4[B, ампл], нагрузка инвертора номинальная и включена в треугольник «∆», при RH1 = RH2 = RH3 = = 3.1 ≈ 5.4[B, ампл], нагрузка инвертора номинальная и включена в треугольник «∆», при RH1 = RH2 = RH3 = =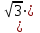 4 ≈ 7 [Ом]. 4 ≈ 7 [Ом].

Рис 8. Пуск и работа 3-х фазного тетра-инвертора с фазными дросселями и трансформаторами с NTPi = 2, нагрузка «Y-0».
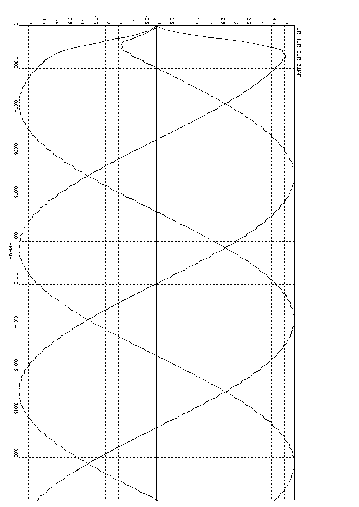
Рис 9. Пуск и работа 3-х фазного тетра-инвертора с фазными дросселями и трансформаторами с NTPi = 2, нагрузка «∆».
Заключение.
1. Управления по вычисляемому прогнозу обеспечивает отслеживание выходного параметра при минимальной кратности частот модуляции и задания, что позволяет реализовать преобразователи на большие мощности. Применение тетра-инвертора с вычислителем, снижает коммутационные потери в силовых ключах, и уменьшает количество и размеры их охладителей, и размеры всей конструкции. Достигается улучшение эксплуатационных характеристик: коэффициент несинусоидальности выходного напряжения, КПД, при работе с комплексной нагрузкой, как с линейной, так и с нелинейной. Улучшается качество электроэнергии в переходных процессах при переключениях и «набросах» нагрузки. Это снижает массогабаритные показатели и стоимость элементов фильтра, позволяет использовать преобразователь меньшей мощности с устойчивой работой на нелинейную нагрузку.
2. Полученные расчётные соотношения для силовых элементов следящих и стабилизированных однофазных и трёхфазных моделей тетра-инверторов и их систем управления, необходимые параметры, коэффициенты усиления и постоянные времени вычислителей условного прогноза. Они были проверены и уточнены с помощью программ машинного анализа силовой электроники "ELTRAN".
Список литературы.
1. Отто Дж. М. Смит Автоматическое регулирование. Пер. с англ. Под редакцией Е.П. Попова. Государственное издательство физико − математической литературы. Москва, 1962, стр.: 330, 698, 776.
2. Мустафа Г.М. Расчёт импульсно – модулированных инверторов с синусоидальным выходным напряжением. Электротехника, №2, 1988. |
 Скачать 360.87 Kb.
Скачать 360.87 Kb.
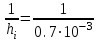 = 1.43·103 [Гц], при i = 1, 2, 3.
= 1.43·103 [Гц], при i = 1, 2, 3.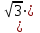 3.1 ≈ 5.4[B, ампл], нагрузка инвертора номинальная и включена в треугольник «∆», при RH1 = RH2 = RH3 = =
3.1 ≈ 5.4[B, ампл], нагрузка инвертора номинальная и включена в треугольник «∆», при RH1 = RH2 = RH3 = =
