Тервер 00. Тическая статистика (специальные главы) основы случайных процессов
 Скачать 198.27 Kb. Скачать 198.27 Kb.
|
|
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ Контрольная работа ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА (специальные главы) ОСНОВЫ СЛУЧАЙНЫХ ПРОЦЕССОв Выполнил: Решенина И. И. Факультет ЗФ, группа БРС1251 Москва 2014 г. Вариант 00 Задание 1. Задан случайный процесс: Х(t) = u (t3 + 5). Найти математическое ожидание ковариационную функцию и дисперсию случайных процессов: 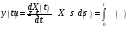 , ,где u - случайная величина с известной плотностью распределения: 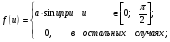 k=3, m=5 Р е ш е н и е: Найдем параметр а из условия: 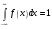 . .Потребуем, что бы это условие выполнялось для заданной функции: 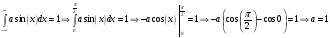 Тогда плотность распределения будет иметь вид: 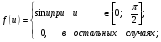
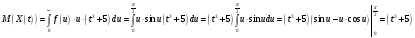 Используя свойство дифференцирования и интегрирования случайных процессов получим, что: 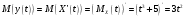 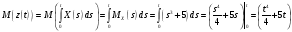
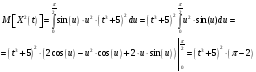 Тогда дисперсия равна: 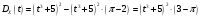
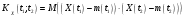 Предварительно найдём: 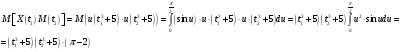 Тогда: 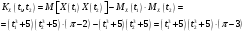 Используя свойство дифференцирования и интегрирования случайных процессов получим, что: 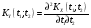 - равна второй смешанной производной. - равна второй смешанной производной.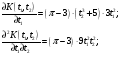 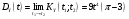 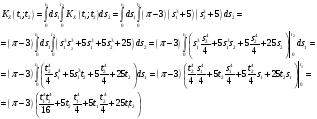 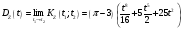 Задание 2. На вход сглаживающего фильтра (см. рис.) подаётся "белый" шум, имеющий спектральную плотность S0= 100(мкв)2/Гц. Для данной схемы R = 103кОм, L = m*10-3Гн, где m = 3. Найти:
При вычислениях воспользоваться формулой: 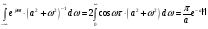 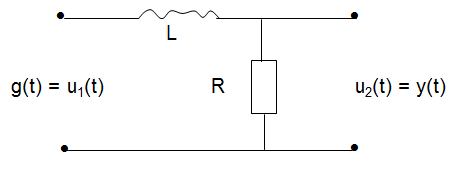 Р е ш е н и е: Дифференциальное уравнение, описывающее связь между входным и выходным напряжением LR - цепочки, имеет вид: 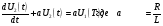 – апериодическое звено. – апериодическое звено.Апериодические звенья относятся по классификации к позиционным звеньям. Апериодическое звено - это звено, которое описывается следующим дифференциальным уравнением (учитывается демпфирование): 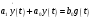 . .
k = 1– статистический коэффициент усиления безынерционного звена. Решение данного Д.У. 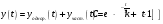 , если у(0) = 0 и t = 0, то , если у(0) = 0 и t = 0, то 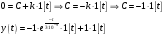
Передаточная функция апериодического звена: Передаточной функцией звена называется комплексный коэффициент, связывающий изображение входного и выходного сигнала при нулевых начальных условиях. Передаточной функцией звена называется отношение Лапласа выходной к входной величин, т.е. 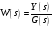 при нулевых начальных условиях. при нулевых начальных условиях.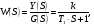 а преобразования входного сигнала 1(t) имеет вид: а преобразования входного сигнала 1(t) имеет вид: 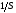 . Подставляя вместо S =jω, получим комплексную передаточную функцию: . Подставляя вместо S =jω, получим комплексную передаточную функцию: 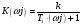 . .
Спектральная плотность SX(ω) для заданной ковариационной функции равна: 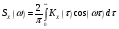 . . 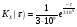 . Так как . Так как 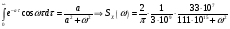 SХ(0) = 100(мкв)2/Гц. = 100*10-12 (в)2/Гц 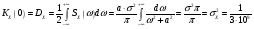 . .Задание 3. На вход линейной динамической системы, описываемой дифференциальным уравнением: 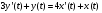 подаётся стационарный случайный процесс x(t) с ковариационной функцией подаётся стационарный случайный процесс x(t) с ковариационной функцией 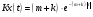 . .Если m + k = m*k = 0, то считать m = 7, k = 3. Получаем: 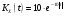 . Найти дисперсию случайного процесса на выходе из системы в установившемся режиме. . Найти дисперсию случайного процесса на выходе из системы в установившемся режиме.Р е ш е н и е: Вычисляя преобразование Лапласа от обеих частей при начальных условиях, получим формулу для передаточной функции линейной системы: 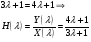 Подставляя вместо λ =jω, найдём амплитудночастотную характеристику системы: 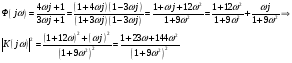 Спектральная плотность SX(ω) для заданной ковариационной функции равна: 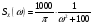 . .Найдём спектральную плотность с.п. на выходе системы: 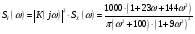 Дисперсия случайной величины y(t) находим по формуле: 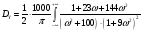 , где несобственный интеграл: , где несобственный интеграл: 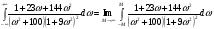 Рассмотрим неопределенный интеграл: 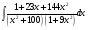 Разложим подынтегральную дробь на сумму простейших дробей: 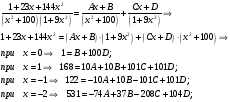 Получаем систему: 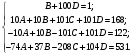 Решим эту систему методом Крамера: 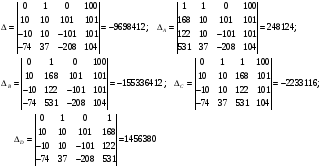 Далее находим коэффициенты: 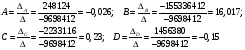 Получаем интеграл: 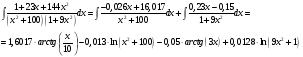 Далее возвращаемся к определённому интегралу: 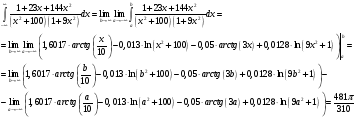 Окончательно получаем: 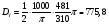 . .Задание 4. Цепь Маркова с тремя состояниями S1, S2, S3 характеризуется однородной стохастической матрицей: 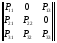 (m =2) (m =2)где: Р11 = Р22 = Р33 = m/(m+2) = 0,5; P13 = P21 = 2/(m + 2) = 0,5; P31 =P32 =1/(m + 2) = 0,25. Требуется:
Р е ш е н и е: Имеем матрицу: 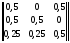
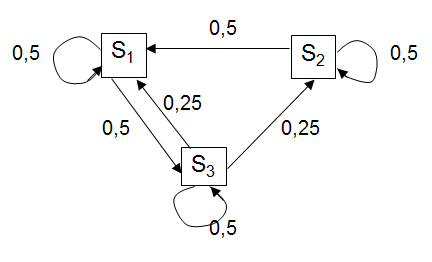
То есть Р1(0) = 1, Р2(0) = Р3(0) = 0; Р11 = Р22 = Р33 = 0,5; Р13 = Р21 = 0,5; Р12 = Р23 = 0; Р31 = Р32 = 0,25. Тогда: 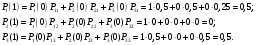 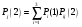 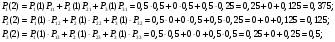 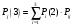 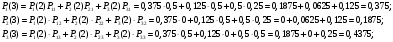 Следовательно: Р1(3) = 0,375; Р2(3) = 0,1875; Р3(3) = 0,4375. |

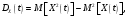 где:
где: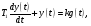 где: T1 = 3*10-9,
где: T1 = 3*10-9,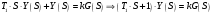
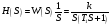 . Разложив на элементарные дроби правую часть последнего выражения получим:
. Разложив на элементарные дроби правую часть последнего выражения получим: 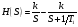 и,
и, 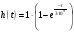 . Продифференцировав это уравнение, получим импульсно-переходную функцию:
. Продифференцировав это уравнение, получим импульсно-переходную функцию: 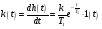 . Подставляя коэффициенты своего уравнения получим импульсно-переходную функцию:
. Подставляя коэффициенты своего уравнения получим импульсно-переходную функцию: 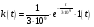 .
.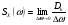 .
.