|
|
Урок геометрии Теорема Пифагора. разработка урока 8 класс. Теорема Пифагора. Тип урока урок открытия новых знаний, обретения новых умений и навыков. Дата урока 28. 01. 2020г. Тема урока Теорема Пифагора Цели Развивающие
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ОТКРЫТОГО УРОКА С ИСПОЛЬЗОВАНИЕМ СИСТЕМНО - ДЕЯТЕЛЬНОСТНОГО ПОДХОДА
Учитель: Зотова Татьяна Васильевна, учитель математике, МКОУ – Новопичуговской СОШ
Предмет: Геометрия
Тип урока: урок открытия новых знаний, обретения новых умений и навыков.
Дата урока: 28.01.2020г.
Тема урока: «Теорема Пифагора»
Цели:
Развивающие:
создать условия, в которых учащиеся могли бы самостоятельно планировать и анализировать собственные действия, находить выход из любой ситуации, реально оценивать свои возможности и знания.
Воспитательные:
воспитывать познавательный интерес к предмету, любовь к поисковым решениям, культуру поведения при фронтальной, групповой и индивидуальной работе.
Образовательные:
ознакомить и обеспечить овладение учащимися основными алгоритмическими приемами при нахождении сторон прямоугольного треугольника при помощи теоремы Пифагора; показать практическое применение теоремы Пифагора в жизни;
способствовать развитиюматематической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
Основные термины и понятия: доказательство теоремы Пифагора алгебраическим методом и демонстрацией площади составной фигуры; решение задач на нахождение гипотенузы по известным катетам; решение задач на нахождение катета по известному катету и гипотенузе.
Планируемые результаты
|
Предметные
|
Универсальные учебные действия
|
уметь доказывать теорему Пифагора, указанным методом;
уметь находить неизвестные элементы прямоугольных треугольников по известным;
уметь устанавливать логические отношения между данными и искомыми;
использовать для решения геометрических задач графические модели в соответствии с содержанием задания.
|
Познавательные УУД: уметь ориентироваться в своей системе знаний:отличать новое от уже известного с помощью учителя;добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Коммуникативные УУД: уметь оформлять свои мысли в устной форме;слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
Регулятивные УУД: уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.
Личностные УУД: способность к самооценке на основе критерия успешности учебной деятельности.
|
Формы работы
|
Фронтальная (Ф), индивидуальная (И), Самостоятельная (С)
|
Образовательные ресурсы
|
учебник для общеобразовательных учреждений : «Геометрия 7-9 класс» Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.; методическое пособие;
ЭОР;
презентация к уроку;
наглядный и раздаточный материал.
|
№
|
Этап урока
|
Содержание педагогического взаимодействия
|
Формирование УУД
|
Деятельность учителя
|
Деятельность учащихся
|
1.
|
Организационно-мотивационный этап.
(5 мин)
|
Приветствие учащихся, проверяет готовность учащихся к уроку. Мотивирует учащихся на восприятие нового материала:
- Сегодня у нас с вами необычный день и необычный урок. Какие дни для себя вы считаете необычными?
- А какие уроки вы считаете необычными?
- А что необычное вы заметили сегодня в классе?
- Прочитайте их и выберите три наиболее вам подходящие.
- А кто такой - Пифагор? Где вы раньше слышали это имя?
Значит, Пифагор имеет отношение к математике, и наш урок необычен тем, что мы сегодня не только изучим одну из самых известных геометрических теорем древности, называемую теоремой Пифагора, но и познакомимся с древнегреческим учёным Пифагором Самосским. Кто же такой Пифагор?
- Ответить на этот вопрос мне поможете ученик со своим домашним заданием.
- Подведем итог, кто же такой Пифагор?
Пифагорейцами было сделано много важных открытий в арифметики и геометрии. Например, известная нам теорема о сумме углов треугольника, теорема о соотношении сторон в прямоугольном треугольнике.
|
Приветствуют учителя, настраиваются на урок
Ответы учащихся:
дни рождения, семейные праздники, дни, когда, происходят события, значимые для вас.
Нестандартные уроки, когда узнаём что-то очень интересное.
На экране заповеди Пифагора.
Презентация (слад 1)
Учащиеся высказывают свое мнение.
Называют таблицу Пифагора, портрет Пифагора в кабинете математики.
Демонстрирует презентацию и рассказывает о Пифагоре Самосском.
Ученики воспринимают информацию.
Учёный, мыслитель, философ, поборник нравственности, поклонник ЗОЖ.
|
Личностные: самоопределение.
Регулятивные: целеполагание.
Коммуникативные: планирование сотрудничества с учителем и сверстников
|
2.
|
Актуализация знаний.
( 7 мин)
|
Подготовка к изучению нового материала, повторяется тот материал, который нужен будет при доказательстве теоремы.
Вопросы:
- Как вычислить площадь квадрата?
-Чему равна площадь квадрата, если его сторона равна 4 см, с см, (а+в) см?
-Какой треугольник называется прямоугольным?
-Как называются стороны прямоугольного треугольника?
-Назовите катеты и гипотенузу прямоугольного треугольника АВС с прямым углом С.
-Как вычислить площадь прямоугольного треугольника?
Решение задач:
Презентация: Слайды 2, 3, 4
1.Чему равна площадь прямоугольного треугольника с катетами 6 см и 7 см?
2.Площадь прямоугольного треугольника равна 20 см2, один из катетов 5 см. Найдите неизвестный катет.
3.По данным на рисунке найдите площадь треугольника АВС, если  А=600, АВ = 14, ВС = 8. А=600, АВ = 14, ВС = 8.
А
С В
|
Учащиеся дают ответы на поставленные вопросы.
Устанавливают логические отношения между данными и искомыми величинами
Решают устно задачи: №1, №2, №3.
Выбирают способ решения задачи.
|
Предметные: установление логических связей между данными и искомыми величинами, использование для решения геометрических задач графических моделей.
Познавательные: анализ задачи с целью выявления существенных признаков, выбор эффективного способа решения, контроль и оценка результатов деятельности.
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, опираясь на определения и теоремы.
|
3.
|
Постановка учебной задачи.
(3 мин.)
|
Создает проблемную ситуацию:
Задача. Презентация: Слайд 5
Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты.
Хватит ли 50 м троса для крепления мачты
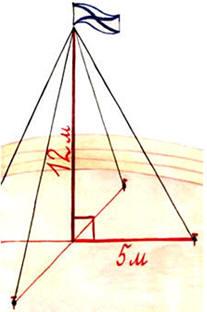
Зависимость между сторонами в прямоугольном треугольнике была доказана Пифагором, поэтому эта теорема носит его имя.
- Попробуйте сформулировать тему урока
- В тетрадях запишите число и тему урока.
|
Выдвигаются версии, какую формулу применить при ответе на вопрос. Фиксируется затруднение в деятельности.
Перед учащимися возникает проблема: как найти длину одного троса.
Участвуют в формулировке темы урока и постановке целей.
|
Регулятивные: целеполагание.
Познавательные: самостоятельное выделение и формулирование проблемы.
|
4.
|
Построение проекта выхода из затруднения.
(9 мин)
|
Учитель организует практическую работу.
Раздает разноцветные фигуры по группам (прямоугольные треугольники со сторонами a,b, c)
 
Вопросы к практической работе.
1.Установите связь между гипотенузой и катетами, пользуясь моделями фигур
2.Можно ли увидеть закономерность между длинами катетов и гипотенузы?
Учитель выслушивает ответы у каждой группы и задает вопросы.
Зависимость, которую мы с вами установили, в геометрии называют теоремой Пифагора.
Учитель совместно с учащимися формулируют цель урока.
Записывают тему урока. Презентация: Слайды 6.
Попробуйте сами сформулировать теорему Пифагора.
Корректирует формулировку, данную учениками, советует сравнить ее с формулировкой в учебнике на странице 130, обращая внимание на то, что теорема свойственна только для прямоугольных треугольников.
Теорема Пифагора выражает зависимость между гипотенузой и катетами прямоугольного треугольника.
А теперь попытаемся доказать теорему Пифагора.
Рассмотрим доказательство теоремы Пифагора
Запускает и демонстрирует ЭОР.
(Виртуальная школа Кирилла и Мефодия. Уроки геометрии. 8 класс.)
- Каждую часть сначала прослушивают, а затем конспектируют в тетрадь (если что- то не понятно учитель комментирует по ходу).
|
Учащиеся выполняют практическую работу
Учащиеся формулируют теорему.
Анализируют, насколько правильно была составлена ими формулировка, сравнив ее с формулировкой, найденной в тексте учебника
Оформляют в тетрадях чертеж и записывают дано.
Делают необходимые записи в тетрадь.
После записи доказательства один из «сильных» учащихся пробует сам без звука и текста воспроизвести доказательство теоремы Пифагора.
|
Предметные: умение выводить формулу для вычисления площади прямоугольного треугольника
Метапредметные: использование алгебраических преобразований.
Регулятивные: планирование,
Прогнозирование, сопоставление результатов преобразований
Познавательные: моделирование ситуации, построение логической цепи рассуждений, выдвижение гипотез и их обоснование,
Доказательство теоремы.
Коммуникативные: сотрудничество в поиске и выборе способа решения возникшей проблемы.
|
5.
|
Первичное закрепление новых знаний.
(6 мин.)
|
-Теперь, зная зависимость между катетами и гипотенузой в прямоугольном треугольнике, ответим на вопрос. Хватит ли 50 м троса для крепления мачты.
Презентация: Слайд 5
Предлагает учащимся ознакомиться с иными формулировками теоремы Пифагора. Запускает ЭОР.
-Многие писатели прошлого обращались к этой замечательной теореме и посвящали ей свои строки.
Презентация: Слайд 7
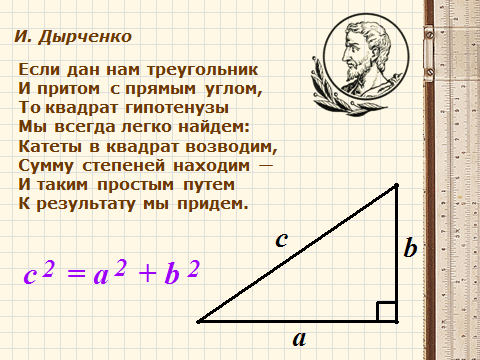
Устанавливает осознанность восприятия учебного материала.
Рассматривается решение типовых задач из учебника.
|
У доски сильный ученик решают задачу с пояснением, все остальные учащиеся работают в тетрадях.
На основании решения делают вывод (как найти гипотенузу, зная два катета и как найти катет, зная гипотенузу и катет).
Воспринимают информацию, сравнивают формулировки.
Читают стихотворение.
Решают типовые задачи:
Работа по учебнику (Применение теоремы Пифагора к решению задач).
Задачи решаются на доске и в тетрадях.
№ 483 (б),
№ 484 (а).
|
Предметные: умения устанавливать логические отношения между данными и искомыми, использовать для решения геометрических задач графические модели в соответствии с содержанием задания.
Познавательные: умение структурировать знания, выбирать способы решения задач, умение строить речевое высказывание, рефлексия способов и условий действия.
Регулятивные: контроль, оценка, коррекция.
Коммуникативные: управление поведением партнёра – контроль, коррекция, оценка действий партнёра.
|
6.
|
Контроль и оценка результатов деятельности.
(6 мин,)
|
Организует деятельность по контролю усвоения приобретенных знаний.
|
Выполняют проверочную самостоятельную работу.
1. Найти гипотенузу прямоугольного треугольника, если известны катеты.
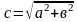
2. Найти катет, если известна гипотенуза и другой катет.
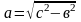
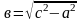
|
Личностные: самоопределение. Регулятивные: контроль, коррекция.
|
7.
|
Домашнее задание
(2 мин.)
|
Объясняет домашнее задание.
Презентация: Слайд 8
п.54 №483(б, г), №484(а). Инструктирует по выполнению заданий.
Презентация: Слайд 9
Творческое задание:
- Существует более 100 способов доказательства теоремы. Найдите другие способы доказательства этой теоремы.
- Найдите ответ на вопрос: «Почему теорему Пифагора называют теоремой пчёлки или теоремой невесты?»
|
Записывают домашнее задание в дневники.
|
Личностные: смыслообразование.
Познавательные: рефлексия
Коммуникативные: умение с
достаточной полнотой и
точностью выражать свои мысли.
|
8.
|
Рефлексия деятельности.
(2 мин.)
|
Организует рефлексию
- Чем необычный был для вас сегодняшний урок?
- Что нового и интересного вы узнали на уроке?
- Что научились делать?
Презентация: Слайд 9
- Организует рефлексию и самооценку учениками собственной учебной деятельности предлагаются следующие фразы:
|
Отвечают, на вопросы с аргументацией, оценивают свою работу на уроке.
Продолжают фразы.
Самооценивание
|
Познавательные: Способность к самооценке на основе критерия успешности учебной деятельности;
Коммуникативные: Уметь критически относится к себе и к своим знаниям
|
 |
|
|
 Скачать 431.09 Kb.
Скачать 431.09 Kb.





