Блок-схемы Телегина НО-1703.z. Цель установить отношения между данными и искомыми числами задачи
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
    Методически принято выделять следующие этапы работы над задачей на уроке:     ЦЕЛЬ: установить отношения между данными и искомыми числами задачи. Моделирование – это процесс построения моделей для каких-либо познавательных целей. В процессе решения задачи ученик не может непосредственно исследовать ту ситуацию, которая предлагается ему в тексте задачи. Смысл же решения задачи состоит в том, чтобы описать данную в тексте ситуацию с помощью математических символов, для этого необходимо выделить количественные характеристики описанной ситуации и тип связей между ними. В математике модели делятся на схематизированные и словесно-графические. В свою очередь, схематизированные модели бывают вещественными (они обеспечивают физическое действие с предметами, инсценировка, представление) и графическими (они обеспечивают графическое действие – рисунок, условный рисунок, схематический чертеж, схема). Словесно-графическая модель задачи может выполняться как на естественном языке (в виде краткой записи, таблицы), так и на математическом, когда используются математические символы Моделирование текста задачи. Усвоение содержания задачи.   Виды моделей, применяемых при решении текстовых задач:  ЦЕЛЬ: представить ситуацию, описанную в задаче; понять задачу, т.е. выделить объекты или величины, используемые в задаче, установить их числовые данные, отделить известные данные от неизвестных, определить отношения между ними. Данный этап состоит из нескольких моментов: а) Чтение задачи. При чтении задачи необходимо выделять голосом числа, используемые в задаче, отношения между объектами и, конечно, требование. Перед чтением вслух, ученики должны прочитать задачу «про себя». Задачу ученики всегда читают самостоятельно, в исключительных случаях (букварный период, задача нового вида) читает учитель. Вслух задачу полезно читать один раз. Повторное (выборочное) чтение можно осуществлять в процессе повторения задачи. б) Повторение задачи. Приемы повторения: 1. Абстрагирование к виду числа. 2. Повторение задачи по логическим частям. 3. Повторение задачи по структурным частям. 4. Повторение полного текста задачи.         3. Таблица. Этот вид модели похож на краткую запись, но данные расставляются не по строкам к опорным словам, а структурируются в таблицу. Наиболее удачно применение таблицы при решении задач на тройку пропорциональных величин: 2. Краткая запись - представление в лаконичной форме содержания задачи, выполненное с помощью опорных слов, простых математических выражений, значения исходных величин, связей между ними, а также данными и искомыми величинами. Это наиболее распространенный путь облегчения учащимся перехода от словесной модели к представлению ситуации, описанной в задаче. 1. Рисунок - изображает реальные предметы, о которых говорится в задаче, или условные предметы в виде геометрических фигур.    4. Чертеж - условное изображение предметов, взаимосвязей между ними и взаимоотношения величин с помощью отрезков и с соблюдением определенного масштаба. Чертеж как вид модели целесообразно применять при следующих условиях: наличие у детей определенных навыков вычерчивания отрезков заданной длины; удобные числовые данные в задаче, позволяющие начертить отрезок заданной длины. 5. Схема - это чертеж, на котором все взаимосвязи и взаимоотношения величин передаются приблизительно, без соблюдения масштаба. Схема является наиболее предпочтительной моделью при решении задач по ряду причин: она исключает пересчет (как и чертеж); может быть использована при решении задач со сколь угодно большими числами; может применяться при решении задач с буквами; достаточно конкретна, и полностью отражает внутренние связи и количественные отношения в задаче; позволяет подняться на достаточно высокую ступень абстрактности: не отражает никаких отношений, кроме количественных; все второстепенные детали опущены; выбор действия производится без учета главного (опорного) слова, а только исходя из логики происходящих изменений, которые отражены в модели; внешняя схожесть схем подчеркивает однотипность рассуждений при поиске решения задач; способствует формированию общего способа действия в задачах одного типа. 6. Блок-схема. Этот вид модели еще называют «дерево рассуждений». Некоторые методисты не выделяют блок-схему как отдельную модель. На наш взгляд, это неверно, так как при составлении модели в виде блок-схемы используются приемы, отличающиеся от приемов составления моделей других видов: 1) при построении данной модели используется разбор задачи начиная с вопроса; 2) в блок-схеме нет опорных слов, на которые можно ориентироваться при выборе действия (как в краткой записи); 3) отсутствует зрительный ориентир для сравнения величин между собой (как при работе со схемой и чертежом); 4) ребенок ориентируется только на взаимоотношения и взаимосвязи, описанные в задаче. Составление блок-схемы сопровождается обязательным поэтапным анализом. Словесно-графическая модель задачи может выполняться как на естественном языке (в виде краткой записи, таблицы), так и на математическом, когда используются математические символы
   ЦЕЛЬ: реализовать план, т.е. записать решение задачи. Решение задачи сводится к записи ее символической модели.   Решая задачу арифметическим методом символическая модель может быть представлена: 1) действиями без пояснения; 2) действиями с пояснением; 3) в виде составного выражения с последующим вычислением его значения; 4) планом и последующим решением задачи по действиям. (Планом называют последовательность вопросов, отвечая на которые мы приходим к ответу на вопрос задачи); 5) вопросами и записью действий, с помощью которых можно ответить на каждый вопрос. Решая задачу алгебраическим методом, символическая модель может быть представлена: а) в виде уравнения и его решения; б) через запись шагов составления уравнения, самого уравнения и его решения. ЦЕЛЬ: убедиться в истинности выбранного плана решения и выполненных действий. Выделяются следующие способы проверки правильности решения задачи:  ЦЕЛЬ: выбрать метод решения и составить план решения задачи. В математике различают следующие методы решения арифметических задач: практический, графический, арифметический и алгебраический. В качестве основных в математике выделяют арифметический и алгебраический методы решения задач. При решении задач арифметическим методом проводится анализ задачи. Выделяется 3 вида анализа задачи: прямой (от данных к вопросу), обратный (от вопроса к данным) и смешанный. В методической литературе прямой анализ задачи принято называть синтетическим, обратный – аналитическим, смешанный - аналитико-синтетическим.    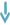       В последнем случае надо проверить правильность выполнения задания, например, предложить учащимся, сидящим за одной партой проговорить вслух вопросы и ответы. Обучение обратному анализу задач начинают с готового решения составной задачи, полученного в ходе прямого анализа. К готовому решению ставят вопросы обратного анализа, обязательно соотнося их с соответствующим действием. В случае применения смешанного анализа используют вопросы того и другого видов анализа. ЦЕЛЬ: развивать у учащихся обобщенные умения, необходимые для решения задач. Данный этап включает в себя следующие виды работы: если решение задачи записывалось по действиям, то можно его записать с помощью составного выражения и вычислить его значение; решение задачи другим способом; варьирование (изменение) данных задачи, а также условия или вопроса; составление обратной задачи. С.Е. Царева [76] рассматривает следующие виды работы с задачами на уроке математики. ЦЕЛЬ: дать ответ на вопрос задачи. Существует 2 формы формулировки ответа: а) формулировка полного ответа на вопрос задачи; б) формулировка краткого ответа на вопрос задачи. Записать ответ можно следующими способами: а) после слова «ответ» ставится точка и тогда сам ответ пишется с заглавной буквы. б) после слова «ответ» ставится двоеточие, и затем сам ответ пишется с маленькой буквы. Приемы обучения прямому анализу: 1. Создание целевой установки на запоминание вопросов анализа (сегодня вопросы к задаче ставлю я, а завтра кто-нибудь из вас.). 2. Ролевая игра: 1) роль учителя выполняет один ученик, остальные - ученики; 2) весь класс выполняет роль учителя, а один ученик – роль ученика; 3) учащиеся первого ряда ставят вопросы классу, а учащиеся второго ряда отвечают на эти вопросы, ученики третьего ряда выступают в роли учителя – следят за правильностью ответов; 4) учащиеся первого варианта задают вопросы учащимся второго варианта. Работа над задачей после ее решения. Запись ответа задачи. 1. Составление и решение одной из обратных задач. Для каждой простой задачи можно составить 2 обратных, т.к. в каждой по 2 известных числа. Для составной – более чем две обратных. 2. Проверка задачи по всем условиям. Этот способ является громоздким, т.к. даже для проверки решения простой задачи требуется выполнить 2 действия. 3. Прогнозирование результата (прикидка, установление границ ответа на вопрос задачи). Рекомендуется применять этот метод при решении простых задач, особенно при нахождении значения суммы и остатка, так как в этих случаях сразу видно правильно решена задача или нет. 4. Решение задачи разными способами (только для составных задач).    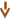              На подготовительном этапе к обучению решению задач необходимо сформировать у учащихся базовые умения: умение слушать и понимать тексты различных структур, умение правильно представлять и моделировать ситуации, предлагаемые учителем, умение правильно выбирать действие в соответствии с ситуацией, умение составлять математическое выражение в соответствии с выбранным действием, умение находить значение математического выражения. Подготовительный этап. Основная задача данного этапа – ознакомлением с понятием «задача» и ее существенными признаками; обучение анализу задачи, формам записи ее решения и ответа; способам проверки правильности решения задачи. В различных системах обучения ознакомление с простой задачей происходит в разное время. В традиционной программе и программе «Школа 2000…» термин «задача» вводится в конце второй четверти, а в системах Л.В. Занкова и «Гармония» учащиеся знакомятся с задачей во втором классе. Для того чтобы деятельность, направленная на усвоение структуры задачи, не была однообразной, не сводилась к восприятию условия и вопроса задачи Н.Б. Истомина предлагает следующие виды упражнений: Сравнение текстов задач. Постановка вопроса учащимися к условию. Составление условия к данному вопросу. Задачи с недостающими данными. Задачи с лишними данными. Преобразование вопроса, условия, данных задачи. Составление задач по рисунку, краткой записи, по решению. Для сравнения целесообразно подбирать такие пары задач, которые имеют: а) одинаковые условия, но различные вопросы; б) одинаковые вопросы, но различия в условиях; в) одинаковые решения, хотя смысл одного и того же действия в каждой задаче различен. их школьников обобщенного умения решения задач. Обобщенное умение решать задачи включает в себя: 1) знание о задачах, методах и способах решения, приемах, помогающих решению в процессе работы над задачей, этапах этого процесса, назначении и содержании каждого этапа; 2) умение расчленять задачи на составные части, использовать различные методы решения, адекватно применять приемы, помогающие понять задачу, составить план решения, выполнить его, проверить решение. С точки зрения методики простая задача является «одношаговым» (А.В. Белошистая) описанием соответствующей ей предметной ситуации. Как было отмечено выше, целью работы над простой задачей является обучение ребенка самостоятельной работе над текстовой формой простой задачи с применением всех приобретенных ранее умений: 1) моделирование заданной в тексте задачи ситуации; 2) выбор арифметического действия и составление математического выражения; 3) вычисление значения составленного выражения; 4) запись ответа задачи; 5) проверка правильности решения задачи. Другими словами, смысл работы над простой задачей заключается в том, что учащиеся в процессе этой деятельности упражняются в применении двух учебных умений: умение перевести текстовое описание ситуации (словесную модель) любого вида в схему (чертеж, краткую запись, предметный рисунок), показывающую взаимосвязь между данными и искомым, и умение оформить эту связь в виде равенства с наименованием (т.е. записать решение, а затем и ответ задачи). формирование у младших школьников обобщенного умения решения задач. |




