Эконометрика Вариант 1 (3 задачи). Титульный лист эконометрика

• Название: Титульный лист эконометрика
• Дата: 13.10.2021
• Размер: 0.51 Mb.
• Имя файла: Эконометрика Вариант 1 (3 задачи).doc
• Тип: Документы; #247045
• страница: 2 из 3

Задание 2

Имеются данные по ряду стран:

Таблица 4

Данные по странам

Страна	Продолжительность жизни при рождении, лет	Численность населения, обслуживаемого одним врачом, чел.	Валовой внутренний продукт на душу населения, тыс. долл.
Россия	65,9	230	9,5
Австрия	77,1	298	24,1
Белоруссия	67,9	230	7,1
Великобритания	77,2	590	21,5
Германия	77,4	295	24,5
Норвегия	78,7	350	29,5
Финляндия	77,2	340	22,4
Франция	78,2	370	25,1
Турция	69,3	820	7,4
Узбекистан	70,3	326	3,5
США	76,9	395	34,3
Япония	81,5	556	31,1

Задание:

1) Определите парные и частные коэффициенты корреляции. Сделайте выводы.

2) Постройте линейное уравнение множественной регрессии и поясните смысл его параметров. Рассчитайте скорректированный коэффициент детерминации.

3) Проверьте значимость уравнения регрессии на 95% уровне.

4) Рассчитайте коэффициенты эластичности. Дайте их интерпретацию

5) Постройте 95% доверительные интервалы для коэффициентов регрессии. Проверьте значимость каждого из коэффициентов.
Решение:

1. Расчет парных и частных коэффициентов корреляции

Факторы, включаемые в модель должны иметь достаточно тесную связь с результативным признаком.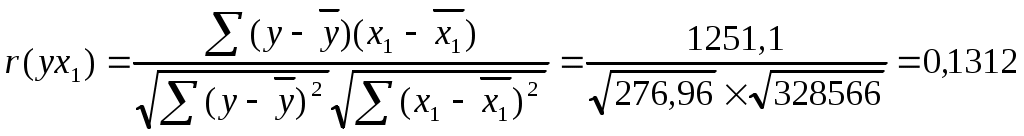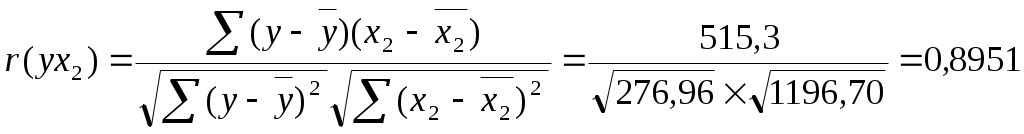





Вывод. Связь продолжительности жизни при рождении у с фактором х₁ очень слабая. Фактор х₁ не следует включать в модель.

Факторы, включаемые в модель должны быть слабо связаны между собой, факторы не должны быть коллинеарными (линейнозависимыми).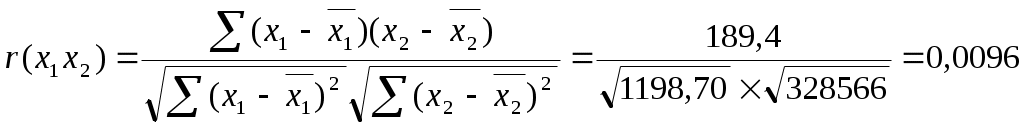



Вывод. Связь между факторами практически отсутствует, факторы не являются коллинеарными, линейнозависимыми.

Рассчитаем частные коэффициенты корреляции:



Т.е. если устранить влияние фактора х₂, то связь между у и х₁ будет слабой и прямой.



Т.е. если устранить влияние фактора х₁, то связь между у и х₂ будет очень тесной и прямой.



Т.е. если устранить влияние результативного признака у, то связь между х₁и х₂ будет слабой и обратной.

Целесообразно удалить из анализа фактор х₁ и строить регрессионную модель только с фактором х₂.
Таблица 5

Вспомогательная таблица для расчета коэффициентов парной корреляции

№	у	х1	х2							×	×	×
1	65,9	230	9,5	-8,9	-170	-10,5	79,21	28900	110,25	1513,0	93,45	1785,0
2	77,1	298	24,1	2,3	-102	4,1	5,29	10404	16,81	-234,6	9,43	-418,2
3	67,9	230	7,1	-6,9	-170	-12,9	47,61	28900	166,41	1173,0	89,01	2193,0
4	77,2	590	21,5	2,4	190	1,5	5,76	36100	2,25	456,0	3,60	285,0
5	77,4	295	24,5	2,6	-105	4,5	6,76	11025	20,25	-273,0	11,70	-472,5
6	78,7	350	29,5	3,9	-50	9,5	15,21	2500	90,25	-195,0	37,05	-475,0
7	77,2	340	22,4	2,4	-60	2,4	5,76	3600	5,76	-144,0	5,76	-144,0
8	78,2	370	25,1	3,4	-30	5,1	11,56	900	26,01	-102,0	17,34	-153,0
9	69,3	820	7,4	-5,5	420	-12,6	30,25	176400	158,76	-2310,0	69,30	-5292,0
10	70,3	326	3,5	-4,5	-74	-16,5	20,25	5476	272,25	333,0	74,25	1221,0
11	76,9	395	34,3	2,1	-5	14,3	4,41	25	204,49	-10,5	30,03	-71,5
12	81,5	556	31,1	6,7	156	11,1	44,89	24336	123,21	1045,2	74,37	1731,6
Итого	897,6	4800	240,0	0,0	0,0	0,0	276,96	328566	1196,70	1251,1	515,29	189,4
Среднее	74,80	400,00	20,00

2. Построим линейное уравнение множественной регрессии

Общий вид линейного двухфакторного уравнения регрессии:

, где

- расчетные (теоретические) значения результативного признака;

– оценки параметров линейного уравнения регрессии;

- коэффициенты регрессии, которые показывают насколько единиц в среднем изменяется значение результативного признака у при увеличении фактора на единицу измерения;

– значения факторных признаков.

Расчет средних квадратических отклонений:







Параметры модели найдем через линейные коэффициенты парной корреляции и средние квадратические отклонения:





74,80 – 0,0036×400 – 0,430×20 = 64,775

Получили двухфакторную модель регрессии:



Вывод. Коэффициент регрессии показывает, что при увеличении численности населения, обслуживаемого одним врачом на 1 чел значение продолжительности жизни в среднем увеличится на 0,0036 лет при неизменном значении фактора .

Коэффициент регрессии показывает, что при увеличении ВВП на душу населения на 1 тыс. долл. значение продолжительности жизни в среднем увеличится на 0,430 лет при неизменном значении фактора .

Коэффициент детерминации: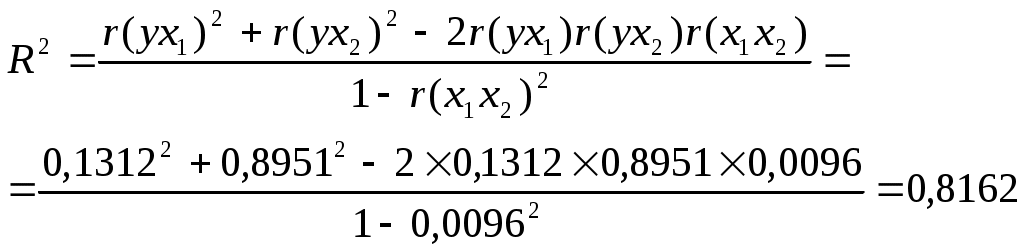



Вывод. 81,62% вариации результативного признака происходит под влиянием факторов , включенных в модель.

Скорректированный коэффициент детерминации позволяет учесть при оценке качества модели соотношение количества наблюдений и количества оцениваемых параметров модели.



Вывод. Показатели детерминации близки к единице, это говорит о высоком качестве модели регрессии.
3. Проверим значимость уравнения регрессии на 95% уровне

Выдвигаем нулевую гипотезу о том, что найденные показатели тесноты связи случайны, т.е. равны нулю:



Для проверки нулевой гипотезы рассчитываем значение F-критерия Фишера:



По таблице значений критерия Фишера находим табличное (критическое) значение критерия на уровне значимости α = 0,05 и с числом степеней свободы df₁ =k = 2 (число факторов в модели) и df₂ = n– k – 1 = 12 – 3 = 9:

F_табл = 4,26

Вывод. Поскольку F_табл < F, то нулевую гипотезу отклоняем. В качестве альтернативы принимаем гипотезу о том, что характеристики тесноты связи не случайны, т.е. значима построенная модель регрессии.
4. Рассчитаем коэффициенты эластичности

Коэффициент эластичности показывает насколько процентов в среднем изменяется значение результативного признака при увеличении фактора на 1% и рассчитывается по формуле:



Расчет коэффициентов эластичности:





Вывод. При увеличении фактора на 1% значение результативного признака у в среднем возрастает на 0019% при неизменном значении фактора . При увеличении фактора на 1% значение результативного признака у в среднем возрастает на 0,115% при неизменном значении фактора .
5) Построим 95% доверительные интервалы для коэффициентов регрессии

Находим стандартные ошибки коэффициентов регрессии: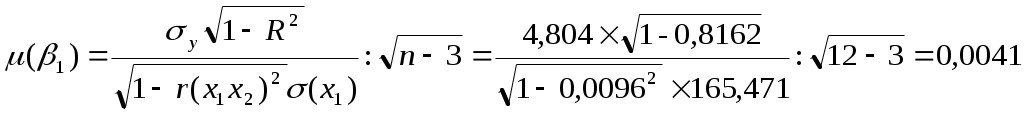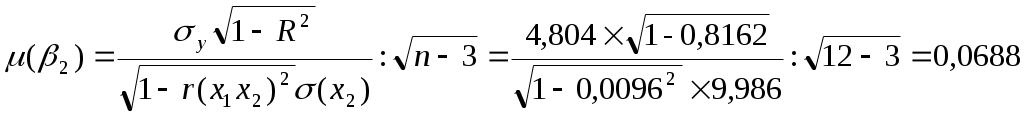





По таблице значений критерия Стьюдента находим табличное (критическое) значение критерия на уровне значимости α = 0,05 и с числом степеней свободы df = n– k – 1 = 12 – 3 = 9:

2,262

Интервальная оценка β₁:



-0,0058 0,0129

Вывод. С вероятностью 95% значение коэффициента регрессии β₁ будет находится в пределах от -0,0558 до 0,0129. Т.к. в доверительный интервал попадает 0, то параметр не является статистически значимым.

Доверительный интервал для коэффициента регрессии β₂:



0,2745 0,5856

Вывод. С вероятностью 95% значение коэффициента регрессии β₂ будет находится в пределах от 0,2745 до 0,5856. Т.е. с вероятностью 95% при увлечении ВВП на душу населения х₂ на 1 тыс. долл. значение продолжительности жизни у возрастет не менее, чем на 0,2745 лет, но не более чем на 0,5856 лет. Т.к. в доверительный интервал не попадает 0, то параметр является статистически значимым.