Трёхфазные цепи Трёхфазная система эдс
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
Трёхфазные цепиТрёхфазная система ЭДСТрёхфазная электрическая цепь может быть представлена как совокупность трех однофазных цепей, в которых действуют ЭДС одной и той же частоты, сдвинутых относительно друг друга на одну треть периода, т.е. на Принцип получения трёхфазной системы ЭДС показан на рис. 1. 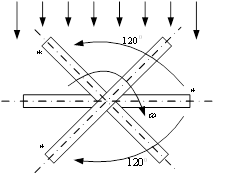 Рис. 1. Принцип получения трёхфазной системы ЭДС В равномерном магнитном поле с постоянной угловой скоростью ω вращаются три одинаковых, жестко скрепленных друг с другом, катушки. Плоскости катушек смещены в пространстве на 120° одна относительно другой. В каждой из катушек наводится синусоидальная ЭДС одинаковой амплитуды, но по фазе они сдвинуты на 120°. 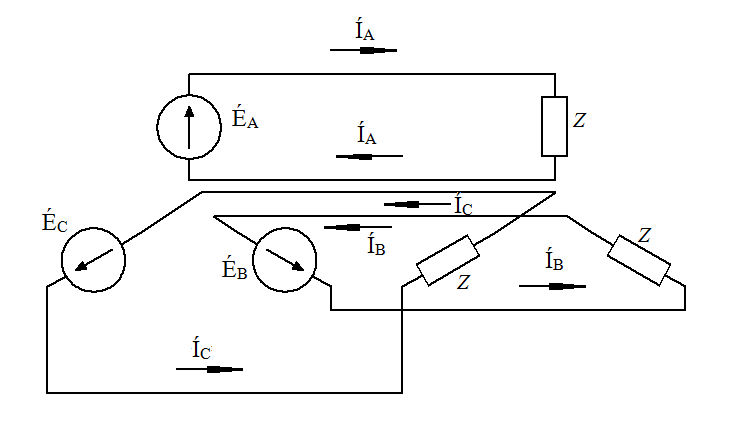 Рис. 2. Несвязная трёхфазная цепь. Если каждую катушку соединить с нагрузкой, то получим схему несвязанной трёхфазной цепи, показанную на рис. 2. Часть трёхфазной цепи, по которой протекает одинаковый ток, называют фазой. На рис. 2 фазы А, В, С изображены под углом 120°, для того что бы подчеркнуть, что ЭДС Е́А, Е́В, Е́С сдвинуты одна относительно другой на 120°. При равенстве амплитуд ЭДС и одинаковых сопротивлениях нагрузки токи ÍA, ÍB, ÍC так же равны по величине и сдвинуты друг относительно друга на одну треть периода, т. е. на 120°, образуя симметричную систему. График мгновенных значений ЭДС, наводимых в катушках схемы рис. 2, показан на рис. 3, векторная диаграмма ЭДС на рис. 4. 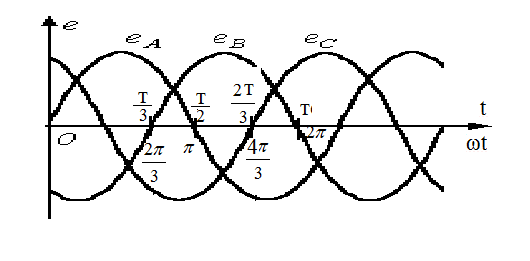 Рис. 3. График мгновенных значений ЭДС еА, еB, еC 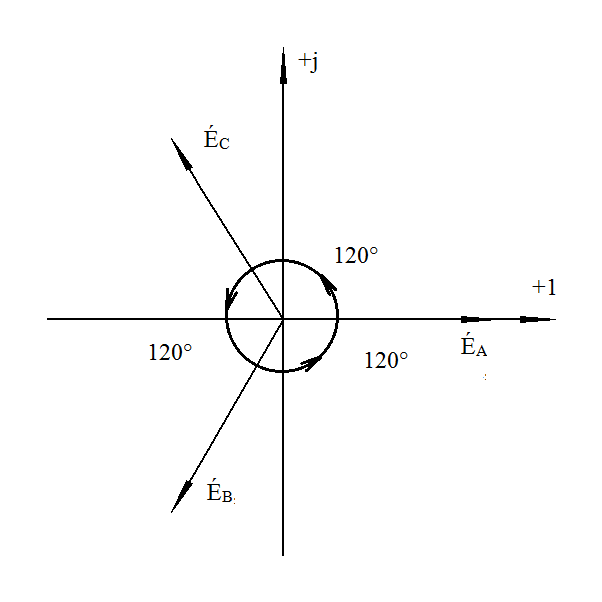 Рис. 4. Векторная диаграмма ЭДС М 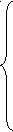 гновенные ЭДС, показанные на рис. 4, выражаются аналитически следующим образом: гновенные ЭДС, показанные на рис. 4, выражаются аналитически следующим образом:еА=Еmsinωt еB=Еmsin(ωt- еC=Еmsin(ωt+ Для осуществления трехфазной системы по схеме рис. 2 нужно шесть проводов, что очень неэкономно. Сумма токов ÍA+ÍB+ÍC при равенстве амплитуд ЭДС и одинаковых сопротивлениях нагрузки равна нулю в любой момент времени ÍA+ÍB+ÍC=0 (2) Поэтому если три провода, по которым токи возвращаются к источникам объединить в один провод, то ток в этом проводе будет равен нулю. Получится связанная трёхфазная цепь. Создание связанной трёхфазной цепи переменного тока явилось важным событием в истории электротехники. Связанная трёхфазная цепь показана на рис. 5. 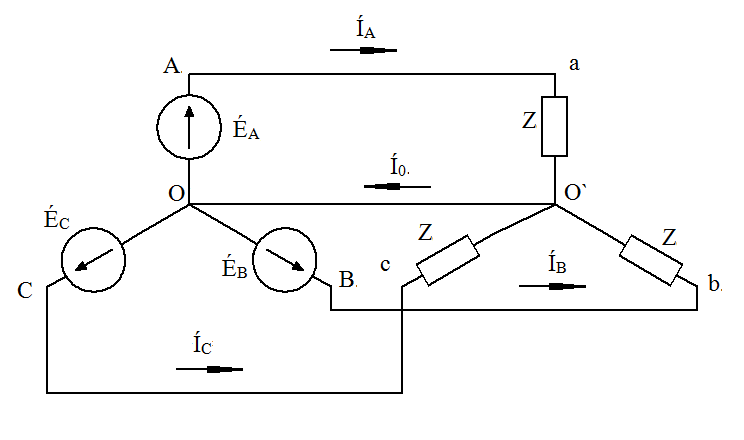 Рис. 5. Связанная трёхфазная цепь Данная схема по сравнению с схемой рис. 2 позволяет экономить два провода. Впервые связанную трёхфазную цепь переменного тока в 1889 г. осуществил выдающийся русский инженер и учёный Михаил Осипович Доливо-Добровольский (1862-1919 гг.). Им были разработаны основные звенья генерирования, передачи, распределения и преобразования электроэнергии трёхфазного тока; а именно: трёхфазный синхронный генератор, трёхфазный трансформатор, трёхфазный асинхронный двигатель. Изобретение М.О. Доливо-Добровольским трёхфазного асинхронного двигателя, являющегося самым дешёвым и простейшим двигателем переменного тока, существенно способствовало широкому промышленному внедрению трёхфазного тока. Аналогичным путём можно получить двух-, четырёх-, и вообще n-фазную систему ЭДС. Но наибольшее практическое применение получила трёхфазная система. Последовательность прохождения ЭДС через одинаковые значения (например через ноль) называют последовательностью фаз. Так на рис. 3 через ноль проходит сначала еА, затем еВ, и лишь потом еС. Последовательность фаз будет – А, В, С. Принцип работы трёхфазного синхронного генератора.В отличие от рис. 1 в трёхфазном синхронном генераторе обмотки А, В, С являются неподвижными и размещены они в пазах статора. Каждая обмотка размещается в одной трети пазов статора. Автоматически получается сдвиг на 120° плоскостей обмоток относительно друг друга. М. О. Доливо-Добровольский поменял местами обмотки и поле. Раньше магнитное поле было неподвижным, а вращались обмотки в поле (рис. 1). Теперь обмотки стали неподвижными, а вращается магнитное поле, создаваемое обмоткой ротора, по которым протекает постоянный ток. Питание обмотки ротора происходит через кольца со скользящими контактами. Ротор вращается равномерно с угловой скоростью ω от внешнего двигателя, например, бензинового двигателя, гидротурбины, газовой турбины и т. д. (рис. 6). 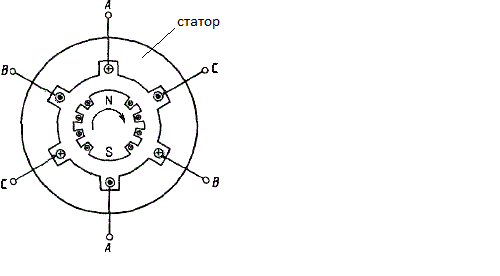 Рис. 6. Трёхфазный синхронный генератор Угловая скорость вращения ротора равны угловой скорости вращающегося магнитного поля. Поэтому говорят, что магнитное поле вращается синхронно с ротором. Отсюда название трёхфазный синхронный генератор. Вращающееся магнитное поле пересекает обмотки неподвижного статора и в них наводится синусоидальная ЭДС. Благодаря тому, что фазы А, В, С неподвижны, присоединение трёхфазного генератора к внешней цепи происходит очень просто и надежно с помощью болтовых соединений. Магнитная цепь в такой конструкции почти замкнута, имеется только небольшой зазор между статором и ротором, что позволяет получить значительный магнитный поток при относительно небольшой МДС обмотки ротора. У мощных синхронных генераторов в качестве магнитного поля используется электромагнитное поле постоянного тока. Подвод питания к вращающейся обмотке ротора происходит через скользящие контакты. И это пожалуй самое слабое место. У маломощных синхронных генераторов отсутствует и это слабое место, так как ротор у них представляет двухполюсный или многополюсный постоянный магнит. И нет никаких скользящих контактов. Трёхфазная цепь. Расширение понятия фазы.Совокупность трёхфазной системы ЭДС, трёхфазных нагрузок и соединительных проводов называют трёхфазной цепью. Под фазой трёхфазной цепи, как уже было сказано, понимают участок трёхфазной цепи, по которому протекает одинаковый ток. В литературе фазой иногда называют однофазную цепь, входящую в состав многофазной цепи. Под фазой понимают так же аргумент синусоидально изменяющейся величины, что ранее рассматривалось. Таким образом, в зависимости от рассматриваемого вопроса ваза это либо участок трёхфазной цепи, либо аргумент синусоидально изменяющейся величины. Соединение обмоток генератора и нагрузок звездой и треугольником.На электрической схеме обмотки генератора обозначают буквами А, В, С; буквы расставляют: А – у начала первой фазы, В – у начала второй фазы, С – у начала третьей фазы. При соединении обмоток генератора звездой одноимённые зажимы (например, концы x, y, z) трёх обмоток объединяют в одну точку О (рис. 7) 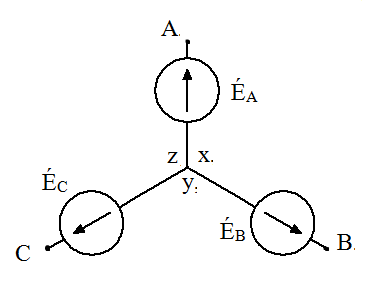 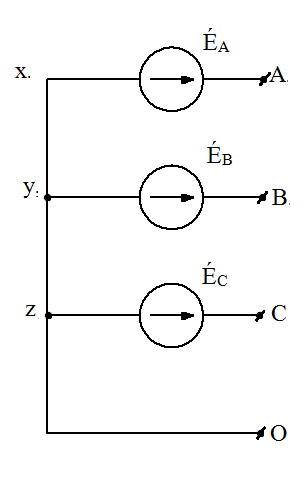 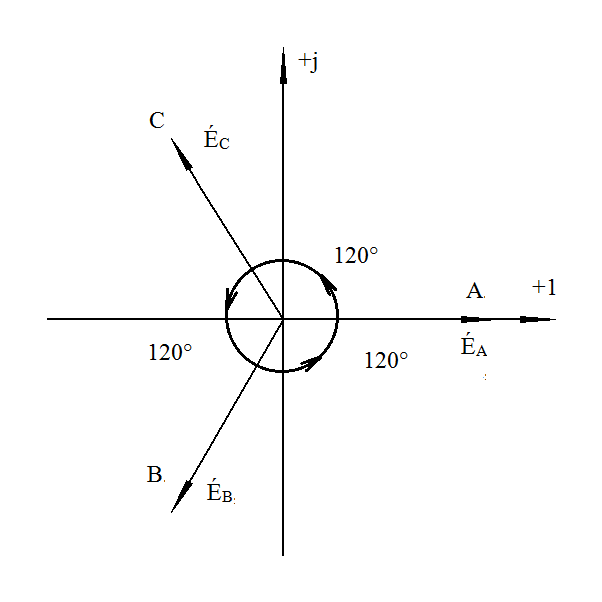 а) б) в) Рис. 7. Соединение обмоток генератора звездой и векторная диаграмма ЭДС Е́А, Е́В, Е́С На рис. 7, а и 7, б показаны различные схемы изображения фаз генератора. На рис. 7, в показана векторная диаграмма фазных ЭДС генератора. Векторы Е́А, Е́В, Е́С сдвинуты на 120° один относительно другого и получается симметричная система векторов. Сумма векторов любой симметричной системы равна нулю. Точку О называют нулевой точкой генератора. При соединении обмоток генератора треугольником (рис. 8) начало одной фазной обмотки с концом следующей по порядку фазной обмотки так, что все три обмотки образуют замкнутый треугольник, причем направление ЭДС в контуре треугольника совпадают и сумма ЭДС равна нулю. Поэтому если к зажимам А, В, С не присоединена нагрузка, то по обмоткам генератора не будет протекать ток. 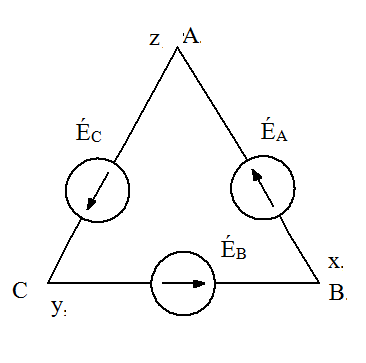 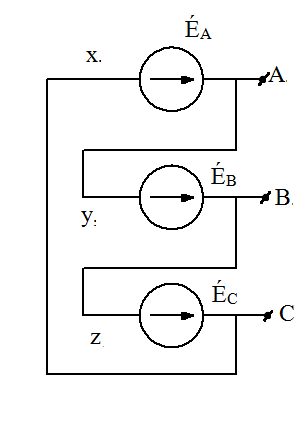 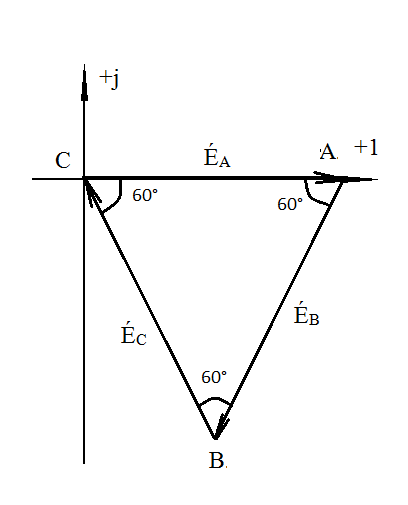 а) б) в) Рис. 8. Соединение обмоток треугольником и векторная диаграмма ЭДС Е́А, Е́В, Е́С На рис. 8, а и 8, б показаны различные схемы изображения фаз генератора. На рис. 8, в представлена векторная диаграмма фазных ЭДС генератора Е́А, Е́В, Е́С. Ради упрощения на рис. 7 и 8 показаны только ЭДС генератора; обмотки и их сопротивления на схеме не показаны. Нагрузки в трёхфазной цепи так же могут быть соединены звездой или треугольником (рис. 9). Точка О` называется нулевой точкой нагрузки. 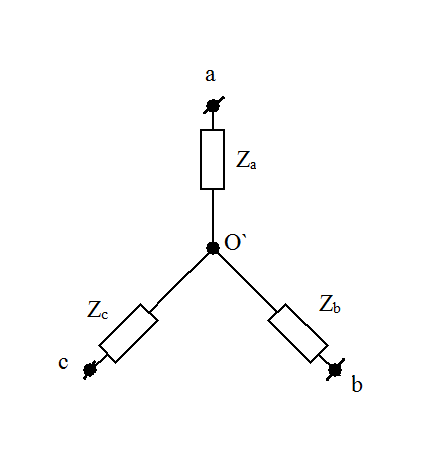 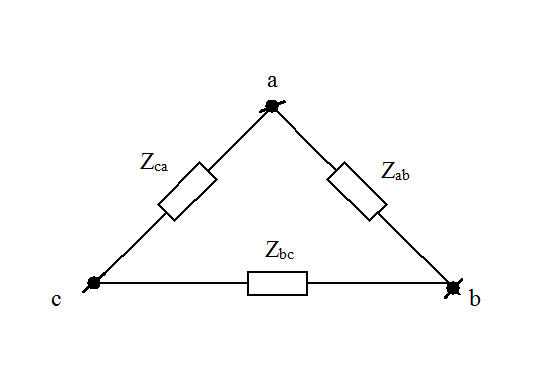 Рис. 9 Соединение нагрузок звездой и треугольником Основные схемы соединения трёхфазных цепей. Соотношения между линейными и фазными величинами.Существует пять способов соединения трёхфазного генератора и трёхфазной нагрузки. Рассмотрим их все поочерёдно. Звезда – звезда с нулевым проводом (рис. 10)В этой схеме и обмотки генератора и нагрузки соединены звездой и имеется нулевой провод.  Рис. 10. Схема соединений звезда – звезда с нулевым проводом Рассмотрим все обозначения, принятые в трёхфазных цепях. Нулевой провод – провод, соединяющий нулевую точку генератора О и нулевую точку нагрузки О`. Ток текущий по нулевому проводу называют нулевым током и обозначают Í0. Линейный провод – провода, соединяющие точки А, В, С генератора и соответствующие точки а, b, с нагрузок. Токи, текущие по линейным проводам, называют линейными токами и обозначают ÍA, ÍB, ÍC. Положительное направление линейных токов всегда от генератора к нагрузке. Направление нулевого тока Í0 всегда от нагрузки к генератору. Модуль линейного тока обозначается IЛ, модуль тока нулевого провода I0. Зажимы А, В, С генератора не схеме всегда обозначается большими буквами, зажимы а, b, с нагрузок – маленькими. Между точками А и О, В и О, С и О – фазные ЭДС генератора Е́А, Е́В, Е́С соответственно. Между зажимами А, В, С – линейные ЭДС генератора Е́АВ, Е́ВС, Е́СА. Напряжение между точками а и о`, b и о`, с и о` называют фазными напряжениями нагрузки и обозначают ÚA, ÚB, ÚC. Модуль фазного напряжения обозначается Uф. Напряжения между точками а, b, с нагрузки, т. е. между линейными проводами в месте присоединения нагрузки, называется линейным напряжением нагрузки и обозначаются ÚAВ, ÚBС, ÚCА. Модуль линейного напряжения – UЛ. Каждую из трёх обмоток генератора называют фазой генератора, каждую из трёх нагрузок – фазой нагрузки. Токи, протекающие по фазам генератора, называют фазовыми токами генератора. Токи, протекающие по фазам нагрузки, называют фазовыми токами нагрузки. Модуль фазового тока обозначается Iф. Нагрузка называется равномерной или симметричной, когда во всех фазах включена одинаковая нагрузка по величине и по характеру. Для генератора и равномерной нагрузки справедлива векторная диаграмма рис. 11. 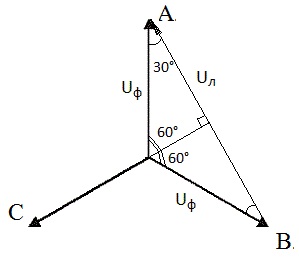 Рис. 11. Векторная диаграмма Для данной схемы соединения звезда – звезда с нулевым проводом в фазах генератора и нагрузки течёт тот же ток, что и в линейном проводе. Отдельно запишем соотношение между линейными и фазными величинами для генератора и нагрузки. Для генератора: Для нагрузки: Звезда – звезда без нулевого провода (рис. 12)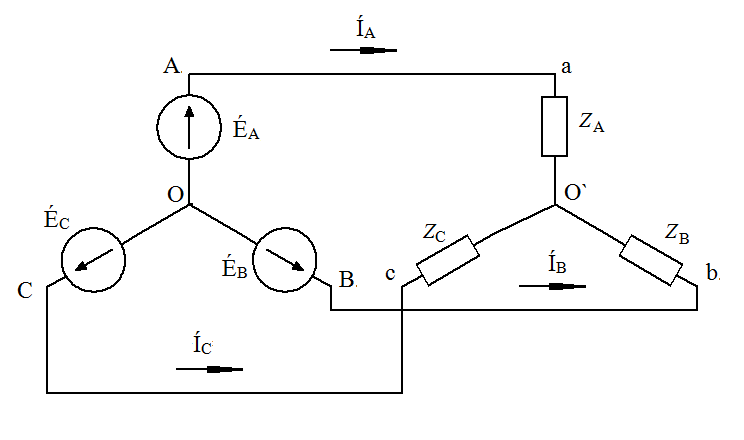 Рис. 12. Схема соединений звезда – звезда без нулевого провода Для генератора: Для нагрузки: Звезда – треугольник (рис. 13)В данной схеме обмотки генератора включены звездой, а нагрузки треугольником. В этой схеме кроме линейных токов нагрузок ÍA, ÍB, ÍC появляются фазные токи нагрузок Íab, Íbc, Íca, протекающие по треугольнику нагрузок. 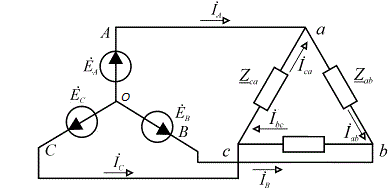 Рис. 13. Схема соединения звезда - треугольник При равномерной нагрузке фазные токи нагрузок Íab, Íbc, Íca образуют равносторонний треугольник (рис. 14): 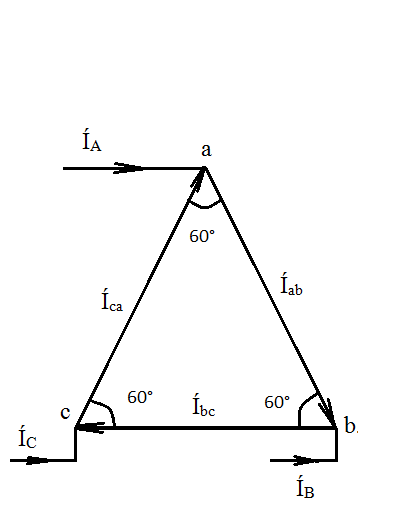 Рис. 14. Фазные токи нагрузок Для узлов а, b, с по первому закону Кирхгофа можно записать: ÍA = Íab - Íca; (12) ÍB = Íbc - Íab; (13) ÍC = Íca - Íbc; (14) Изобразим векторную диаграмму согласно выражению (12), т. е. сложим вектор Íab с вектором - Íca, что показано на рис. 15. Сумма этих векторов равна линейному току ÍA. 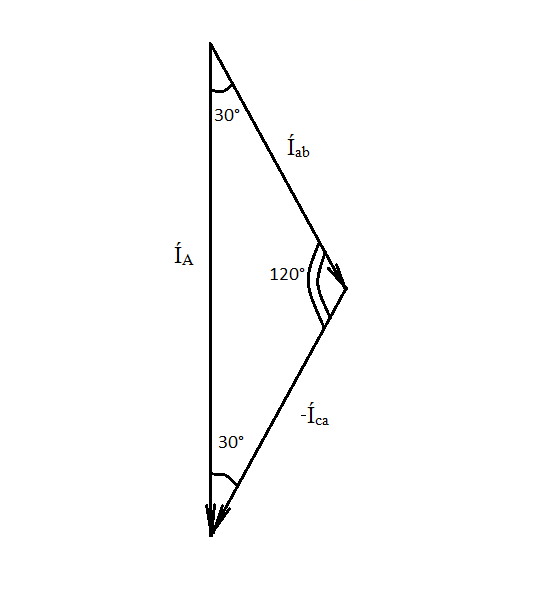 Рис. 15. Векторная диаграмма Между фазными токами нагрузок Íab, Íbc, Íca при равномерной нагрузке углы 120°. На векторной диаграмме фазные токи Íab, Íbc и линейный ток ÍA образуют равнобедренный треугольник, в котором углы между фазными токами нагрузок и линейным током равны 30°. Это справедливо и для выражений (13) и (14). Тогда можно обобщить (рис. 16): 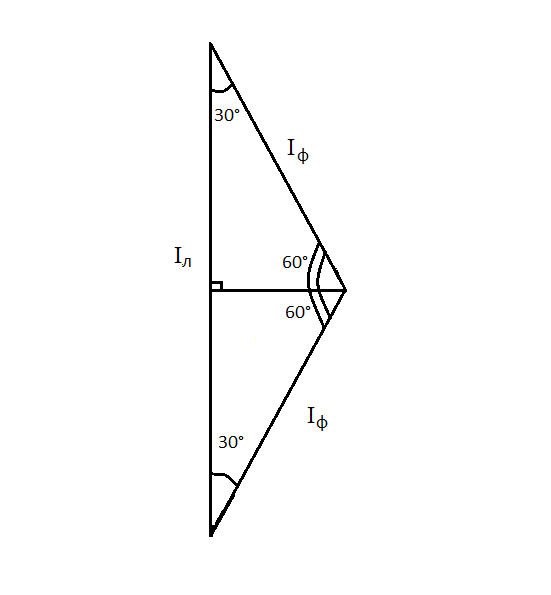 Рис. 16. Соотношение между линейным и фазным токами Для рис. 16 можно записать: Таким образом для схемы звезда – треугольник при равномерной нагрузке соответствия между линейными и фазными величинами выглядят следующим образом: Для генератора: Для нагрузки: Треугольник – треугольник (рис. 17) Рис. 17. Схема соединений треугольник - треугольник При равномерной нагрузке соотношения между линейными и фазными величинами выглядят следующим образом: Для генератора: Для нагрузки: Треугольник – звезда (рис. 18)При равномерной нагрузке соотношения между линейными и фазными величинами выглядит: 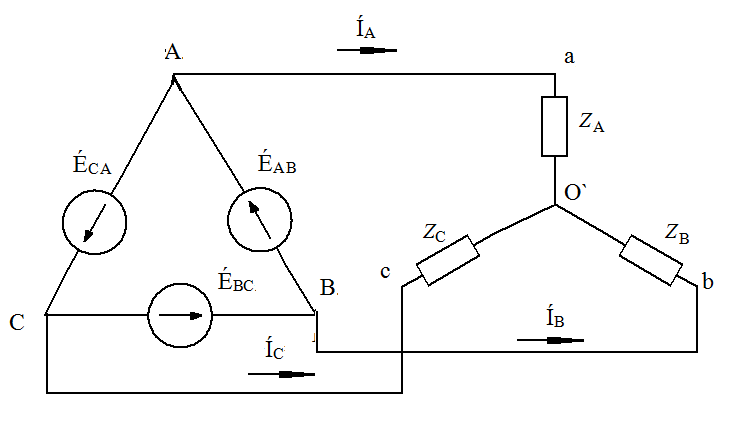 Рис. 18. Схема соединения треугольник - звезда Для генератора: Для нагрузки: Выше рассмотренные соотношения между линейными и фазными величинами всегда соблюдаются для генератора при любой нагрузке равномерной или неравномерной. Рассмотренные соотношения между линейными и фазными величинами для нагрузки соблюдаются только в случае равномерной нагрузки. Преимущества трёхфазных системШирокое распространение трёхфазных систем объясняется главным образом тремя основными причинами:
Расчёт трёхфазных цепейТрёхфазные цепи являются разновидностью цепей синусоидального тока и потому расчёт и исследование процессов в них производится теми же методами и приёмами, которые рассматривались ранее. Для цепей трёхфазного тока применим так же символический метод расчёта, могут строиться векторные, топографические и круговые диаграммы. Аналитический расчёт рекомендуется сопровождать построением векторных или топографических диаграмм, что помогает находить ошибки при аналитическом расчёте, если последние возникают. Оператор а трёхфазной системыУсловимся комплексное число еj120° по модулю равное единице, обозначить через а и называть оператором трёхфазной системы еj120° = а (28) Тогда еj240° =(еj120° )2 = а2 (29) Умножение любого вектора на а означает поворот его без изменения модуля на 120° против часовой стрелки. Умножение вектора на а2 поворачивает его на угол 240° против часовой стрелки, или, что то же самое, поворачивает его на 120° по часовой стрелке. Три вектора 1, а, а2 – образуют симметричную трёхфазную систему, а сумма векторов любой симметричной системы равна нулю (рис. 19). 1 + а + а2 = 0 (30) 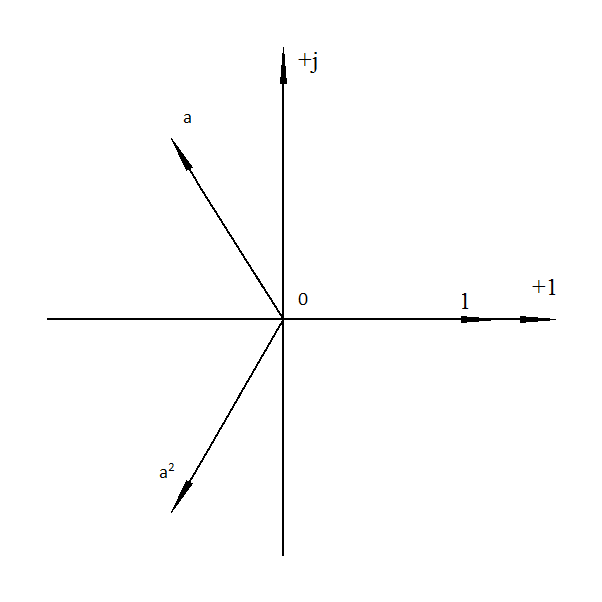 Рис. 19. Симметричная система трёх единичных векторов С помощью оператора а можно выразить ЭДС Е́В и Е́С симметричной трёхфазной системы через ЭДС Е́А: Е́В = а2* Е́А; Е́С = а*Е́А; (30) Расчёт схемы звезда – звезда с нулевым проводом (рис. 20)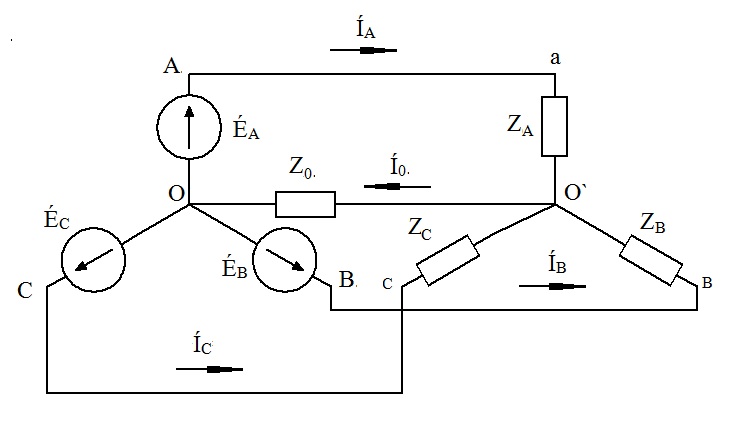 Рис. 20. Схема соединения звезда – звезда с нулевым проводом Если нулевой провод обладает весьма малым сопротивлением, т.е. Z0=0, то потенциал точки О` практически равен потенциалу точки О, точки О` и О фактически представляют собой одну точку: ϕ́0 = ϕ́0` (32) При этом в схеме образуются три обособленных контура, токи в которых даже при неравномерной нагрузке можно определить по простым формулам: 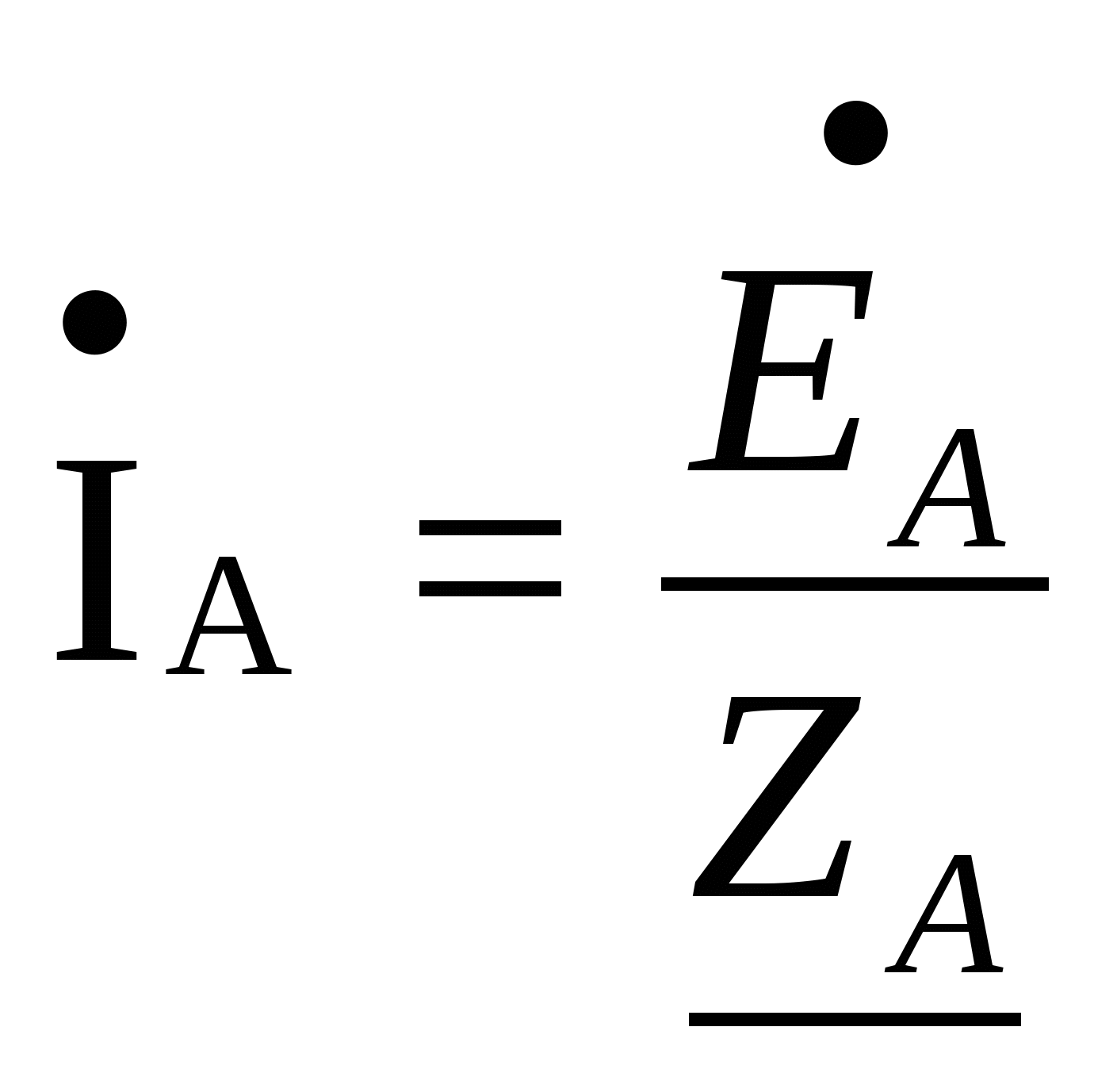 ; ; 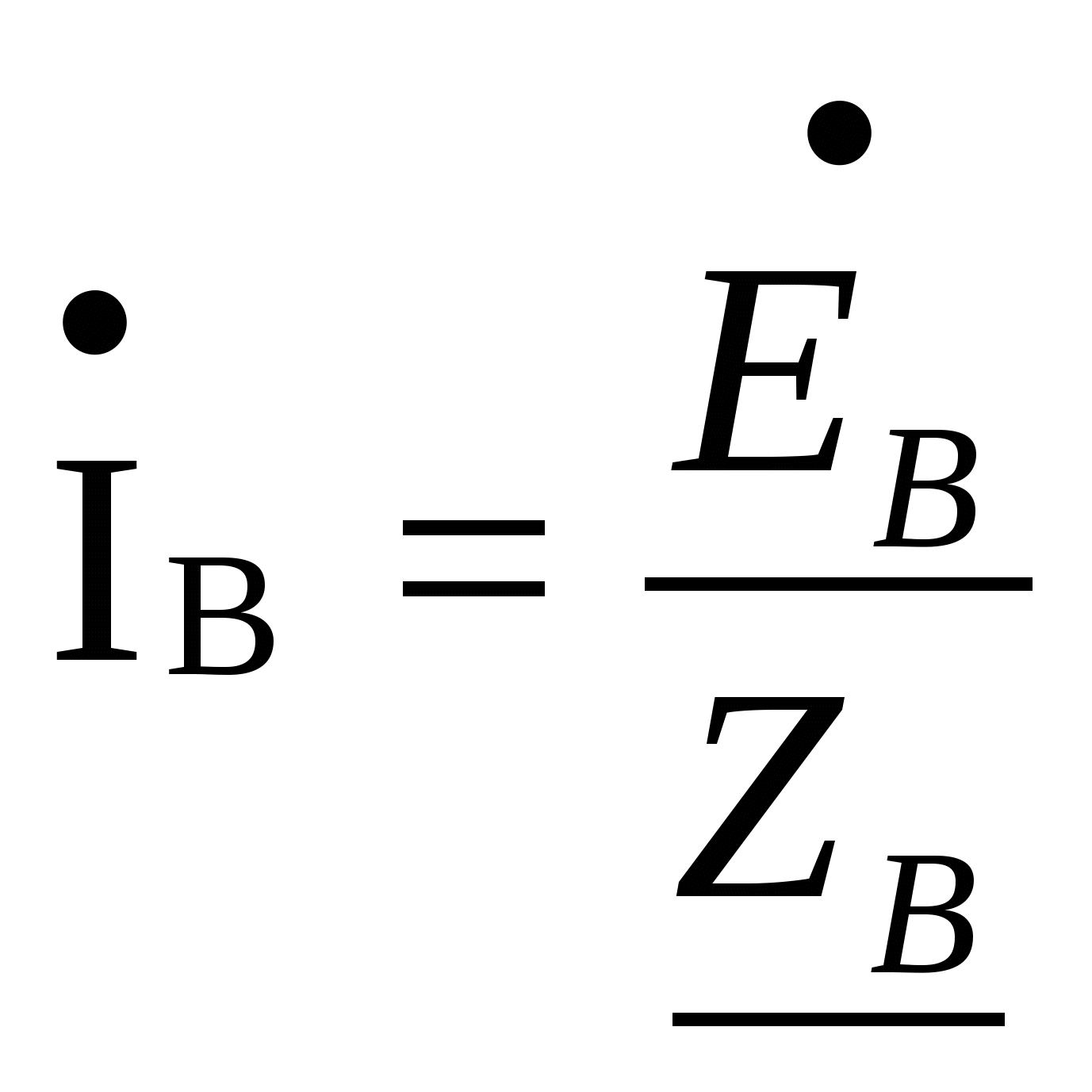 ; ; 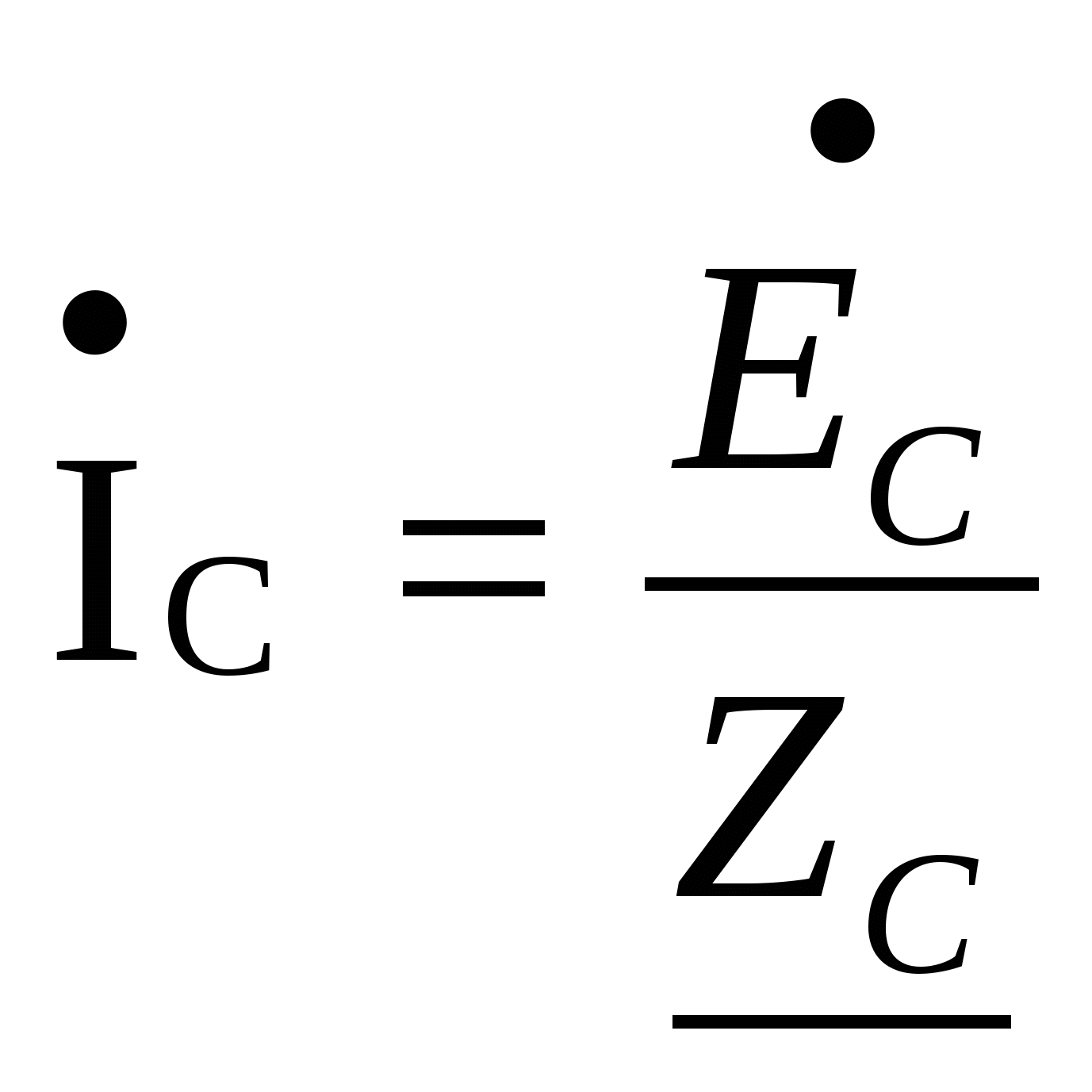 ; (33) ; (33)При равномерно нагрузке линейные токи ÍA, ÍB, ÍC образуют симметричную систему векторов, т. е. сдвинутых на 120° один относительно другого. Их сумма равна нулю: ÍA + ÍB + ÍC = 0, (34) т. е. ток нулевого провода равен нулю. При неравномерной нагрузке линейные тока могут оказаться под любым углом по отношению друг к другу. Появляется ток нулевого провода Í0, который можно определить по первому закону Кирхгофа для любого узла: Í0 = ÍA + ÍB + ÍC (35) Если в нулевом проводе есть сопротивление Z0, то расчёт следует проводить по методу узловых потенциалов. Точка О генератора всегда заземляется по правилам техники безопасности, т. е. ϕ́0 = 0 (36) Составим уравнение для узла О`: ϕ́0`(YA+YB+YC+Y0) = Е́АYA+ Е́ВYВ+ Е́СYС, отсюда получаем 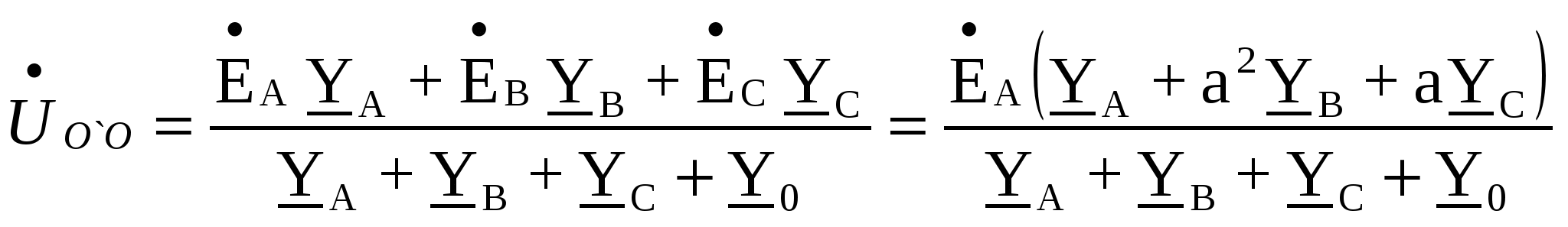 (37) (37)где YA, YB, YC, Y0 – комплексные проводимости фаз А, В, С и нулевого провода соответственно. Если нагрузка неравномерная ÚAO`=ÉА - ÚO`О, ÚВO`=ÉВ - ÚO`О, ÚСO`=ÉС - ÚO`О (38) А токи в фазах нагрузки будут найдены: 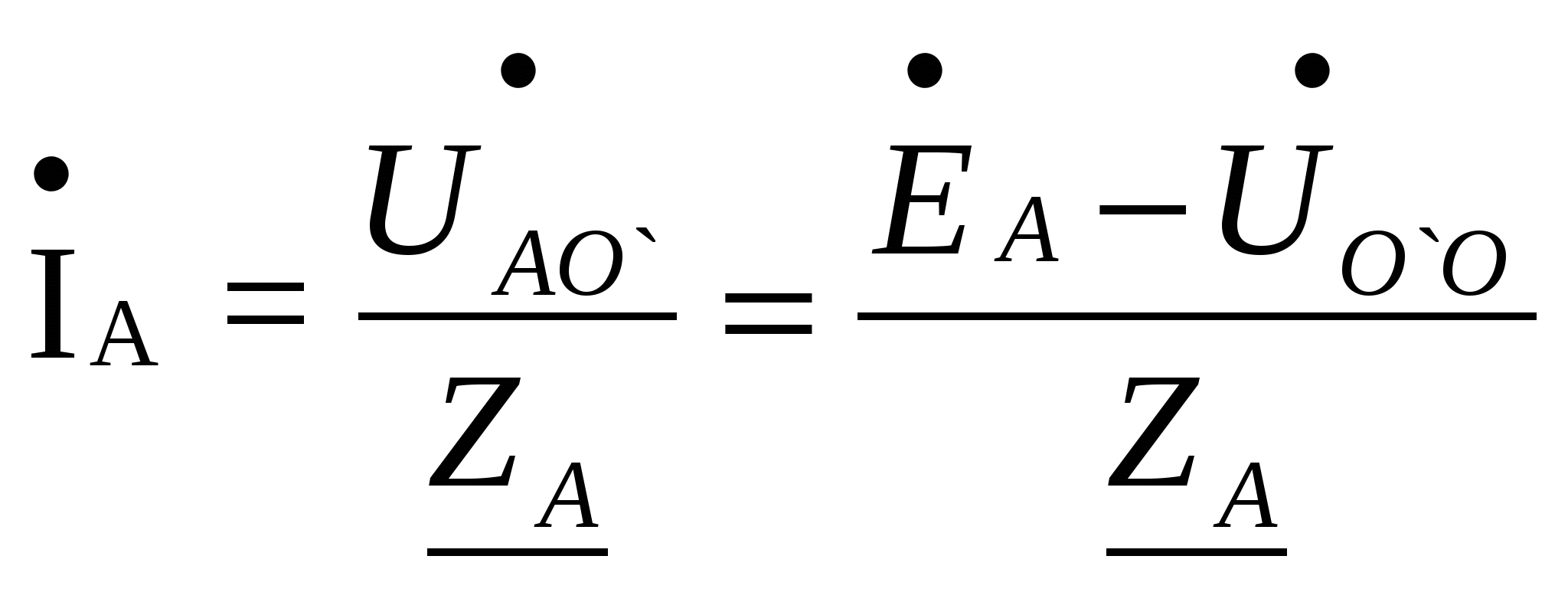 ; (39) ; (39)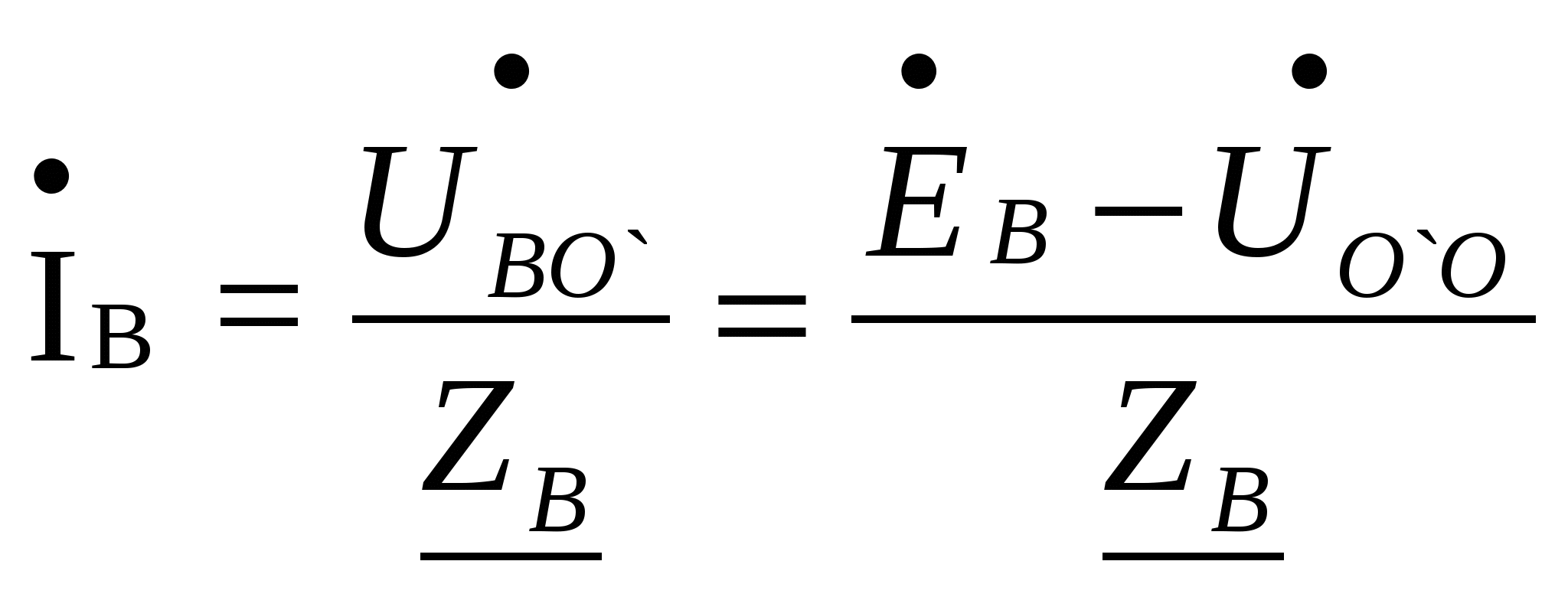 ; (40) ; (40)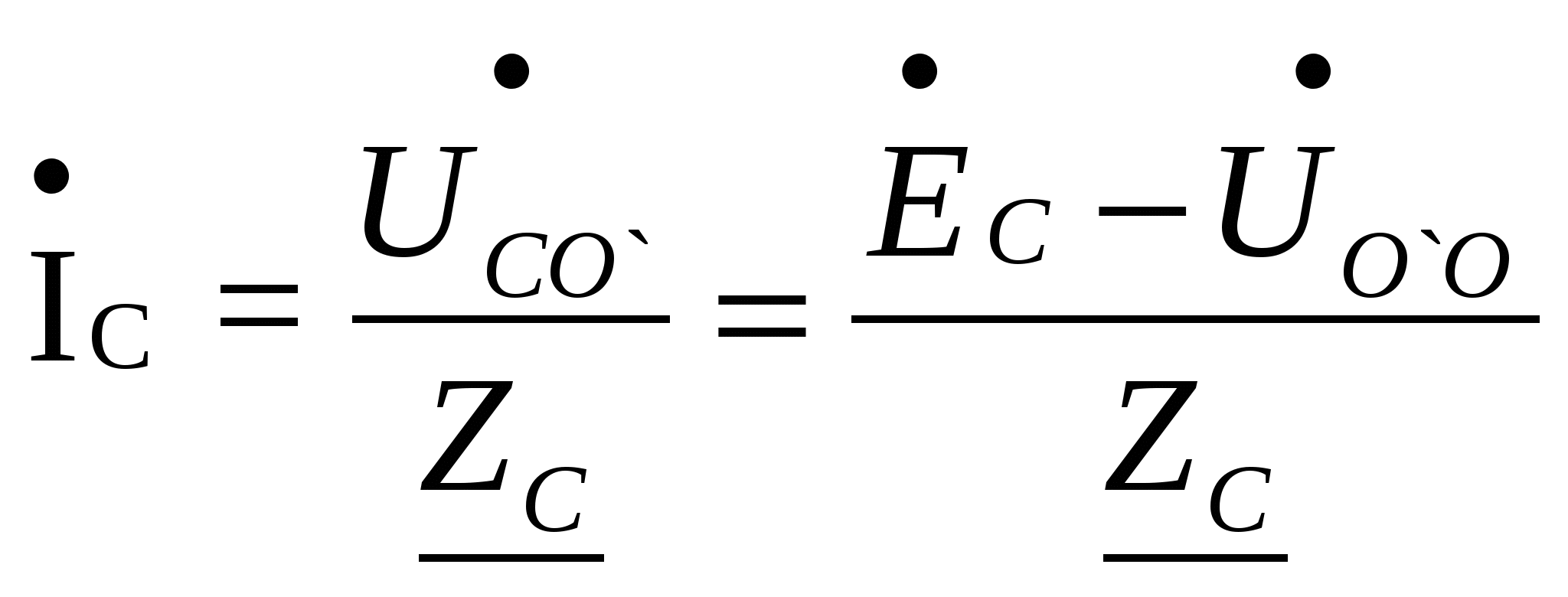 ; (41) ; (41)Линейные токи ÍA, ÍB, ÍC образуют несимметричную систему и появляется ток нулевого провода Í0, который можно найти по первому закону Кирхгофа: Í0 = ÍA + ÍB + ÍC, (42) или по формуле 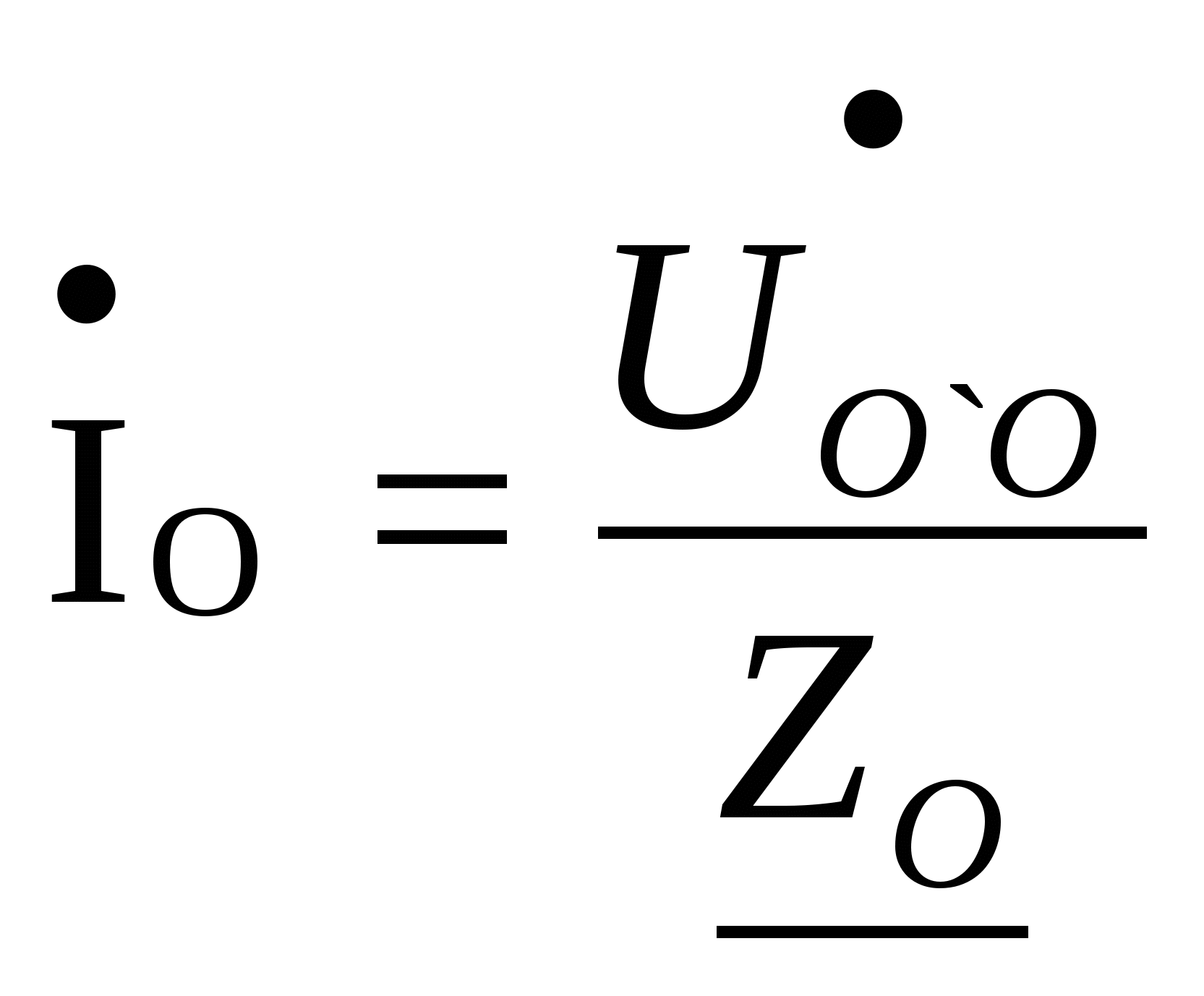 (43) (43)Естественно, по обеим формулам должно получиться одно и то же. Если нагрузка равномерная 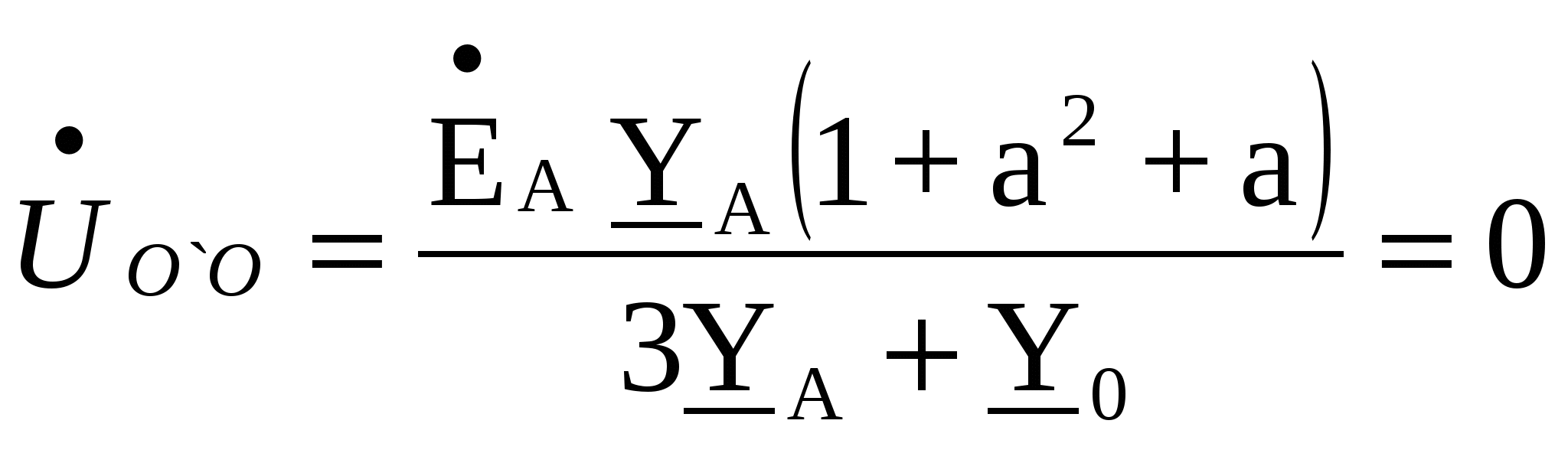 (44) (44)так как 1 + а2 + а = 0 Линейные токи ÍA, ÍB, ÍC образуют симметричную систему: 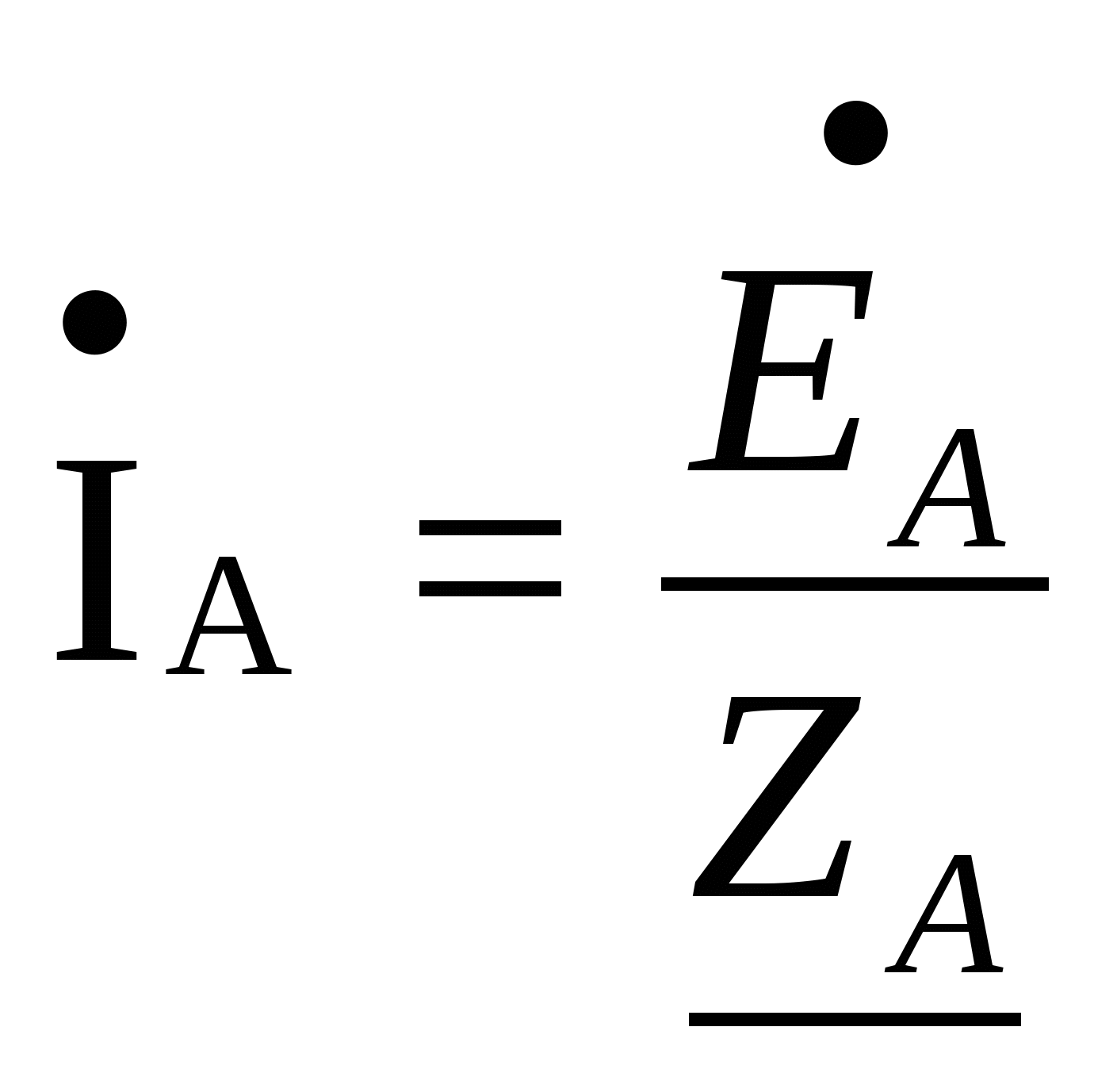 ; ; Ток нулевого провода будет равен нулю: Í0 = ÍA + ÍB + ÍC = 0. (46) Расчёт схемы звезда – звезда без нулевого проводаРасчёт такой же, как и для схемы звезда - звезда с нулевым проводом. Только будет отсутствовать комплексная проводимость нулевого провода Y0, так как нет нулевого провода (рис. 21). 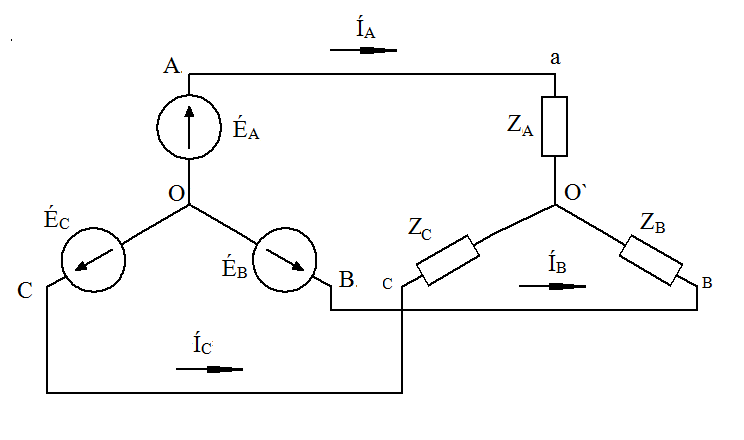 Рис. 21. Схема соединений звезда – звезда без нулевого провода Для этой схемы 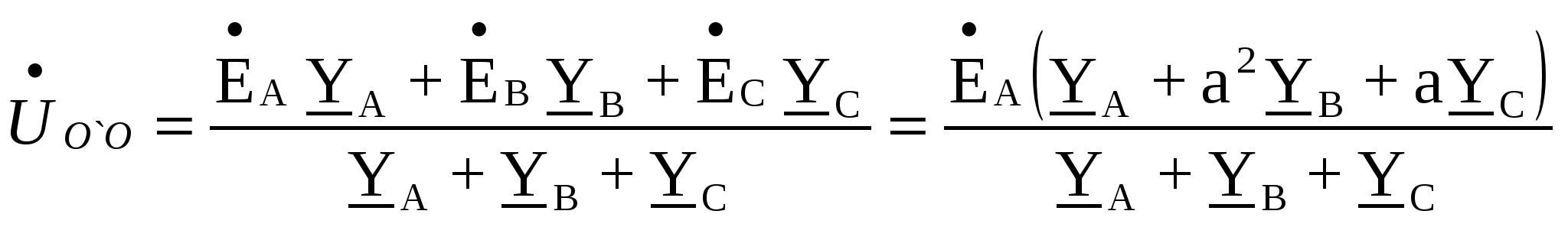 (47) (47)Если нагрузка неравномерная ÚAO`=ÉА - ÚO`О, ÚВO`=ÉВ - ÚO`О, ÚСO`=ÉС - ÚO`О (48) А токи в фазах нагрузки будут найдены: 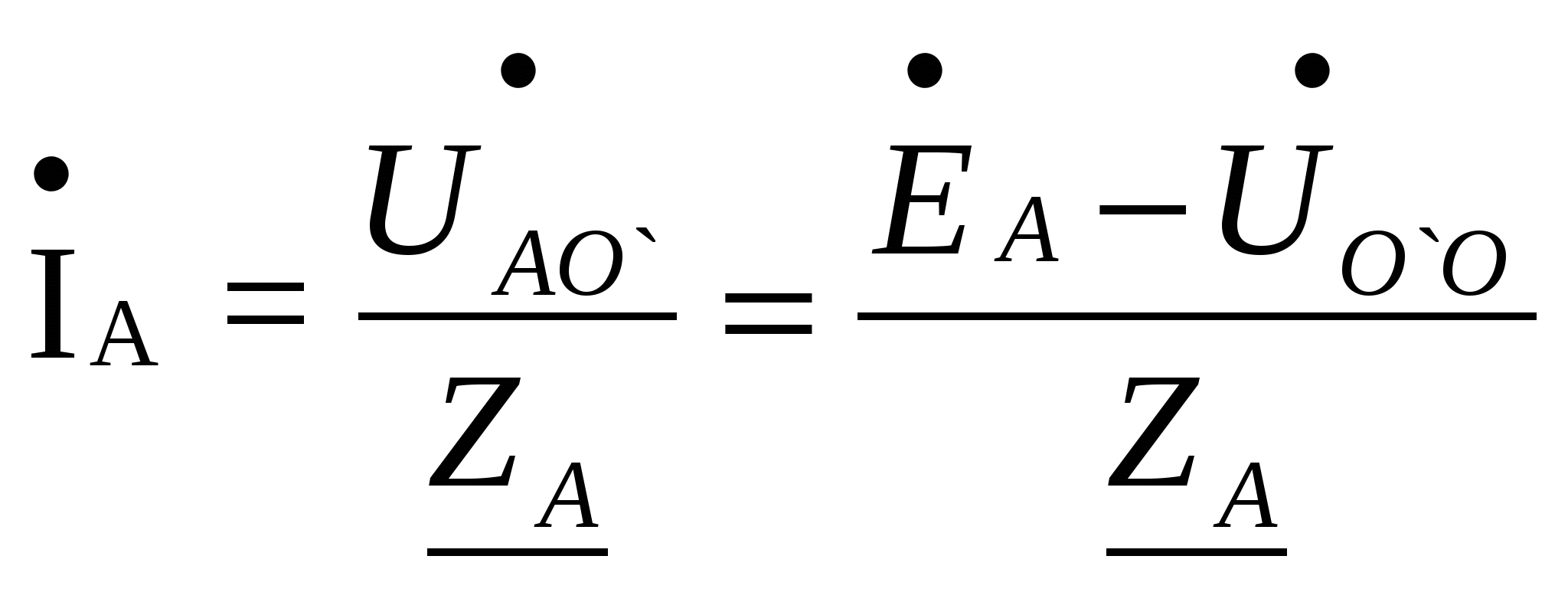 ; (49) ; (49)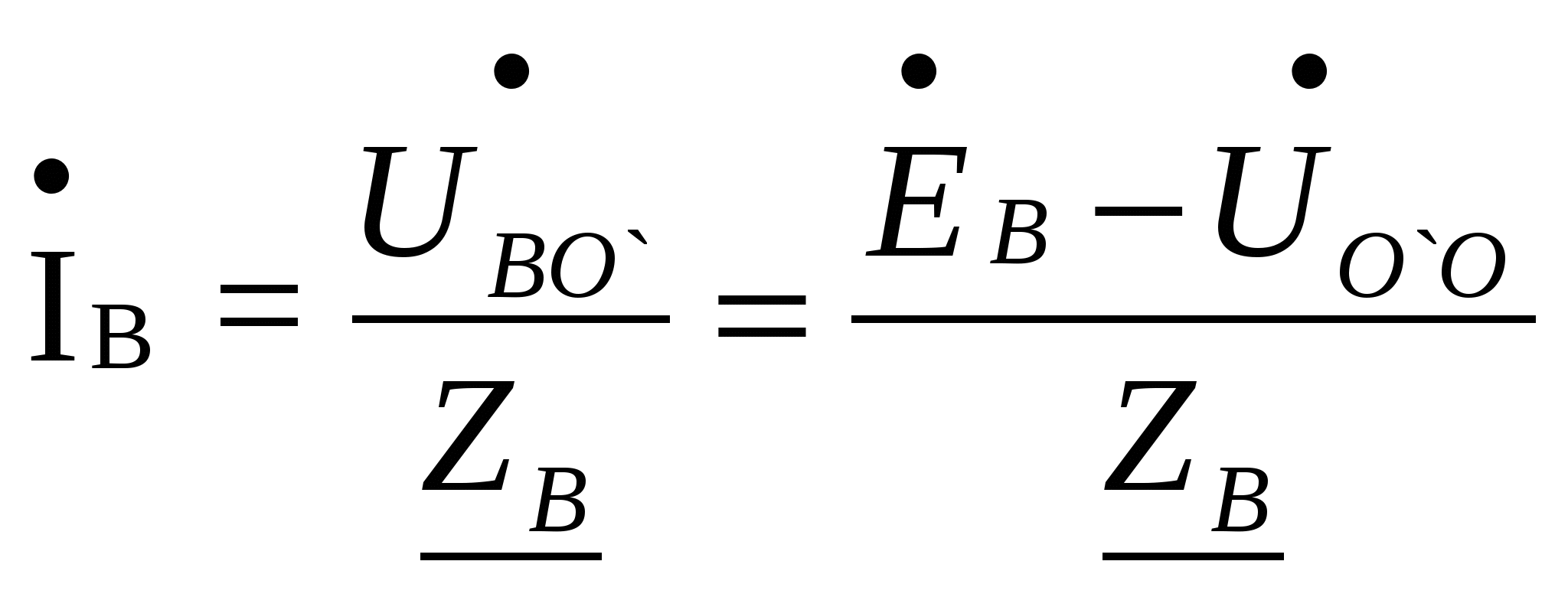 ; (50) ; (50)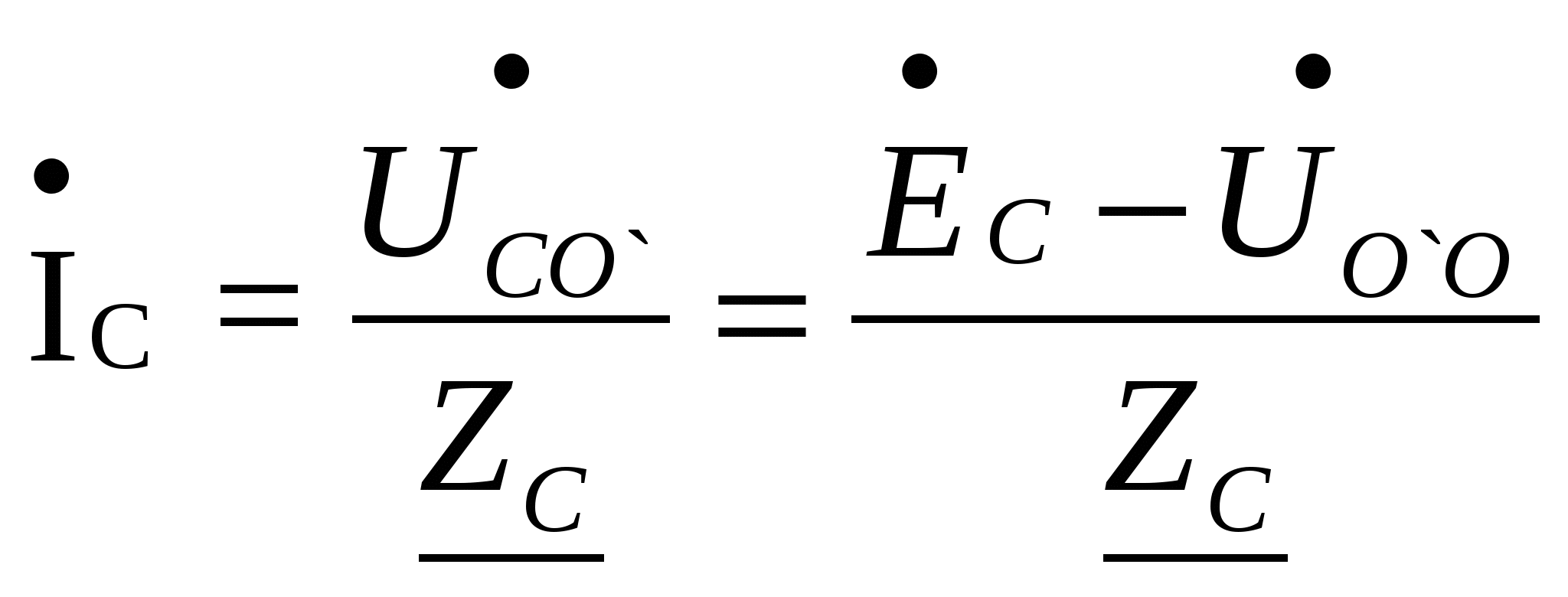 ; (51) ; (51)Линейные токи по отношению друг к другу могут находиться под любым углом, т. е. образуют несимметричную систему векторов. По первому закону Кирхгофа их сумма должна равняться нулю: ÍA + ÍB + ÍC = 0. (52) Если нагрузка равномерная 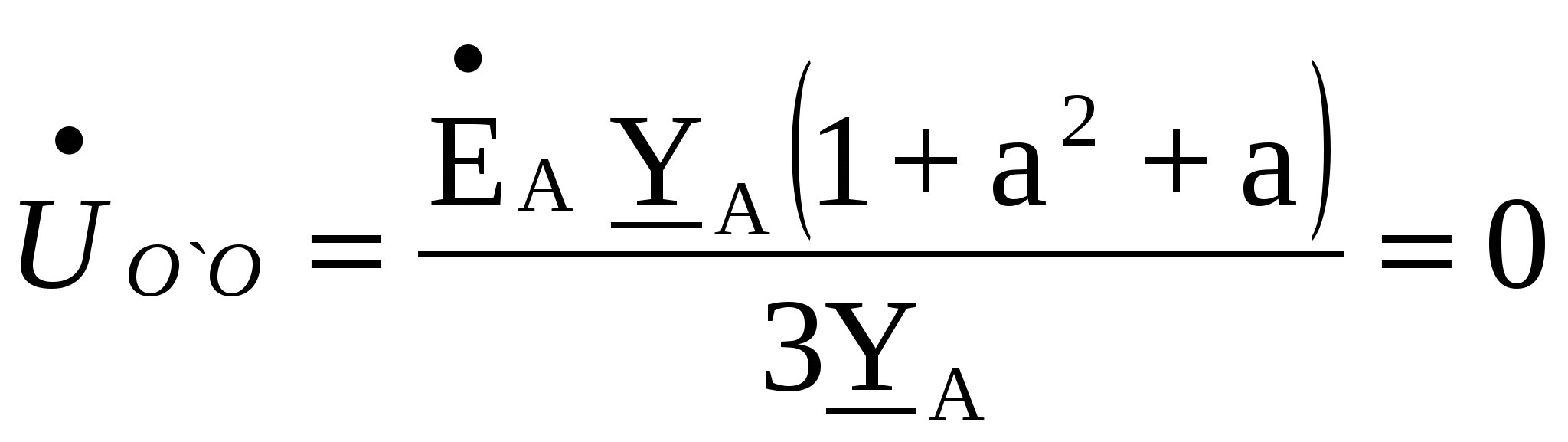 (53) (53)так как 1 + а2 + а = 0 В этом случае линейные токи ÍA, ÍB, ÍC образуют симметричную систему векторов: 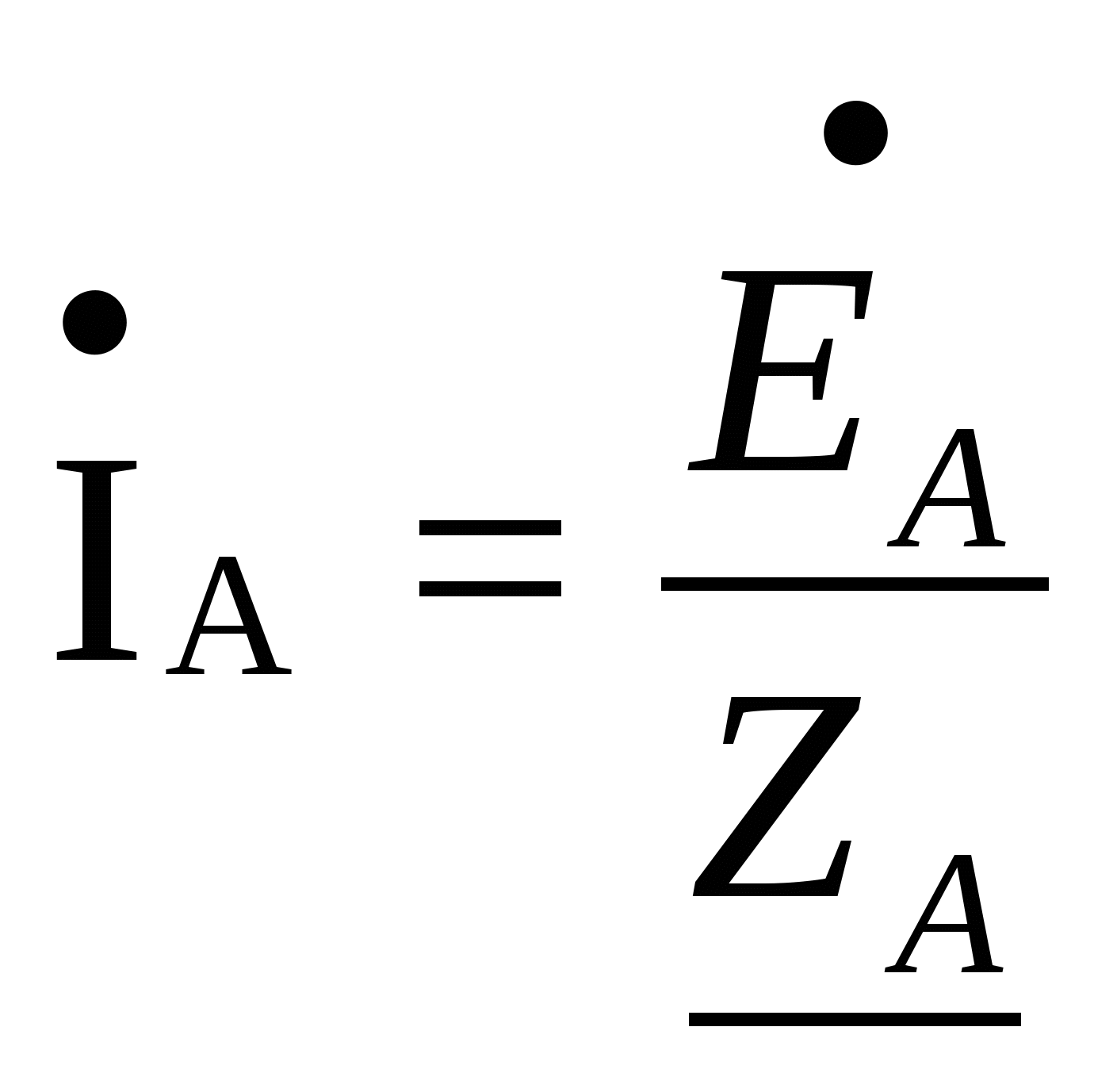 ; ; Естественно, что: Í0 = ÍA + ÍB + ÍC = 0. (55) Расчёт схемы, когда нагрузка соединена звездой и известны линейные напряжения (рис. 22)Сюда подходят схемы соединений треугольник – звезда и звезда – звезда без нулевого провода. 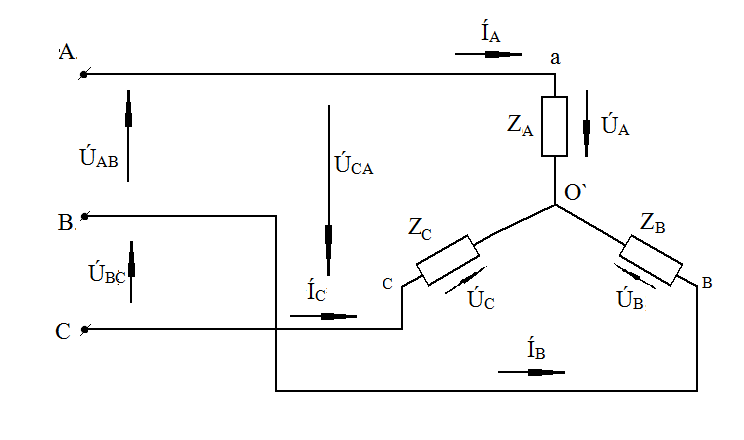 Рис. 22. Электрическая схема По первому закону Кирхгофа можно записать: ÍA + ÍB + ÍC = 0 (56) Токи в фазах нагрузки можно записать через фазные напряжения нагрузок ÚA, ÚB, ÚC и комплексные проводимости нагрузок: ÍA = ÚAYA; ÍВ = ÚВYВ; ÍС = ÚСYС; (57) Подставим (57) в (56): ÚAYA+ ÚВYВ+ ÚСYС = 0 (58) Фазные напряжения ÚВ и ÚС могут быть выражены через ÚА и заданные линейные напряжения ÚАВ и ÚСА: ÚАВ = ÚА - ÚВ; ÚВ = ÚА - ÚАВ; (59) ÚСА = ÚС – ÚА; ÚС = ÚА + ÚАВ; (60) Подставим (59) и (60) в (58): ÚAYA+ (ÚА – ÚАВ)YВ+ (ÚА + ÚАВ)YС = 0. Отсюда 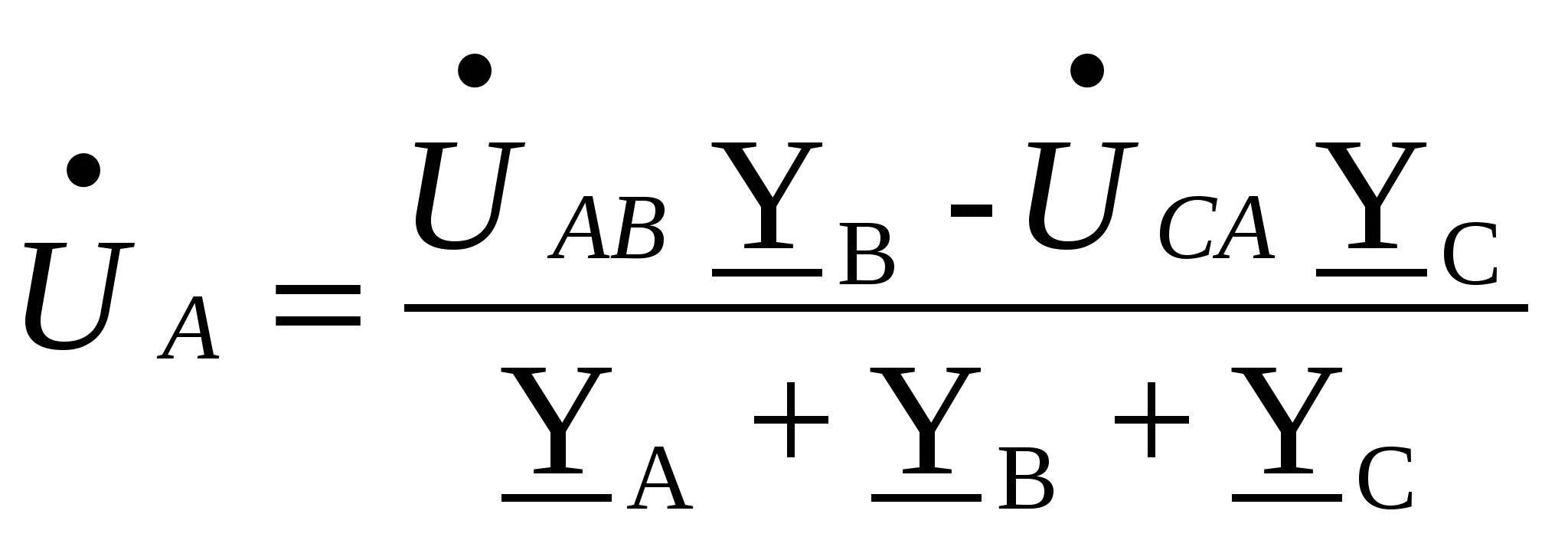 (61) (61)Теперь фазные напряжения ÚА и ÚС выразим через ÚВ и заданные линейные напряжения ÚАВ и ÚВС: ÚАВ = ÚА - ÚВ; ÚА = ÚВ + ÚАВ; (62) ÚВС = ÚВ – ÚС; ÚС = ÚВ - ÚВС; (63) Подставим (62) и (63) в (61): (ÚВ + ÚАВ)YA+ ÚВYВ+ (ÚВ - ÚВС)YС = 0. Отсюда 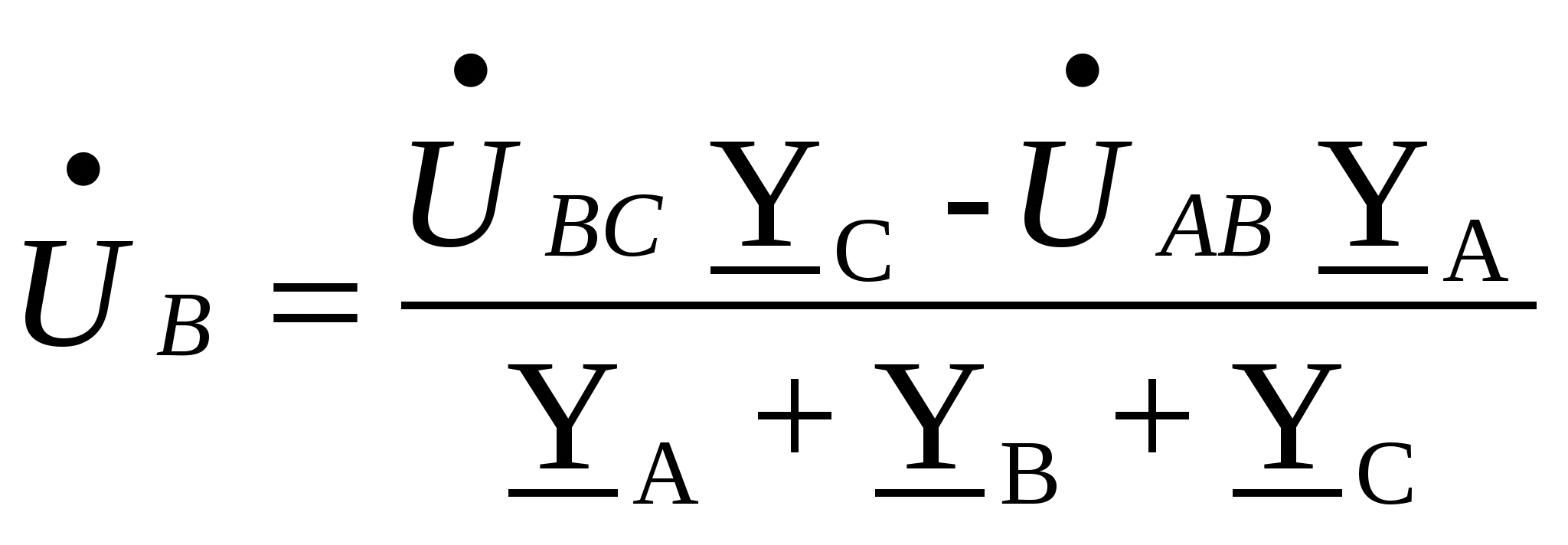 (64) (64)Аналогично выразим ÚА и ÚВ выразим через ÚС и заданные линейные напряжения ÚСА и ÚВС: ÚСА = ÚС – ÚА; ÚА = ÚС – ÚСА; (65) ÚВС = ÚВ – ÚС; ÚВ = ÚС + ÚВС; (66) Подставим (66) и (65) в (64): (ÚС – ÚСА)YA+ (ÚС + ÚВС)YВ+ ÚСYС = 0. Отсюда 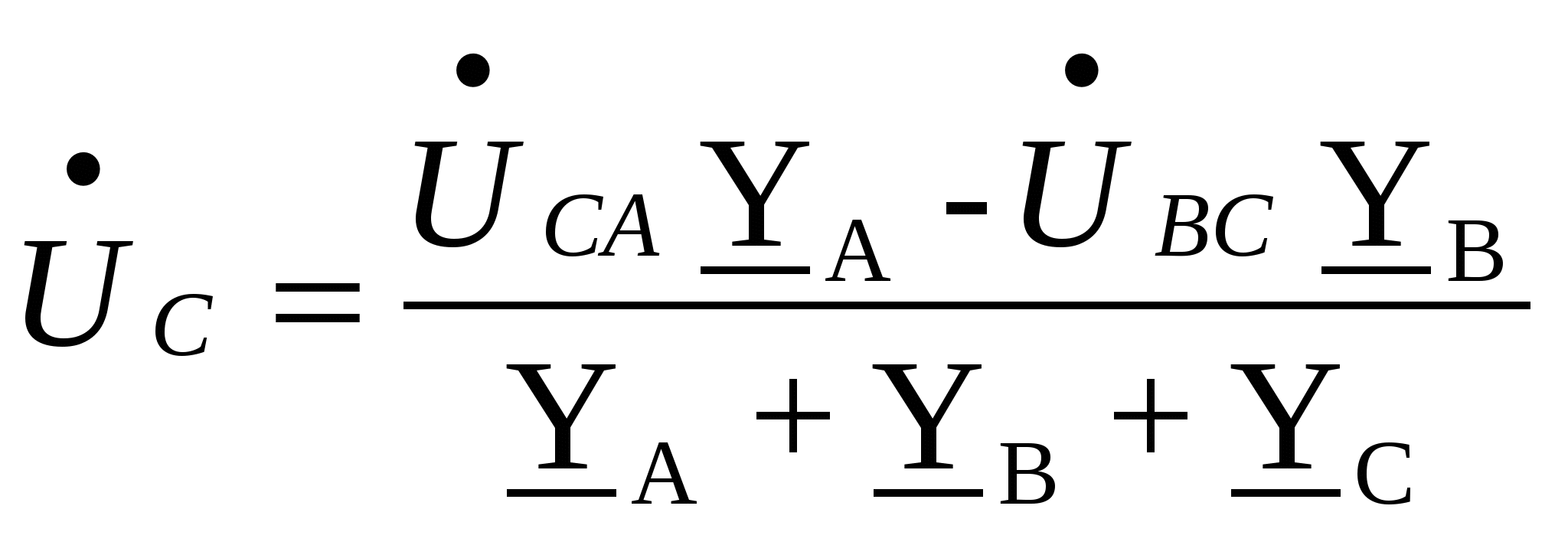 (67) (67)Расчёт схемы, когда нагрузка соединена треугольником и известны линейные напряжения (рис. 23)Сюда подходят схемы соединений треугольник – треугольник и звезда – треугольник. 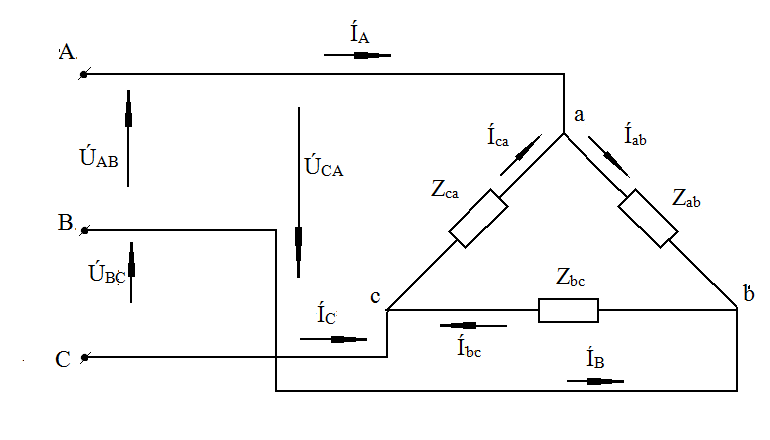 Рис. 23. Электрическая схема Так как заданные линейные напряжения ÚAB, ÚBС, ÚСА напрямую подключаются к сопротивлениям нагрузки Zab, Zbc, Zca, то легко найти фазные токи нагрузок Íab, Íbc, Íca: 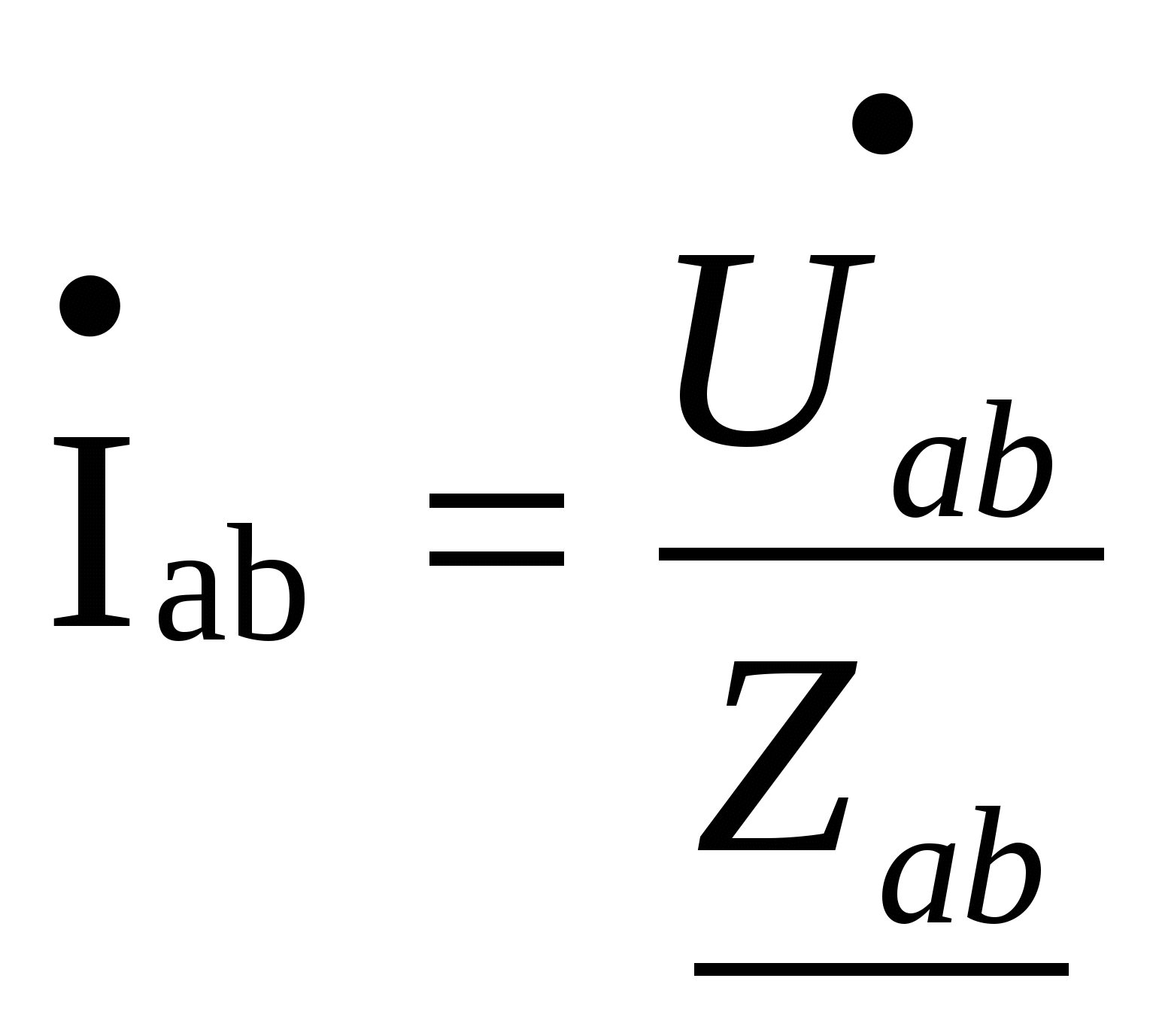 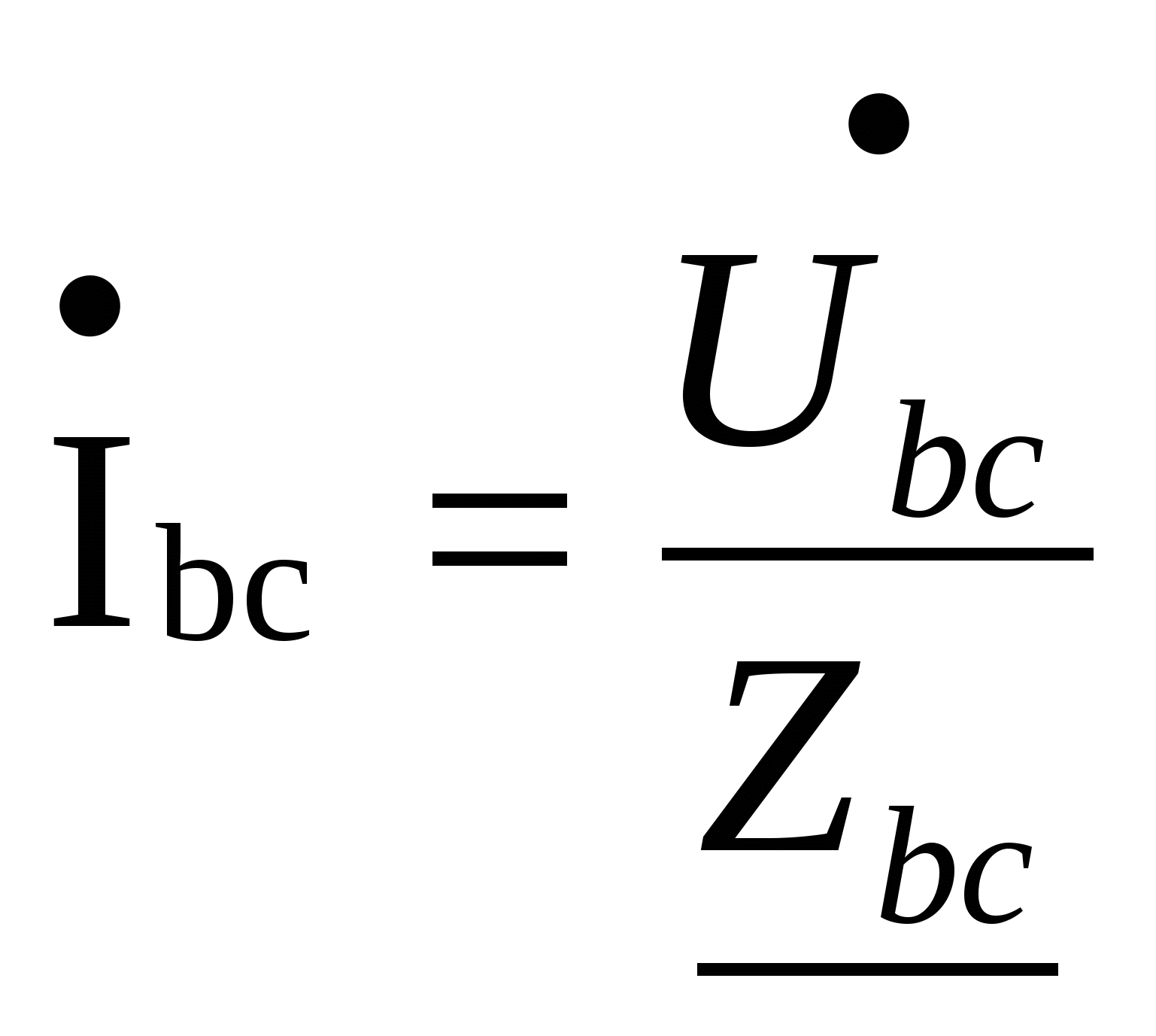 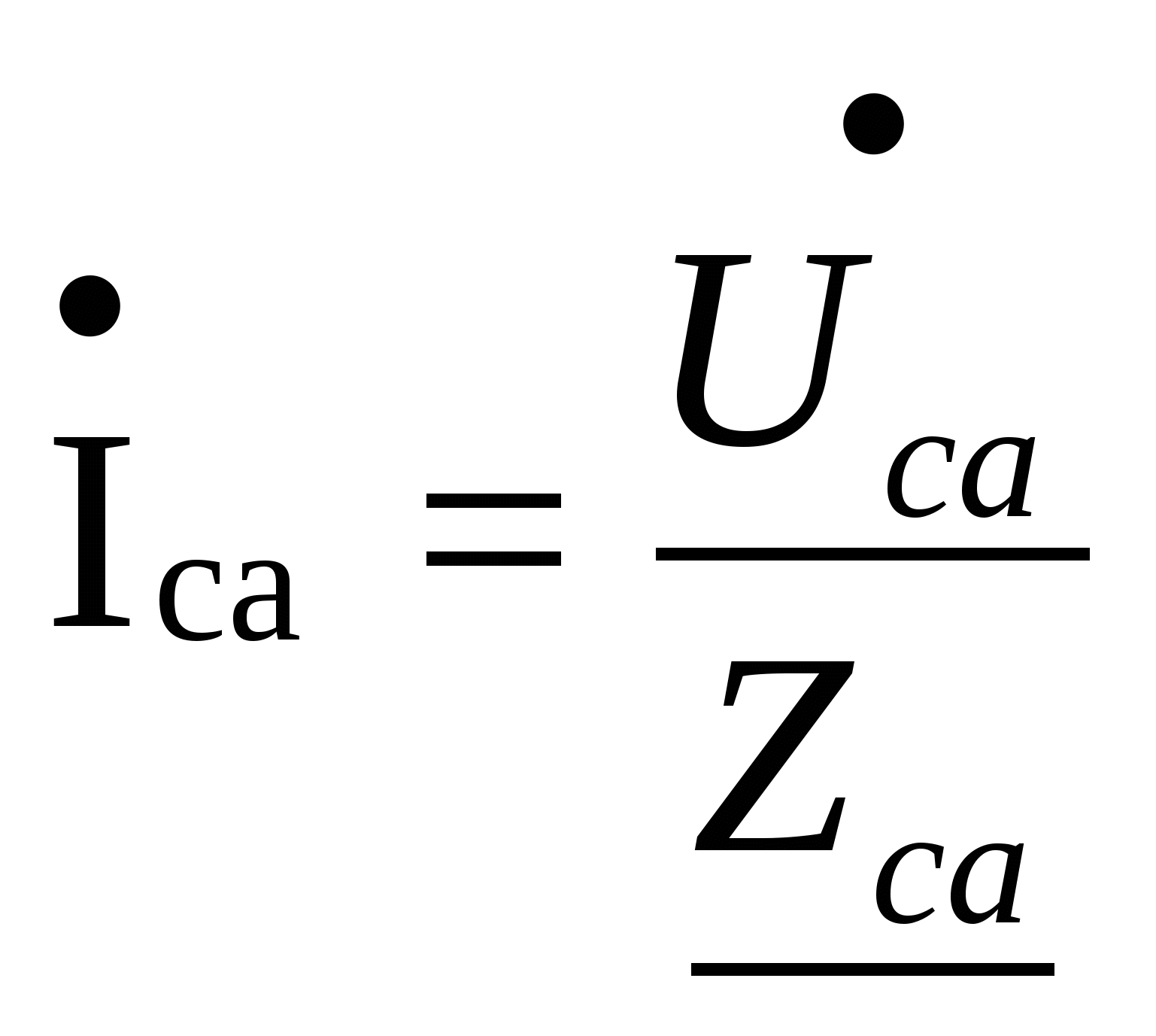 (67) (67)Токи в линейных проводах определяются по первому закону Кирхгофа для узлов a, b, c: ÍА + Ícа - Íab = 0; ÍА = Íаb – Íca; (68) ÍВ + Íаb - Íbc = 0; ÍВ = Íbc – Íab; (69) ÍС + Íbc – Íca = 0; ÍС = Íca – Íbc; (70) Если на выводах несимметричной трёхфазной нагрузки, соединённой треугольником, заданы фазные напряжения источника ÚA, ÚB, ÚC, обмотки которого соединены в звезду, то линейные напряжения на выводах нагрузки находятся как разности соответствующих фазных напряжений: ÚAB = ÚA – ÚВ; ÚBС = ÚB – ÚС; ÚСА = ÚС – ÚС; (71) Далее задача сводится к только что рассматриваемому случаю. Расчёт трёхпроводной трёхфазной схемы, когда в линейных проводах включены сопротивленияКогда между генератором и нагрузкой большое расстояние, то необходимо учитывать сопротивления линейных проводов. Линейные провода обладают активным и индуктивным сопротивлениями. Рассмотрим расчёт схемы соединений треугольник – треугольник (рис. 24). 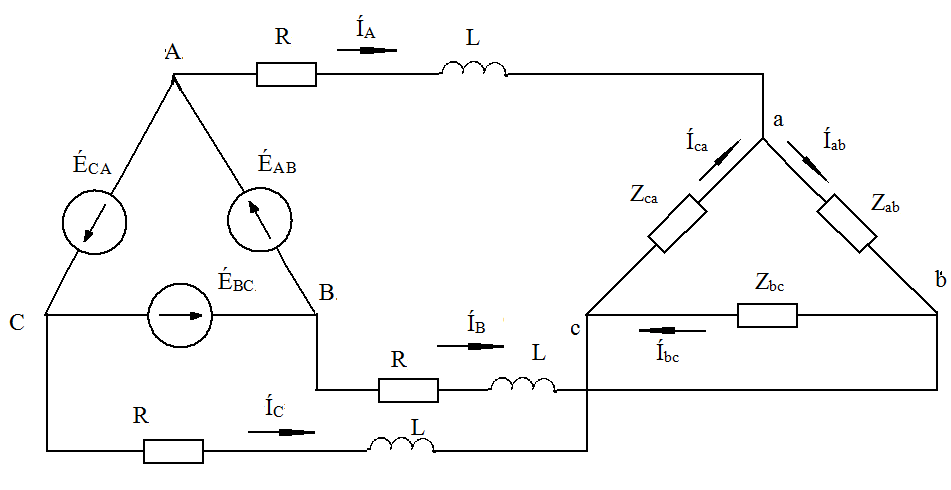 Рис. 24. Схема соединения треугольник - треугольник Будем считать, что нагрузка неравномерная Ни один из выше рассмотренных методов расчёта напрямую не подходит для расчёта данной схемы. Перед расчётом известны все линейные ЭДС генератора Е́АВ, Е́ВС, Е́СА, комплексные сопротивления нагрузок и линейных проводов. Расчёт любой трёхфазной цепи начинается с написания систем трёх линейных и трёх фазных напряжений генератора. Предположим, что Е́АВ = 380В. Что бы не ошибиться, желательно строить векторную диаграмму линейных и фазных напряжений. Вектор Е́АВ направлен по вещественной оси комплексной плоскости (рис. 25) 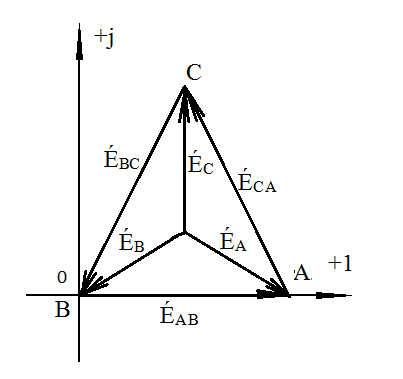 Рис. 25. Векторная диаграмма В 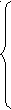 ектор Е́ВС отстаёт от вектора Е́АВ на 120°. В результате получилась следующая система: ектор Е́ВС отстаёт от вектора Е́АВ на 120°. В результате получилась следующая система:Е́АВ = 380 В Е́ВС = 380-j120° = -190 – j329,09 В (72) Е́СА = 380j120° = -190 – j329,09 В Теперь запишем систему трёх фазных ЭДС генератора. Из векторной диаграммы рис. 25 видно, что ЭДС Е́А отстаёт от Е́АВ на 30°. Треугольник линейных ЭДС равносторонний, все углы по 60°. Фазные ЭДС делят эти углы пополам. Кроме того известно, что фазные ЭДС в Поэтому для фазной ЭДС генератора можно записать: Е́А = 220-j30° = 190,526 – j100 В Фазная ЭДС Е́В отстает от Е́А на 120°: Е́В = 220-j150° = -190,526 – j100 В Фазная ЭДС Е́С опережает от Е́А на 120°: Е́С = 220j90° = j220 В Запишем теперь систему трёх фазных ЭДС генератора: Е  ́А = 220-j30° = 190,526 – j100 В ́А = 220-j30° = 190,526 – j100 ВЕ́В = 220-j150° = -190,526 – j100 В (73) Е́С = 220j90° = j220 В Пользуемся ли мы системой трёх линейных ЭДС или трёх фазных ЭДС генератора, потенциалы точек А, В, С одинаковый в обоих случаях. Для расчёта схемы рис. 24 воспользуемся системой трёх фазных ЭДС (73). Далее следует преобразовать треугольник нагрузок в эквивалентную звезду. Обозначим через Za, Zb, Zc сопротивления эквивалентной звезды. Формулы для расчёта точно такие же, как и на постоянном токе, только расчёт ведётся в комплексных числах. На рис. 26 показана эквивалентная схема. 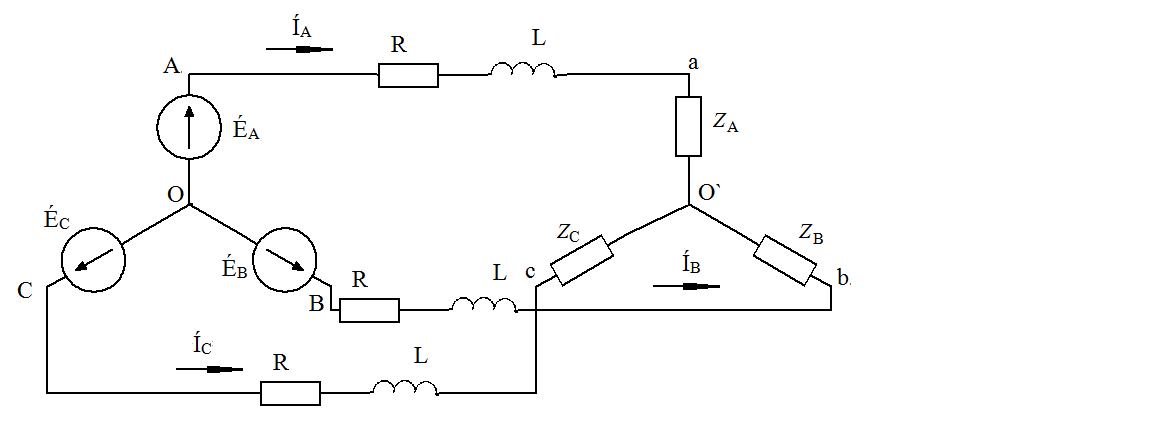 Рис. 26. Эквивалентная схема Эквивалентные сопротивления звезды рассчитываются по следующим формулам: В результате от исходной схемы рис. 24 треугольник – треугольник мы перешли к эквивалентной схеме звезда – звезда без нулевого провода, расчёт которой выше рассмотрен. Эта эквивалентная схема нужна, что бы найти линейные токи ÍA, ÍВ, ÍС. Запишем сначала фазные сопротивления ZА, ZВ, ZС: ZА = R + jXL + Za; (77) ZВ = R + jXL + Zb; (78) ZС = R + jXL + Zc; (79) Далее найдем напряжение ÚO`O: 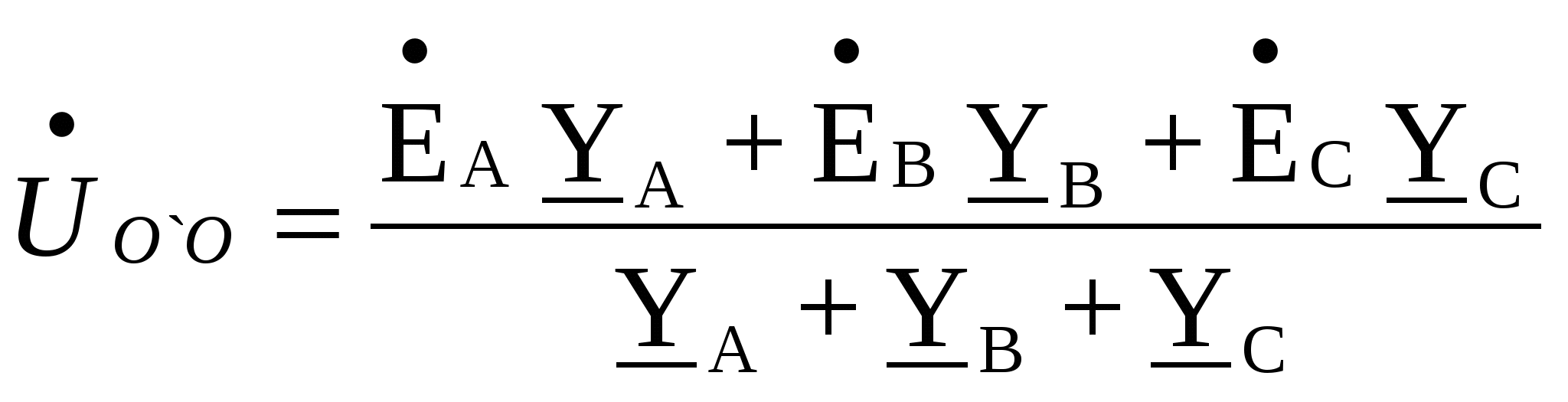 (80) (80)А потом найдем линейные токи: 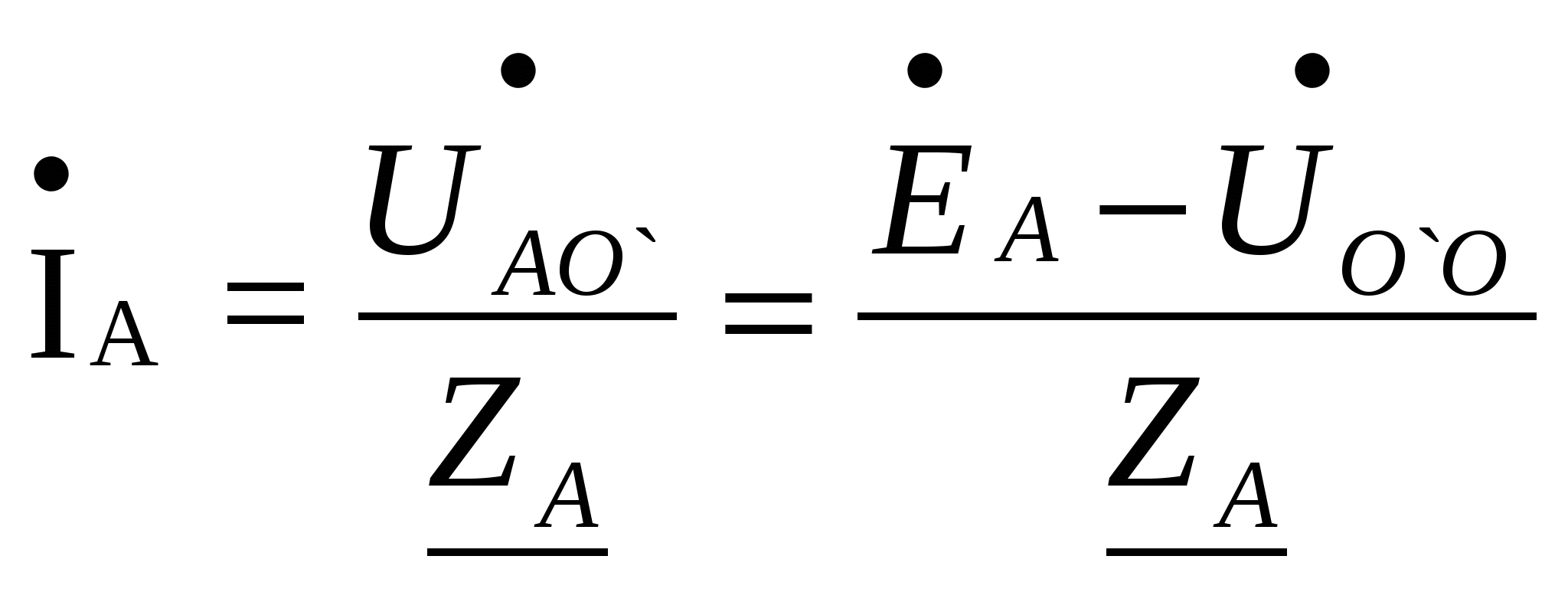 ; (81) ; (81)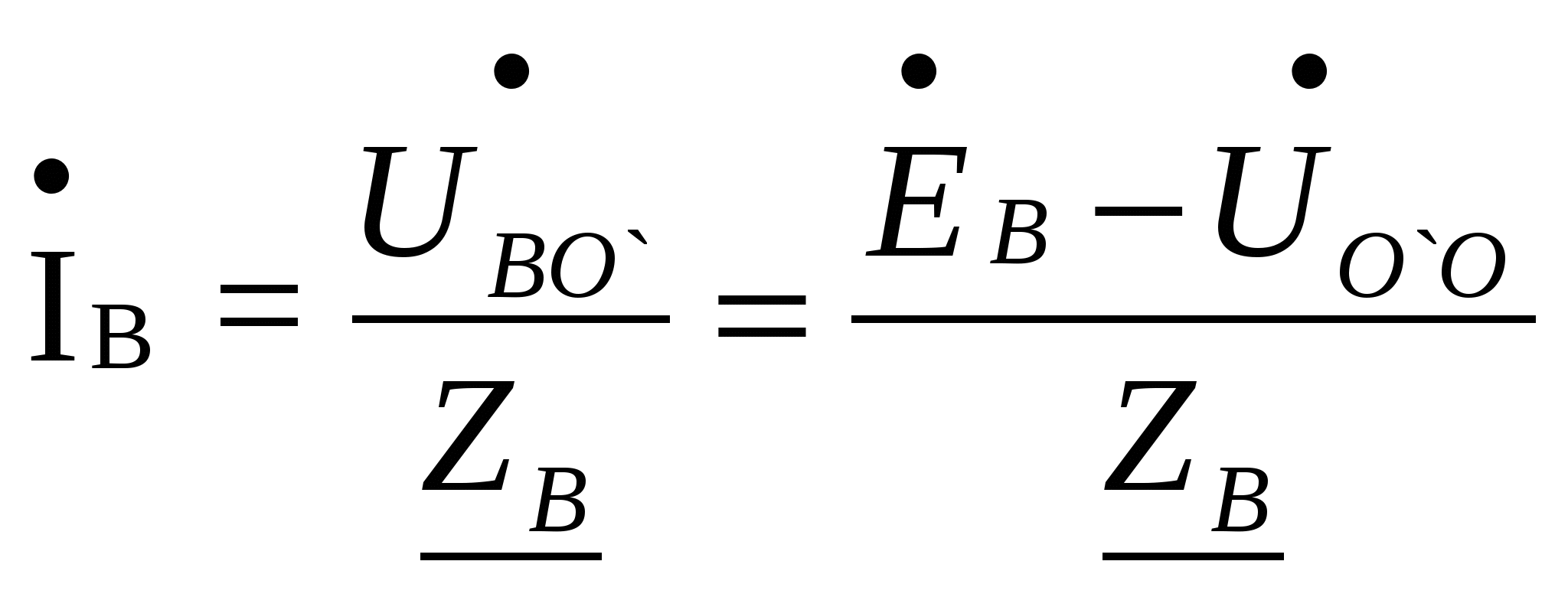 ; (82) ; (82)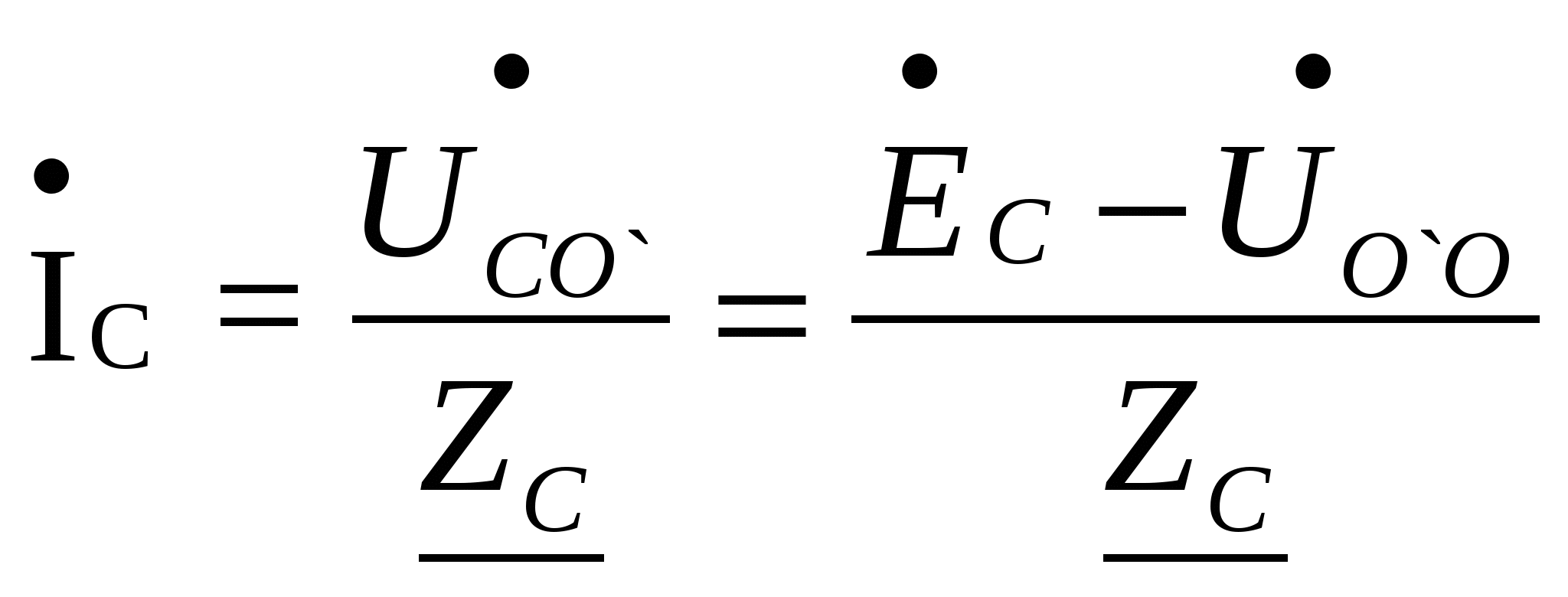 ; (83) ; (83)Теперь надо вернуться к исходной схеме рис. 24 и найти потенциалы точек a, b, c: ϕ́а = Е́А – ÍA(R + jXL) (84) ϕ́b = Е́B – ÍB(R + jXL) (85) ϕ́c = Е́С – ÍС(R + jXL) (86) Далее в схеме рис. 24 найдем фазные токи нагрузок 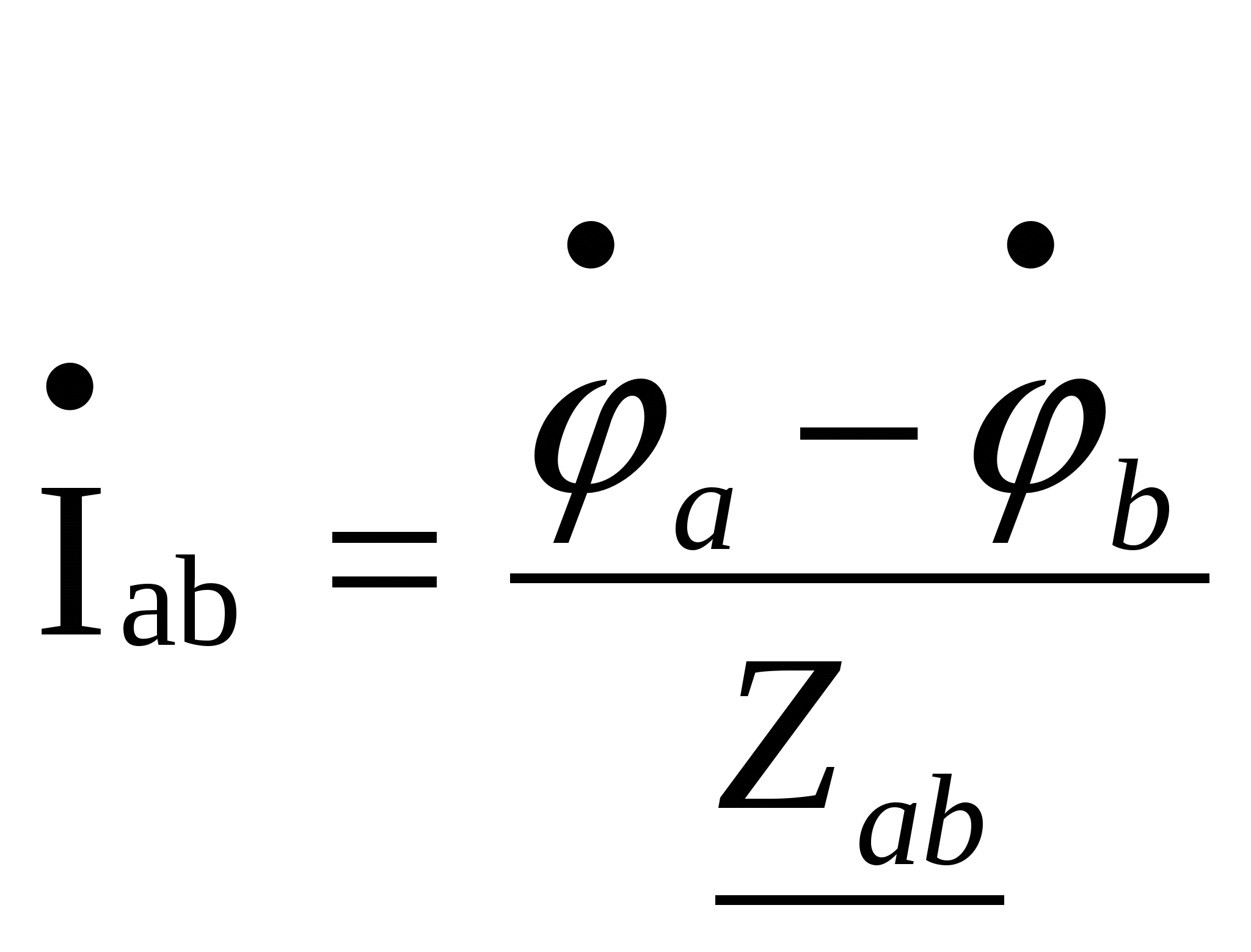 (87) (87)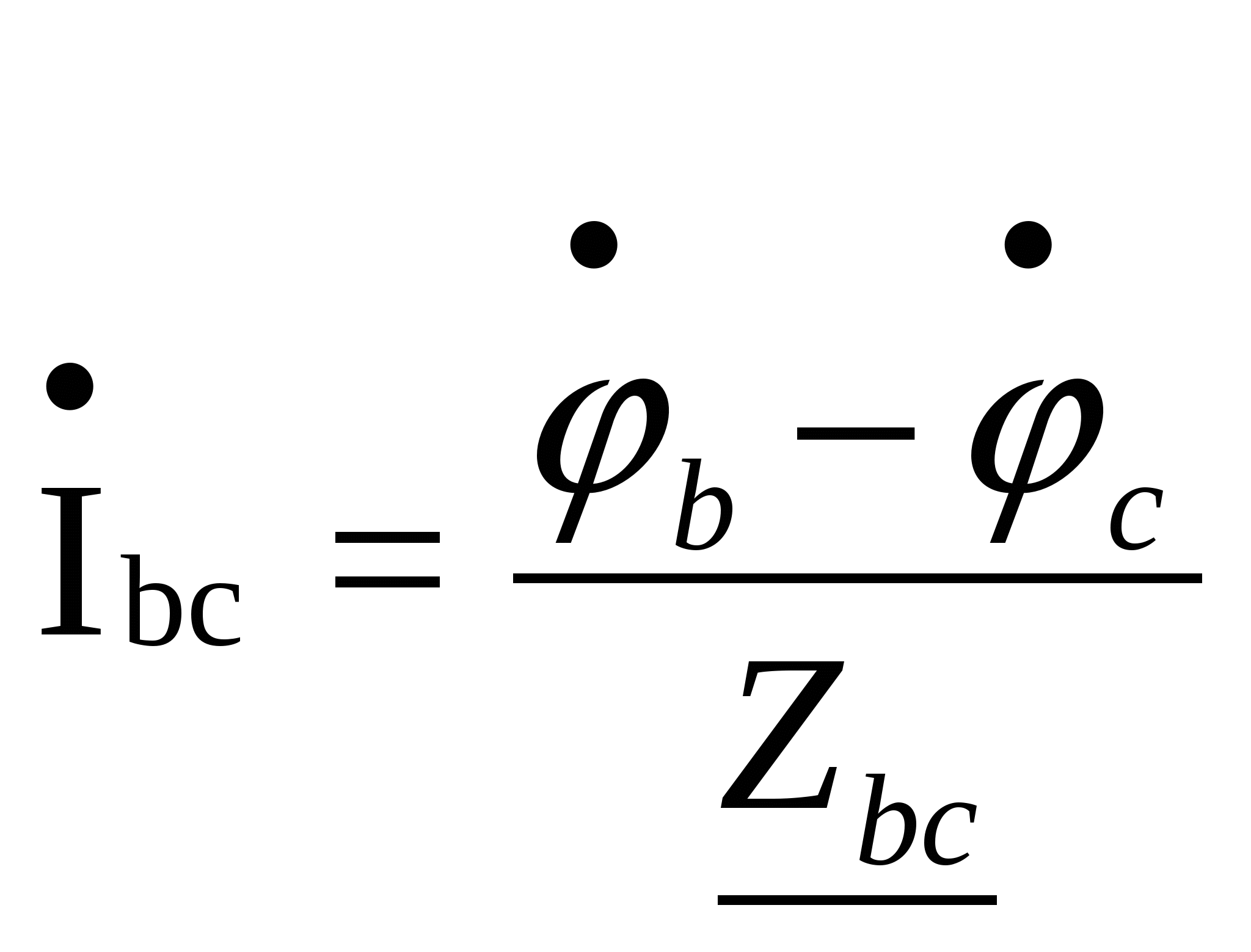 (88) (88)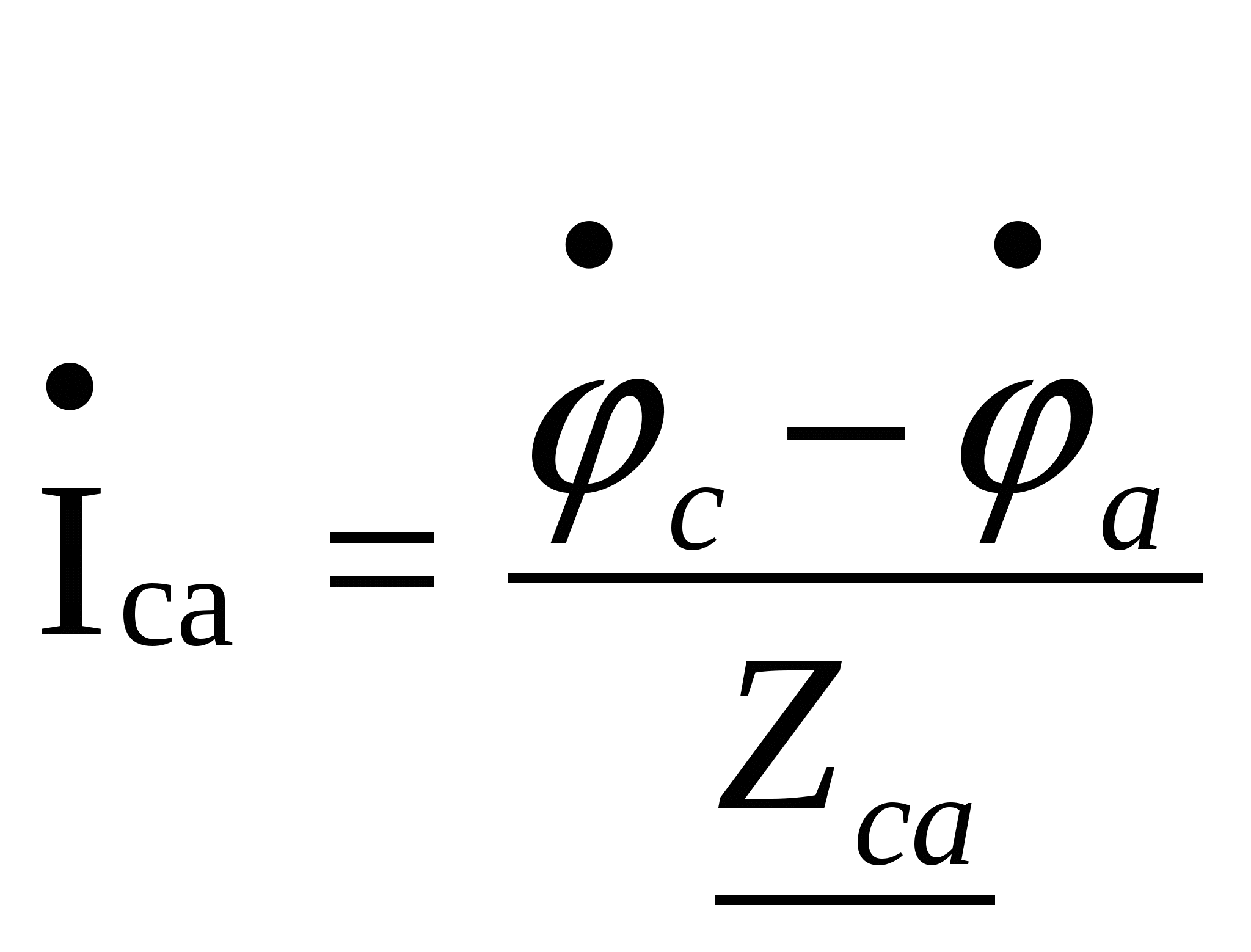 (89) (89)Балансы активных и реактивных мощностей и векторную диаграмму следует делать по исходной схеме рис. 24. Векторная диаграмма начинается с построения системы трёх линейных ЭДС генератора Е́АВ, Е́ВС, Е́СА. Далее следует построить векторы токов, чтобы на диаграмме выполнялись следующие соотношения: ÍA + ÍB + ÍC = 0; (90) ÍА = Íаb – Íca; (91) ÍВ = Íbc – Íab; (92) ÍС = Íca – Íbc; (93) Далее следует посчитать падения напряжений на всех элементах схемы и построить их на диаграмме, чтобы выполнялись следующие соотношения Е́АВ = -ÍBR – ÍBjXL + ÍabZab + ÍAjXL + ÍAR; (94) Е́CВ = -ÍCR – ÍCjXL + ÍbcZbc + ÍBjXL + ÍBR; (95) Е́CA = -ÍAR – ÍAjXL + ÍcaZca + ÍCjXL + ÍCR; (96) Так будет построена полная векторная диаграмма трёхфазной цепи рис. 24. |
