Тренировочный ЕГЭ 2022 Математика, 11 класс, профильный уровень.
1 вариант

Тренировочный ЕГЭ 2022 Математика, 11 класс, профильный уровень.
1 вариант
4.
Найдите  если если 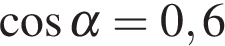 и и 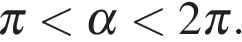
Ответ:_________________
5. Диаметр основания конуса равен 24, а длина образующей равна 13. Найдите высоту конуса.
Ответ:_________________
6. Материальная точка движется прямолинейно по закону 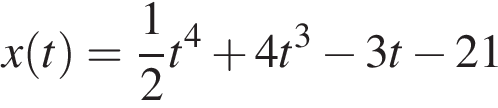 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени  с. с.
Ответ:_________________
7. Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой 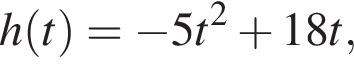 где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров? где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров?
Ответ:_________________
8. Расстояние между городами A и B равно 550 км. Из города A в город B со скоростью 50 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 75 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.
Ответ:_________________
Тренировочный ЕГЭ 2022 Математика, 11 класс, профильный уровень.
1 вариант
11. Найдите наименьшее значение функции  на отрезке на отрезке 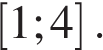
Ответ:____________


12.
а) Решите уравнение 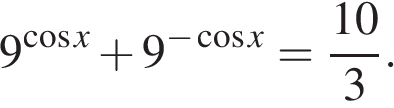
б) Укажите корни этого уравнения, принадлежащие отрезку 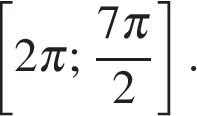
13. В правильном тетраэдре SABC точка M — середина ребра AB, а точка N расположена на ребре SC так, что SN : NC = 3 : 1.
а) Докажите, что плоскости SMC и ANB перпендикулярны.
б) Найдите длину отрезка MN, если длина ребра AB равна 8.
|
Тренировочный ЕГЭ 2022 Математика, 11 класс, профильный уровень.
1 вариант

1.
Найдите корень уравнения 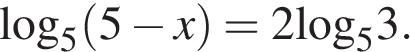
Ответ:___________________
2. На конференцию приехали 6 ученых из Швейцарии, 3 из Болгарии и 6 из Австрии. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что третьим окажется доклад ученого из Болгарии.
Ответ:_________________
3.
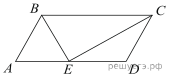
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
Ответ:_________________
Тренировочный ЕГЭ 2022 Математика, 11 класс, профильный уровень.
1 вариант
9.

На рисунке изображён график функции вида 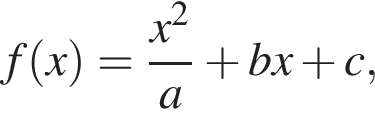 где числа a, b и c — целые. Найдите значение где числа a, b и c — целые. Найдите значение  . .
Ответ:_______________
10. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 85% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 65% яиц высшей категории. Всего высшую категорию получает 80% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Ответ:_______________
Тренировочный ЕГЭ 2022 Математика, 11 класс, профильный уровень.
1 вариант
14. Решите неравенство 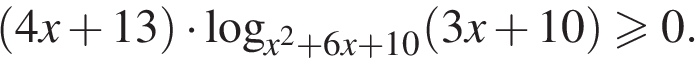
15.
15 декабря планируется взять кредит в банке на 480 тысяч рублей на 27 месяцев. Условия его возврата таковы:
— 1‐го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2‐го по 14 число каждого месяца необходимо выплатить часть долга;
— 15‐го числа первые два месяца и последний долг должен уменьшиться на m тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15‐е число предыдущего месяца на n тысяч рублей.
Найдите отношение 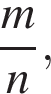 если всего банку будет выплачено 656,4 тысяч рублей? если всего банку будет выплачено 656,4 тысяч рублей?
16. Окружность с центром О1 касается оснований ВС и AD и боковой стороны АВ трапеции ABCD. Окружность с центром O2 касается сторон ВС, CD и AD. Известно, что АВ = 10, ВС = 9, CD = 30, AD = 39.
а) Докажите, что прямая О1О2 параллельна основаниям трапеции АВСD.
б) Найдите О1О2.
17. Найти все значения a, при каждом из которых уравнение
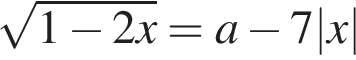
имеет более двух корней.
18. Каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9 по одному записывают на 8 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, −2, −3, 4, −5, 7, −8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться?

|
 Скачать 207.6 Kb.
Скачать 207.6 Kb.