Геом моделирование 2D объектов бис бис (1). У геометрическое моделирование и отображение двухмерных объектов средствами открытой графической библиотеки
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Разработка закона текстурирования При изготовлении текстурного рисунка нужно соблюдать несколько простых правил: размеры холста в пикселях должны быть кратны степени числа 2, то есть годятся размеры 64×64, 64×512, 256×8 и другие подобные; сохранять рисунок нужно в формате bmp в той же папке, где сохраняется графическая программа; нужно учитывать соотношение между пиксельными размерами примитива и текстурного рисунка, то есть для примитива с бо́льшими размерами нужно создавать и больший рисунок. Несоблюдение этих правил приводит к усложнению, а то и к невозможности правильноготекстурирования. Д 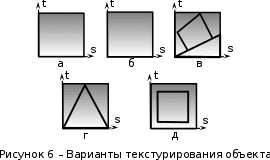 ля выбора закона текстурирования удобно изобразить текстурный рисунок в СКТ и наложить на него проекцию геометрического примитива или целого объекта (зависит от замысла разработчика). В качестве примера можно рассмотреть наложение на объект-стрелку простой текстуры в виде двухцветного поля. На рисунке 6 показаны различные законы текстурирования стрелки. ля выбора закона текстурирования удобно изобразить текстурный рисунок в СКТ и наложить на него проекцию геометрического примитива или целого объекта (зависит от замысла разработчика). В качестве примера можно рассмотреть наложение на объект-стрелку простой текстуры в виде двухцветного поля. На рисунке 6 показаны различные законы текстурирования стрелки.На рисунках 6,а,б,в одна текстура накладывается на весь объект (стрелку), а на рисунках 6,г,д показано раздельное текстурирование частей стрелки, позволяющее разнообразить вид текстурированного объекта. При выборе законов, показанных на рисунках 6,а,б, вид текстурированного объекта понятен из рисунков. Рисунок 6,в показывает только соответствие геометрических и текстурных координат и не свидетельствует об искажении формы стрелки. Стрелка командами рисования будет отображена в соответствии с заданными геометрическими координатами, и форма ее не изменится. А вот текстура будет наложена на нее с искажениями: вдоль одних сторон полигонов текстура будет сжата, вдоль других – растянута. Искажения будут особенно заметны, если текстура будет иметь вид регулярного узора, например, шахматного поля. Выбрав закон наложения текстуры, можно найти текстурные координаты s,tдля всех характерных точек примитивов. В библиотеке OpenGLтекстура независимо от ее размеров располагается в диапазоне от 0 до 1 по каждой координате СКТ. Введя по этим координатам шкалу отсчетов, легко найти текстурные координаты характерных точек объекта по рисунку. Например, для закона текстурирования, сходного с показанным на рисунке 6,б, эти координаты видны из рисунка 7. 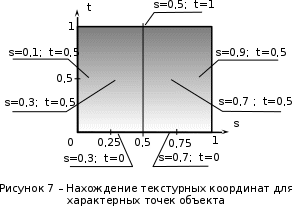 Чтобы проверить, насколько правильно выбран закон наложения текстуры и не приведет ли он к искажению текстуры на изображении, нужно сравнить отношения геометрических и соответствующих им текстурных диапазонов координат для характерных участков объекта. Например, на рисунке 3 длина и высота стрелки в геометрических координатах одинаковы: 0,8 единицы, а в текстурных координатах на рисунке 7 они не одинаковы: 0,8 и 1,0. Это означает, что на изображении текстура будет немного растянута по координате уо стрелки(по рисунку 3). Программирование наложения текстуры По умолчанию примитивы сцены получают однотонную заливку, цвет которой задается командой glColor. Для того чтобы получить возможность накладывать текстуру, нужно воспользоваться уже известной разрешающей командой glEnablecпараметром GL_TEXTURE_2D. Команда вставляется в графическую программу до команд рисования. Тем самым включается режим текстурирования, который действует до тех пор, пока не будет выключен. Выключить (запретить) текстурирование можно в любой момент, применив команду glDisablecтем же параметром GL_TEXTURE_2D, при этом вновь будет включен режим цветной заливки. Таким образом, применяя названные команды в нужные моменты времени, можно отображать различные объекты сцены с текстурированием и с заливкой. Изготовленный в графическом редакторе рисунок должен быть конвертирован графической программой во внутренний формат OpenGL. Для этого в одном из расширений библиотеки (расширении GLAUX) имеются встроенные средства. К ним относится функция auxDIBImageLoad(<параметр>); , параметром которой является текстовая строка, содержащая имя файла рисунка с расширением bmp и путь к файлу. Функция выполняет конвертирование рисунка, размещает его в некоторой области памяти с определенной структурой и возвращает указатель на эту область. Переменная-указатель описывается в программе как указатель на тип AUX_RGBImageRec, который задает структуру памяти текстуры. Указанная функция хорошо работает в программах, написанных на С-подобных языках. В программах, написанных в среде Delphi, для конвертации с успехом может быть применен свободно распространяемый программный модуль BMP.pas,автором которого является голландский программист Ян Хорн. Модуль преобразует рисунки формата bmp в текстурные образцы библиотеки OpenGL. Для использования его нужно присоединить к программе в разделе uses. В состав модуля ВМР входит процедура конвертации форматов LoadTexture(‘<имя рисунка и путь>’,<имя текстурного образца>); , имеющая два параметра. Первый – текстовая строка в апострофах, которая содержит путь к файлу рисунка (диск, каталог, подкаталог,…) и его имя с расширением bmp. Если рисунок сохранен в той же папке, где хранится программа, путь указывать не нужно. Второй параметр команды – это имя текстуры (текстурного образца), в которую конвертируется рисунок. В качестве текстурных имен в OpenGL используются целые числа, поэтому в программе нужно ввести переменную целого типа (встроенного типа OpenGLGLuint – беззнаковое целое – или типа word, поддерживаемого средой Delphi). Если рисунок сохранен в одной папке с программой и его имя TexRis1, а имя текстуры TexName1, то процедура конвертации вызывается так: LoadTexture(‘TexRis1.bmp’,TexName1); . После создания текстуры она становится текущей, то есть может тут же использоваться для текстурирования. Если в сцене несколько объектов имеют различные текстуры, процедуру конвертирования приходится применять неоднократно.Это можно сделать двумя способами. Во-первых, процедуру конвертации можно вызывать перед текстурированием каждого очередного объекта, то есть действовать по схеме: конвертация текстуры 1, наложение текстуры 1, конвертация текстуры 2, наложение текстуры 2 и так далее. В этом случае в программе достаточно иметь одну переменную для имени текстуры, и эта переменная поочередно будет связываться со всеми текстурными образцами, которые будут заноситься в одну и ту же область памяти. Такой вариант прост, но несколько «тормозит» программу, так как конвертирование рисунков (особенно, большого размера) в ходе рисования требует дополнительного времени. Второй вариант конвертации грамотнее и эффективнее.Он предполагает, что все текстуры заготавливаются заранее и получают свои уникальные имена. Для этого процедуры конвертации вызываются в начале программы с различными значениями второго параметра. Теперь для того, чтобы выбрать необходимую для некоторого объекта текстуру, например, с именем TexName, ее надо перед наложением сделать текущей. Для этого служит следующая команда библиотеки OpenGL: glBindTexture(GL_TEXTURE_2D,TexName); . В этом случае возникает такая схема текстурирования: конвертация текстуры 1, конвертация текстуры 2 и так далее, вызов текстуры 1 в качестве текущей, наложение текстуры 1, вызов текстуры 2 в качестве текущей, наложение текстуры 2 и так далее. Следует отметить, что для программы, написанной в среде Delphi, команда glBindTexture является внешней процедурой, описание которой содержится в файле библиотеки opengl32.dll. Поэтому для использования команды эта процедура должна быть упомянута в разделе программы implementation: procedureglBindTexture(target: GLenum; texture: GLuint); stdcall; external opengl32; . ЗдесьGLenumиGLuint – встроенныетипыданныхбиблиотекиOpenGL, вDelphiимсоответствуеттипCardinal. Когда текстурный образец сделан текущим, можно приступать к непосредственному наложению текстуры на примитивы. Для этого нужно каждой характерной точке примитива сопоставить ее текстурные координаты. Геометрические координаты характерных вершин задаются командами glVertex. Для привязки к ним текстурных координат перед каждой командой glVertex вставляется команда glTexCoord2f(s,t); , вкоторойs и t – соответствующие текстурные координаты, заданные константами или переменными вещественного (float) типа. В качестве примера ниже приведен фрагмент программы, рисующий текстурированный треугольник стрелки. Геометрические координаты вершин треугольника взяты из таблицы 2 с учетом рисунка 3, текстурные – с рисунка 7. glEnable(GL_TEXTURE_2D); LoadTexture(‘TexRis1.bmp’,TexName1); //задание режима наложения текстуры glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER,GL_LINEAR); glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER,GL_LINEAR); //задание белого цвета «подложки» текстуры glColor3f(1.0,1.0,1.0); //рисование с текстурированием glBegin(GL_TRIANGLES); glTexCoord2f(0.1,0.5); glVertex3f(0.0,0.4,0.0); glTexCoord2f(0.5,1.0); glVertex3f(0.4,0.0,0.0); glTexCoord2f(0.9,0.5); glVertex3f(0.0,-0.4,0.0); glEnd(); Некоторыекомандывприведенномфрагментенуждаютсявпояснениях. Как уже отмечалось, текстура может накладываться на примитив со сжатием или с растяжением. В первом случае на изображении могут пропасть мелкие элементы, во втором может появиться ступенчатость наклонных линий. Для повышения качества текстурирования применяют различные фильтры. Их суть в том, что цветояркость каждого пикселя, принадлежащего примитиву, определяется не одним текселем текстуры, а находится с помощью усреднения цветояркости нескольких текселей из некоторой окрестности. Закон усреднения может быть различным. Чем он сложнее, тем выше качество изображения, но ниже скорость его обработки. Оптимальным можно считать линейный закон усреднения (GL_LINEAR), который и задается в приведенном фрагменте программы командами glTexParameter для случая растяжения(MAG_FILTER)и сжатия(MIN_FILTER) текстуры. Если в программе перед текстурированием командой glColor задан цвет пера, отличный от белого, то при текстурировании примитива произойдет смешивание цветов текстуры и цветовой «подложки» (заливки) примитива. Такой режим наложения текстуры установлен в библиотеке OpenGLпо умолчанию. В результате цветовая гамма текстуры на изображении окажется измененной. Этот эффект можно использовать для повышения разнообразия цветовых решений. Если же требуется, не меняя настроек, получить на изображении текстуру в исходном виде, то перед текстурированием следует задать белый цвет пера, что и сделано в приведенном фрагменте программы. Режим наложения текстуры может быть изменен командойglTexEnv. Например, следующий вариант ее написания включает режим замены цвета заливки примитива цветами текстуры: glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE,GL_REPLACE); . Дополнительные возможности текстурирования Как уже отмечалось, текстурные координаты s, t в СКТ лежат в диапазоне от 0 до 1. Однако это не означает, что параметры команды glTexCoord могут лежать только в этом диапазоне. Задавая их величину большей единицы или отрицательной, можно реализовать дополнительные возможности текстурирования. Если, например, наложить текстуру на четырехугольник следующим набором команд: glBegin(GL_QUADS); glTexCoord2f(0.0,0.0); glVertex2f(0.0,0.0); glTexCoord2f(0.0,1.0); glVertex2f(0.0,0.5); glTexCoord2f(5.0,1.0); glVertex2f(0.5,0.5); glTexCoord2f(5.0,0.0); glVertex2f(0.5,0.0); glEnd(); то произойдет пятикратное наложение (размножение) текстуры в горизонтальном направлении. Размножением текстуры часто пользуются при отображении протяженных поверхностей с хаотичным рисунком (камни, песок, трава). Применение размножения в этом случае позволяет раскрасить поверхность больших размеров, используя небольшую текстуру, чем достигается экономия памяти вычислительной системы. Использование отрицательных значений текстурных координат позволяет накладывать текстуру в обратном направлении, то есть в зеркальном отражении. Возможности и логика размножения и зеркального отражения текстуры будут более понятными, если принять образ размещения текстуры (на примере цветка) в СКТ в соответствии с рисунком 8. 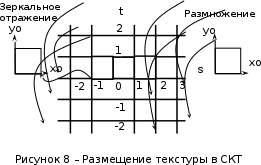 Стрелками на рисунке 8 показано установление соответствия между геометрическими и текстурными координатами. Следует отметить, что при текстурировании можно задавать дробные значения текстурных координат. Возникающий при этом эффект можно понять, пользуясь рисунком, аналогичным рисунку 8. Задание по текстурированию для самостоятельного выполнения (углубленное задание) 1) Создать текстурный фон сцены в виде нескольких разноцветных кругов. Подсказка: текстура не может существовать сама по себе, она должна быть наложена на какой-либо геометрический примитив. 2) Наложить текстуру на квадрат в соответствии с рисунком 9. 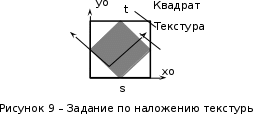 ОТОБРАЖЕНИЕ ДИНАМИЧЕСКИХ СЦЕН 5.1 Описание динамики объектов Динамика объекта может проявляться в виде изменения его размеров или местоположения на экране без изменения формы, изменения формы объекта без изменения его местоположения и в виде одновременного изменения упомянутых параметров в разных сочетаниях. Любая динамика привязывается ко времени. Сутью ее программирования является циклическая перерисовка объекта с изменением его геометрических параметров в каждом цикле. Изменение местоположения объекта Геометрические преобразования объектов, как известно, задаются командами glTranslate, glRotate, glScale. Их параметры при каждой перерисовке могут меняться с постоянным приращением, например, для сдвига x:=x+dx; для поворота ALFA:=ALFA+dALFA; для масштабирования kx:=kx+dkx. Команды геометрических преобразований применяются ко всей ОСК. При использовании приращений неизменной величины закон преобразований будет линейным. Более интересным случаем является нелинейная динамика, при которой параметры команд должны вычисляться. Например, на практике часто применяют круговую или, в общем случае, эллиптическую замкнутую траекторию движения объектов. Движение объекта по эллиптической траектории может происходить без поворота («параллельно самому себе») и с поворотом. Образно можно представить себе первый вариант на примере движения кабины колеса обозрения, а второй вариант – на примере картинки, приклеенной к концу секундной стрелки часов. Для реализации первого варианта нужно циклически вычислять координаты точек, принадлежащих эллиптической траектории, и использовать их как параметры команды сдвига. Сдвиг должен применяться ко всей ОСК, в которой описан объект. При этом не надо забывать, что команда сдвига в OpenGLработает по приращениям. Со школы известно каноническое уравнение эллипса с центром в начале координат 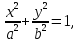 где aи b– полуоси эллипса. Для применения в компьютерной графике оно весьма неудобно. Действительно, приняв за аргумент координату х и изменяя ее в интервале от (–a) до (+a), получим 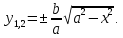 Для каждого значения х нужно найти два значения у: у1 и у2, так как эллипс описывается неоднозначной квадратической функцией. Тогда для последовательного перебора точек эллиптической траектории придется сначала с постоянным шагом изменять х от (-а) до (+а) и вычислять у1, а затем – изменять х от (+а) до (-а) и вычислять у2. Алгоритм получается усложненным, а точки на траектории будут расставлены неравномерно. Недостатки можно минимизировать, используя параметрическое уравнение эллипса: 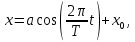 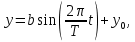 где x0, y0 – координаты центра эллипса; t – параметр-время, который изменяется в интервале от 0 доT; T – длительность однократного прохождения объектом эллиптической траектории. В качестве параметра t здесь выступает время, тогда приведенные выражения получают понятный смысл. Они описывают поведение (изменение) координат х и у во времени.Траекторию нужно разделить на некоторое количество N шагов и установить временной интервалT, за который траектория будет пройдена. Тогда удобно принять 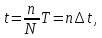 где n – номер шага по траектории (n=0,…,N); Δt – длительность шага (Δt=T/N). Если объект движется по эллиптической траектории с поворотом, нужно после команды сдвига использовать команду поворота. Угол поворота в общем случае нужно вычислять, однако при круговой траектории это сделать просто: он равен 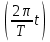 . И более того, в случае круговой траектории с центром в точке (х0,у0) и радиусом R алгоритм отображения упрощается. В очередном цикле отображения нужно сначала выполнить сдвиг ОСК в точку (х0,у0), затем повернуть ОСК на угол . И более того, в случае круговой траектории с центром в точке (х0,у0) и радиусом R алгоритм отображения упрощается. В очередном цикле отображения нужно сначала выполнить сдвиг ОСК в точку (х0,у0), затем повернуть ОСК на угол 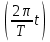 , а затем сдвинуть ее по оси уо на величину радиуса R. Логику алгоритма легко понять, нарисовав результаты перечисленных преобразований. , а затем сдвинуть ее по оси уо на величину радиуса R. Логику алгоритма легко понять, нарисовав результаты перечисленных преобразований.Более общим случаем динамики объектов является их движение по траектории произвольной формы. В качестве примера можно рассмотреть движение объекта по криволинейной траектории, показанной на рисунке 10. 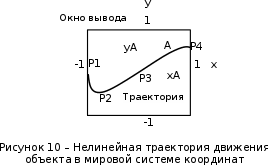 Подобная траектория не может иметь более двух экстремумов и, следовательно, описывается уравнением третьей степени: 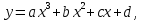 где a, b, c, d – коэффициенты формы, определяющие своеобразие кривой. Для каждого значения х кривая имеет одно значение у, то есть одну точку. Например, для х=хА это у=уА, что соответствует точке А. В этом случае коэффициенты формы можно найти, наложив ограничения на 4 точки кривой. Пусть это точки Р1,…,Р4, координаты которых заданы разработчиком так, как показано в таблице 4. Таблица 4 – Координаты характерных точек траектории
Тогда,подставляя координаты этих точек в уравнение траектории, можно составить систему из четырех уравнений с четырьмя неизвестными коэффициентами формы: 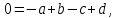 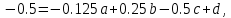 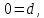 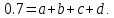 Решив систему любым известным методом, можно найти численные значения коэффициентов формы и, подставив их в уравнение траектории, получить расчетное выражение. Теперь в графической программе нужно организовать изменение аргумента х с некоторым шагом. Каждый шаг привязывается к отсчету системного времени (обращение к системному таймеру выполняется своими средствами в каждой среде программирования). Вычисленные значения величин х и у передаются в команду сдвига в качестве параметров. Более сложным случаем является движение объекта по траектории, описываемой многозначной функцией. Для нее каждому значению аргумента х соответствует несколько значений у, как это показано на рисунке 11. 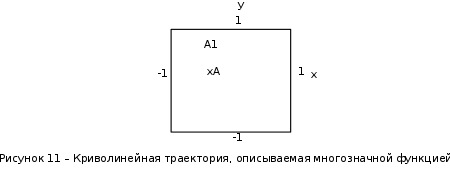 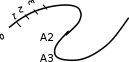 Здесь придется применить параметрическое описание траектории, например, такое: 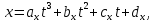 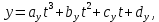 где t – параметр-время; ax,…,dy– коэффициенты формы. Для нахождения коэффициентов формы можно применить уже знакомый прием: исходя из желаемого вида траектории, задать на ней 4 характерные точки, для которых найти координаты xi, yi(i=1,…,4). Точки должны быть привязаны к значениям ti, то есть моментам времени, в которые они будут достигнуты; подставляя координаты и значения времени в параметрическое описание траектории, получить две системы из четырех уравнений с четырьмя неизвестными каждая. При этом в первой системе уравнений будут использоваться только xi, а во второй – только yi; решив системы уравнений, найти значения коэффициентов формы для описания каждой координаты траектории. При программной реализации траектории шаги по ней нужно привязать к отсчетам системного таймера, расставленным с интервалом Δt. Вся траектория должна составлять Nшагов. При отладке программы часто возникает необходимость изменить форму траектории. Даже если эти изменения невелики, они вызывают необходимость пересчета всех коэффициентов формы. Применив другую форму описания траектории, можно существенно облегчить процесс ее редактирования. Речь идет о кривой Безье, предложенной французским специалистом по компьютерной графике Пьером Безье (PierreÉtienneBézier). В форме Безье траектория описывается четырьмя характерными (опорными) точками Р1, Р2,Р3,Р4, две из которых (Р1, Р4) принадлежат концам кривой, а две другие (Р2, Р3) – лежат на касательных, проведенных через конечные точки, и задают изгиб кривой. Кривая Безье показана на рисунке 12, а ее математическое описание в параметрической форме имеет вид 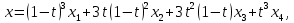 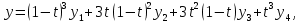 где х1,…,х4 и у1,…,у4– координаты четырех опорных точек; t 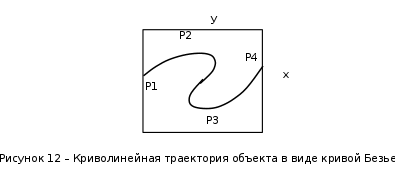 – параметр, изменяющийся в диапазоне от 0 до 1. – параметр, изменяющийся в диапазоне от 0 до 1.Выбрать Р1 и Р4 просто: это начало и конец желаемой траектории. Для нахождения Р2 и Р3 нужно знать значения производных 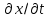 и и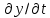 в начальной и конечной точках. Тогда в начальной и конечной точках. Тогда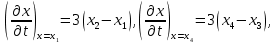 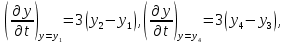 откуда можно найти координаты точек Р2, Р3. Найти значения частных производных по t сложно, поэтому лучше применить простой прием нахождения координат точек Р2, Р3. Желаемую траекторию нужно нарисовать в МСК, ориентировочно провести касательные к кривой в ее начальной и конечной точках и поставить на них точки Р2 и Р3. При расстановке этих точек следует пользоваться простым правилом: чем сильнее вытянута траектория в направлении касательной, тем дальше от крайней точки Р1 (Р4) должна стоять на этой касательной средняя опорная точка Р2 (Р3). Получив в результате графических построений координаты опорных точек, их надо подставить в описание кривой Безье. Теперь эти выражения можно использовать для нахождения промежуточных точек траектории. Для редактирования формы траектории достаточно изменить координаты опорных точек и посмотреть на результат. Изменение формы объекта Для изменения формы объекта нужно управлять положением его отдельных вершин. В качестве примера можно рассмотреть превращение треугольника в квадрат, его иллюстрирует рисунок 13. В процессе превращения происходит изменение положения вершин треугольника. Поскольку число вершин у квадрата на единицу больше, чем у треугольника, в треугольнике нужно заранее предусмотреть дополнительную вершину (на рисунке 13 это Р2), которая станет еще одной вершиной квадрата (S2). Изменение положения вершин показано на рисунке 13 стрелками. Для описания перемещения вершины Рiв новое положение Si удобно применить линейную интерполяцию. 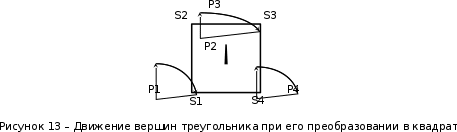 Текущие координаты новой вершины вычисляются по интерполяционным выражениям 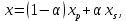 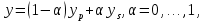 где α – интерполяционный коэффициент; xp, yp – координаты вершины Рi; xs, ys – координаты вершины Si. При α=0 вершина находится в положении Рi, при α=1 – в положении Si, при 1>α>0 вершина находится в некотором среднем положении на прямой, соединяющей Рi и Si. Подставив значение α в зависимость от времени t, можно записать: 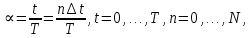 где T– запланированная длительность перехода вершины из положения Рiв положение Si; n – номер шага по траектории перехода вершины от Рi к Si; Δt – длительность шага; N – запланированное число шагов перехода вершины от Рi к Si. Чем меньше Δt и больше N, тем плавнее будет двигаться вершина. На практике следует выбирать Δt≤0,03 с. Число N зависит от расстояния перехода и выбирается так, чтобы длина одного шага на экране была соизмерима с размером пикселя. Координаты вершин, вычисляемые в цикле по интерполяционным выражениям, используются в качестве параметров команд glVertex. Изменение формы объектов можно получить, применив команду масштабирования glScaleс неодинаковыми масштабными коэффициентами.Процесс деформации будет плавным, если масштабные коэффициенты вычислять в цикле, например, по интерполяционным выражениям 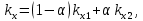 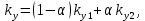 где kx1,ky1 – начальные, а kx2,ky2– конечные значения масштабных коэффициентов. Коэффициент интерполяции зависит от времени и определяется так, как было показано для изменения положения вершин. 5.2 Программирование динамики графических объектов Динамические изображения выводятся на экран по фазам движения. Если частота смены фаз достаточно велика(больше 30 Гц), наблюдатель видит плавную динамику. Для формирования динамических изображений требуются два буфера кадра, в вычислительной системе они называются задним и передним буферами. Пока в заднем буфере накапливается очередная фаза динамики изображения, из переднего на экран выводится изображение предыдущей фазы. После накопления в заднем буфере очередной фазы она быстро переписывается в передний буфер, и процесс повторяется. Если же использовать один буфер кадра, он попеременно должен работать на создание изображения и считывание его на экран, что снижает цветовую насыщенность изображения, а то и делает его мелькающим. По умолчанию в вычислительной системе работает именно один буфер – задний. Чтобы использовать двойную буферизацию, нужно в программе по окончании рисования инициировать подключение переднего буфера. Это делает процедура SwapBuffers; или команда расширения GLUT glutSwapBuffers();. Для отображения объекта, движущегося по некоторой траектории, его экранные координаты циклически пересчитываются и используются в команде сдвига glTranslate. При этом нужно помнить, что командой сдвига задаются не экранные координаты объекта, а расстояния его перемещения. Каждый следующий сдвиг выполняется относительно предыдущего положения объекта. Это означает, что каждый раз для перемещения объекта в очередную точку траектории нужно либо вычислять приращения координат объекта относительно предыдущего положения, либо «сбрасывать» результат предыдущего сдвига и вычислять новые координаты объекта относительно его исходного положения. Второй вариант легче реализовать: для этого достаточно воспользоваться уже известными командами glPopMatrix, glPushMatrix. То же можно сказать и про работу с командой поворота glRotate. Приложение А. Структура типовой графической программы и назначение ее компонентов «Заготовка» графической программы, написанной в среде Delphi unitTest; interface uses Windows, Messages, Forms, Dialogs, Classes, Controls, ExtCtrls, StdCtrls,OpenGL, BMP; type TForm1 = class(TForm) procedureFormPaint(Sender: TObject); procedureFormCreate(Sender: TObject); procedureFormDestroy(Sender: TObject); private hrc: HGLRC; end; var Form1: TForm1; implementation {$R *.DFM} procedureglBindTexture(target: GLenum; texture: GLuint); stdcall; external opengl32; //===========================Рисованиеокна======================= procedure TForm1.FormPaint(Sender: TObject); begin wglMakeCurrent(Canvas.Handle, hrc); glMatrixMode(GL_PROJECTION); glLoadIdentity(); glOrtho(-1.0,1.0,-1.0,1.0,-1.0,1.0); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); //================Здесьбудутрисоватьстуденты=========== glClearColor(0.8,0.8,0.8,1.0); // см. подраздел 2.4 glClear(GL_COLOR_BUFFER_BIT); glEnable(GL_DEPTH_TEST); //см. подраздел 3.5 glClear(GL_DEPTH_BUFFER_BIT); glEnable(GL_TEXTURE_2D); // см. подраздел 4.3 //============================================================= wglMakeCurrent (0, 0); end; //================ Определениеформатапикселя ================ procedureSetDCPixelFormat (hdc: HDC); var pfd: TPixelFormatDescriptor; nPixelFormat: Integer; begin FillChar (pfd, SizeOf(pfd), 0); pfd.dwFlags := PFD_DRAW_TO_WINDOW or PFD_SUPPORT_OPENGL or PFD_DOUBLEBUFFER; nPixelFormat:= ChoosePixelFormat (hdc, @pfd); SetPixelFormat (hdc, nPixelFormat, @pfd); end; //====Начало работы приложения - процедура при создании формы====== procedure TForm1.FormCreate(Sender: TObject); begin SetDCPixelFormat(Canvas.Handle); hrc := wglCreateContext(Canvas.Handle); end; //=================Конецработыприложения======================= procedure TForm1.FormDestroy(Sender: TObject); begin wglDeleteContext(hrc); end; end. Компоненты графической программы В состав графической программы, кроме процедуры рисования, а также традиционных разделов описаний модулей, типов, переменных и пр., входят процедуры настройки графических режимов. Как известно, операционная система Windows средствами графического интерфейса GDI создает так называемый контекст устройства (device context – DC), через который, используя драйверы устройств вывода, осуществляется графический вывод. Контекст устройства является структурой данных стандартного типа HDC, который представляет собой дескриптор (handle) контекста устройства. Контекст устройства определяет комплект графических объектов (кисть, палитру, области отсечения и т.д.) и связанных с ними атрибутов, а также графические режимы, влияющие на вывод. Другими словами, контекст устройства это описание набора графических средств, которыми обладает компьютер. В свою очередь, библиотека OpenGL создает контекст воспроизведения (rendering context – RC), который определяет графические средства, необходимые для выполнения графической программы. Он связывает OpenGL с оконными системами Windows. Обращение к контексту воспроизведения идет через его дескриптор hrc – структуру стандартного типа HGLRC. Таким образом, чтобы начать работать с командами OpenGL, приложение должно создать один или несколько контекстов воспроизведения и сделать текущим один из них. Прежде чем создавать контекст воспроизведения, необходимо установить для него формат пикселей, который определяет свойства поверхности рисования OpenGL и должен совпадать с форматом пикселей соответствующего контекста воспроизведения. Для описания формата пикселей используется специальный тип данных TPixelFormatDescriptor. Это запись со множеством полей, в которых указываются различные настройки графического вывода: глубина каждого основного цвета, наличие двойной буферизации, поддержка оконного вывода, режим отображения цветов, настройки буферов OpenGL и др. Прежде чем установить некоторый желаемый формат пикселей, необходимо направить системе запрос: поддерживает ли она его? Это делается при помощи функции: ChoosePixelFormat(hdc, @pfd):integer; у которой первый параметр hdc – переменная типа HDC – ссылка на контекст устройства, а второй параметр – ссылка на переменную pfd типа TPixelFormatDescriptor. Функция ChoosePixelFormat просматривает в контексте устройства поддерживаемые форматы пикселей и выбирает наиболее близкий к описанному в pfd. Функция возвращает целое число – индекс формата пикселя. Вызов этой функции гарантирует, что OpenGL будет работать с форматом пикселей, поддерживаемым устройством, на которое будет осуществляться вывод изображения. После того как найден формат пикселей, наиболее полно совпадающий с требуемым, можно установить его в контексте отображения. До этого используют функцию:SetPixelFormat (hdc, nPixelFormat, @pfd):boolean; Параметры функции определяют: контекст устройства hdc, для которого устанавливается формат пикселей; целочисленный индекс nPixelFormat, который получен при помощи функции ChoosePixelFormat и определяет конкретный формат пикселей из имеющегося набора форматов; указатель pfd на структуру TPixeIFormatDescriptor. Теперь можно создать контекст воспроизведения OpenGL. Для этого используется функция расширения WGL библиотеки OpenGL: wglCreateContext(hdc):HGLRC. Функция возвращает новый контекст воспроизведения (или NULL - в случае неудачи), который подходит для рисования на устройстве, определенном дескриптором hdc. Контекст воспроизведения (в виде дескриптора) присваивается глобальной переменной hrc. Создавать можно произвольное число контекстов воспроизведения, но для работы с графикой OpenGL необходимо установить единственный текущий контекст воспроизведения. Это делается при помощи функции wglMakeCurrent(hdc, hrc):boolean;. Параметр hdc, как и раньше, определяет контекст устройства, второй параметр hrc (типа HGLRC) определяет контекст воспроизведения OpenGL. Теперь инициализацию OpenGL можно считать завершенной. Перед окончанием работы программы, использующей библиотеку OpenGL, необходимо корректно завершить работу с OpenGL. Сначала надо сделать так, чтобы текущий контекст воспроизведения OpenGL никем не использовался. Для этого достаточно выполнить следующий вызов: wglMakeCurrent(0,0);. Затем необходимо удалить контекст воспроизведения. Для этой цели используется функция wglDeleteContext(hrc):boolean;. Перечисленные действия в заготовке программы оформлены в виде следующих процедур: - пользовательская процедура SetDCPixelFormat задает формат пикселя; - обработчик TForm1.FormCreate создает текущий контекст воспроизведения; - обработчик TForm1.FormDestroy удаляет контекст воспроизведения. Чтобы при выполнении процедуры SetDCPixelFormat сократить время на заполнение полей структуры pfd, эти поля сначала заполняются нулями при помощи процедуры FillChar. Функция ChosePixelFormat автоматически заполняет структуру pfd так, что она соответствует некоторому формату пикселей, который поддерживается видеоплатой компьютера. При необходимости некоторые настройки формата пикселя устанавливаются с помощью флагов. В заготовке для примера установлены: – возможность оконного вывода (PFD_DRAW_TO_WINDOW), – поддержка функций библиотеки OpenGL (PFD_SUPPORT_OPENGL), – возможность двойной буферизации (PFD_DOUBLEBUFFER). Затем сформированный желаемый формат пикселей в обработчике TForm1.FormCreate устанавливается на контекст устройства. Как известно, ссылке на контекст устройства в Delphi соответствует свойство Canvas.Handle формы, поэтому при вызове процедуры SetDCPixelFormat в качестве ссылки hdc используется дескриптор окна формы Form1 – Canvas.Handle. Обработчик TForm1.FormDestroy содержит только функцию удаления контекста воспроизведения. Несколько комментариев к основной рисующей процедуре TForm1.FormPaint. Ее начальный фрагмент wglMakeCurrent(Canvas.Handle, hrc); glMatrixMode(GL_PROJECTION); glLoadIdentity(); glOrtho(-1.0,1.0,-1.0,1.0,-1.0,1.0); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); включает следующие действия. Сначала только что рассмотренной командой расширения WGL устанавливается текущий контекст воспроизведения OpenGL. Затем выполняется установка текущих матриц. Дело в том, что OpenGL выполняет различные преобразования в матричной форме и работает с тремя видами матриц: модельно-видовыми (они описывают геометрические преобразования), проективными (они задают положение координатных систем) и текстурными (они влияют на закон наложения текстуры). Некоторые команды библиотеки, в частности, описанная в подразделе 3.4 команда glLoadIdentity, устанавливают вид различных матриц, поэтому перед выполнением таких команд нужно указывать, к какому виду матриц предполагается их применить. Указывает на это параметр команды glMatrixMode: если это строка GL_MODELVIEW, то команды применяются к модельно-видовым матрицам, если GL_PROJECTION, – к проективным, если GL_TEXTURE, – к текстурным. В приведенном фрагменте команда glLoadIdentity сначала применяется к матрице проецирования (устанавливает ее в исходное состояние), а затем – к матрице аффинных геометрических преобразований. Уже известная команда glOrtho задает положение системы координат и объема видимости сцены. Перечисленные команды относятся к настройкам графического вывода и, как правило, применяются во всех графических программах. Далее в заготовке программы идут команды, назначение которых поясняется в соответствующих разделах учебного пособия. При необходимости они могут быть изменены или удалены. ПРИЛОЖЕНИЕ Б. Задания по геометрическому моделированию и отображению двухмерных объектов Задание 1. Система координат и примитивы OpenGL Цель выполнения задания: изучить на практике отображение простых геометрических фигур в пределах нормализованного объема видимости. Изучаемые команды Команды инициализации: auxInitWindowPosition, auxInitWindowSize, glutInitWindowPosition, glutInitWindowSize. Команды настройки цветов фона и изображения: glClearColor, glClear(GL_COLOR_BUFFER_BIT), glColor. Команды рисования геометрических примитивов: glVertex, glBegin – glEnd. Команды задания стиля вычерчивания: glLineWidth, glEnable(GL_LINE_SMOOTH), glEnable(GL_POINT_SMOOTH). Команда задания стиля (модели) заливки примитивов: glShadeModel(GL_FLAT); . Варианты заданий приведены в таблице Б2.1. Таблица Б2.1
Программа выполнения задания Спроектировать изображение, выбрав координаты вершин, которые ограничивают примитивы. Координаты х и у вершин не должны превышать ±1, координата z берется равной нулю. Выбрать размеры окна вывода. Определить цвет фона (не черный) и цвет изображения – разный для каждого фрагмента изображения. В программу-заготовку добавить команды задания окна и рисования изображения. Использовать формат команды задания вершин glVertex3f. Получить изображение заданных фигур на экране. Изменяя координаты х и у вершин в диапазоне (-5,+5), определить границы объема видимости по соответствующим координатам, а также направления координатных осей и точку их начала. Задать координату z одной из вершин равной +0.5, затем -0.5. Объяснить наблюдаемый эффект. Задать координату z одной из вершин равной +5, затем -5. Объяснить наблюдаемый эффект. Задание 2. Расстановка объектов в сцене Цель выполнения задания: практическое изучение средств, необходимых для выполнения сценарных преобразований. Изучаемые команды Команды задания геометрических преобразований объектов: glLoadIdentity, glTranslate, glRotate, glScale. Команды работы с дисплейным списком: glNewList, glEndList, glCallList. Команды работы со стеком: glPushMatrix, glPopMatrix. Команды работы с буфером глубины: glEnable(GL_DEPHT_TEST), glClear(GL_DEPTH_BUFFER_BIT). Варианты задания приведены в таблице Б2.2. В ней точками показано требуемое расположение трех объектов в поле вывода. В графе «Поворот объектов» заданы углы поворота этих объектов в плоскости экрана. Если объектов больше трех, остальные расставляются по усмотрению студента. Таблица Б2.2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












