Учебная лабораторная установка по курсу теория электрической связи Краткое описание лабораторного стенда
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
Содержание отчета 1. Принципиальная схема исследования. 2. Сток-затворная характеристика исследованной нелинейной цепи. 3. Аппроксимация ВАХ для работы на квадратичном (параболическом), кусочно-линейном и кусочно-параболическом участках. 4. Теоретический расчет спектра для данных, использованных в эксперименте (по указанию преподавателя). 5. Осциллограммы и спектры исследованных процессов. Контрольные вопросы: 1. Каковы характерные особенности спектров тока, протекающего через нелинейный безинерционный элемент, при моно- и бигармоническом воздействиях? 2. Что называется порядком комбинационного колебания? Поясните примером. 3. Какова связь между наивысшим порядком комбинационного колебания и степенью полинома, аппроксимирующего характеристику нелинейного элемента? 4. Перечислите наиболее часто применяемые методы спектрального анализа колебаний на выходе без инерционных нелинейных преобразователей. Укажите, при каких видах аппроксимации целесообразно применять каждый из них. 5. Что называется углом отсечки, как определить его по осциллограмме сигнала и как выразить аналитически? 6. Характеристика нелинейного элемента аппроксимирована ломаной линией. Входное воздействие представляет собой сигнал вида u=ЕСМ+Umcos2t. Пользуясь системой трех координатных плоскостей, покажите, как следует выбрать ЕСМ и Um, чтобы: а) ток по форме повторял форму входного сигнала; б) ток принял форму косинусоидальных импульсов с углом отсечки 900. 7. Поясните, как работает преобразователь, принципиальная схема которого приведена на рисунке 3.4. 8. Как практически изменить положение рабочей точки на сток-затворной характеристике полевого транзистора? 9. Перечислите все составляющие спектра тока, если на вход нелинейного элемента с параболической (квадратичной) ВАХ подать гармонические сигналы с частотами 5 и 6 КГц. 10. То же для случая аппроксимации ВАХ степенным полиномом третьей степени. 11. Как изменится спектральный состав тока, если амплитуду входного напряжения уменьшить в 10 раз? ЛАБОРАТОРНАЯ РАБОТА №4 "ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ ВО ВРЕМЕНИ (ТЕОРЕМА КОТЕЛЬНИКОВА)" Цель работы: исследование процессов дискретизации и восстановления непрерывных сигналов. Краткие сведения из теории Некоторые из непрерывных сигналов имеют ограниченный спектр. Для таких сигналов справедлива теорема Котельникова: непрерывный сигнал с ограниченным спектром полностью определяется своими значениями в дискретные моменты времени, отстоящими друг от друга на время 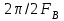 , где Fв – верхняя граничная частота спектра этого сигнала, , где Fв – верхняя граничная частота спектра этого сигнала,  t – называется интервалом дискретизации по времени. t – называется интервалом дискретизации по времени.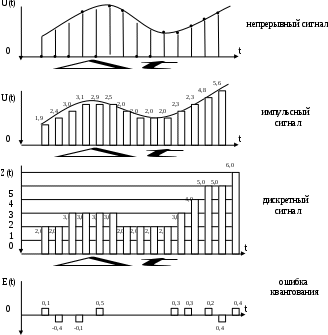 Рисунок 4.1 Дискретизация сигнала На основе теоремы Котельникова непрерывный сигнал с ограниченным спектром может быть передан путем передачи его мгновенных значений, отсчитываемых в дискретные моменты времени – дискретных отсчетов, т. е. фактически задача сводится к передаче последовательности чисел. Эта теорема указывает следующие условия: а) спектр передаваемого сигнала должен быть ограничен верхней граничной частотой Fв; б) частота следствия импульсов – отсчетов или частота дискретизации Fg. Fg 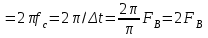 (4.1) (4.1) Если истинное мгновенное значение сигнала U(t), подлежащее передаче попадает между разрешенными значениями, то амплитуда передаваемого импульса принимается равной разрешенному значению, являющемуся ближайшим, к истинному. Такое преобразование называется квантованием, совокупность разрешенных значений амплитуд передаваемых импульсов – шкалой квантования, а интервал между соседними разрешенными значениями – шагом квантования. Квантование приводит к ошибке квантования (шум квантования) E(t)=Z(t) – v(t). Квантование при передаче сигналов, во–первых позволяет применить импульсно – кодовую модуляцию и, следовательно, использовать все преимущества, обеспечиваемые ею, во – вторых представляет собой мощное средство борьбы со случайными помехами. Применяемая аппаратура Исследуемое устройство (рисунок 4.2) размещено на сменном блоке ТЕОРЕМА КОТЕЛЬНИКОВА и представляет собой дискретизатор (обозначенный на макете как перемножитель сигналов) и набор из трех фильтров - восстановителей с разными частотами среза. Источники исследуемых сигналов - S1, S2 и S3 находятся в блоке ИСТОЧНИКИ СИГНАЛОВ, а сами сигналы представляют собой суммы гармоник с частотами 2, 4 и 6кГц. (При необходимости исследуемый сигнал может быть усложнен добавлением еще одного гармонического сигнала с частотой 1кГц с помощью сумматора стенда). Д искретизатор, формирующий отсчеты s(kt) непрерывного сигнала s(t), выполняет функцию перемножителя этого сигнала на короткие импульсы напряжения дискретизации (uдискр). В данном случае дискретизатор выполнен по схеме аналогового коммутатора, пропускающего входной сигнал s(t) на выход в течение короткого времени существования импульсов дискретизации. Временной интервал между соседними отсчетами дискретизированного сигнала s(kt) зависит от выбора частоты дискретизации fд: t=1/ fд. (4.2) Эта частота может изменяться дискретно при нажатии кнопки fд, при этом выбранное значение этой частоты индицируется светодиодом (fд=3,6,12,16,24 и 48 кГц). Все упомянутые выше частоты (частоты дискретизации и частоты гармоник исследуемых сигналов) жестко синхронизированы, что упрощает наблюдение процессов на осциллографе. В качестве фильтров - восстановителей используются три активных ФНЧ четвертого порядка с частотами среза 3, 6 и 12 кГц. Для снятия импульсных характеристик фильтров используется генератор коротких импульсов " - функций" (гнезда (t) в блоке ИСТОЧНИКИ СИГНАЛОВ). 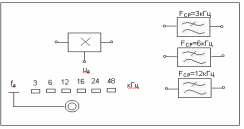 Р исунок 4.2 Сменный блок ТЕОРЕМА КОТЕЛЬНИКОВА В соответствии с теоремой Котельникова отсчеты, следующие через интервалы времени t=1/2FВ, где FВ - верхняя частота сигнала, могут быть преобразованы в исходный сигнал после прохождения через идеальный ФНЧ с частотой среза FСР = FВ. В работе используются реальные ФНЧ с достаточно крутыми спадами АЧХ после частоты среза. Поэтому на практике выбирают t несколько меньше (а иногда и в несколько раз меньше), чем требуется в теореме Котельникова с тем, чтобы реальный ФНЧ с АЧХ трапециевидной формы позволял выделить спектр исходного сигнала из спектра дискретизированного сигнала, что гарантирует отсутствие искажений при обратном преобразовании (восстановлении) сигнала. В качестве измерительных приборов используются двулучевой осциллограф и ПК, работающий в режиме анализатора спектра. Лабораторное задание 1. Произвести дискретизацию одного из сложных сигналов (S1, S2 или S3). 2. Исследовать спектры исходного и дискретизированного сигналов. 3. Исследовать частотные и импульсные характеристики фильтров – восстановителей. 4. Исследовать процесс восстановления дискретизированных сигналов. Порядок выполнения работы Дискретизация сигнала 4.1 Выбрать один из трех сигналов (например, S1) в блоке ИСТОЧНИКИ СИГНАЛОВ и подать его на вход "А" ПК, работающего в режиме спектроанализатора. (Входы ПК находятся в нижней части стенда справа). 4.2 С помощью спектроанализатора (ПК) получить спектр сигнала и определить его верхнюю частоту (FВ). 4.3 Учитывая, что значения частот дискретизации (fд), указанных на сменном блоке, являются ориентировочными, провести спектральный анализ сигналов UД (гнездо под перемножителем). Определив частоты первых гармоник этих сигналов при установке fД = 3, 6, 12 и 16 кГц, внести уточненные значения в таблицу 4.1. Для частот более 24 и 48 кГц спектральный анализ в данной работе невозможен (так как Fmax = 24 кГц), поэтому их следует умножить на тот же коэффициент, который связывает указанные на блоке и уточненные значения частот дискретизации. (Этот коэффициент (≈1,15) может быть уточнен по первым четырем значениям fД). Таблица 4.1 – Уточненные частоты дискретизации (fД)
4.4 Рассчитать требуемую частоту дискретизации fд и установить ее на макете кнопкой " fд ". 4.5 Соединить входы двулучевого осциллографа со входом и выходом дискретизатора, установить режим внешней синхронизации осциллографа (от гнезда С2 блока ИСТОЧНИКИ). Вход спектроанализатора подключить к выходу дискретизатора. 4.6 Зафиксировать в отчете временные диаграммы в следующем порядке (с сохранением масштаба по оси времени) - исследуемый сигнал s(t); - напряжение дискретизации (гнездо нижнего входа перемножителя); - выходной дискретизированный сигнал s(kt). С экрана монитора ПК зарисовать спектры перечисленных выше сигналов. 4.7 Переключая кнопкой частоту дискретизации fд на 1-2 шага выше и ниже выбранного значения fд, наблюдать изменения в осциллограммах и спектрах на выходе дискретизатора. Наиболее характерные случаи зафиксировать в отчете. Исследование фильтров С целью выбора наилучшего из трех ФНЧ в качестве фильтра - восстановителя необходимо определить частоту среза каждого из них по АЧХ либо по импульсной характеристике g(t). Кроме того, АЧХ фильтров необходима для последующей коррекции fд, а импульсная реакция g(t) нужна для объяснения процесса восстановления сигнала. 4.8 Снятие АЧХ фильтра проводиться путем подачи на его вход гармонического сигнала с напряжением 1В и с частотой 1кГц от встроенного генератора Г3-111 в блоке ИСТОЧНИКИ СИГНАЛОВ. К выходу фильтра подключить встроенный цифровой вольтметр переменного напряжения типа В7-38. Плавно увеличивая частоту генератора, снять частотную характеристику UВЫХ=(f) с шагом 1-2кГц так, чтобы зафиксировать частоту среза FС, на которой UВЫХ окажется в2 раз меньше, чем на частоте 1кГц, а также частоты, на которых UВЫХ уменьшится до 0,1 и 0,05 от UВЫХ(1кГц). Построить на одном графике АЧХ трех фильтров и отметить на них уточненные значения частот среза FС. Выбрать лучший фильтр - восстановитель для исследуемого сигнала. 4.9 Снятие импульсной реакции ФНЧ производится путем подачи на вход фильтра коротких импульсов (от гнезда "(t)" блока "ИСТОЧНИКИ"). Осциллограмма выходного сигнала будет соответствовать импульсной реакции фильтра g(t). Зарисовать осциллограммы g(t) для трех фильтров, фиксируя на них значения "нулей" (рисунок 4.3.) по шкале на экране осциллографа с учетом масштаба развертки (мкс/дел). Определив t для каждого ФНЧ, находим частоты среза по формуле: FС =1/(2 t ). (4.3) 4.10 По пунктам (4.8) или (4.9) выбрать фильтр, наиболее пригодный для восстановления дискретизированного сигнала. Р 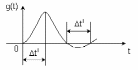 исунок 4.3 Импульсная реакция ФНЧ Восстановление дискретизированного сигнала 4.11 Сопоставляя спектры, снятые по пункту 4.6 с частотной характеристикой выбранного фильтра - восстановителя, скорректировать частоту дискретизации, увеличив ее на 1 - 2 шага от расчетного значения с тем, чтобы спектр исходного сигнала s(t) можно было выделить из спектра дискретизированного сигнала с помощью выбранного реального ФНЧ. 4.12 Соединить выход дискретизатора с входом выбранного ФНЧ, установить на макете уточненное в пункте 4.11 значение fд. Подключив один из входов осциллографа к входу дискретизатора, а второй - к выходу ФНЧ, зафиксировать в отчете осциллограммы исходного и восстановленного сигнала. 4.13 Изменяя частоту дискретизации на 1 - 2 шага от скорректированного значения fд, зафиксировать наиболее характерные осциллограммы восстановленных сигналов. В отчете привести заключение о том, допустимо ли изменять интервал между отсчетами дискретизированного сигнала (t). 4.14 Установив прежнее значение fд, заменить выбранный ФНЧ на другой, а затем и на третий фильтр, фиксируя в отчете осциллограммы восстановленных сигналов с указанием FС ФНЧ. 4.15 Соедините вход дискретизатора с источником периодической последовательности прямоугольных импульсов, в качестве которого используется КОДЕР. Установите тумблерами КОДЕРА любую комбинацию из одной единицы и четырех нулей. При этом на выходе КОДЕРА формируются прямоугольные импульсы длительностью 512мкс с периодом 8704 мкс. Проведя анализ спектра этого сигнала, выберите fд и фильтр восстановитель. Зафиксируйте осциллограммы и спектры входного, дискретизированного и восстановленного сигналов. Содержание отчета 1. Функциональная схема установки. 2. Осциллограммы, спектры и характеристики фильтров по всем пунктам задания. 3. Выводы. Контрольные вопросы: 1. Каков практический смысл в дискретизации аналоговых сигналов? 2. Сформулируйте теорему Котельникова. 3. При каких условиях теорема Котельникова гарантирует двойное преобразование сигналов (дискретизация и восстановление) без искажений? 4. Могут ли быть дискретизированы и затем восстановлены импульсы прямоугольной формы? 5. Каков алгоритм восстановления дискретизированного сигнала? 6. Какова роль ряда Котельникова в объяснении процесса восстановления сигнала? 7. Что такое базисная функция? 8. Какую функцию выполняет ФНЧ? 9. С какой целью в работе исследовались спектры исходного и дискретизированного сигналов? 10. Можно ли произвольно увеличивать или уменьшать t между отсчетами? К чему это может привести? 11. В чем отличие идеального и реального ФНЧ? 12. С чем связана необходимость корректировать значение частоты дискретизации? 13. Как Вы представляете себе процесс дискретизации аналогового сигнала? Какие функциональные узлы для этого необходимы? 14. Все ли аналоговые сигналы могут быть: - дискретизированы во времени; - восстановлены после дискретизации. 15. Назовите причины, вызывающие искажения при восстановлении дискретизированных сигналов. ЛАБОРАТОРНАЯ РАБОТА №5 АМПЛИТУДНАЯ МОДУЛЯЦИЯ Цель работы: исследование процесса амплитудной модуляции, получение статической модуляционной характеристики и выбор оптимального режима работы модулятора. Краткие сведения из теории Для сигналов с аналоговыми видами модуляции удобно использовать квазигармоническое представление: 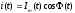 , ,где 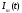 - огибающая процесса, - огибающая процесса,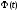 - полная фаза - полная фаза 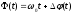 . .Первое слагаемое здесь - текущая фаза, второе - девиация (отклонение) фазы. Учитывая, что 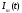 и и 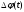 - суть медленно меняющиеся функции времени, за один период колебания с несущей частотой 0, модулированный сигнал по форме представляет собой синусоиду. Этим и объясняется название "квазигармоническое", то есть почти синусоидальной формы. - суть медленно меняющиеся функции времени, за один период колебания с несущей частотой 0, модулированный сигнал по форме представляет собой синусоиду. Этим и объясняется название "квазигармоническое", то есть почти синусоидальной формы.Амплитудную модуляцию можно определить как вид модуляции, при котором девиация амплитуды пропорциональна информационному сигналу 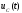 , а девиация фазы , а девиация фазы 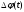 вырождается в начальную фазу вырождается в начальную фазу 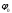 . .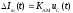 , , 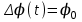 (5.1) (5.1)где КАМ - коэффициент пропорциональности, характеризующий работу модулятора. Физический смысл этого коэффициента будет показан ниже. Огибающая процесса 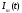 может быть представлена как сумма постоянной составляющей (амплитуды несущего колебания) и девиации амплитуды: может быть представлена как сумма постоянной составляющей (амплитуды несущего колебания) и девиации амплитуды: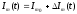 (5.2) (5.2) Общая запись амплитудно-модулированного сигнала (АМ) имеет вид: 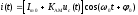 (5.3) (5.3) Для частного случая, тональной АМ: 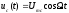 ; ( ; (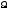 0) 0)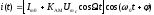 . .Величина 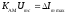 ; вынося ; вынося 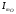 за скобку, получим: за скобку, получим: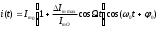 Обозначим 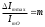 (глубина модуляции). (глубина модуляции).Окончательно для тональной модуляции: 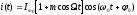 (5.4) (5.4) Для модуляции сложным сигналом 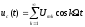 , а , а 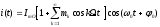 здесь 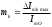 - частичная (парциальная) глубина модуляции; - частичная (парциальная) глубина модуляции;  . .Временные диаграммы информационного сигнала 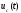 и сигнала АМ представлены на рисунок 6.1. и сигнала АМ представлены на рисунок 6.1.Для получения спектра тонального АМ сигнала раскроем скобки выражения (6.4) 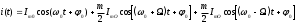 . .С 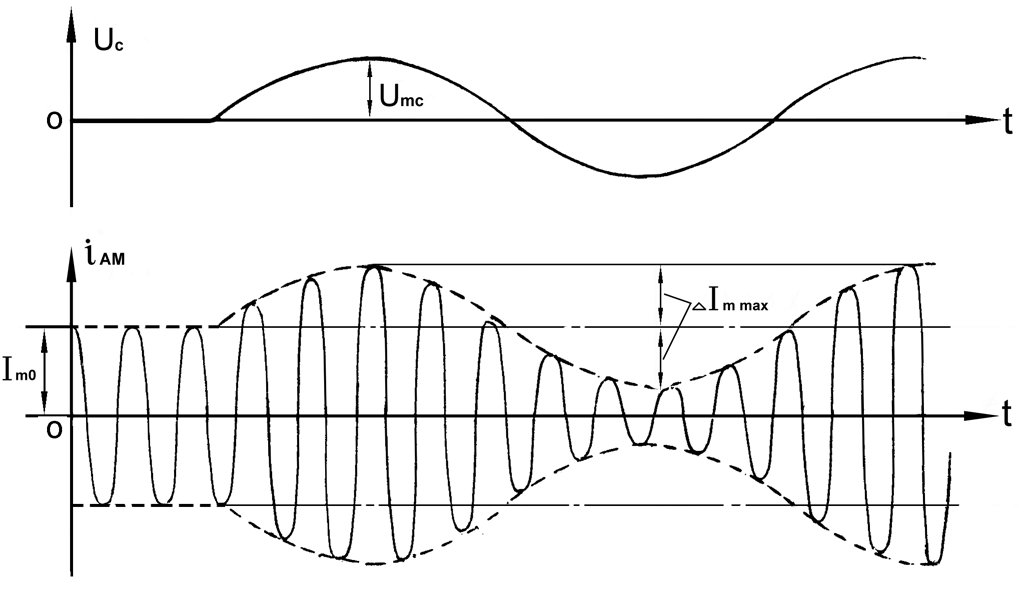 пектрограммы исходного (информационного) сигнала и АМ сигнала показаны на рисунке 5.2. Рисунок 5.1 Временные диаграммы тонального АМ сигнала Спектр тонального АМ сигнала состоит из колебания несущей частоты и двух боковых, которые являются комбинационными частотами. Итак, новыми колебаниями, возникающими в амплитудном модуляторе, являются комбинационные колебания второго порядка 0 . Следовательно, наилучшей формой ВАХ нелинейного элемента в амплитудном модуляторе является квадратичная парабола: 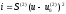 при при 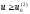 . Если на вход нелинейного элемента подать бигармонический сигнал . Если на вход нелинейного элемента подать бигармонический сигнал 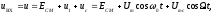 в спектре тока в спектре тока  , кроме гармоник входных сигналов, образуются комбинационные колебания второго порядка , кроме гармоник входных сигналов, образуются комбинационные колебания второго порядка 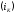 : :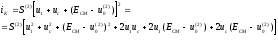 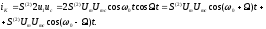 (5.5) (5.5) 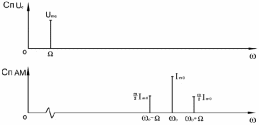 Рисунок 5.2 Спектр тонального АМ сигнала Весь спектр тока  показан на рисунке 6.3 Для выделения из спектра тока полезных компонентов сигнала (0, 0) необходимо применить полосовой фильтр с центральной частотой 0 и полосой пропускания не уже 2. показан на рисунке 6.3 Для выделения из спектра тока полезных компонентов сигнала (0, 0) необходимо применить полосовой фильтр с центральной частотой 0 и полосой пропускания не уже 2. Рисунок 5.3 Спектры амплитудного модулятора В простейшем варианте таким полосовым фильтром может быть параллельный контур с невысокой добротностью. (При высокой добротности контура в спектре выходного напряжения будут подавлены боковые частоты). Для нахождения оптимального режима работы модулятора следует получить (расчетным или экспериментальным путем) статическую модуляционную характеристику (СМХ) 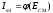 при при 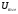 = const. Эта характеристика показывает возможности модулятора в изменении амплитуды сигнала. = const. Эта характеристика показывает возможности модулятора в изменении амплитуды сигнала.Строятся несколько таких характеристик для разных амплитуд колебаний несущей частоты ( 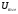 ), и из них выбирается та, которая имеет наибольший по протяженности линейный участок. Требование линейности СМХ вытекает из определения АМ. Тангенс угла наклона линейного участка СМХ (угла на рисунке 5.4) является коэффициентом пропорциональности КАМ. С помощью СМХ можно определить оптимальный режим амплитудного модулятора и его параметры: ), и из них выбирается та, которая имеет наибольший по протяженности линейный участок. Требование линейности СМХ вытекает из определения АМ. Тангенс угла наклона линейного участка СМХ (угла на рисунке 5.4) является коэффициентом пропорциональности КАМ. С помощью СМХ можно определить оптимальный режим амплитудного модулятора и его параметры:- выбор оптимальной амплитуды сигнала несущей частоты 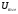 (по максимальной протяженности линейного участка СМХ); (по максимальной протяженности линейного участка СМХ);- границы линейного участка СМХ (средняя точка линейного участка соответствует оптимальному напряжению смещения и амплитуде несущего колебания (по вертикальной оси)); - максимальная амплитуда модулирующего сигнала 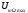 - половина проекции линейного участка СМХ на горизонтальную ось графика; - половина проекции линейного участка СМХ на горизонтальную ось графика;- максимальная девиация амплитуды 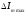 - половина проекции линейного участка СМХ на вертикальную ось; - половина проекции линейного участка СМХ на вертикальную ось;- 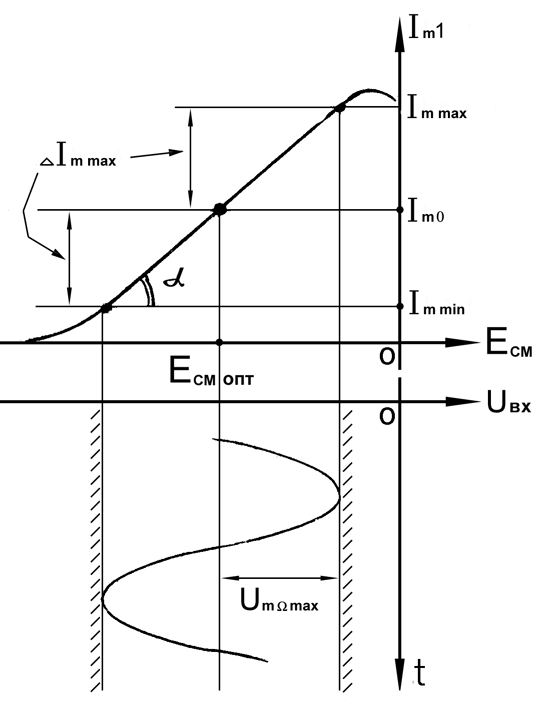 максимально достижимая глубина модуляции 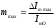 . .Рисунок 5.4 Статическая модуляционная характеристика Разновидности амплитудной модуляции В спектре тональной АМ присутствуют две боковые частоты, являющиеся комбинационными колебаниями второго порядка 0 и несущая 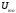 на частоте 0. Информация о модулирующем сигнале на частоте 0. Информация о модулирующем сигнале 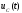 содержится в боковых составляющих спектра, причем их амплитуды пропорциональны амплитуде модулирующего сигнала содержится в боковых составляющих спектра, причем их амплитуды пропорциональны амплитуде модулирующего сигнала 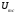 , а расстояние по оси частот от несущей 0 - содержит информацию о частоте модулирующего сигнала . Амплитуда несущего колебания , а расстояние по оси частот от несущей 0 - содержит информацию о частоте модулирующего сигнала . Амплитуда несущего колебания 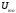 не зависит от модулирующего сигнала и в этом смысле несущее колебание, вопреки своему названию, никакой информации не несет (кроме того факта, что передатчик работает). не зависит от модулирующего сигнала и в этом смысле несущее колебание, вопреки своему названию, никакой информации не несет (кроме того факта, что передатчик работает).Даже при максимальной амплитуде модулирующего сигнала (m=1) амплитуда несущей 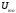 в 2 раза превышает амплитуду каждой из боковых в 2 раза превышает амплитуду каждой из боковых 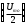 . При малых значениях модулирующего сигнала (m0) это соотношение значительно возрастает. Следовательно, на полезную часть спектра АМ сигнала приходится малая часть мощности передатчика, а подавляющая часть ее расходуется бесполезно - на создание гармонического колебания на частоте 0. Поэтому возникло предложение удалить несущую из спектра АМ сигнала, что дает значительный экономический эффект либо позволит увеличить дальность связи, так как теперь вся мощность передатчика будет расходоваться на создание колебаний боковых частот. Такую разновидность АМ называют балансной (БАМ). Сигнал с балансной АМ можно получить путем перемножения несущей . При малых значениях модулирующего сигнала (m0) это соотношение значительно возрастает. Следовательно, на полезную часть спектра АМ сигнала приходится малая часть мощности передатчика, а подавляющая часть ее расходуется бесполезно - на создание гармонического колебания на частоте 0. Поэтому возникло предложение удалить несущую из спектра АМ сигнала, что дает значительный экономический эффект либо позволит увеличить дальность связи, так как теперь вся мощность передатчика будет расходоваться на создание колебаний боковых частот. Такую разновидность АМ называют балансной (БАМ). Сигнал с балансной АМ можно получить путем перемножения несущей 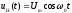 и модулирующего сигнала и модулирующего сигнала 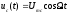 . На выходе перемножителя получим: . На выходе перемножителя получим: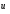 вых= вых=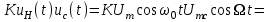 = 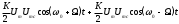 =uБМ(t). (5.6) =uБМ(t). (5.6)При этом никаких фильтров не требуется. Такую операцию можно выполнить на аналоговых перемножителях сигналов или на симметричных (балансных) схемах, которые и дали название этой разновидности АМ. Дальнейшим "усовершенствованием" БМ является отказ от одной из боковых полос (для тональной модуляции - одной из боковых составляющих), так как каждая из них содержит одинаковую информацию о модулирующем сигнале. Так возникла еще одна разновидность АМ - однополосная модуляция (ОБП - одна боковая полоса или SSB - Single Side Band). Судя по спектру сигнала с ОБП, последний может быть получен путем переноса спектра модулирующего низкочастотного сигнала вверх по оси частот на частоту 0 (подобно процессу преобразования частоты). Существенным достоинством ОБП по сравнению с БМ является вдвое меньшая полоса, занимаемая спектром сигнала, а общим недостатком БМ и ОБМ являются трудности при детектировании этих сигналов, вызванные отсутствием несущей. Существует еще одна разновидность АМ - полярная модуляция (ПМ). Дело в том, что верхняя и нижняя огибающие обычного АМ сигнала симметричны относительно оси времени (следовательно, несут одинаковую информацию о модулирующем сигнале) а при детектировании обычно используется только одна из огибающих. Возникла идея использовать другую огибающую для передачи второго модулирующего сигнала на одной несущей. Практически эта идея реализована в отечественной системе стереофонического вещания в УКВ диапазоне. Рассмотрим простейший случай, когда по двум каналам передаются гармонические сигналы разных частот: 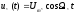 , , 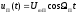 Сигнал с полярной модуляцией: 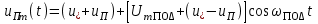 , (5.7) , (5.7) где 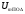 и и 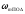 - соответственно, амплитуда и частота так называемого поднесущего колебания; индексы "" и "п" относятся к левому и правому каналам. Таким образом, ПМ сигнал состоит из суммарного низкочастотного сигнала - соответственно, амплитуда и частота так называемого поднесущего колебания; индексы "" и "п" относятся к левому и правому каналам. Таким образом, ПМ сигнал состоит из суммарного низкочастотного сигнала 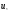 + +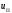 (монофонический сигнал, не содержащий информации о пространственном расположении источников звука) и сигнала поднесущей частоты, промодулированного по амплитуде разностным сигналом ( (монофонический сигнал, не содержащий информации о пространственном расположении источников звука) и сигнала поднесущей частоты, промодулированного по амплитуде разностным сигналом (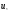 - -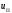 ), в котором содержится информация о пространственном расположении источников звука. Определим огибающие ПМ сигнала: ), в котором содержится информация о пространственном расположении источников звука. Определим огибающие ПМ сигнала:- верхняя огибающая 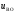 (при (при 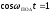 ): ):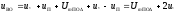 ; ;- нижняя огибающая 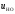 (при (при 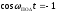 ): ):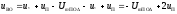 . .Отсюда видно, что верхняя огибающая содержит информацию о сигналах только левого канала, а нижняя - только правого канала. Здесь надо отметить, что ПМ сигнал не является модулированным (в точном значении этого понятия), так в его спектре кроме модулированного по амплитуде сигнала поднесущей есть ещё и исходный низкочастотный сигнал ( 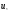 + +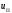 ). Напомним, что модулированные сигналы являются высокочастотными, то есть для них выполняется условие: ). Напомним, что модулированные сигналы являются высокочастотными, то есть для них выполняется условие: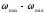 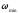 (5.8) (5.8) Для большей наглядности приведем спектр рассматриваемого ПМ сигнала (рисунок 6.5), из которого видно, что условие (6.7.) для этого сигнала не выполняется. Поэтому для передачи ПМ сигнала по радиоканалу необходима дополнительная модуляция (обычно ЧМ) на более высокой несущей частоте 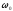 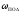 . .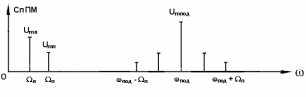 Рисунок 5.5 Спектр простейшего полярно-модулированного сигнала |
