Учебная лабораторная установка по курсу теория электрической связи Краткое описание лабораторного стенда
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
Порядок выполнения работыМоногармонический сигнал 2.1 Подключить осциллограф к гнезду “1 кГц” стенда. Ручку регулятора выхода сигнала поставить в среднее положение. Зафиксировать в отчёте осциллограмму сигнала и измерить его период по делениям на экране с учётом цены деления (мкс/дел) переключателя развёртки. 2.2 Соединить гнездо “1кГц” с входом ПК, расположенным в нижней части стенда, правее сменного блока. Для этого надо применять специальный кабель (входит в комплект стенда) с разъёмом типа “колокольчик”. Процедура анализа спектра с помощью ПК описана в Приложении. Зафиксируйте в отчёте спектр сигнала, указав там условия эксперимента, амплитуды и точные значения частот спектральных линий (в обозначениях на стенде даны округлённые значения частот). Сложные гармонические сигналы 2.3 Подавая сигнал от гнезда S1 блока ИСТОЧНИКИ СИГНАЛОВ на вход осциллографа, зафиксировать форму S1(t) исследуемого сигнала и его период, а затем – на вход ПК, фиксируя амплитуды и частоты спектра сигнала. 2.4 Повторить п. 2.3 для сигналов S2 и S3. 2.5 Подать сигнал S2 на один из входов сумматора () стенда; на второй его вход – сигнал от гнезда “1кГц”. Наблюдая осциллограмму сигнала на выходе сумматора, плавно увеличивать уровень сигнала “1кГц”, добиваясь заметного изменения формы суммарного сигнала. Для полученного суммарного сигнала зафиксировать осциллограмму (с указанием периода) и его спектр. Бигармонический сигнал 2.6 Бигармонический сигнал состоит из двух гармонических сигналов, частоты которых не обязательно находятся в кратных соотношениях. Такими сигналами в данном случае будут: вышеупомянутый “1кГц” из блока ИСТОЧНИКИ СИГНАЛОВ и 1,2 кГц от встроенного ЗГ типа Г3-111. Оба этих сигнала надо подать на входы сумматора, выставив напряжение каждого из них по 0,5 В. Для этого использовать встроенный вольтметр В7-38. Подать суммарный сигнал сначала на осциллограф, зафиксировать его форму с указанием периода суммарного сигнала, а затем на вход ПК, зафиксировав его спектр. Периодическая последовательность прямоугольных импульсов 2.7 Периодическая последовательность прямоугольных импульсов формируется в блоке КОДЕР. “Нули” и ”единицы” цифрового сигнала задаются пятью тумблерами (b1b5) со светодиодной индикацией с надписью ПЕРЕДАНО. 2.8 Соединить выходные гнёзда КОДЕРА с входом осциллографа и ПК. 2.9 Набрать в КОДЕРЕ комбинацию 10000 (длительность импульса Т=512 мкс, а период – 17Т). Зафиксировать в отчёте форму и спектр сигнала. 2.10 Повторить п.2.9, набрав комбинацию 11000 (длительность импульса 2Т=1024мкс, период – 17Т). 2.11 Повторить п. 2.9 для комбинации 11110 (длительность импульса 4Т=2048мкс, период – 17Т). Содержание отчета1. Название сигнала, осциллограмма с указанием периода сигнала, спектрограмма с указанием амплитуд в делениях и частот составляющих в Герцах; 2. Выводы. Контрольные вопросы:1. Какова математическая связь формы периодического сигнала и его спектра? 2. То же для непериодических (однократных) сигналов. 3. Что такое прямое и обратное преобразование Фурье? 4. В каких случаях можно применить ряд Фурье для спектрального анализа? 5. Меняется ли спектр сложного сигнала при прохождении его через линейную цепь (например, ФНЧ)? 6. Меняется ли форма моногармонического сигнала при прохождении его через ФВЧ? 7. Меняется ли форма сложного сигнала при прохождении его через линейный четырёхполюсник? 8. Что такое спектральная плотность амплитуд? 9. Влияет ли фазовый спектр сигнала на его форму? 10. От каких параметров сигнала зависит спектр периодической последовательности прямоугольных импульсов? 11. Как связана длительность сигнала и ширина его спектра? ЛАБОРАТОРНАЯ РАБОТА №3 "ПРЕОБРАЗОВАНИЕ ФОРМЫ И СПЕКТРА СИГНАЛОВ БЕЗИНЕРЦИОННЫМ НЕЛИНЕЙНЫМ ЭЛЕМЕНТОМ " Цель работы: изучение формы и спектра сигналов на выходе резистивной цепи, содержащей нелинейный безинерционный элемент при моно- и бигармоническом воздействии. Краткие сведения из теории Исследование нелинейной цепи задача весьма сложная в том отношении, что при математическом описании функционирования такой системы мы сталкиваемся с проблемой решения нелинейных дифференциальных уравнений. Известно, что здесь не применимы большинство приёмов и методов, которые позволяют относительно легко решать линейные дифференциальные уравнения с постоянными коэффициентами. Тем не менее, в ряде случаев исследования нелинейных систем удаётся довести до конца простыми способами. Для этого достаточно потребовать, чтобы нелинейная зависимость вида: Uвых(t)=f(Uвх,t) (3.1) Не содержала явно времени. Физически такое требование означает безинерционность нелинейного элемента, т.е. мгновенное установление выходной реакции вслед за изменением внешнего входного воздействия. Безинерционных нелинейных элементов, строго говоря, не существуют. Однако эта идеализация достаточно точна, если характерное время изменения входного сигнала значительно превышает время установления процесса внутри самого нелинейного элемента. В радиотехнике нелинейные элементы – это чаще всего полупроводниковые приборы – диоды, биполярные и полевые транзисторы. Современные полупроводниковые приборы достаточно совершенны по своим частотным свойствам. Поэтому предположение о безинерционном характере внутренних процессов в нелинейных радиотехнических элементах часто бывает оправданным. Функциональную зависимость, рассмотренную ранее можно представить как простейшую математическую модель нелинейного элемента. Особенность её состоит в том, что здесь не фигурируют процессы, происходящие внутри элемента. Принято говорить, что имеют дело с внешней характеристикой системы. Можно выделить класс элементов с однозначными вольтамперными характеристиками и класс элементов, характеристики которых содержат участки многозначности. Классификация цепей Радиотехнические цепи и элементы, используемые для осуществления преобразовании сигналов и колебаний (преобразование исходного сообщения в электрический сигнал и кодирование, генерация высокочастотных колебаний, управление колебаниями (модуляция), выделение сообщения из высокочастотного колебания (детектирование о декодирование)) можно разбить на следующие классы: - линейные цепи с постоянными параметрами, - линейные цепи с переменными параметрами, - нелинейные цепи. В реальных радиоустройствах четкое выделение линейных и нелинейных цепей и элементов не всегда возможно. Отнесение одних и тех же элементов к линейным или нелинейным часто зависит от уровня воздействующих на них сигналов. Радиотехническое устройство независимо от своего назначения и уровня сложности представляет собой систему, т.е. совокупность физических объектов, между которыми существуют определенные взаимодействия.  Рисунок 3.1 - Система (системный оператор) На вход подается исходный сигнал, а с выхода снимается преобразованный сигнал. Система представляет <<черный ящик>>, если интересуются лишь связью между сигналами на входе и выходе и не описывают внутренние процессы в системе. Сигнал Uвых - результат воздействия системного оператора Т на сигнал Uвх. Uвых=Т Uвх (3.2) Линейные цепи с постоянными параметрами 1. Цепь является линейной, если входящие в нее элементы не зависят от внешней силы (напряжения, тока), действующей на цепь. 2. Линейная цепь подчиняется принципу суперпозиции (наложения). 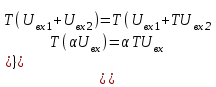 (3.3) (3.3)где 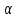 - произвольное число. - произвольное число.Суть принципа суперпозиции: при действии на линейную цепь нескольких внешних сил поведение цепи (ток, напряжение) можно определить путем наложения (суперпозиции) решений, найденных для каждой из сил в отдельности. 3. При сколь угодно сложном воздействий в линейной цепи с постоянными параметрами не возникает колебаний новых частот. Ни одно из преобразований сигналов, сопровождающихся появлением новых частот (т.е. частот, отсутствующих в спектре входного сигнала) не может в принципе быть осуществлено с помощью линейной цепи с постоянными параметрами. Это вытекает из того факта, что при гармоническом воздействии на линейную цепь с постоянными параметрами колебания на выходе также остается гармоническим с той же частотой, что и на входе, изменяются лишь амплитуда и фаза колебания. Такие цепи находят широчайшее применение для решения задач, не связанных с трансформацией спектра, таких как линейное усиление сигналов, фильтрация (по частотному признаку) и т.д. Линейные цепи с переменными параметрами Одно или несколько параметров изменяются во времени (но не зависят от сигнала). Подобные цепи часто называются линейными параметрическими, свойства 1 и 2 (для линейных цепей с постоянными параметрами) справедливы и для линейных параметрических цепей. Однако, в отличие от предыдущего случая, даже простейшее гармоническое воздействие создает в линейной цепи с переменными параметрами сложное колебание, имеющие спектр частот. Линейная цепь с переменными параметрами преобразует частотный спектр воздействия и, следовательно, может быть использовано для некоторых преобразований сигналов, сопровождающихся трансформацией спектра. Нелинейные цепи Если условие (3.3) не выполняется, то говорят, что система является нелинейной. Радиотехническая цепь является нелинейной, если в ее состав входят один или несколько элементов, параметры которых зависят от уровня входного сигнала. Все физические системы, с которыми имеет дело радиотехника, в той или иной степени нелинейные. Нелинейные радиотехнические устройства содержать в себе обычно такие элементы, как полупроводниковые диоды и транзисторы, имеющие ВАХ сложного вида. 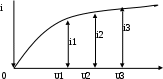 Рисунок 3.2 Вольт–амперная характеристика нелинейного элемента (диода) Основные свойства нелинейных систем: 1. К нелинейным цепям принцип суперпозиции неприемлем. Это свойство нелинейных цепей тесно связано с кривизной вольт – амперных (или иных аналогичных) характеристик нелинейных элементов, нарушающей пропорциональность между током и напряжением. Например, для диода если напряжению U, соответствует ток i1, а напряжению U2 – ток i2, то суммарному напряжению U3= U1+ U2 будет соответствовать току i3 отличный от суммы i1+ i2. При анализе воздействия сложного сигнала на линейную цепь его нельзя разлагать на более простые, необходимо искать облик цепи на результирующий сигнал. Достоинством линейной цепи является, то что, по крайней мере, теоретически можно решить любую задачу о преобразовании входного сигнала такой системы. Недостаток линейной цепи - сложность. Далеко не все результаты могут быть получены аналитическим путем. Непременность для нелинейных цепей принципа суперпозиции делает непригодными спектральных и иные методы анализа, основные на разложении сложного сигнала на составляющие. Однако именно с помощью нелинейных элементов осуществляются важнейшие преобразования радиотехнических синапов. 2. Важным свойством нелинейной цепи является преобразование спектра сигнала. При воздействии на нелинейную цепь простейшего гармонического сигнала в цепи помимо колебаний основной частоты возникают гармоники с частотами, кратными основной частоте. При сложной форме сигнала в нелинейной цепи помимо гармоник возникают еще и колебания с комбинационными частотами, являющиеся результатами взаимодействия отдельных колебаний, входящих в состав сигнала.  Рисунок 3.3 Спектр сигнала Краткая характеристика исследуемых цепей и сигналов В данной работе используется универсальный лабораторный стенд со сменным блоком НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ. Принципиальная схема исследуемой цепи (рис. 3.1) содержит резистивный усилительный каскад на полевом транзисторе. Для формирования этой схемы достаточно переключатель НАГРУЗКА (RVLC) установить в положение "R"; состояние остальных переключателей макета безразлично (колебательный контур и связанные с ним цепи в данной работе не используются). ЕСМ  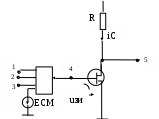 Рисунок 3.4 Принципиальная схема исследуемой цепи Источниками входных сигналов служат внутренние генераторы, гнезда, и регуляторы выходного напряжения которых расположены в левой части стенда (в блоке ИСТОЧНИКИ СИГНАЛОВ). Там же находится встроенный звуковой генератор типа Г3-111. Входные сигналы, подаваемые на любые из трех входов макета (гнезда 13), а также напряжение смещения ЕСМ, через сумматор () подаются на затвор полевого транзистора (гнездо 4). Сумматор выполнен на операционном усилителе; его коэффициент передачи по каждому входу равен единице. Схема сумматора исключает взаимное влияние между входами 1,2 и 3, что позволяет измерять напряжения каждого источника, непосредственно на входе сумматора, не отключая остальные источники. Выходом макета является гнездо 5 в цепи стока. Напряжение смещения устанавливается движковым потенциометром в правой части стенда (ручкой ЕСМ) и контролируется вольтметром, расположенным выше. Для измерения постоянной составляющей тока стока (iС) там же расположен микроамперметр. Для включения прибора в цепь стока следует нажать кнопку "iС" в середине сменного блока. В работе используются также встроенный вольтметр переменного напряжения типа В7-38, двулучевой осциллограф и персональный компьютер (ПК), который в данной работе используется в качестве спектроанализатора. Лабораторное задание 1. Снимите и постройте вольт-амперную характеристику нелинейного элемента. 2. Исследуйте преобразование формы и спектра моногармонического сигнала на квадратичном участке вольт-амперной характеристики нелинейного элемента. 3. Исследуйте преобразование формы и спектра бигармонического сигнала на квадратичном участке вольт-амперной характеристики нелинейного элемента. Порядок выполнения работы 3.1 Снятие вольтамперной (сток-затворной) характеристики полевого транзистора iС=f(ЕСМ) производится путем последовательной установки ряда напряжений смещения (таблица 3.1), измеряя для каждого из них значения тока стока iС. Для последнего необходимо нажать кнопку " iС ", не имеющую фиксации, и снять отсчет со встроенного миллиамперметра. Таблица 3.1
При этом следует учесть, что полное отклонение стрелки этого прибора - 5,0 мА, и не зависит от положения переключателя пределов измерений. Во избежание ошибок при снятии вольтамперной характеристики следует отключать все провода от входов сумматора. После заполнения таблицы построить график iС(ЕСМ). iC   Моногармоническое воздействие 3.2 Моногармоническое воздействие uЗИ = ЕСМ + Umcos2f1t. На построенной вольт-амперной характеристике (ВАХ) определить границы квадратичного участка (u0ЕСМ 0). Преобразование на квадратичном участке ВАХ 3.3 Положение рабочей точки выбирается на середине квадратичного участка ВАХ, т.е. ЕСМ1 = u0/2, где u0 - напряжение отсечки (рисунок 3.6.). Установить полученное значение ЕСМ1 потенциометром ЕСМ и занести его в таблицу 3.2. iC  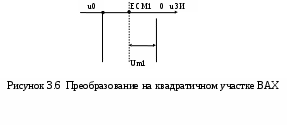 Таблица 3.2
3.4 Амплитуда входного сигнала Um1 должна быть такой, чтобы сигнал занимал весь квадратичный участок ВАХ (от нуля до отсечки), т.е. Um1=ЕСМ1 (рисунок 3.6). Ввиду того, что измерительные приборы имеют градуировку в действующих (U), а не амплитудных (Um) значениях, следует установить на входе макета (гнезда 1, 2 или 3) такое напряжение от источника "1кГц" (левое верхнее гнездо стенда), чтобы подключенный к входу вольтметр показывал: U1= Um1 /2. (3.4) 3.5 Временные диаграммы и спектры при моногармоническом сигнале наблюдается на входе (гнездо 4) и выходе (гнездо 5) преобразователя. Они зарисовываются друг под другом с сохранением соответствия, как по оси времени, так и по оси частот. Для анализа спектра на ПК соответствующее гнездо стенда соединить специальным проводом с входом "А" ПК, расположенным внизу стенда, левее встроенного вольтметра В7-38. На приводимых спектрограммах обязательно указывать частоты в Гц и амплитуды спектральных составляющих. Эти же данные внести в таблицу 3.2. Преобразование на кусочно-параболическом участке ВАХ 3.6 Установить ЕСМ2 = u0. 3.7 Установить амплитуду входного сигнала Um2=u0 (рисунок 3.7). Обратите внимание на используемое здесь обозначение: Um2 означает второе значение амплитуды входного сигнала (не путать со второй гармоникой). 3.8 Повторить пункт 3.5 для ЕСМ2 и Um2, заполнив таблицу 3.3, подобную таблице 3.2. Um2 iC   0 uЗИ u0  ЕCМ2    Um2   Рисунок 3.7 Преобразование на кусочно-параболическом участке ВАХ Бигармоническое воздействие 3.9 Бигармоническое воздействие uЗИ = ЕСМ + U1mcos2f1t+ U2mcos2f2t В качестве второго гармонического сигнала с частотой f2=1,2кГц используется звуковой генератор Г3-111 в блоке ИСТОЧНИКИ. На один из входов сумматора подать прежний сигнал f1=1кГц, на любой другой - f2=1,2кГц. Преобразование на квадратичном участке ВАХ 3.10. Установить смещение ЕСМ=ЕСМ1=u0/2 (рабочая точка на середине квадратичного участка ВАХ). 3.11 Установить одинаковые амплитуды сигналов от разных источников на обоих входах сумматора U1m=U2m=u0/4, при этом суммарный сигнал ("биения") не выйдет за пределы квадратичного участка. 3.12 Повторить п.3.5 для новых параметров сигналов, заполнив соответствующую таблицу. 3.13 Повторить п. 3.5., предварительно уменьшив вдвое амплитуду одного из сигналов. Преобразование на кусочно-параболическом участке ВАХ 3.14 Установить ЕСМ=ЕСМ2=u0 3.15 Установить амплитуды сигналов U1m=U2m= u0/2 3.16 Повторить п. 3.5 для новых параметров сигналов. |
