Номер урока/
занятия
|
Содержание (разделы, темы)
|
Коли-чество часов
|
Даты проведения
|
Материально-техническое оснащение
|
Универсальные учебные действия (УУД), проекты, ИКТ-компетенции, межпредметные понятия
|
план
|
факт
|
I.Геометрические фигуры
|
13
|
|
|
|
|
|
Многоугольники
|
13
|
|
|
ММС
|
Объяснять, что такое:
— четырёхугольник и его элементы (вершины, стороны (противолежащие и соседние), диагонали);
— параллелограмм, прямоугольник, ромб, квадрат;
— средняя линия треугольника;
— трапеция и её элементы, средняя линия трапеции, равнобокая трапеция. Формулировать и доказывать теоремы:
— признак параллелограмма;
— свойство диагоналей параллелограмма;
— свойство противолежащих сторон и углов параллелограмма;
— свойства диагоналей прямоугольника и ромба;
— Фалеса;
— свойства средних линий треугольника и трапеции;
— о пропорциональных отрезках.
Понимать, что квадрат есть одновременно и прямоугольник, и ромб.
|
1
|
Четырёхугольники.
|
1
|
02.09
|
|
2
|
Параллелограмм. Свойства и признаки параллелограмма.
|
1
|
07.09
|
|
3
|
Параллелограмм. Свойства и признаки параллелограмма.
|
1
|
09.09
|
|
4
|
Ромб. Свойства и признаки ромба.
|
1
|
14.09
|
|
5
|
Прямоугольник. Свойства и признаки прямоугольника.
|
1
|
16.09
|
|
6
|
Прямоугольник. Свойства и признаки прямоугольника.
|
1
|
21.09
|
|
7
|
Квадрат. Свойства и признаки квадрата
|
1
|
23.09
|
|
8
|
Контрольная работа № 1 по теме «Параллелограмм. Прямоугольник. Ромб. Квадрат»
|
1
|
28.09
|
|
9
|
Трапеция
|
1
|
30.09
|
|
10
|
Трапеция
|
1
|
05.10
|
|
11
|
Равнобедренная трапеция.
|
1
|
07.10
|
|
12
|
Равнобедренная трапеция.
|
1
|
12.10
|
|
13
|
Контрольная работа № 2 по теме «Трапеция»
|
1
|
14.10
|
|
II. Отношения
|
6
|
|
|
|
Строить с помощью циркуля и линейки четвёртый пропорциональный отрезок.
Решать задачи на вычисление, доказательство и построение, используя изученные признаки, свойства и теоремы
|
|
Параллельность прямых
|
3
|
|
|
|
14
|
Теорема Фалеса.
|
1
|
19.10
|
|
15
|
Теорема Фалеса.
|
1
|
21.10
|
|
16
|
Теорема Фалеса.
|
1
|
26.10
|
|
|
Подобие
|
3
|
|
|
17
|
Пропорциональные отрезки
|
1
|
28.10
|
|
18
|
Пропорциональные отрезки
|
1
|
09.11
|
|
19
|
Пропорциональные отрезки
|
1
|
11.11
|
|
III. Измерения и вычисления
|
14
|
|
|
|
|
|
Измерения и вычисления
|
14
|
|
|
|
|
20
|
Инструменты для измерений и построений; измерение и вычисление углов, длин (расстояний), площадей.
|
1
|
16.11
|
|
ММС
|
Объяснять, что такое:
— косинус, синус, тангенс и котангенс острого угла прямоугольного треугольника;
— перпендикуляр, наклонная, её основание и проекция;
— египетский треугольник. Формулировать и доказывать:
— теорему Пифагора;
— теорему о зависимости косинуса от градусной меры угла;
— неравенство треугольника;
— тождества 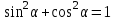 , ,
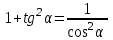 , ,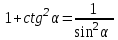 , ,
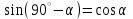 , ,
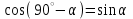 . .
Понимать, что:
— любой катет меньше гипотенузы;
— косинус любого острого угла меньше 1;
— наклонная больше перпендикуляра;
— равные наклонные имеют равные проекции, а больше та, у которой проекция больше;
— любая сторона треугольника меньше суммы двух других;
— синус и тангенс зависят только от величины угла
Знать:
— как выражаются катеты и гипотенуза через синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника;
— чему равны значения синуса, косинуса, тангенса и котангенса углов 30°, 45° и 60°.
Решать соответствующие задачи на вычисление и доказательство
|
21
|
Тригонометрические функции острого угла в прямоугольном треугольнике.
|
1
|
18.11
|
|
22
|
Тригонометрические функции острого угла в прямоугольном треугольнике.
|
1
|
23.11
|
|
23
|
Тригонометрические функции острого угла в прямоугольном треугольнике.
|
1
|
25.11
|
|
24
|
Тригонометрические функции тупого угла в прямоугольном треугольнике.
|
1
|
30.11
|
|
25
|
Тригонометрические функции тупого угла в прямоугольном треугольнике.
|
1
|
02.12
|
|
26
|
Тригонометрические функции тупого угла в прямоугольном треугольнике.
|
1
|
07.12
|
|
27
|
Вычисление элементов треугольников с использованием тригонометрических соотношений.
|
1
|
09.12
|
|
28
|
Вычисление элементов треугольников с использованием тригонометрических соотношений.
|
1
|
14.12
|
|
29
|
Вычисление элементов треугольников с использованием тригонометрических соотношений.
|
1
|
16.12
|
|
30
|
Теорема Пифагора.
|
1
|
21.12
|
|
31
|
Теорема Пифагора.
|
1
|
23.12
|
|
32
|
Теорема Пифагора.
|
1
|
11.01
|
|
33
|
Контрольная работа № 3 по теме «Основные тригонометрические тождества»
|
1
|
13.01
|
|
IV. Векторы и координаты на плоскости
|
20
|
|
|
|
|
|
Координаты
|
11
|
|
|
|
|
34
|
Анализ контрольной работы. Основные понятия: координаты вектора
|
1
|
18.01
|
|
ММС
|
Объяснять, что такое:
— декартова система координат, ось абсцисс, ось ординат, координаты точки, начало координат;
— уравнение фигуры;
— угловой коэффициент прямой;
— вектор и его направление, одинаково направленные и противоположно направленные векторы;
— абсолютная величина (модуль) вектора, координаты вектора;
— нулевой вектор;
— равные векторы;
— угол между векторами;
— сумма и разность векторов;
— произведение вектора и числа;
— скалярное произведение векторов;
— единичный и координатные векторы;
— проекции вектора на оси координат.
Формулировать и доказывать:
— «правило треугольника»;
— теорему об абсолютной величине и направлении вектора 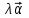 ; ;
— теорему о скалярном произведении векторов.
Знать:
— формулы координат середины отрезка;
— формулу расстояния между точками;
— уравнение окружности, в том числе с центром в начале координат;
— уравнение прямой, условие параллельности прямой одной из осей координат, условие прохождения её через начало координат;
— чему равен угловой коэффициент прямой; — что для 0 < α < 180° 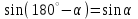 , , 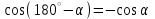 , , 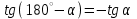 , , 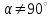 , , 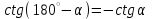 . .
Решать задачи на вычисление, нахождение и доказательство
|
35
|
Основные понятия: координаты вектора.
|
1
|
20.01
|
|
36
|
Основные понятия: расстояние между точками.
|
1
|
25.01
|
|
37
|
Основные понятия: расстояние между точками.
|
1
|
27.01
|
|
38
|
Основные понятия: координаты вектора, расстояние между точками.
|
1
|
01.02
|
|
39
|
Координаты середины отрезка.
|
1
|
03.02
|
|
40
|
Координаты середины отрезка.
|
1
|
08.02
|
|
41
|
Координаты середины отрезка.
|
1
|
10.02
|
|
42
|
Уравнения фигур
|
1
|
15.02
|
|
43
|
Уравнения фигур
|
1
|
17.02
|
|
44
|
Уравнения фигур
|
1
|
22.02
|
|
|
Векторы
|
9
|
|
|
45
|
Понятие вектора.
|
1
|
24.02
|
|
46
|
Действия над векторами.
|
1
|
01.03
|
|
47
|
Действия над векторами.
|
1
|
03.03
|
|
48
|
Использование векторов в физике, разложение вектора на составляющие
|
1
|
08.03
|
|
49
|
Разложение вектора на составляющие.
|
1
|
10.03
|
|
50
|
Скалярное произведение векторов.
|
1
|
15.03
|
|
51
|
Скалярное произведение векторов.
|
1
|
17.03
|
|
52
|
Скалярное произведение векторов.
|
1
|
22.03
|
|
53
|
Контрольная работа № 4 по теме «Векторы»
|
1
|
24.03
|
|
V.Геометрические преобразования
|
9
|
|
|
|
|
|
Преобразования
|
1
|
|
|
|
Объяснять, что такое:
— преобразование фигуры, обратное преобразование;
— движение;
— преобразование симметрии относительно точки, центр симметрии;
— преобразование симметрии относительно прямой, ось симметрии;
— поворот плоскости, угол поворота;
— параллельный перенос.
Формулировать и доказывать, что:
— точки прямой при движении переходят в точки прямой с сохранением их порядка;
— преобразования симметрии относительно точки и относительно прямой являются движениями. Формулировать свойства:
— движения;
— параллельного переноса.
Решать задачи, используя приобретённые знания
|
54
|
Понятие преобразования.
|
1
|
05.04
|
|
ММС
|
|
Движения
|
8
|
|
|
55
|
Осевая и центральная симметрия.
|
1
|
07.04
|
|
56
|
Осевая и центральная симметрия.
|
1
|
11.04
|
|
57
|
Поворот и параллельный перенос.
|
1
|
14.04
|
|
58
|
Поворот и параллельный перенос.
|
1
|
19.04
|
|
59
|
Комбинации движений на плоскости и их свойства.
|
1
|
21.04
|
|
60
|
Комбинации движений на плоскости и их свойства.
|
1
|
26.04
|
|
61
|
Комбинации движений на плоскости и их свойства.
|
1
|
28.04
|
|
62
|
Контрольная работа № 5 по темам «Декартовы координаты на плоскости», «Движение»
|
1
|
03.05
|
|
|
Итоговое повторение
|
6
|
|
|
|
|
63
|
Анализ контрольной работы. Итоговое повторение раздела «Четырёхугольники»
|
1
|
05.05
|
|
|
|
64
|
Итоговое повторение раздела «Теорема Пифагора»
|
1
|
10.05
|
|
65
|
Итоговое повторение раздела «Декартовы координаты на плоскости»
|
1
|
12.05
|
|
66
|
Итоговое повторение раздела «Движение»
|
1
|
17.05
|
|
67
|
Итоговое повторение раздела «Векторы»
|
1
|
19.05
|
|
68
|
Итоговое повторение курса геометрии 8 класса.
|
1
|
24.05
|
|
|
ИТОГО
|
68
|
|
|
 Скачать 42.2 Kb.
Скачать 42.2 Kb.
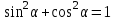 ,
,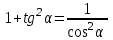 ,
,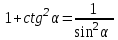 ,
,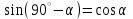 ,
,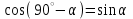 .
.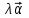 ;
; 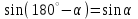 ,
, 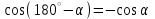 ,
, 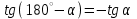 ,
, 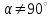 ,
, 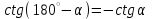 .
.