безбородко. Учебник для слушателей и курсантов высших пожарнотехнических образовательных учреждений
 Скачать 40.6 Mb. Скачать 40.6 Mb.
|
|
6.1.3. Сила сопротивления подъему пожарного автомобиля Сила сопротивления подъему ПА Pi , Н, является составляющей силы веса (см. рис. 6.1): 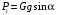 . (6.15) . (6.15)Вместо αможет быть задан уклон i. Уклон может быть выражен в процентах i % и промилле i, ‰. Уклон дороги i представляет собой отношение (см. рис. 6.1) 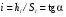 , (6.16) , (6.16)где hi– превышение дороги; Si– заложение дороги. Между i, i % и zi ‰ существует соотношение 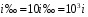 . (6.17) . (6.17) При малых углах подъема дороги ( 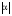 < 10°)tgα ≈ sin αможно считать, что < 10°)tgα ≈ sin αможно считать, что 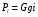 . (6.18) . (6.18)Мощность Ni, кВт, необходимая для преодоления силы сопротивления подъему АТС, определяется по формуле 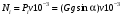 , (6.19) , (6.19)здесь G в кг; g в м/с2; v в м/с. При 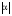 < 10° можно считать, что < 10° можно считать, что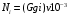 . (6.20) . (6.20)6.1.4. Сила сопротивления воздуха Движущийся ПА часть мощности двигателя расходует на перемещение воздуха и его трение о поверхность АТС. Сила сопротивления воздуха Рв, Н, определяется по формуле 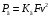 , (6.21) , (6.21)где F – лобовая площадь, м2; Кв– коэффициент обтекаемости, (Нс2)/м4; v – скорость автомобиля, м/с. Лобовой площадью называют площадь проекции АТС на плоскость, перпендикулярную продольной оси автомобиля. Лобовую площадь можно определить по чертежам общего вида ПА. При отсутствии точных размеров ПА лобовая площадь вычисляется по формуле 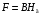 , (6.22) , (6.22)где В – колея, м; Нг – габаритная высота ПА, м. Коэффициент обтекаемости определяется для каждой модели АТС экспериментально, при продувке автомобиля или его модели в аэродинамической трубе. Коэффициент Кв равен силе сопротивления воздуха, создаваемой 1 м2 лобовой площади автомобиля при его движении со скоростью 1 м/с. Для ПА на шасси грузовых автомобилей Кв= 0,5 – 0,6 (Нс2)/м4, для легковых Кв = 0,2 – 0,35 (Нс2)/м4, для автобусов Кв = 0,4 – 0,5 (Нс2/м4. При прямолинейном движении и отсутствии бокового ветра силу Рвпринято направлять вдоль продольной оси АТС, проходящей через центр масс автомобиля или через геометрический центр лобовой площади. Мощность Nв, кВт, необходимая для преодоления силы сопротивления воздуха, определяется по формуле 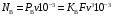 . (6.23) . (6.23)Здесь F в м2, v в м/с. При v≤ 40 км/ч сила сопротивления воздуха мала и при расчетах движения ПА на этих скоростях ее можно не учитывать. 6.1.5. Сила инерции Часто движение ПА удобнее рассматривать в системе отсчета, жестко связанной с автомобилем. Для этого к ПА необходимо приложить инерционнные силы и моменты. В теории АТС инерционные силы и моменты при прямолинейном движении автомобиля без колебаний в продольной плоскости принято выражать силой инерции Рj, Н: 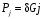 , (6.24) , (6.24)где j – ускорение центра масс АТС, м/с2. Сила инерции направлена параллельно дороге через центр масс АТС в сторону, противоположную ускорению. Для учета увеличения силы инерции из-за наличия у АТС вращающихся масс (колес, деталей, трансмиссии, вращающихся деталей двигателя) введем коэффициент δ. Коэффициент δ учета вращающихся масс показывает, во сколько раз энергия, затрачиваемая при разгоне вращающихся и поступательно движущихся деталей АТС, больше энергии, необходимой для разгона АТС, все детали которого движутся только поступательно. При отсутствии точных данных коэффициент δ для ПА можно определять по формуле 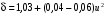 . (6.25) . (6.25)Мощность Nj, кВт, необходимая для преодоления силы инерции, определяется по формуле 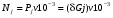 . (6.26) . (6.26)6.1.6. Нормальные реакции опорной поверхности колес При движении ПА нормальные реакции Rn изменяются. Уменьшение или увеличение нагрузки на п-е колесо при движении АТС характеризуется коэффициентом λп изменения нормальной реакции 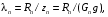 (6.27) (6.27)где zn – нормальная реакция опорной поверхности (нагрузка) n-го колеса при стоянке АТС на горизонтальной дороге; Gn – масса АТС, сила веса, которая создает нагрузку zn. Если нормальные реакции колес левой и правой стороны одной оси ПА равны, то коэффициент λn характеризует также и изменение нагрузки на ось. Распределение силы веса (Gg) между колесами ПА зависит от положения центра масс автомобиля, жесткости подвески и рамы, давления воздуха в шинах. При вычислении zn влиянием всех факторов, кроме положения центра масс, обычно пренебрегают. Для двухосного автомобиля нагрузки zn вычисляют по формулам (рис. 6.5): 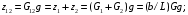 (6.28) (6.28)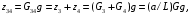 (6.29) (6.29)Рис. 6.5. Определение координат центра масс пожарного автомобиля: 1 – платформа весов При компоновке ПА добиваются равного распределения силы веса между колесами одной оси: 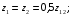 (6.30) (6.30)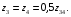 (6.31) (6.31) Из-за обязательного выполнения требований по равенству нагрузки на левые и правые колеса одной оси в технических характеристиках АТС и ПА принято указывать только G, расстояние между осями и массы, силы веса от которых передаются каждой осью. Для двухосного АТС указываются: G,L и G12, G34 Данные по G12и G34, которые приводятся в технических характеристиках АТС, определяются, как правило, экспериментально. Для аналитического определения G12 и G34 необходимо знать расстояния а, L или b, L. Основная погрешность аналитического определения G12 и G34 для двухосного автомобиля связана с ошибками в вычислении положения центра масс АТС, координаты которого (a или b) определяются по формулам для вычисления положения центра масс абсолютно твердого тела. Вычисление а или b по этим формулам приводит к ошибке до 10–15 %. Для экспериментального определения z12 или z34 колеса передней или задней оси ПА устанавливают на весы (см. рис. 6.5). Для проверки равенств (6.30), (6.31) ПА устанавливают на весы колесами одной стороны. Основные требования при взвешивании: полная комплектация ПА (при отсутствии боевого расчета его имитируют балластом); горизонтальная опорная поверхность колес ПА при взвешивании; расторможенные колеса и нейтральное положение рычага механической коробки передач. Взвешивают ПА, как правило, два раза: первый – при въезде на весы передним ходом, второй – при въезде на весы задним ходом. За зачетные значения G, z12 и z34 принимаются их средние арифметические. По результатам взвешивания судят о возможности эксплуатации ПА. Необходимо выполнение трех основных требований: масса G ПА не должна превышать полной массы базового шасси – собственной массы базового шасси плюс грузоподъемность; распределение массы G между осями ПА (G12 или G34) должно соответствовать распределению между осями полной массы базового шасси; нагрузка на колеса левой и правой стороны ПА должна быть равной. Нагрузки на оси R12 и R34 при движении ПА определяются из уравнений: 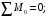  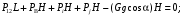 (6.32) (6.32)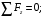 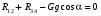 . (6.33) . (6.33)После преобразований уравнений (6.32), (6.33) и подстановки R12 и R34, z12 и z34 формул (6.28), (6.29) в формулу (6.27) получим: 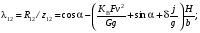 (6.34) (6.34)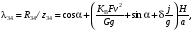 (6.35) (6.35)где α > 0, ј > 0 – при подъеме и разгоне АТС; α < 0, ј < 0 – при спуске и торможении АТС. Анализ формул (6.34) и (6.35) показывает, что при движении на подъеме и разгоне ПА увеличивается нагрузка на заднюю ось и уменьшается на переднюю. При движении на спуске и торможении ПА происходит обратное явление. Этим объясняется, например, подъем передней части ПА, наблюдаемый при разгоне, и наклон ее вниз («клевок») при торможении. При движении по дорогам с асфальтобетонным покрытием коэффициенты λ12 и λ34 ПА могут изменяться в пределах от 0,5 до 1,5. Предельные значения коэффициентов достигаются при движении по крутым уклонам и при интенсивном разгоне или торможении ПА со всеми ведущими осями или при экстренном торможении. 6.1.7. Уравнение силового баланса пожарного автомобиля При использовании метода силового баланса уравнение (6.1) записывается в виде РВ 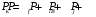 (6.36) (6.36)и называется уравнением силового баланса. Последовательность решения уравнения (6.36) методом силового баланса: 1. По уравнению (6.36) вычисляется суммарная сила тяги ведущих колес, которую необходимо реализовать для движения ПА на заданной передаче (заданном и) в известных дорожных условиях (α, f) со скоростью v и ускорением j. Вычислять необходимую Рк удобнее по формуле 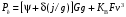 , (6.37) , (6.37)где ψ = fcоsα + sinα – коэффициент сопротивления дороги. Формула (6.37) получена после подстановки в правую часть уравнения (6.36) правых частей формул (6.13), (6.15), (6.21), (6.24) и последующих преобразований. 2. По формуле (6.10) вычисляется максимальная сила тяги Рφ, которую могут обеспечить ведущие колеса ПА по сцеплению с дорогой. Сила Рφ вычисляется с учетом перераспределения нагрузки между колесами ПА. Двухосные и трехосные ПА при движении с подводом крутящего момента двигателя к ведущим колесам задних осей могут обеспечить по сцеплению с дорогой 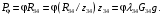 (6.38) (6.38)Использование всех колес ПА для создания силы тяги позволяет увеличить Рφ на 15 – 30 %. Максимальная сила тяги Рφ полнопроводных ПА определяется по формуле 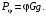 (6.39) (6.39)3. Проверяется выполнение неравенства (6.11). Если неравенство (6.11) не выполняется, то длительное (безостановочное) движение ПА на заданной передаче в известных дорожных условиях (α, f) со скоростью vи ускорением j невозможно. В зависимости от решаемой задачи изменяется один из перечисленных параметров и расчеты повторяются. 4. По формуле (6.4) вычисляется суммарная сила тяги (обозначим ее Ркд), которую может обеспечить двигатель на ведущих колесах ПА. Крутящий момент двигателя Мд определяется по внешней скоростной характеристике (см. рис.5.9) или по формуле (5.8) при частоте вращения коленчатого вала 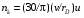 , (6.40) , (6.40)где nд в об/мин; v в м/с; rDв м. 5. Необходимая для движения сила тяги (обозначим ее Ркн), вычисленная по формуле (6.37), сравнивается с силой тяги Ркд , которую может обеспечить двигатель. Если Ркн < Ркд, то движение ПА возможно при неполном открытии дроссельной заслонки (карбюраторный двигатель) или при неполной подаче топлива (дизель). Если Ркн = Ркд , то уравнение (6.36) решено и движение ПА возможно только при полном открытии дроссельной заслонки или полной подаче топлива, т. е. при использовании внешней скоростной характеристики двигателя. Если Ркн > Ркд, то движение ПА при заданных условиях (и, α, f, v, j) невозможно – двигатель не может обеспечить необходимую силу тяги на ведущих колесах. Один из параметров – и, α, f, v или j изменяется и расчеты повторяются с п. 1. Методом силового баланса можно определить vmaxиvmin. Для этого при расчетах необходимо изменять и и v при j = 0, α = 0. Для определения αmax необходимо изменять v и α при движении ПА на первой передаче и Рв ≈ 0. Для определения tv метод силового баланса не применяют из-за большого объема расчетов. 6.1.8. Уравнение мощностного баланса пожарного автомобиля Метод мощностного баланса основан на анализе использования мощности двигателя при движении ПА. По аналогии с уравнением силового баланса уравнение мощностного баланса ПА можно записать в следующем виде Nп.о NB 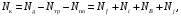 (6.41) (6.41)где Nд – мощность, которая передается от двигателя к трансмиссии ПА; Nтр – мощность, затрачиваемая на преодоление трения в трансмиссии; Nп.о – мощность, затрачиваемая на привод пожарного оборудования (например, насоса, механизма прокладки и сборки рукавных линии) при движении ПА. После учета расхода мощности двигателя на работу дополнительного оборудования базового шасси (коэффициента Кс) и на трение в трансмиссии (учитывается коэффициентом η) формулы (6.14), (6.19), (6.23) и (6.26), уравнение (6.41) можно преобразовать к виду 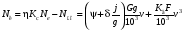 . (6.42) . (6.42)Графическое решение уравнения мощностного баланса для определения скорости движения ПА на первой и второй передачах с одновременной подачей воды из цистерны через лафетный ствол приведено на рис. 6.6. 2 3 v v2 v1 N 4 Рис. 6.6. Графическое решение уравнения мощностного баланса пожарного автомобиля: - движение на первой передаче; --- движение на второй передаче; 1 – Ne; 2 – KeηNe; 3 – Nк = KeηNe – Nn; 4 – Nψ Внешняя скоростная характеристика двигателя Ne(n) (см. рис. 5.9) построена в координатах N – v. При построении зависимости Ne(v) (см. рис. 6.6, кривая 1) предполагается, что нет пробуксовки ведущих колес ПА и для пересчета nд в v, и наоборот, можно использовать формулу (6.40). Вниз от Ne(v) отложена мощность, которая затрачивается на преодоление трения в трансмиссии и на обеспечение работы дополнительного оборудования базового шасси. Для движения ПА и привода насоса может быть использована мощность КсηNe (рис. 6.6, кривая 2). Мощность Nпо отложена вниз от мощности КсηNe. Мощность Nпо, затрачиваемая на привод пожарного центробежного насоса, пропорциональна третьей степени частоты вращения рабочего колеса насоса. Зависимость Ne(n), а следовательно, и зависимость КсηNe в координатах N– v (рис. 6.6, поз. 2) также представляет собой многочлен третьей степени (формула (5.11)). Поэтому зависимость мощности, которую может обеспечить двигатель на ведущих колесах ПА (рис. 6.6, кривая 3), – кубическая парабола, вид которой зависит: от внешней скоростной характеристики двигателя Ne(nд), от передаточного числа и и коэффициента полезного действия ηтрансмиссии ПА на включенной передаче, от передаточного числа итн и коэффициента полезного действия ηтн трансмиссии пожарного насоса, от подачи Qн, напора Hн и коэффициента полезного действия ηн насоса. Если принять, что коэффициент f – величина постоянная и сила сопротивления воздуха при движении на первой и второй передаче пренебрежимо мала, то правая часть уравнения (6.42) представляет собой наклонную прямую (рис. 6.6, прямая 4), проходящую через начало координат. При полном открытии дроссельной заслонки карбюраторного двигателя или при полной подаче топлива дизельного двигателя движение ПА на первой и второй передачах не может быть более скоростей v1 и v2. Скорости v1 и v2 определяются по точкам пересечения (см. рис. 6.6). Для равномерного движения в тех же условиях со скоростью, меньшей v1 или v2, водитель должен прикрыть дроссельную заслонку карбюраторного двигателя или уменьшить подачу топлива дизельного двигателя, что приведет к уменьшению частоты вращения коленчатого вала двигателя и, как следствие, к уменьшению подачи Qни напора Нн насоса. Если на ПА установлена коробка отбора мощности (КОМ) с постоянным передаточным числом, то водителю сложно одновременно обеспечить и необходимую скорость движения, и необходимую подачу воды из лафетного ствола. Для того чтобы обеспечить водителю возможность одновременного выбора требуемых скорости движения и подачи воды из лафетного ствола, необходимо или устанавливать КОМ с переменным передаточным числом, или устанавливать на ПА такие двигатели и насосы, в графике мощностного баланса которых кривая 3 на первой и второй передачах не пересекают прямую 4.Метод мощностного баланса удобно использовать при выборе двигателя базового шасси ПА. Использовать этот метод для определения vmax, tυ ,аmax, vminнецелесообразно, так как приходится дополнительно вычислять Рк, Рφ проверять выполнение неравенства (6.11). |
