Дубровский В.И., Федорова В.Н. Биомеханика. Учебник для вузов

• Название: Учебник для вузов
• Анкор: Дубровский В.И., Федорова В.Н. Биомеханика.doc
• Дата: 28.01.2017
• Размер: 6.47 Mb.
• Имя файла: Дубровский В.И., Федорова В.Н. Биомеханика.doc
• Тип: Учебник; #922
• страница: 26 из 65

8.4. Медицинские аспекты

Величины перегрузок могут колебаться в пределах допустимой переносимости, но они во всех случаях не должны нарушать кровоснабжения мозга.

Как показали многочисленные исследования, ускорения в направлении «голова—ноги» вызывают отток крови от головы и приводят к заметным нарушениям деятельности мозга. Ускорения в направлении «грудь—спина» переносятся человеком гораздо легче и кровоснабжение мозга если и нарушается, то в заметно меньших пределах.

При перегрузках нарушается координация произвольных движений. При этом пределы нарушений зависят от состояния и тренированности лица, оказавшегося в этих условиях, и пропорциональны логарифму ускорения силы тяжести. Способность человека восстанавливать координацию движений при систематическом выполнений навыка в условиях перегрузок может служить отправным положением для разработки общих основ специальной физической подготовки космонавтов, но это не является предметом рассмотрения в данном учебнике.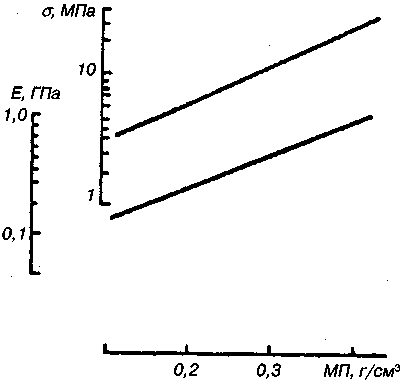



Рис. 8.7. Зависимость механических свойств костных губчатых структур

от минеральной плотности МП: σ— разрушающее напряжение,

Е — модуль упругости
Как было показано выше, физические нагрузки на организм человека, естественные на Земле, в космосе отсутствуют. Поэтому во время космических полетов возникает остеодистрофия, связанная с состоянием невесомости. Снижается резистентность (сопротивляемость) костно-опорного аппарата человека действию ударных нагрузок. Основным следствием изменения биомеханических свойств костной ткани, в первую очередь спонгиозной, является снижение ее минеральной плотности или насыщенности. На рис. 8.7 приведена зависимость механических свойств костных структур от их минеральной плотности.

С уменьшением минеральной плотности линейно снижаются предел прочности и модуль упругости. В условиях невесомости проявляется в основном отрицательный баланс кальция и снижение минеральной плотности костной ткани некоторых элементов скелета. Потери минеральных компонентов из всех костей скелета составляют в среднем 0,4%. Однако по высоте скелета минеральная плотность изменялась не одинаково. Начиная с уровня поясничных позвонков и ниже, минеральная плотность костной ткани снижалась. Время восстановления минеральной плотности поясничных позвонков после полета может в 2—3 раза превышать длительность полета. Этот факт позволяет спланировать режим послеполетной реабилитации космонавтов.

Установлено, что условия невесомости с точки зрения минерализации можно моделировать. Оказалось, что потери кальция в условиях космического полета соответствуют потерям, которые наблюдаются при длительном постельном режиме. Это позволяет рассматривать постельный режим как адекватную модель невесомости применительно к костной системе.

Неблагоприятное влияние реальной и моделируемой постельным режимом невесомости на механические характеристики костей подтверждено экспериментами с крысами на биоспутниках и опытами с биоптатами костной ткани, взятыми у добровольцев после длительной гипокинезии (ограниченного движения).

В качестве средств профилактики костной атрофии можно применять искусственное нагружение, которое обеспечит уровень напряжений в скелете, соответствующий земным гравитационным нагрузкам или достаточно продолжительное воздействие (например, одночасовое спокойное стояние при постельном режиме в остальное время предотвращает отрицательный кальцевый баланс).

8.5. Применение законов динамики для анализа движений спортсменов

Разберем некоторые примеры, показывающие, каким образом законы динамики применяются -для анализа сложных движений и вычисления сил, нагружающих суставы, сухожилия и мышцы.

На рис. 8.8. показан стартующий бегун. На него действуют сила тяжести mg и реакция опоры R, сообщающие центру масс бегуна ускорение а.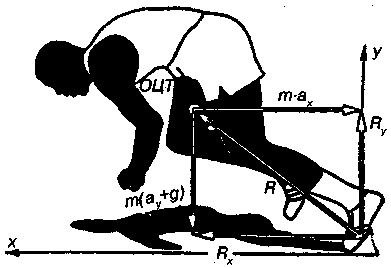



Рис. 8.8. Силы, действующие на тело спринтера при отталкивании во время старта
Воспользуемся неинерциальной системой отсчета, связанной с центром масс. В этой системе центр масс покоится. Согласно принципу Д^,Аламбера к реальным силам следует добавить фиктивную силу инерции F_И = -т·а и записать условие покоя:
В проекциях на координатные оси это равенство запишется в виде системы двух уравнений:


где R_x, R_y— составляющие реакции опоры; а_yи а_х— вертикальная и горизонтальная составляющие ускорения центра масс в момент старта.

Эти уравнения можно использовать для решения двух задач:

• зная силы, действующие на тело, описать движение центра масс;

• зная ускорение тела (используя различные способы регистрации, например, киносъемку), определить вызвавшие его силы.

Вычислим силу тяги мышц f_m, нагружающих ахиллово сухожилие при старте бегуна. На рис. 8.9 показаны стопа и действующие на нее силы.

Это реакция опоры R, сила тяжести m_cT·g, сила тяги мышц F_m и сила, нагружающая голеностопный сустав, F. Кроме того, на стопу действуют силы пассивного сопротивления, связанные с деформацией соединительных тканей и с силой трения в суставе.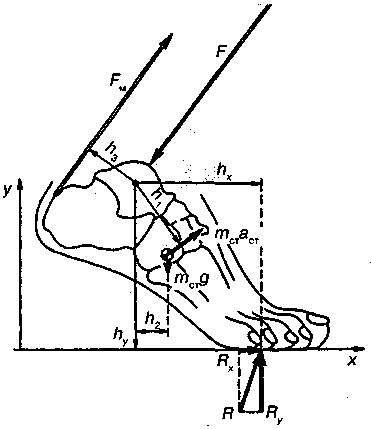


Рис. 8.9. Силы, действующие на стопу спортсмена при отталкивании
Обозначим ускорение голеностопного сустава а_ст и воспользуемся связанной с ним неинерциальной системой отсчета. В этой системе сустав неподвижен, а стопа вращается вокруг него с некоторым угловым ускорением ε. Согласно принципу Д'Аламбера к реальным силам следует добавить фиктивную силу инерции F_и= —т· а_сти записать условие вращения:


где m_ст, I_ст — масса и момент инерции стопы (относительно голеностопного сустава); М_c, — момент сил пассивного сопротивления; М_м— момент силы тяги мышц (F_м), нагружающих ахиллово сухожилие; h_х, h_у, h_1, h₂— плечи сил.

Проанализируем левую часть этого уравнения. Сила тяжести (m_ст·g) и сила инерции (m_ста_ст), действующие на стопу, малы по сравнению с силами реакции опоры (R_xи R_y ), а их плечи (h₂и h₂) меньше плеч сил реакции опоры(h_xи h_y). Поэтому моментами этих сил (—m_n·g·h₂и m_n·a_ст·h₁) можно пренебречь. Момент сил пассивного сопротивления в суставе С/И.) также незначителен по сравнению с моментами сил реакции опоры.

Правую часть уравнения можно принять равной нулю, поскольку согласно расчетам и измерениям, произведение момента инерции стопы^; на ее угловое ускорение (I_ст·ε_ст) мало по сравнению с основными слагаемыми левой части. Поэтому уравнение (8.10) упрощается:



Отсюда получаем соотношение для момента силы тяги мышц:


Момент силы тяги мышц равен произведению силы на плечо:

а составляющие реакции опоры определяются системой (8.9):



Подставив эти выражения в (8.11), получим:



Отсюда находим формулу для расчета приближенного значения силы тяги мышц, нагружающих ахиллово сухожилие: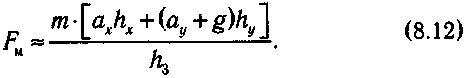



Вычислим ориентировочное значение этой силы. Для взрослого человека можно принять т = 70 кг, h_y=12 см, h_x=10 см, h₃ = 6 см. Измеренные значения составляющих ускорения центра масс равны а 1,5g, a g. Подставив эти значения в (8.12) получим:



Полученное значение близко к максимально допустимой нагрузке для ахиллова сухожилия, которая составляет примерно 5000 Н.

Проведя аналогичные расчеты, можно получить значение для силы F, которой нагружен голеностопный сустав. В данном случае получается значение близкое 3·mg.