Дубровский В.И., Федорова В.Н. Биомеханика. Учебник для вузов
 Скачать 6.47 Mb. Скачать 6.47 Mb.
|
9.5. Соударение предмета с движущимся массивным препятствиемМногие удары в игровых видах спорта можно рассматривать как столкновение мяча с движущейся «преградой». К таким соударениям, например, относятся прием мяча в теннисе, футболе, волейболе и т.п. Вследствие того, что конечность, наносящая удар, превращается в жесткую кинематическую цепь, удар мяча воспринимает не отдельное звено, а практически все тело. Масса тела во много раз больше массы мяча и его (тела) скорость в результате соударения практически не меняется. Для описания таких соударений существуют простые и удобные формулы. Мы рассмотрим два случая. 1. Перед ударом мяч и препятствие движутся навстречу друг другу. Скорость мяча — v0, скорость препятствия — и (рис. 9.17, а). Обозначим коэффициент восстановления скорости мяча k. Тогда скорость мяча после удара (рис. 9.17, б) определяется формулой v = k·v0+(k + 1)·u. (9.17) Во встречных ударах скорость после удара может оказаться больше, чем до удара. В частности, при абсолютно упругом ударе (k = 1) она возрастет на 2и. 2. Перед ударом мяч движется на «убегающее» от него препятствие. Скорость мяча — v0, скорость препятствия — и (рис. 9.18, а). Обозначим коэффициент восстановления скорости мяча k. Тогда скорость мяча после удара (рис. 9.18, б) определяется формулой v = k·v0─(k + 1)∙u. (9.18)  Рис. 9.17. Встречное соударение мяча с движущейся преградой: а) до удара, б) после  Рис. 9.18. Соударение мяча с «убегающей» преградой: а) до удара, б) после При соударениях «вдогонку» скорость после удара всегда меньше чем до удара. Это используют для «укрощения» мяча при приеме. Например, футболист, принимающий мяч на грудь и сбрасывающий его себе под ноги, в момент приема мяча резко подает корпус назад. 9.6. Закон сохранения момента импульсаВ подразделе 7.2 было введено понятие момента импульса произвольного тела и получено уравнение (7.6), описывающее изменение момента импульса под действием моментов сил. Если внешние силы не создают вращательного момента (М = 0), то уравнение (7.6) принимает вид, который выражает важный закон сохранения момента импульса: dL = 0→L = const. (9.19) Если суммарный момент внешних сил, действующих на тело, вращающееся вокруг оси, равняется нулю, то его момент импульса остается постоянным. Этот закон применяется при рассмотрении вращения системы тел вокруг общей оси. Примеры, иллюстрирующие этот закон, представлены на рис. 9.19. 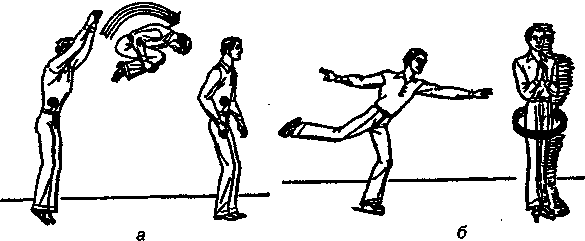 Рис. 9.19. Примеры проявления закона сохранения момента импульса: а) гимнаст, б) фигурист Гимнаст, выполняющий сальто (рис. 9.19, а), в начальной фазе сгибает колени и прижимает их к груди, уменьшая тем самым момент инерции и увеличивая угловую скорость вращения вокруг горизонтальной оси. В конце прыжка его тело выпрямляется, момент инерции возрастает, угловая скорость уменьшается. Фигурист, совершающий вращение вокруг вертикальной оси (рис. 9.19, б), в начале вращения приближает руки к корпусу, тем самым уменьшая момент инерции и увеличивая угловую скорость. Так, если момент инерции фигуриста уменьшается в два раза, то во столько же раз увеличивается его угловая скорость. В конце вращения происходит обратный процесс: при разведении рук увеличивается момент инерции и уменьшается угловая скорость, что позволяет легко остановиться. Во время прыжка в воду с трамплина, толчок, испытываемый спортсменом в момент отрыва от гибкой доски, «закручивает» его, т. е. сообщает прыгуну начальный запас момента импульса относительно его ЦМ. Прежде чем прыгнуть в воду, прыгун совершает один или несколько оборотов с большой угловой скоростью; затем он вытягивает руки, увеличивая тем самым свой момент инерции и, следовательно, снижая свою угловую скорость до совсем небольшой величины перед входом в воду. Момент инерции при этом может измениться в 3,5 раза. Глава 10 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ |
