Дубровский В.И., Федорова В.Н. Биомеханика. Учебник для вузов
 Скачать 6.47 Mb. Скачать 6.47 Mb.
|
10.2.Вынужденные колебания. РезонансВ некоторых случаях колебания могут происходить под действием внешних сил. Вынужденные колебания возникают в системе при участии внешней силы, изменяющейся по периодическому закону. Рассмотрим случай, когда на тело помимо упругой силы F и силы трения Fтрдействует еще и вынуждающая гармоническая сила fb= F0·соs(ωв ·t), где F0— амплитуда силы; ωв — круговая частота ее колебаний. Запишем дифференциальное уравнение движения, вытекающее из второго закона Ньютона: или где Можно показать, что для больших значениях t решение этого уравнения определяется формулой: где φв — разность фаз между силой Fви смещением х. Таким образом, установившиеся вынужденные колебания, происходящие под воздействием гармонически изменяющейся силы, являются тоже гармоническими. Их частота равна частоте вынуждающей силы. Амплитуда А установившихся вынужденных колебаний зависит от собственной частоты колебаний, массы материальной точки, амплитуды и частоты вынуждающей силы и коэффициента затухания: Вибрация Одним из проявлений вынужденных колебаний является вибрация. Вибрация используется при массаже. При ручном массаже массируемые ткани приводятся в колебательное движение при помощи рук массажиста. При аппаратном массаже используются вибрационные аппараты, которые подразделяются на аппараты для общей вибрации, вызывающие сотрясение всего тела (вибрационные «стул», «кровать», «платформа» и др.) и аппараты местного вибрационного воздействия. Резонанс Если ω0 и β для системы заданы, то амплитуда вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Само явление — достижение максимальной амплитуды вынужденных колебаний при определенном значении частоты вынуждающей силы называется резонансом. Резонансную круговую частоту можно найти, если определить условие минимума знаменателя в (10.20): При этой частоте имеет место максимум амплитуды вынужденных колебаний, определяемый формулой: 10.3. Сложение гармонических колебаний, направленных по одной прямойПусть тело одновременно участвует в двух колебательных движениях, происходящих вдоль одной линии. Требуется записать закон, по которому изменяется смещение тела в этом случае. Приведем без вывода решение этой задачи для случая, когда частоты обоих колебаний одинаковы. Полное смещение тела х равно сумме двух смещений: Можно показать, что в этом случае получается гармоническое колебание с такой же частотой: амплитуда и начальная фаза которого определяются формулами: 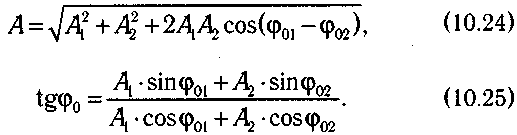 10.4. Сложное колебание. Разложение сложного колебания на простые составляющие. Гармонический спектрСложное периодическое движение — сложное колебание — можно представить в виде суммы гармонических колебаний. Существуют математические методы обработки сложных колебаний. Фурье предложил метод разложения любой периодической функции в ряд гармонических функций, периоды которых кратны периоду сложного колебания. Разложение сложного колебания на гармонические колебания называется гармоническим анализом. Совокупность гармонических колебаний, на которые разложено сложное колебание, называется гармоническим спектром сложного колебания. Пример сложного колебания x(t), которое раскладывается на сумму двух гармонических колебаний, представлен на рис. 10.4. Анализ колебаний, создаваемых телом человека или его отдельными частями, широко используется. При ходьбе, беге центр масс человека совершает движения по кривой, которую часто можно представить синусоидой, амплитуда которой ориентирована вертикально. Колебательные движения совершают участки сердца и легких спортсмена на перекладине и на батуте. 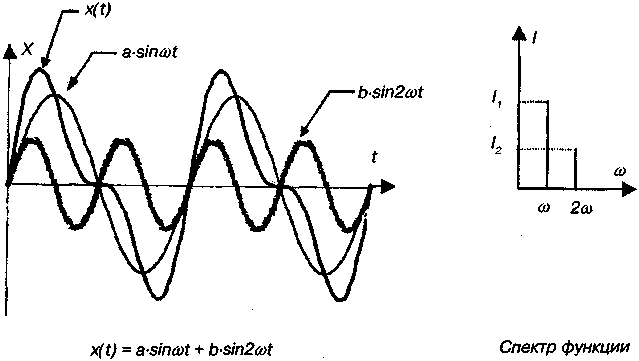 Рис. 10.4. Сложное колебание и его спектр На анализе сложных колебаний основана статокинезиметрия— метод оценки способности спортсмена сохранять вертикальную позу. В эту группу методов входит и стабилография — метод оценки способности спортсмена удерживать проекцию центра масс в пределах координат границы площади опоры. Данный метод реализуется с помощью стабилографа, основной частью которого является стабилоплатформа, на которой находится спортсмен во время испытаний. При поддержании вертикальной позы центр масс человека совершает сложные колебания. Стабилоплатформа содержит тензодатчики, регистрирующие малейшее изменение координат центра масс на плоскость опоры. Автоматически записывается стабилограмма — траектория перемещения центра масс, зависящая от сложного колебательного движения центра масс. Осуществляется спектральный анализ этих сложных колебаний. По гармоническому спектру можно судить об особенностях вертикального положения в норме и при отклонениях от нее. Данный метод эффективен при оценке результатов соответствующих тренировочных методик. Теория колебаний используется в различных методиках по оценке работы сердца. Сесмокардиография основана на регистрации механических колебаний тела человека, вызванных работой сердца. В этом методе с помощью датчиков, установленных в области основания мечевидного отростка, регистрируется сердечный толчок, обусловленный механической активностью сердца в период изоволюмического сокращения. При этом происходят процессы, связанные с деятельностью волюморецепторов — тканевых механорецепторов сосудистого русла, активирующихся при снижении объема циркулирующей крови. Сейсмокардиосигнал формируют колебания грудины. Баллистокардиография. Метод исследования механических проявлений сердечной деятельности, основанный на регистрации пульсовых микроперемещений тела, обусловленных выбрасыванием толчком крови из желудочков сердца в крупные сосуды. При этом возникает явление отдачи. Тело человека помещают на специальную подвижную платформу, которая в результате отдачи приходит в сложное колебательное движение. Зависимость смещения платформы с телом от времени называется баллистокардиограммой, анализ которой позволяет судить о движении крови и состоянии сердечной деятельности. |
