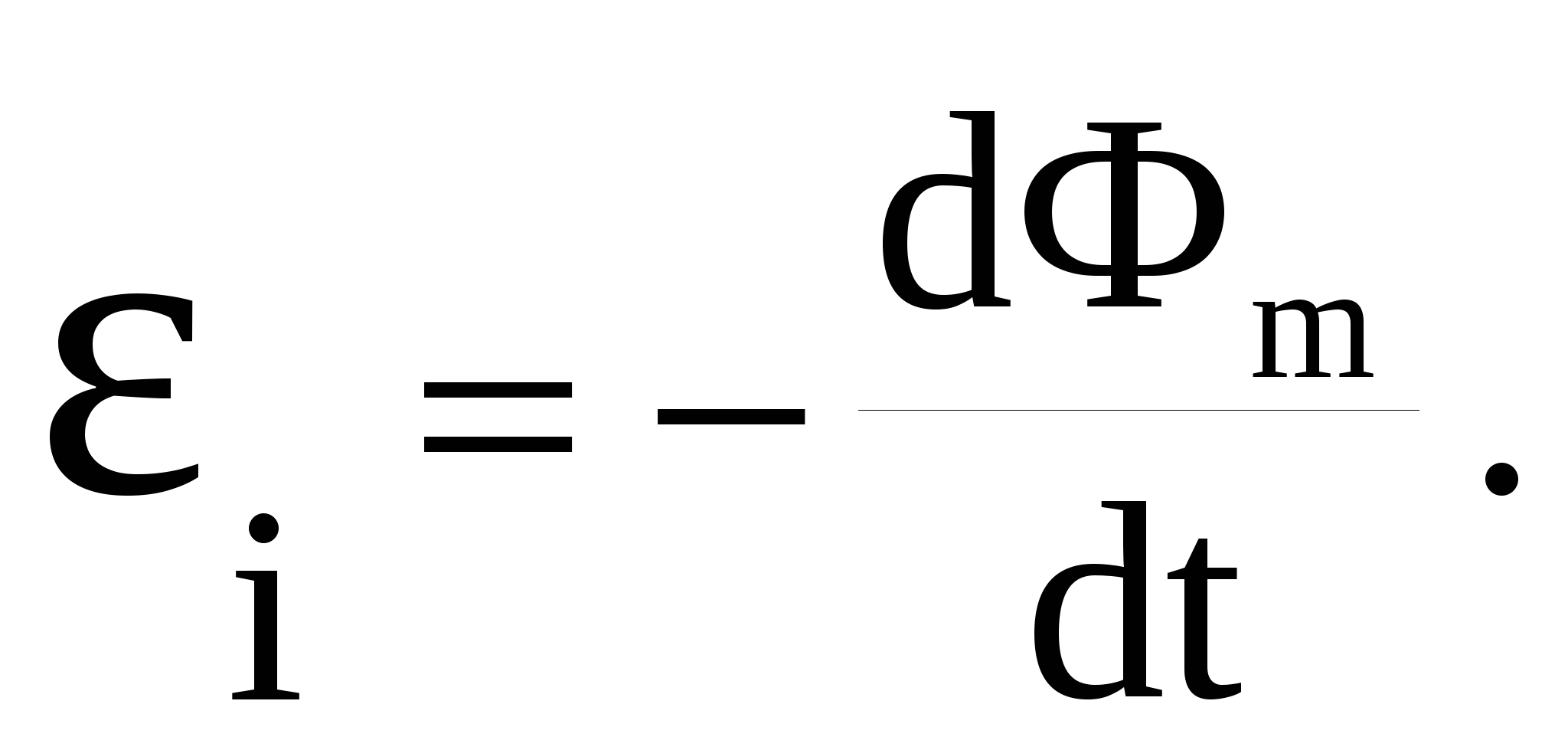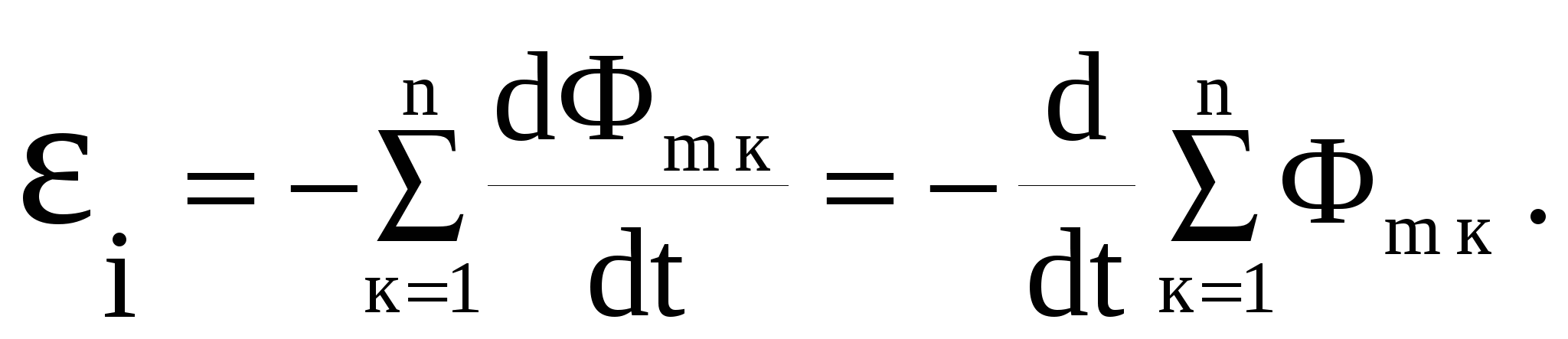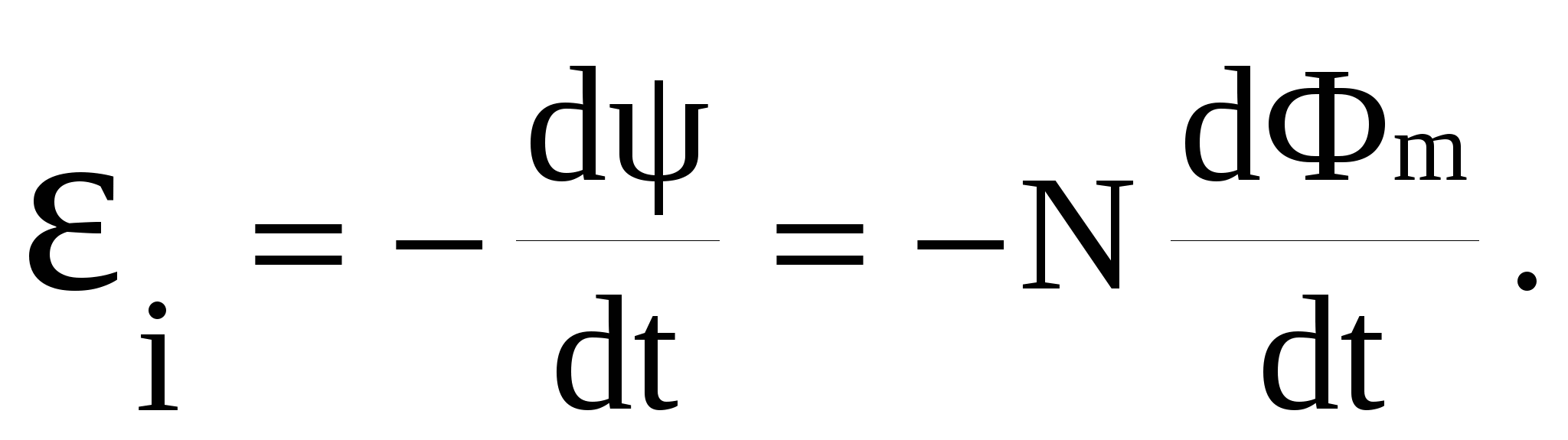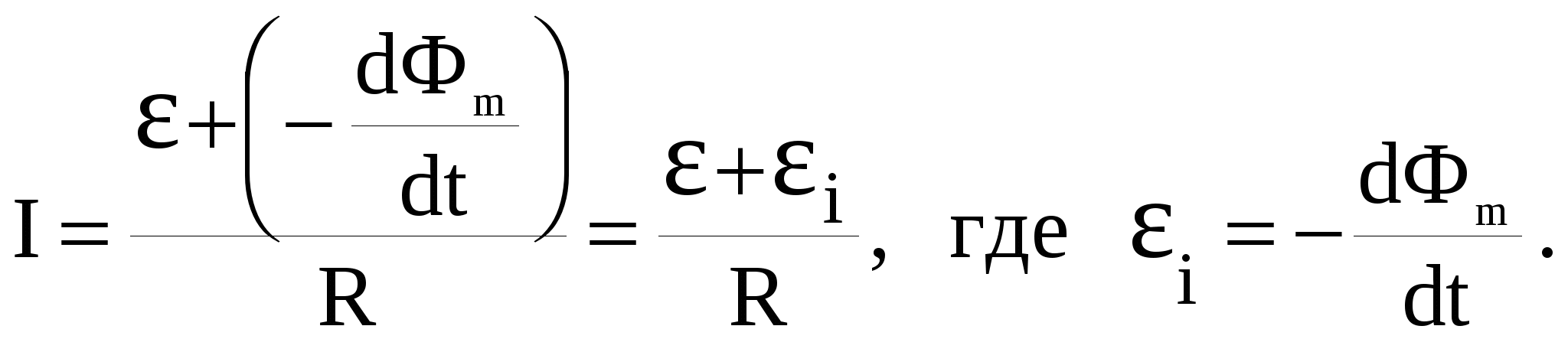|
Учебник по физике магнетизма. Учебник по физике кгтукхти. Кафедра физики. Старостина И. А., Кондратьева О. И., Бурдова Е. В. Для перемещения по тексту электронного учебника можно использовать
2.9. Антиферромагнетики и ферриты. @
В некоторых случаях обменные взаимодействия приводят к тому, что собственные магнитные моменты электронов соседних атомов самопроизвольно ориентируются антипараллельно друг другу. Такие вещества называются антиферромагнетиками, а само явление – антиферромагнетизмом. Существование таких веществ было предсказано Д.Ландау еще в 1933 г. К ним относятся хром, марганец, эрбий, диспрозий, сплавы марганца и меди и др.
Антиферромагнетики обладают малой магнитной восприимчивостью χ и ведут себя как очень слабые парамагнетики. Для них существует определенная температура Тн, называемая точкой Нееля, при которой антипараллельная ориентация спинов исчезает. У некоторых антиферромагнетиков таких температур две – верхняя и нижняя точки Нееля, причем антиферромагнитные свойства наблюдаются только в промежуточной области температур. Выше верхней точки вещество ведет себя как парамагнетик, а ниже нижней точки Нееля - становится ферромагнетиком.
Очень важным достижением в проблеме получения магнитно-мягких материалов явилась разработка ферритов, представляющих собой ферромагнитные полупроводники. Ферриты представляют собой ферромагнитные оксиды металлов, обладающие невысокой коэрцитивной силой и большой остаточной намагниченностью. Это, например, магнетит и гематит, на которых человек впервые познакомился с явлениями магнетизма и которые в течение столетий не находили себе применения, а вошли в практику несколько десятилетий назад. К ферритам относятся химические соединения типа МеО· Fe2O3, где Ме – Мn, Co, Ni, Mg, Cu, Zn, Gd. По своим электрическим свойствам это полупроводники, обладающие высоким удельным сопротивлением. Последнее обстоятельство важно при использовании ферритов в электротехнике. Обычные ферромагнетики нельзя использовать в радиотехнике высоких частот вследствие их большой электропроводности и возникающих из-за этого больших потерь на вихревые токи. Ферриты лишены этого недостатка. Из них изготавливают сердечники трансформаторов и стержни индукционных катушек.
3. ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. @
3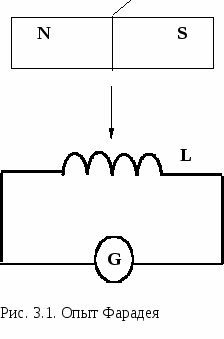 .1. Основной закон электромагнитной индукции. @ .1. Основной закон электромагнитной индукции. @
Величайший физик XIX века Майкл Фарадей считал, что между электрическими и магнитными явлениями существует тесная взаимосвязь. Ампер, Био и другие ученые выяснили одну сторону этой взаимосвязи, с которой мы уже знакомы, а именно – магнитное действие тока. Фарадей предположил, что если вокруг проводника с током существует магнитное поле, то естественно ожидать, что должно происходить и обратное явление – возникновение электрического тока под действием магнитного поля. И вот в 1831 г. Фарадей публикует статью, где сообщает об открытии нового явления – явления электромагнитной индукции.
Опыты Фарадея были чрезвычайно просты. Он присоединял гальванометр G к концам катушки L и приближал к ней магнит (рис.3.1). Стрелка гальванометра отклонялась, фиксируя появление тока в цепи. Ток протекал, пока магнит двигался. При отдалении магнита от катушки гальванометр отмечал появление тока противоположного направления. Аналогичный результат отмечался, если магнит заменяли катушкой с током или замкнутым контуром с током. Движущиеся магнит или проводник с током создают через катушку L переменное магнитное поле. В случае их неподвижности создаваемое ими поле постоянно. Если вблизи замкнутого контура поместить проводник с переменным током, то в замкнутом контуре также возникнет ток. На основе анализа опытных данных Фарадей установил, что ток в проводящих контурах появляется при изменении магнитного потока через площадь, ограниченную этим контуром. Этот ток был назван индукционным. Открытие Фарадея было названо явлением электромагнитной индукции и легло в дальнейшем в основу работы электрических двигателей, генераторов, трансформаторов и подобных им приборов.
Итак, если магнитный поток через поверхность, ограниченную некоторым контуром, изменяется, то в контуре возникает электрический ток. Известно, что электрический ток в проводнике может возникнуть только под действием сторонних сил, т.е. при наличии э.д.с.. В случае индукционного тока э.д.с., соответствующая сторонним силам, называется электродвижущей силой электромагнитной индукции εi.
Дальнейшие исследования индукционного тока в проводящих контурах различной формы и размеров показали справедливость следующего закона Фарадея:
Э.д.с. электромагнитной индукции в контуре пропорциональна скорости изменения магнитного потока Фm сквозь поверхность, ограниченную этим контуром:
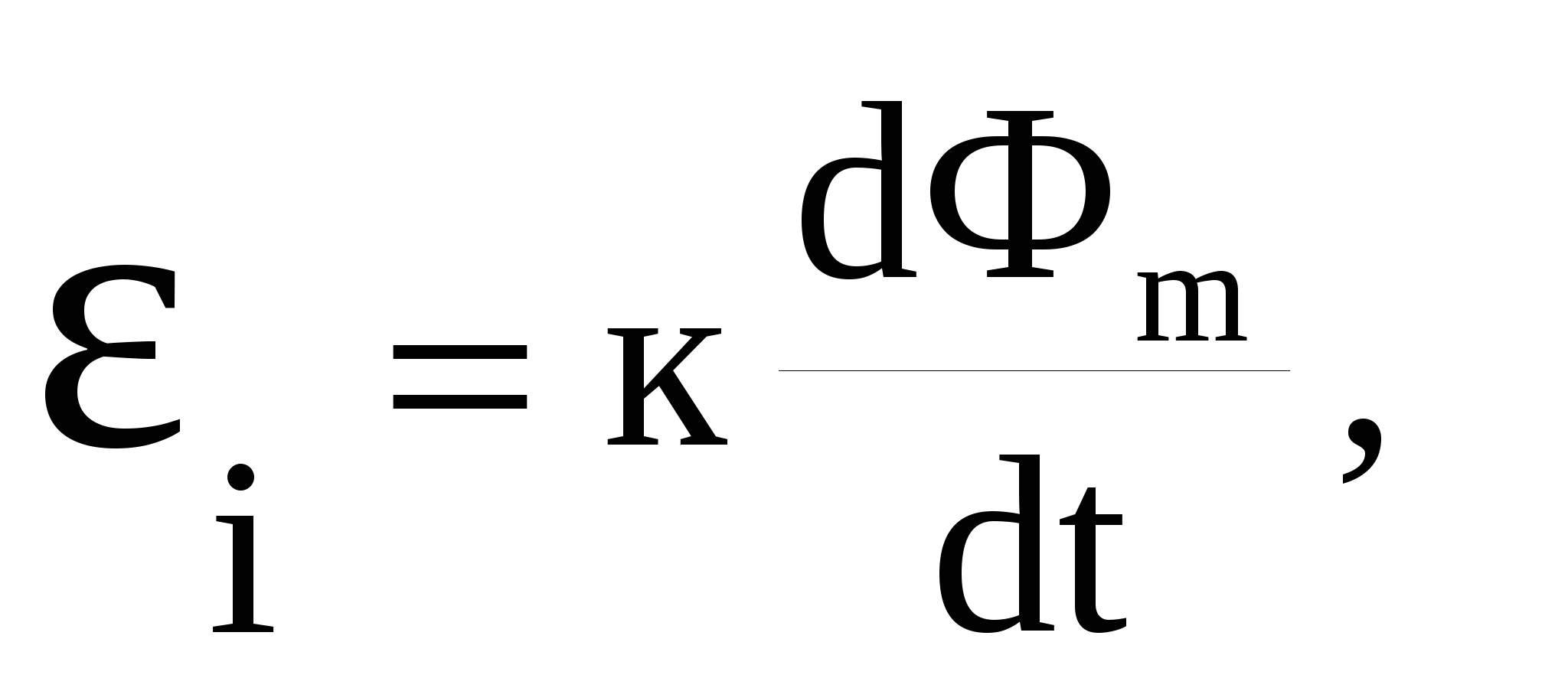
где к – коэффициент пропорциональности. Данная э.д.с. не зависит от того, чем вызвано изменение магнитного потока – либо перемещением контура в постоянном магнитном поле, либо изменением самого поля.
Рассмотрим пример, демонстрирующий данный закон (рис. 3.2). В контуре 1 создается ток силы I1, его можно изменять с помощью реостата R. Этот ток создает магнитное поле, пронизывающее контур 2. Если мы будем увеличивать ток I1, поток Фm магнитной индукции через контур 2 будет, изменяясь, расти. Это приведет к появлению в контуре 2 индукционного тока I2’, регистрируемого гальванометром G и направленного противоположно I1. Если, наоборот, уменьшать I1, то и поток через контур 2 будет уменьшаться, что приведет к появлению в нем индукционного тока I2’’, направленного так же, как I1.
К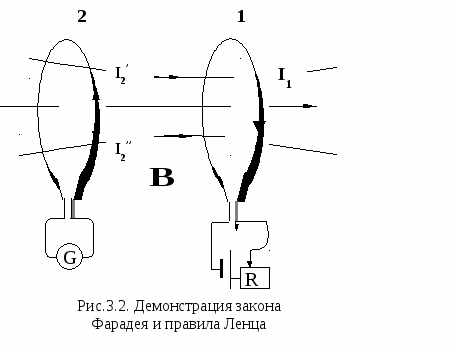 ак определить направление индукционного тока? Профессор Петербургского университета Э.Х.Ленц в 1833 г. установил, что индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Это – существенный физический факт, демонстрирующий стремление системы сопротивляться изменению состояния. ак определить направление индукционного тока? Профессор Петербургского университета Э.Х.Ленц в 1833 г. установил, что индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Это – существенный физический факт, демонстрирующий стремление системы сопротивляться изменению состояния.
Вернемся к рис. 3.2. При увеличении тока I1, т.е. возрастании потока магнитной индукции Фm, направленного вправо, когда dФm/dt >0, в контуре 2 возникает индукционный ток I2’, создающий собственный магнитный поток, направленный влево (данный поток стремится уменьшить Фm). Току I2’ соответствует εi< 0. Мы можем определить направление тока I2’ по правилу правого винта. Если ток в контуре 1 уменьшать, то dФm/dt < 0, и аналогично в контуре 2 возникает εi> 0 и ток I2”, собственный магнитный поток которого направлен так же, как и внешний поток Фm, потому что он стремится поддержать внешний поток постоянным, добавляя его.
Итак, направление индукционного тока определяется правилом Ленца: При всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.
Обобщением закона Фарадея и правила Ленца является закон Фарадея - Ленца: Электродвижущая сила электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:
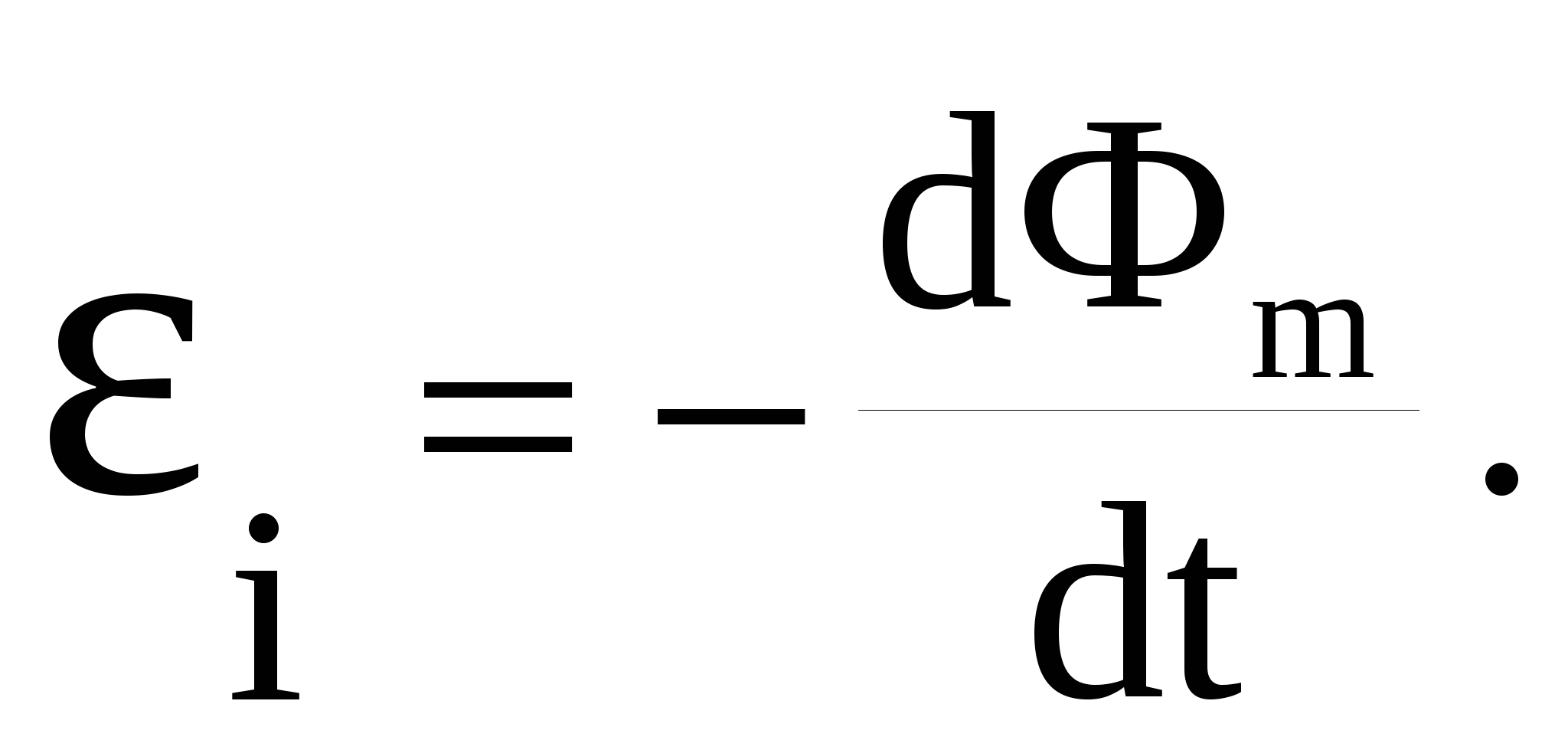
Это выражение представляет собой основной закон электромагнитной индукции.
При скорости изменения магнитного потока 1Вб/с в контуре индуцируется э.д.с. в 1 В.
Пусть контур, в котором индуцируется э.д.с., состоит не из одного, а из N витков, например, представляет собой соленоид. Соленоид – это цилиндрическая катушка с током, состоящая из большого числа витков. Так как витки в соленоиде соединяются последовательно, εi в данном случае будет равна сумме э.д.с., индуцируемых в каждом из витков по отдельности:
В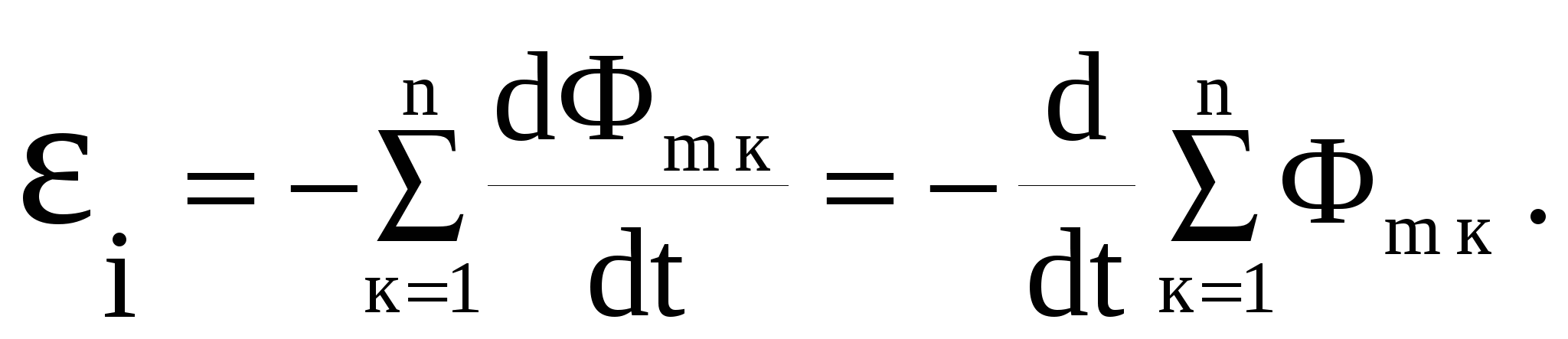
еличину Ψ = ΣΦm называют потокосцеплением или полным магнитным потоком. Если поток, пронизывающий каждый из витков, одинаков (т.е. Ψ = NΦm), то в этом случае
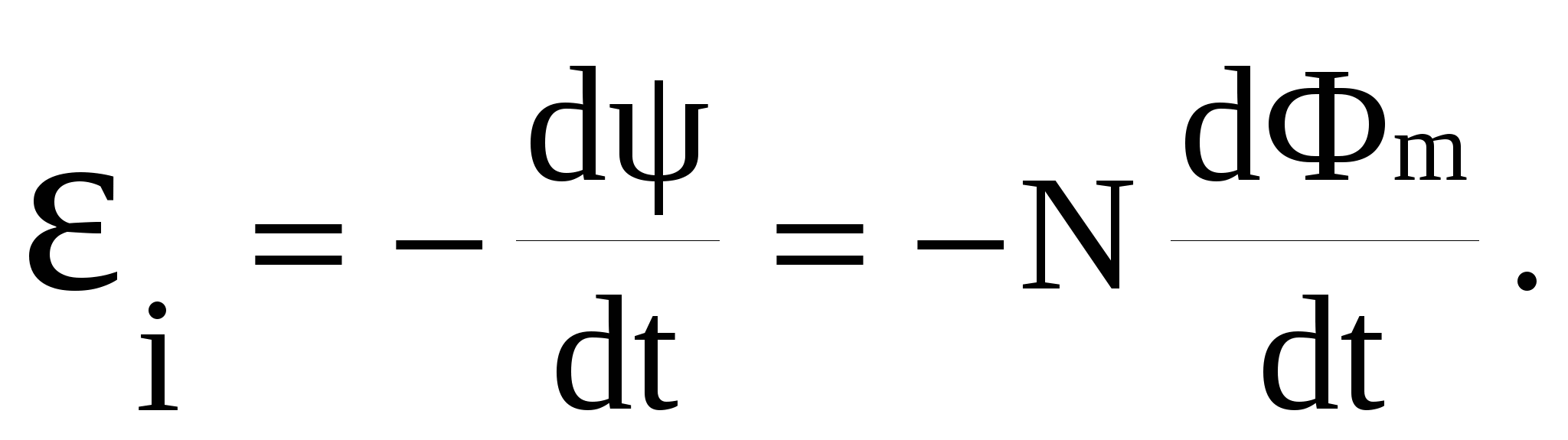
Немецкий физик Г.Гельмгольц доказал, что закон Фарадея-Ленца является следствием закона сохранения энергии. Пусть замкнутый проводящий контур находится в неоднородном магнитном поле. Если в контуре течет ток I, то под действием сил Ампера незакрепленный контур придет в движение. Элементарная работа dA, совершаемая при перемещении контура за время dt, будет составлять
dA = IdФm,
где dФm – изменение магнитного потока сквозь площадь контура за время dt. Работа тока за время dt по преодолению электрического сопротивления R цепи равна I2Rdt. Полная работа источника тока за это время равна εIdt. По закону сохранения энергии работа источника тока затрачивается на две названные работы, т.е.
εIdt = IdФm + I2Rdt.
Разделив обе части равенства на Idt, получим
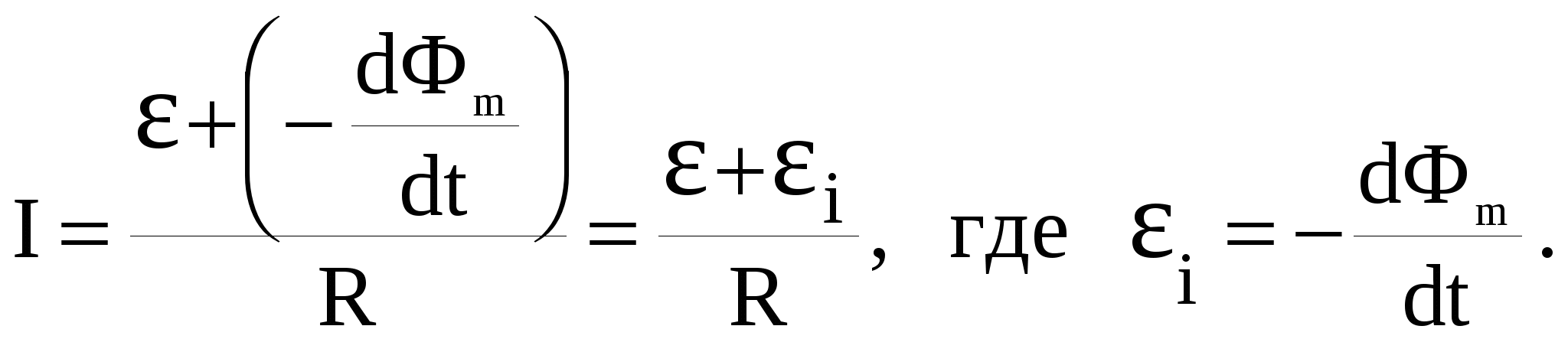
Следовательно, при изменении магнитного потока, сцепленного с контуром, в последнем возникает электродвижущая сила индукции 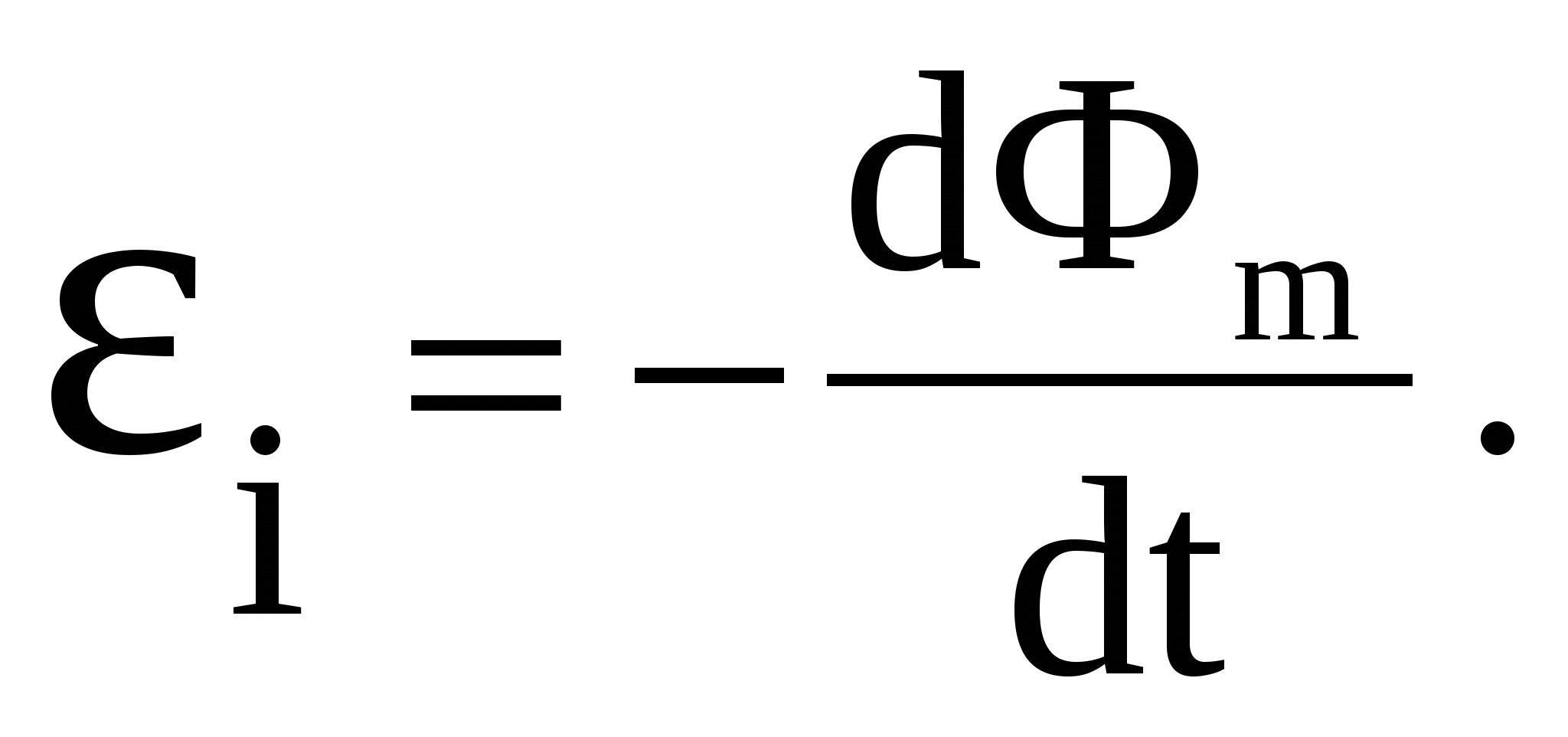
|
|
|
 Скачать 1.01 Mb.
Скачать 1.01 Mb.
 .1. Основной закон электромагнитной индукции.
.1. Основной закон электромагнитной индукции. 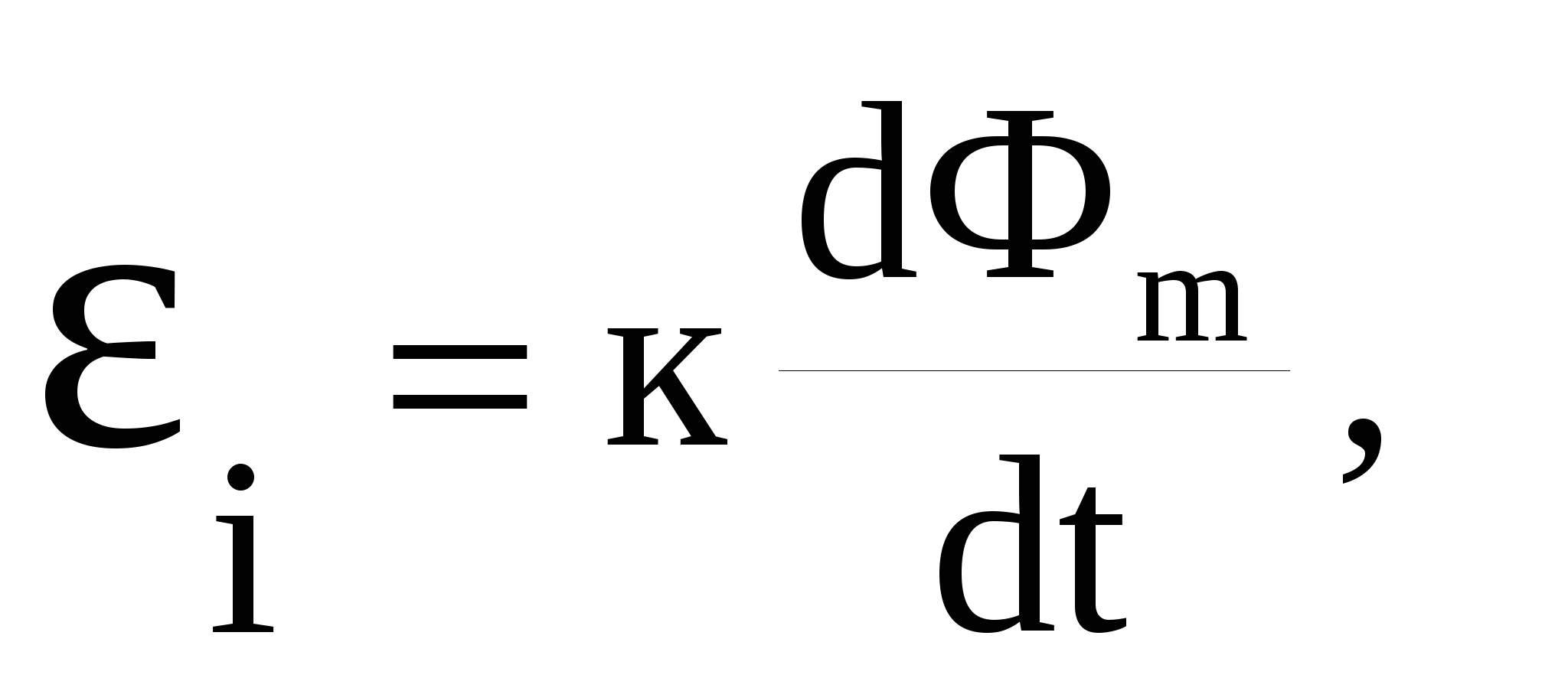
 ак определить направление индукционного тока? Профессор Петербургского университета Э.Х.Ленц в 1833 г. установил, что индукционный ток всегда направлен так,
ак определить направление индукционного тока? Профессор Петербургского университета Э.Х.Ленц в 1833 г. установил, что индукционный ток всегда направлен так,