Учебник по физике магнетизма. Учебник по физике кгтукхти. Кафедра физики. Старостина И. А., Кондратьева О. И., Бурдова Е. В. Для перемещения по тексту электронного учебника можно использовать
 Скачать 1.01 Mb.
|
3.4. Энергия магнитного поля. @Д 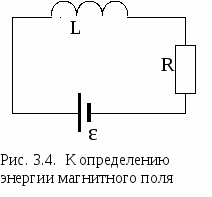 ля определения энергии магнитного поля рассмотрим контур, состоящий из источника э.д.с. - ε, катушки индуктивности - L и сопротивления - R (рис.3.4). При замыкании цепи ток возрастает от 0 до I, и, следовательно, возникает э.д.с. самоиндукции εis, направленная против э.д.с. ε, возбуждающей ток. При размыкании цепи сила тока уменьшается от I до 0, что вызывает появление э.д.с. самоиндукции εis того же направления, что и направление внешней ε. Можно предположить, что на увеличение тока в контуре затрачивается дополнительная работа, идущая на создание энергии магнитного поля. При снижении тока эта энергия выделяется в виде дополнительного джоуль-ленцева тепла.Пусть при замыкании контура ток меняется со скоростью dI/dt. Тогда, как мы уже знаем, в контуре индуцируется э.д.с. самоиндукции εs, равная -LdI/dt, препятствующая изменениям тока. В контуре действует также постоянная э.д.с. ε. Если за положительное направление тока принять то направление, в котором ε заставляет течь ток в контуре, то полная э.д.с. в любой момент времени будет равна ε- LdI/dt. Эта суммарная э.д.с. вызывает ток I через сопротивление R. На сопротивлении происходит падение напряжения, равное IR. Закон Ома для контура имеет вид  .Подсчитаем работу, совершаемую источником э.д.с. за время dt. Для этого воспользуемся формулой для мощности тока N=dA/dt=Iε. Объединив два последних выражения, получим 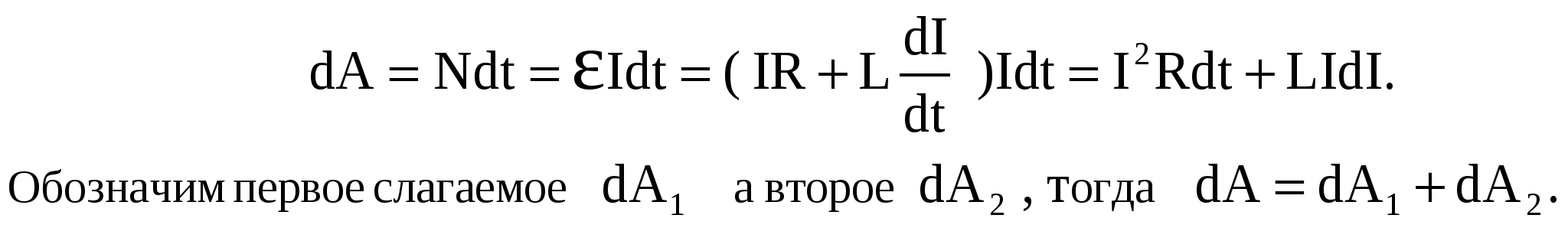 Первое слагаемое dA1 = I2Rdt – это работа, расходуемая на нагревание проводника, т.е. тепло, выделяемое в проводнике за время dt. Второе слагаемое dA2 = LIdI – работа, обусловленная индукционными явлениями. Данная дополнительная работа, затрачиваемая на увеличение силы тока в контуре от 0 до I, находится как интеграл:  .Полученная работа LI2/2 представляет собой собственную энергию тока в контуре с индуктивностью L. Увеличение силы тока в проводнике вызывает соответствующее усиление его магнитного поля, которое, подобно электрическому, обладает энергией. Найденная нами собственная энергия тока в контуре есть не что иное, как энергия Wm магнитного поля этого контура с током. Эта энергия запасена в магнитном поле катушки так же, как энергия электрического поля запасена в заряженном конденсаторе. Таким образом,  .В этой формуле магнитная энергия выражена через параметры, характеризующие контур с током – силу тока I и индуктивность катушки L. Ту же энергию Wm можно выразить через параметры, характеризующие само магнитное поле, а именно, напряженность поля  , магнитную индукцию  и объем занимаемого полем пространства V. Для этого найдем энергию магнитного поля соленоида. Воспользуемся полученным нами ранее выражением для индуктивности соленоида: L = n2μμ0V. Индукция магнтного поля соленоида В = nμμ0I, откуда I=B/nμμ0. Таким образом, искомая энергия: 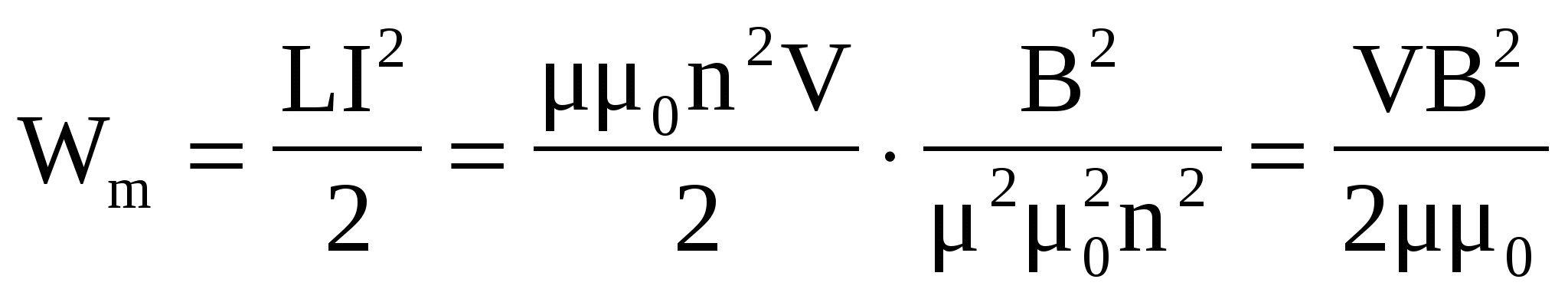 .Так как В= μμ0Н, то  . Если магнитное поле однородно, его энергия распределена равномерно по всему объему поля с некоторой объемной плотностью wm:  .Последнее соотношение можно переписать в трех эквивалентных формах:  .Если магнитное поле неоднородно, его объемная плотность меняется от точки к точке. Зная wm в каждой точке, можно найти энергию поля, заключенную в некотором объеме V. Для этого нужно вычислить интеграл:  .4. УРАВНЕНИЯ МАКСВЕЛЛА. @4.1. Теория Максвелла для электромагнитного поля. @В 60-х годах XIX столетия Д.К. Максвелл, ознакомившись с работами Фарадея, решил придать теории электричества и магнетизма математическую форму. Обобщив законы, установленные экспериментальным путем – закон полного тока, закон электромагнитной индукции и теорему Остроградского-Гаусса, - Максвелл дал полную картину электромагнитного поля. В теории Максвелла решается основная задача электродинамики – установление характеристик электромагнитного поля заданной системы электрических зарядов и токов, т.е. определение напряженности электрического поля Е и индукции магнитного поля В при известных величинах зарядов и токов, создающих эти поля. Необходимо отметить, что в своих выводах Максвелл не мог воспользоваться теорией относительности, так как она появилась лишь спустя 50 лет. Не были изучены электрические свойства веществ, не была установлена связь электромагнетизма и света. Другими словами, многие из доводов, которыми пользуемся мы сейчас при теоретическом обобщении результатов, были немыслимы во времена Максвелла. Данная теория явилась величайшим вкладом в развитие классической физики. Она позволила с единой точки зрения охватить огромный круг явлений, начиная от электростатического поля неподвижных зарядов и кончая электромагнитной природой света. В этой теории не рассматривается молекулярное строение среды и внутренний механизм процессов, происходящих в веществе, находящемся в электромагнитном поле. Теория Максвелла – макроскопическая, в ней рассматриваются электромагнитные поля таких зарядов и токов, пространственная протяженность которых неизмеримо больше размеров атомов и молекул. Электрические и магнитные свойства среды в теории Максвелла характеризуются тремя величинами: относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью μ и удельной электрической проводимостью γ. Предполагается, что эти параметры среды известны из опыта. Данная теория представлена в виде системы четырех уравнений, называемых уравнениями Максвелла. Эти уравнения принято записывать в дифференциальной и интегральной форме. Уравнения в дифференциальной форме показывают, как связаны между собой характеристики электромагнитного поля и плотности электрических зарядов и токов в каждой точке этого поля. В данном разделе рассмотрены только уравнения Максвелла в интегральной форме – они содержат соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей. |