Статистический анализ учебника иностранного языка (1). Учебника иностранного языка дисциплина Учебная практика, практика по применению математической статистики в исследованиях

• Название: Учебника иностранного языка дисциплина Учебная практика, практика по применению математической статистики в исследованиях
• Дата: 14.05.2023
• Размер: 328.66 Kb.
• Имя файла: Статистический анализ учебника иностранного языка (1).docx
• Тип: Учебник; #1127855
• страница: 2 из 4

3. Составить для каждого УМК вариационные ряды распределения слов в каждом тексте.

Для составления вариационных рядов нужно выделить два признака: Х и N, где Х – это количество слов, а N- частота (т.е. сколько раз было такое количество слов).

Пусть для изучения количественного (дискретного или непрерывного) признака X из
генеральной совокупности извлечена выборка x1 , x2 ,..., xk объема n. Наблюдаемые
значения xi признака X называются вариантами. Последовательность вариант, записанных в возрастающем порядке, называют вариационным рядом

В нашем случае x_1.1 - 13 (минимальное количество слов в тексте из УМК 1), а x₁.₁₀ - 21(максимальное количество слов в тексте УМК 1). В таблице ниже необходимо записать количество слов от минимального до максимального.

Числаn1 , n2 ,..., nk называются частотами. Таблица, отображающая зависимость между вариантами xi и частотами ni называется вариационным рядом.
Общий формат вариационного ряда: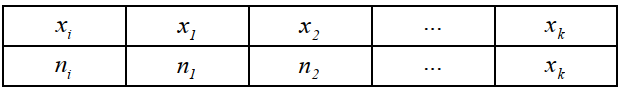



Важно! Если одно и тоже количество слов оказывается в нескольких текстах, то количество слов по признаку Х указываем один раз, а в признаке N указываем сколько раз встретилось такое количество. В нашем случае, 13 слов встретилось в 2х текстах, 17 слов в 3 и т.д.

Пример для УМК 1

Мы пишем: Вариационный ряд для УМК Enjoy English 3

x1.i	x1.1	x1.2	x1.3	x1.4	x1.5
n1i	n1.1	n1.2	n1.3	n1.4	n1.5

x1i	13	16	17	20	21
n1i	2	1	3	2	2

Пример для УМК 2

Мы пишем: Вариационный ряд для УМК Enjoy English 8

x2i	x2.1	x2.2	x2.3	x2.4	x2.5	x2.6
n2i	n2.1	n2.2	n2.3	n2.4	n2.5	n2.6

x2i	13	15	16	17	21	24
n2i	1	1	2	2	1	3

ЧАСТЬ 3.1.

4. 
   Осуществить расчет статистических характеристик для каждого из вариационных рядов.
   Вариационные ряды для каждого из текстов представлены выше.
   1. Объем выборки вариационного ряда обозначается как n и равняется сумме
   частот n_i для каждого из вариантов x_i: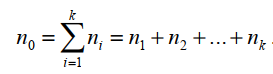
   

где k – количество показателей в таблице вариационных рядов. В нашем случае УМК 1 – 5, а УМК 2 – 6;

n – частоты, их значения берем из таблицы вариационных радов (см.выше).
Пример для УМК 1 (Мы пишем: Расчет объема выборки для УМК Enjoy English 3)



n₁₀_n_1in_1,1n_1,2...n_1,52132210.

i1


6

ПримердляУМК2:

n₂₀ _n_2i n_2,1 n_2,2 ...n_2,6 11221310.

i1


Характеристики выборочного среднего значения


2. Выборочная средняя вариационного ряда или выборки объемом nобозначается x и равняется отношению суммы произведений вариантов xi на их частоты ni к объему выборки n: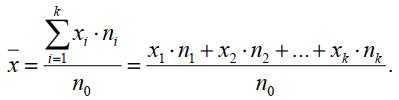



где n₀– объем выборки. В нашем случае 10 (см.выше)

значения x_iи n_{i –} значения из таблицы вариационных рядов.
Пример для УМК 1 (Мы пишем: Выборочная средняя для УМК Enjoy English 3)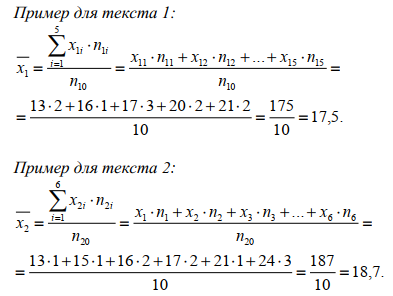




Пример для УМК 2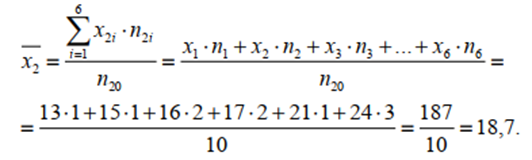


3. Выборочная медиана вариационного ряда или выборки объемом n обозначается 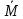_Ex и равняется значению варианта вариационного ряда, для которого одновременно выполняются два неравенства с точки зрения распределения частот слева и справа, включая рассматриваемое значение: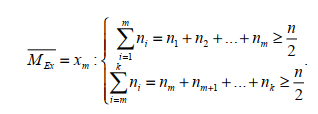


где, x_m- это текст с центральным значением, которое делит ряд на одинаковые части. В нашем случае, в УМК 1 x_{1.3 =}17. Для УМК 2 нужно взять 2 центральных значений x_2.6 и x_2.7 (16+17)и делим на 2, округляем в большую сторону.

n₁–значения частот до центрального

n_m – значения частот после центрального значения.

n–объем выборки (см.выше).

Пример для УМК 1(Мы пишем: Выборочная медиана для УМК Enjoy English 3)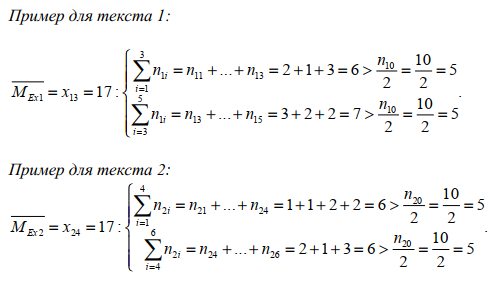




П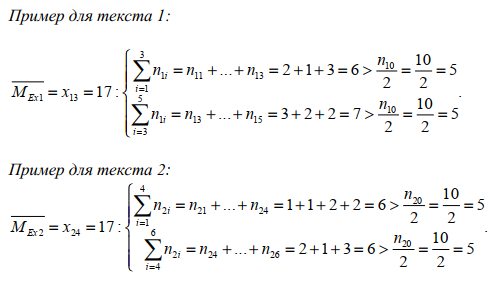
ример для УМК 2
Характеристики отклонения от выборочного среднего значения

4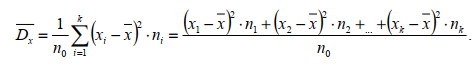
. Выборочная дисперсия вариационного ряда или выборки объемом n обозначается 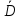_x и равняется отношению суммы произведений квадратов разностей
между значениями вариантов и средней выборочной величины на их частоты к объему
выборки:

где, n0 – объём выборки. В нашем случае 10 (см.выше);

k – количество показателей в таблице вариационных рядов. В нашем случае УМК 1 – 5, а УМК 2 – 6;

x₁–значения вариантов из таблицы вариационных рядов 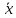(см.выше);

– выборочная средняя ( см.выше)

n₁ – объем выборки (см.выше)
Пример для УМК 1(Мы пишем: Выборочная дисперсия для УМК Enjoy English 3)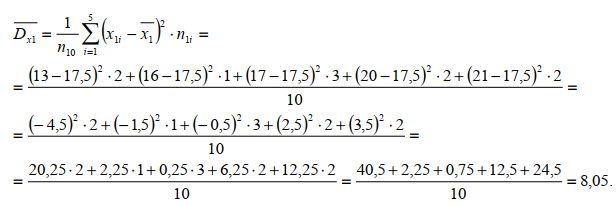

Пример для УМК 2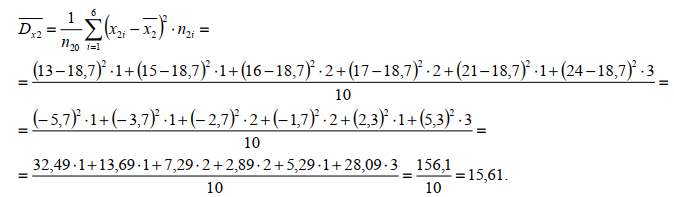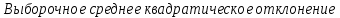

1. 
   вариационного ряда или
   выборки объемом n обозначается 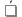_x и равняется квадратному корню из выборочной
   дисперсии вариационного ряда или выборки объемом n: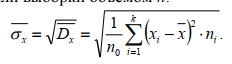
   

где, 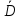_x– выборочная дисперсия (см.выше).

Пример для УМК 1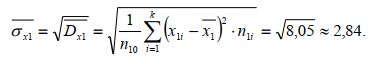



Пример для УМК 2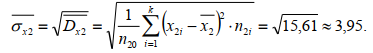


5. Осуществить сравнительный анализ имеющихся вариационных рядов на выявление взаимосвязей между текстами.



Коэффициенты корреляции
Выборочный коэффициент корреляции Пирсона


На основании исходных данных исходных вариационных рядов составляем ковариационную матрицу:

X1 X2	x2.1	x2.2	…	x2m	n1i
x1.1	n(x1.1,x2.1)	n(x1.1,x2.2)	…	n(x1.1,x2m)	n1.1
x1.2	n(x1.2,x2.1)	n(x1.2,x2.2)	…	n(x1.2,x2m)	n1.1
…	…	…	…	…	…
x1.k	n(x1.k,x2.1)	n(x1k,x2.2 )	…	n(x1k,x2m)	n1k
n2.i	n2.1	n2.2	…	n2m	n10n20

Пример ковариационной матрицы для УМК 1 и 2:

X1X2	x2.1	x2.2	x2.3	x2.4	x2.5	x2.6	n1i
x1.1	n(x1.1,x2.1)	n(x1.1,x2.2)	n(x1.1,x2.3 )	n(x1.1,x2.4)	n(x1.1,x2.5)	n(x1.1,x2.6)	n1.1
x1.2	n(x1.2,x2.1)	n(x1.2,x2.2)	n(x1.2,x2.3 )	n(x1.2,x2.4)	n(x1.2,x2.5)	n(x1.2,x2.6)	n1.2
x1.3	n(x1.3,x2.1)	n(x1.3,x2.2)	n(x1.3,x2.3)	n(x1.3,x2.4)	n(x1.3,x2.5 )	n(x1.3,x2.6)	n1.3
x1.4	n(x1.4,x2.1)	n(x1.4,x2.2)	n(x1.4,x2.3 )	n(x1.4,x2.4)	n(x1.4,x2.5)	n(x1.4,x2.6)	n1.4
x1.5	n(x1.5,x2.1)	n(x1.5,x2.2)	n(x1.5,x2.3)	n(x1.5,x2.4)	n(x1.5,x2.5)	n(x1.5,x2.6)	n1.5
n2i	n2.1	n2.2	n2.3	n2.4	n2.5	n2.6	n10n20

X1 X2	13	15	16	17	21	24	n1i
13	1	1	0	0	0	0	2
16	0	0	1	0	0	0	1
17	0	0	0	1	1	1	3
20	0	0	0	1	0	1	2
21	0	0	1	0	0	1	2
n2i	1	1	2	2	1	3	10 = 10

Числовые характеристики совокупности вариационных рядов


1. Выборочная ковариация совокупности вариационных рядов обозначается k(X1, X 2 ) и равняется отношению суммы произведений разностей между значениями вариантов и средней выборочной величины для каждой из исходных выборок на частоты совместного появления данных значений к объему равных выборок исходных вариационных рядов: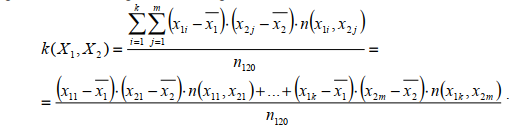



где, x₁ – значения вариантов из таблицы вариационных рядов 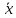(см.выше);

– выборочная средняя ( см.выше)

n – показатель из ковариационной матрицы (см.выше). В нашем случае, 1 или 0.


Пример выборочной корреляции для УМК 1 и 2

X1 X2	13	15	16	17	21	24	n1i
13	25,65	16,65	0	0	0	0	42,3
16	0	0	4,05	0	0	0	4,05
17	0	0	0	0,85	-1,15	-2,65	-2,95
20	0	0	0	-4,25	0	13,25	9
21	0	0	1	-9,45	0	18,55	9,1
n2i	25,65	16,65	-5,4	-3,4	-1,15	29,15	61,5 = 61,5

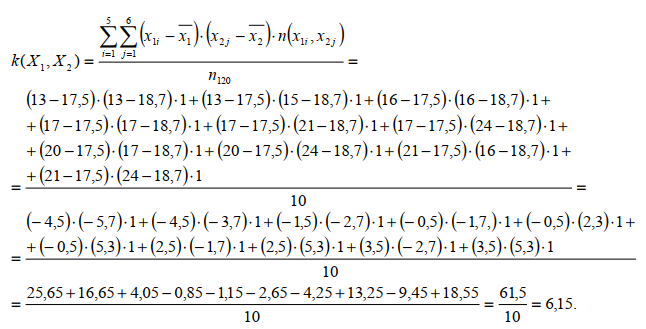2. Коэффициент корреляции Пирсона совокупности вариационных рядов
обозначается r(X1,X2) и равняется отношению выборочной ковариации к
произведению выборочных средних квадратических отклонений исходных
вариационных рядов: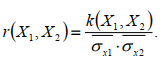



где,k(X1,X2) – выборочная ковариация 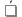( см.выше);

_x- выборочное среднее квадратическое отклонение (см. выше).
Пример коэффициента корреляции для УМК 1 и 2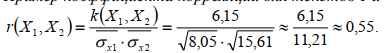




Значение коэффициента корреляции Пирсона отражает степень связи с точки зрения совокупностей значений и частотами их совместного появления для совокупностей вариационных рядов X1 и X 2 с одинаковым объемом выборки:
 Если значение коэффициента корреляции равно 0, то вариационные ряды X1 и
X 2 с одинаковым объемом выборки никак не связаны друг с другом с точки зрения
значений, то есть являются некоррелированными.
 Если значение коэффициента корреляции отлично равно 1, то между
вариационными рядами с одинаковым объемом выборки X1 и X 2 существует строго
прямая связь, тогда как при значении -1 наблюдается строго обратная связь.
 Если значение коэффициента корреляции отлично от 0, то вариационные ряды X1
иX 2 с одинаковым объемом выборки никак связаны друг с другом с точки зрения
значений, то есть коррелируют друг с другом с определенным характером и силой связи.
 Если значение коэффициента корреляции отлично от 0 и является отрицательным
числом ( 1rX1, X 2 0 ), то существует обратная по характеру связь между
вариационными рядами с одинаковым объемом выборки X1 и X 2 связь, тогда как в
обратном случае ( 0 rX1, X 21) связь является прямой по характеру.

Сила связи выбирается по таблице: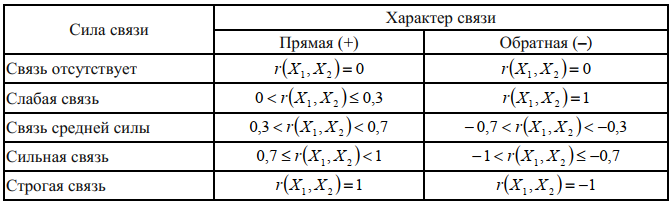



Пример коэффициента корреляции для УМК 1 и 2:
rX1, X 2  0,55.
Так какrX1, X 2 0, то связь между объёмом текстов и этапом обучения (УМК 1 и 2) по характеру связи является прямой.
Так как 0,3 rX1, X 2 0,7 , то связь между распределением по силе связи является средней.

Вывод: существует прямая связь между обьемом текстов и этапом обучения, но данная связи средняя по силе.
ЧАСТЬ 3.2