Урок математики в 11 классе. Урок математики 11 класс. Учебнику Алгебра и начала математического анализа авторы С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. Тема урока Равносильные преобразования уравнений Тип урока урок систематизации и обобщения знаний Цели урока
 Скачать 0.55 Mb.
|
|
11 класс по учебнику Алгебра и начала математического анализа авторы С.М.Никольский, М.К.Потапов, Н.Н. Решетников, А.В.Шевкин. Тема урока: «Равносильные преобразования уравнений» Тип урока: урок систематизации и обобщения знаний Цели урока: - формировать навыки равносильных переходов при решении уравнений; - создавать условия для закрепления, повторения и углубления знаний. Задачи урока: Образовательная: рассмотреть примеры равносильных переходов при решении уравнений; закрепить умение применять основные теоремы равносильности при решении уравнений; способствовать расширению знаний по изучаемой теме; Развивающие: развитие логического мышления, познавательного интереса; формирование математической речи, умения анализировать и сравнивать, делать выводы; развитие приемов умственной деятельности, умения искать рациональный способ решения поставленной задачи; повышение информационной культуры учащихся, интереса к предмету; развитие потребности к самообразованию, умение вырабатывать собственную позицию (обосновывать свой решения, свой результат); воспитательные: обучение эстетическому оформлению записи в тетради и на доске, воспитание ответственности, самостоятельности, умения работать в коллективе; Планируемые результаты: Личностные: - умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи; выстраивать аргументацию - критичность мышления; - креативность мышления, активность при решении математических задач; - умение контролировать процесс и результат учебной деятельности; Метапредметные: - умение видеть математическую задачу в контексте проблемной ситуации; -умение понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации; - умение видеть различные стратегии решения задач; Предметные: - умение определить значение идеи, методов и результатов алгебры для построения модели реальных процессов и ситуаций; Ход урока 1)Организационный момент. Самоопределение. Приветствие учащихся, проверка готовности к уроку, вступительное слово учителя, запись в тетрадях числа. Приобретать знания – храбрость, Приумножать их – мудрость, А умело применять – великое искусство. 2) Постановка цели и задач урока. Ребята, я предлагаю сегодня на уроке привести в систему знания и расширить представление о равносильности уравнений. Я уверена, что у вас есть желание узнать новое, анализировать, делать выводы, найти свой путь решения и расширить знания, которые вам понадобятся для успешной сдачи ЕГЭ. Решение уравнений является основной темой, которая входит в ЕГЭ в базовый и профильный уровни. 3)Актуализация опорных знаний и фиксирование затруднений. Скажите, что мы изучили с вами на предыдущем уроке? Какие уравнения называются равносильными? Какие преобразования уравнения называют равносильными? Объясните, почему равносильны уравнения? № 7.3 (в,г,ж) 4)Применение знаний и умений. Работа с учебником: №7.7(а,в), №7.8(в), №7.9(б,е) (пять учащихся решают у доски, пять учащихся работают с каждым в паре) Решите уравнения (задания из откр.банка базовый ур) (1,2,3-1вариант, 4,5,6-2вариант) 1)  , 2) 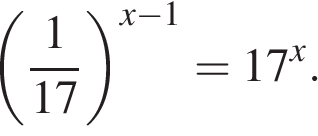 3)  , 4)  , 5)  ,6)  Работа в парах: ( за доской записаны ответы, учащиеся обмениваясь тетрадями, проверяют решение уравнений и оценивают своего соседа по парте) Физминутка. (Упражнения для глаз с использованием геометрических фигур, расположенных на стене классной комнаты, это квадрат, круг, треугольник, трапеция. Во время физкультминутки дается задание последовательно перемещать взгляд с одной фигуры на другую по названию фигуры(цвета) учителем.) Работа в роли экспертов: ( Учащиеся на листах проверяют решение тригонометрического уравнения и комментируют правильность решения уравнения, те , кто сдают ЕГЭ профиль выставляют баллы) 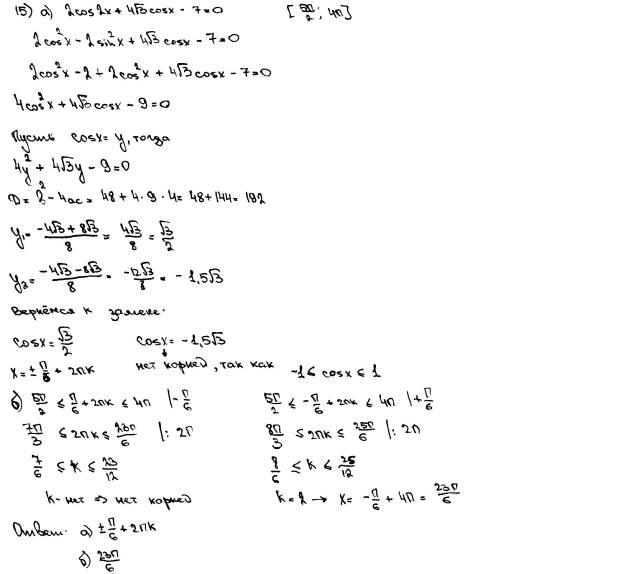 Комментарий. Нигде в решении нет описания значений параметра k, но при отборе корней явно указано целое значение. Считаем, что выставление наивысшего балла возможно. Оценка эксперта: 2 балла. 5)Домашнее задание. П.7.1, №7.4(б,г), №7.5(б,г), №7.10(в,г) (задание записано на слайде презентации) Подготовка к ЕГЭ (приложение) 6) Рефлексия. Подведение итогов. Выставляются оценки за урок. Учащиеся вместе с учителем подводят итог урока Сегодняшний урок – это …… Сегодня на уроке я - ……… Приложение Базовый уровень 1. Найдите корень уравнения  2. Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.3. Найдите корень уравнения  .4. Найдите корень уравнения  .5. Найдите корень уравнения:  Если уравнение имеет более одного корня, укажите меньший из них.6. Найдите корень уравнения:  7. Решите уравнение:  8. Найдите корень уравнения  9. Решите уравнение  .10. Найдите решение уравнения: 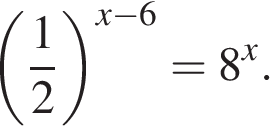 11. Найдите корни уравнения:  В ответ запишите наибольший отрицательный корень.12. Решите уравнение  . В ответе напишите наибольший отрицательный корень.Профильный уровень 1. а) Решите уравнение  б) Укажите корни этого уравнения, принадлежащие отрезку  2. а) Решите уравнение  б) Укажите корни этого уравнения, принадлежащие отрезку  4.Изучение и закрепление материала 1. Теоремы о равносильности уравнений В основном при решении уравнений используются шесть Теорем равносильности. Первые три теоремы Безусловные. Они гарантируют равносильность преобразований без дополнительных условий. Их применение обычно происходит автоматически, без особых размышлений. Теорема 1. Если любой член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному. Например, уравнения У]2х + \ - 2х + 5 = 0 и V2x + 1 = 2х - 5 равносильны. Теорема 2. Если обе части уравнения возвести в одну и ту же НеЧетную Степень, то получится уравнение, равносильное данному. Например, уравнения л/Зх + 2 = х И 3x + 2 = xJ равносильны. Теорема 3. Показательное уравнение Af^X' = A^X' (где A > О, А Ф 1) равносильно уравнению Fix) = G(X). Например, показательное уравнение з =32дг"5 равносильно иррациональному уравнению Теорема 4. Если обе части уравнения Fix) = G(X) Умножить на одно и то же выражение H(X\ Которое: А) имеет смысл в области определения уравнения Fix) = G(X); Б) нигде в этой области не обращается в нуль, То получится уравнение Fix)H(X) = G(X)H(X), Равносильное данному. Теорема 5. Если обе части уравнения Дх) = g(x) неотрицательны в области определения уравнения, то после возведения обеих его частей в одну и ту же четную степень П Получится уравнение, равносильное данному: F"(X) = G"(X). Теорема 6. Если Fix) > 0 и G(X) > О, то логарифмическое уравнение loga F{X) = Loga g(x) (где A > 0, A Ф 1) равносильно уравнению Преобразования приводящие к равносильному уравнению 1. Перенос членов уравнения из одной части в другую с противоположными знаками 2. Умножение или деление обеих частей уравнения на одно и то же число, отличное от нуля, или на выражение, имеющее постоянный знак при всех значениях неизвестного 3. Замена части уравнения тождественно равным ему выражением 4. Возведение уравнения в нечетную степень 5. Извлечения корня нечтной степени из обеих частей уравнения 6 Логарифмирование показательного уравнения Работа по учебнику - № 7.4 (а,в) , 7.5 (а,в) , 7.6 (а,в) , (У доски решает один из учащихся) 5) Рефлексия. Подведение итогов урока Понятно, что, кроме равносильных преобразований неравенств, есть и неравносильные, от которых, решая неравенства, нужно держаться подальше. А дело здесь в том, что, выполнив переход к неравносильному неравенству, можно получить решение, которое не является искомым решением исходного неравенства. В некоторых случаях можно получить и верный ответ, но это будет не более чем везение, а в общем случае, выполняя неравносильные преобразования неравенств, будет получен неверный ответ. Вывод ясен: при решении неравенств нужно выполнять только равносильные преобразования. При обобщении изученного материала обучающие отвечают на вопросы: Что нового было на уроке? Больше всего затруднений вызвало… Для меня непонятно было… 6) Домашнее задание По учебнику решить - № 7.4 (б,г) , 7.5 (б,г) , 7.6 (б,г)) П.7.1 учить 11 класс по учебнику Алгебра и начала математического анализа авторы С.М.Никольский, М.К.Потапов, Н.Н. Решетников, А.В.Шевкин. |