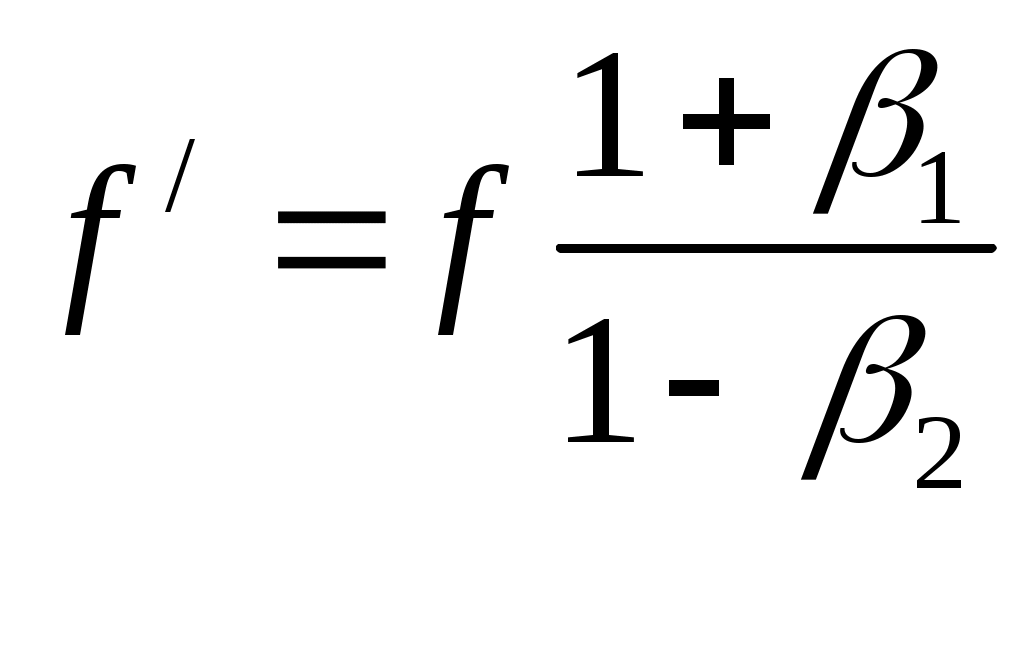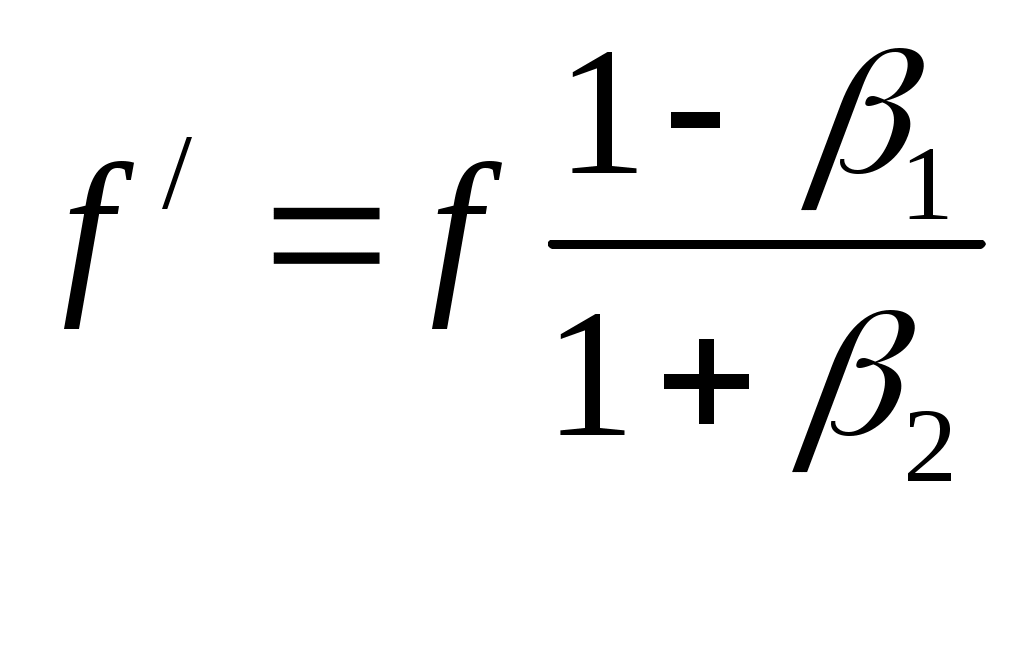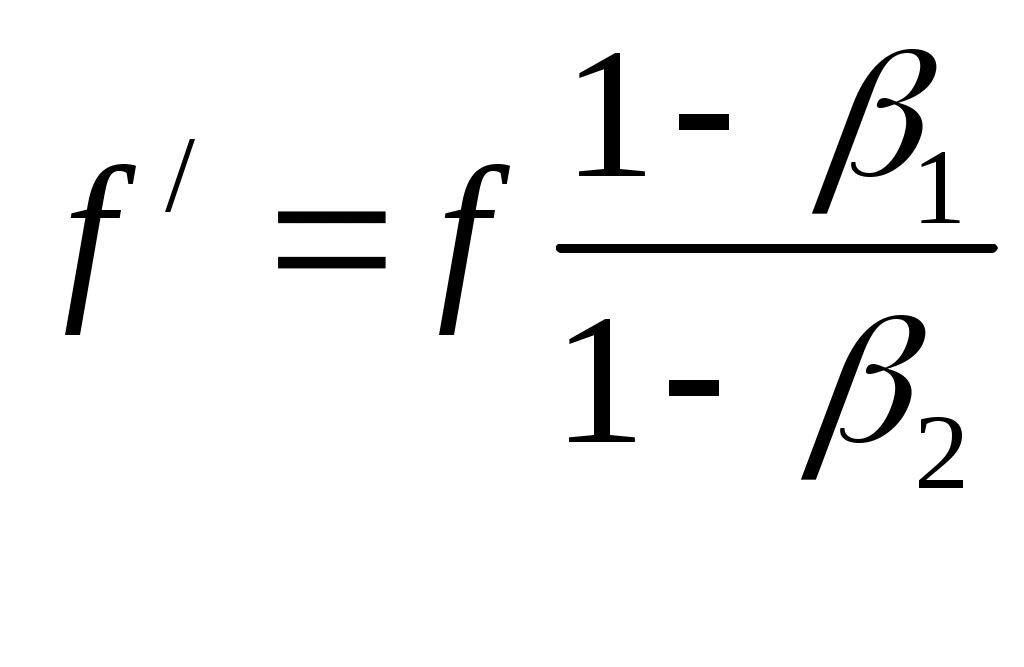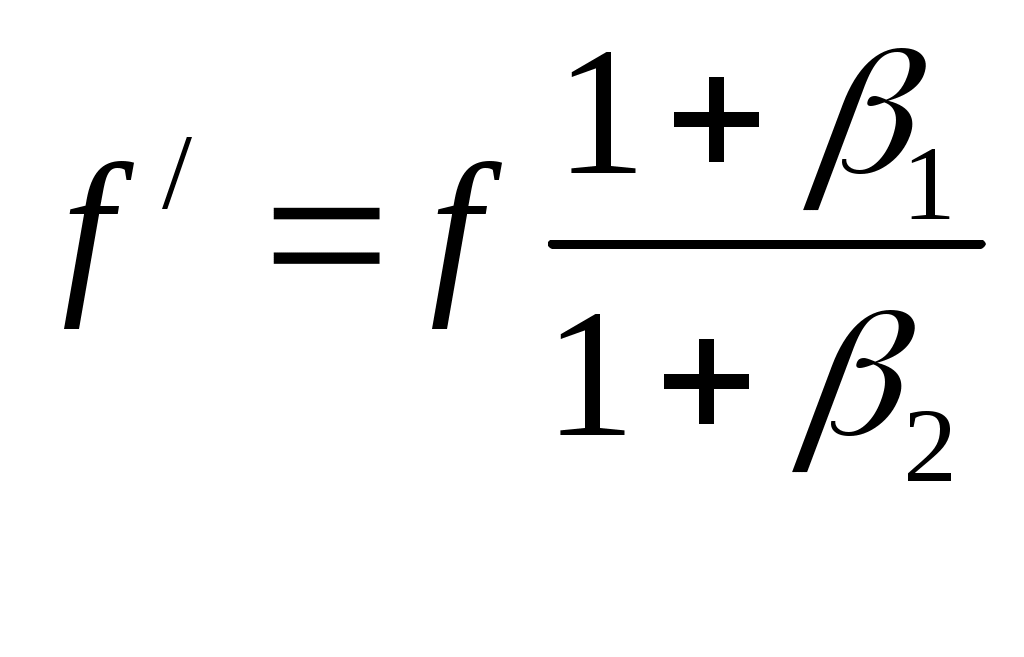Учебнометодический комплекс для заочного обучения с применением дистанционных технологий для студентов специальности 190702 Организация и безопасность дорожного движения
 Скачать 5.75 Mb. Скачать 5.75 Mb.
|
Эффект ДоплераПражский профессор Христиан Доплер(1803 – 1853) в 1842г. опубликовал статью «Об окрашенном свете двойных звезд и некоторых других небесных светил», где впервые рассмотрел вопрос об изменении частоты излучения света в зависимости от движения его источника или приемника. Предсказанный им эффект относится к колебаниям любой природы, так что его механизм действия можно проиллюстрировать на примере расходящихся кругов по поверхности воды от периодически погружаемого в воду поплавка i. Если поплавок i покоится, то на водной глади образуется ряд вложенных колец различного диаметра, имеющих общий центр (рис. 10.11а); если поплавок i равномерно и прямолинейно перемещается, продолжая совершать колебания, то центры окружностей сместятся вдоль оси x (рис. 10.11б). 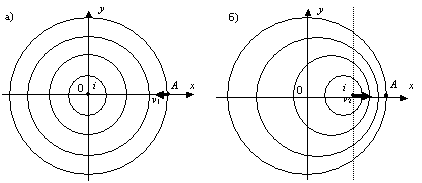 Рисунок 10.11 Эффект Доплера источник колебаний i покоится, приемник A движется со скоростью v1 по направлению к источнику (а); приемник A покоится, источник i движется со скоростью v2 по направлению к приемнику (б). В обоих случаях будет наблюдаться изменение длины волны λ. Обозначим параметры собственных колебаний поплавка следующими буквами: f – частота колебаний, T – период, λ – длина волны, а через c – скорость распространения волны по поверхности воды. Тогда для неподвижного источника и покоящегося наблюдателя будут справедливы следующие соотношения: λ = cT, λ = c/f, T = 1/f. Теперь вообразите, что поплавок i никуда не перемещается, а вы в роли наблюдателя (или приемника A) плывете на лодке со скоростью v1< c вдоль оси x по направлению к источнику колебаний i (рис. 9.1а). Понятно, что длина волны λ для вас уменьшится и станет равной λ1. Так как вы плывете навстречу волне, набегающей на вас, то относительная скорость окажется равной сумме скоростей: c + v1. Очевидно, что длина волны λ1 во столько раз меньше длины волны λ, во сколько раз c меньше c + v1, т.е. 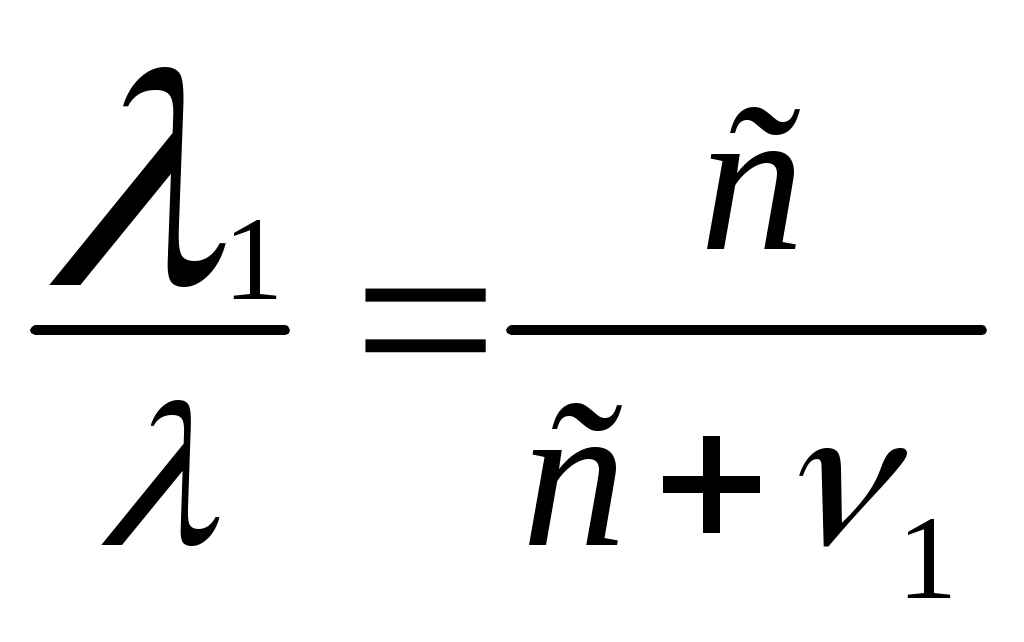 , (10.1) , (10.1)Период колебаний T для вас также сократится и будет равным T1, а частота f, напротив, увеличится и станет равной f1: 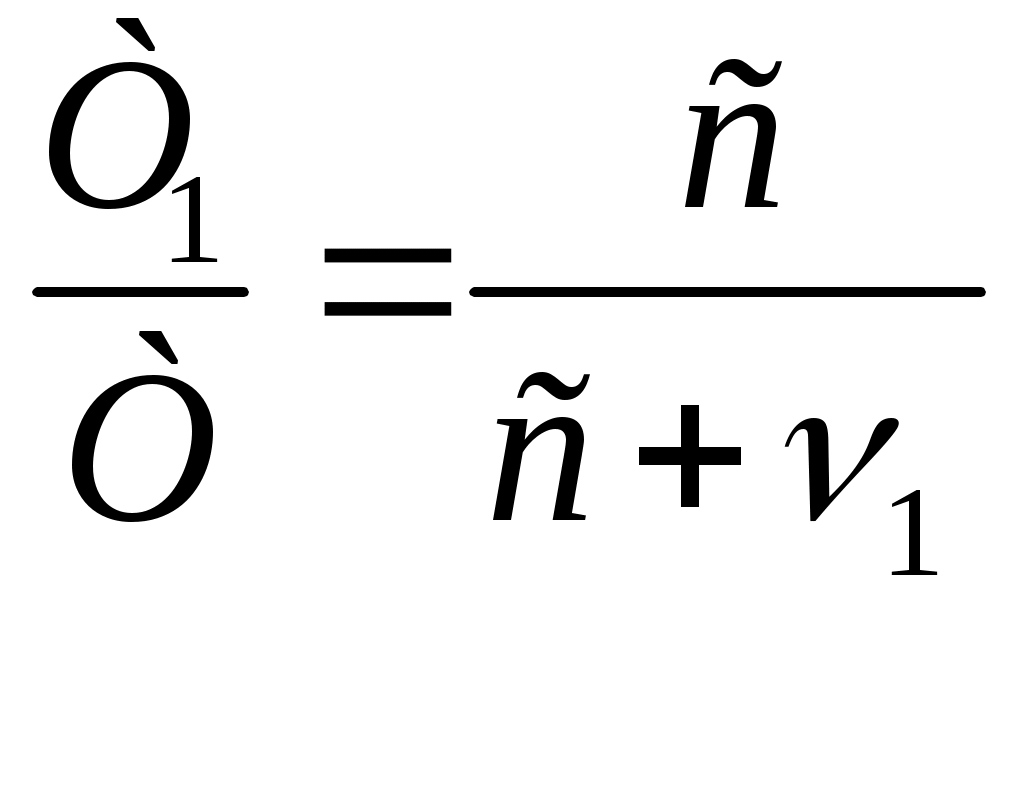 , (10.4) , (10.4)Если лодка останется неподвижной относительно водной поверхности, а источник колебаний i начнет перемещаться со скоростью v2 < c по направлению к приемнику A, как указано на рис. 9.11б, то воспринимаемая длина волны λ2 также уменьшится, но уже в иной пропорции. Так как поплавок движется в ту же самую сторону, что и волновой фронт, их относительная скорость будет равна разности двух скоростей: c – v2. Длина λ2 во столько раз меньше длины λ во сколько раз c – v2 меньше c; аналогично в отношении периода T2 и частоты f2: Важно подчеркнуть, что сокращение длины волны и периода колебаний при движущемся наблюдателе и покоящимся, источнике происходит за счет сложения скоростей c + v1, а при движущемся источнике и покоящемся наблюдателе это сокращение происходит уже по другому закону – за счет вычитания скоростей: c – v2. Таким образом, благодаря эффекту Доплера принцип относительности движения источника и приемника волн нарушается: по измеренным параметрам волнового процесса всегда можно определить, что относительно чего движется – либо источник движется относительно приемника, либо приемник движется относительно источника, другими словами, движение источника и приемника носит абсолютный характер. Если в рассмотренных двух случаях направления скоростей v1 и v2 изменить на противоположные, то в обоих случаях будет наблюдаться увеличение длины волны и периода колебаний, которое будет происходить тоже по различным законам. В табл. 10.2, помимо четырех типов раздельного движения источника и приемника колебаний, указаны еще четыре случая их совместного перемещения. Две последние формулы свидетельствуют: когда источник и приемник колебаний движутся в одном направлении с одинаковой скоростью, приемник будет регистрировать ту же самую длину волны, период и частоту колебаний, что и при покоящихся источнике и приемнике. Следовательно, такие приборы, как интерферометр Майкельсона, в котором источник света и приемник (в качестве приемника могут выступать зеркала и экраны детекторов, где получают интерференционные полосы) перемещаются совместно, не пригодны для регистрации своего движения относительно светоносной среды (если предположить, что таковая имеется); все волновые процессы, включая интерференционную картину, в таких приборах будут происходить так, как будто бы прибор неподвижен. Таблица 10.2
Формулы, вошедшие в табл. 10.2, были получены Доплером, но все они носят частныйхарактер, так как справедливы только для случая, когда приемник A и источник i находятся на оси x и их векторы скорости v1 и v2 направлены строго по горизонтали. Поэтому современный радар – системы не имеют возможности измерении скорости при движении источника и приемника в разных направлениях. Выше перечисленные формулы справедливы; сейчас ставится задача по получению общих формул для длины волны λ' и частоты колебаний f в общем виде. Данную задачу разобьем на две подзадачи, рассматривающие отдельно движение наблюдателя A при покоящемся источнике i (рис. 10.12а), и движение источника i при покоящемся наблюдателе A (рис. 10.12б). На рис. 10.12а вычерчен треугольник 0AA', в котором сторону λ выразим через две другие стороны λ' и β1λ', а также через прилегающие к λ косинусы углов π – θ1 и θ1 – φ1, получим: λ = λ'cos(θ1 – φ1) + β1λ'cos(π – θ1) или 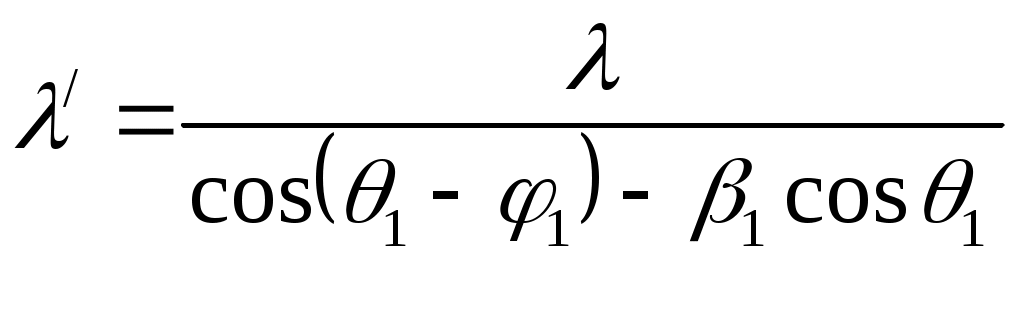 . (10.12) . (10.12)Из рис. 10.12б треугольник 0iA аналогичным образом находим формулу для измененной длины волны λ' для случая движения источника i при покоящемся наблюдателе A: λ' = λcos(θ2 – φ2) + β2λcos(π – θ2) или λ' = λ[cos(θ2 – φ2) – β2cos θ2]. (10.2) 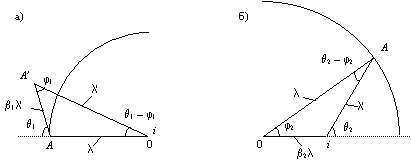 Рисунок 10.12. Геометрическая схема расположения источника i приемник A и волнового фронта, отвечающего длине волны λ. Имеем два случая: источник колебаний i покоится в точке 0, приемник A движется с относительной скоростью β1 по направлению к точке A' (а); приемник A покоится, источник i движется по горизонтали с относительной скоростью β2 (б). |