Пособие для подготовки к зачету _Основы сопротивления материалов. Учебнометодическое пособие для подготовки к зачету основы сопротивления материалов воронеж 2012 г. Ббк 30. 12

• Название: Учебнометодическое пособие для подготовки к зачету основы сопротивления материалов воронеж 2012 г. Ббк 30. 12
• Дата: 26.02.2023
• Размер: 435 Kb.
• Имя файла: Пособие для подготовки к зачету _Основы сопротивления материалов.doc
• Тип: Учебно-методическое пособие; #955470
• страница: 1 из 4

Федеральное агентство по образованию РФ ГОУ СПО

«Воронежский государственный

промышленно - технологический колледж».


Наумов О. Е.


ЭЛЕМЕНТЫ ТЕХНИЧЕСКОЙ МЕХАНИКИ

Учебно-методическое пособие для подготовки

к зачету

ОСНОВЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ


Воронеж 2012 г.
ББК 30.12

Данное методическое пособие представляет краткий сборник лекций по предмету «Элементы технической механики » студентов НПО профессии 30.20 «Автомеханик» и является дополнительным пособием для подготовки студентов к зачету и при выполнении расчетно-графических задач. Методическое пособие разработано в соответствии с рабочей программой по дисциплине, составленной на основе требований Государственного стандарта.

Рецензенты: профессор кафедры механизации

и проектирования машин ВГЛТА,

доктор технических наук

П.И. Попиков.

доцент кафедры «Транспортных машин» ВГАСУ,

преподаватель спецдисциплин ГОУ СПО «ВГПТК»,

кандидат технических наук

С.А.Никитин

Печатается по решению методического совета Воронежского государственного промышленно-технологического колледжа

Пояснительная записка.
Методическое пособие предназначено для студентов второго курса НПО специальности 30.20 «Автомеханик». Пособие составлено на основе образовательных стандартов и рабочей программы предмета «Элементы технической механики» при изучении курса объёмом 52 аудиторных часа. Оно является второй частью трех общих разделов курса ирассматривает вопросы

«Сопротивления материалов». В пособии в краткой форме изложены основные теоретические вопросы, определения, формулы, которые рассматриваются на занятиях со студентами. Материал построен таким образом, что по мере изучения основных формул и понятий каждой темы, студенту предлагается ответить на вопросы. Рассматриваемые вопросы относятся к зачетному материалу, на них студент будет отвечать по окончанию изучения всего курса. Полный список вопросов для подготовки к зачету и дополнительная литература, предложена в конце пособия.

В методическом пособии намеренно опущена часть поясняющих схем и графических рисунков, так как они подробно рассматриваются на уроках предмета «Элементы технической механики» и в процессе решения расчетно-графических задач.

Такой нестандартный подход позволяет дифференцированно обучать и оценивать знания студентов. Слабому студенту он дает возможность подготовить минимальный объем знаний для сдачи зачета, сильному - более углубленно и творчески изучить предмет, преподавателю - высвободить время для прямого диалога со студентами при изучении сложных тем и разделов предмета « Элементы технической механики ».

СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
1.1. Основные понятия

Сопротивление материалов это раздел технической механики изучающий способности материалов сопротивляться действию внешней нагрузки. В данном разделе рассматривают тела, которые под действием внешних сил меняют свою форму и размеры, т.е. деформиру­ются.

Что изучает сопротивление материалов?

Деформации могут быть упругими, если тело после устране­ния нагрузки, т.е. внешних сил, восстанавливает свои размеры и форму. Если же после снятия нагрузки тело не восстанавливает прежней формы, то возникающие при этом деформации назы­ваются остаточными. Здесь будем изучать только однородные изотропные тела, у которых по всем направлениям свойства оди­наковые.

Чем отличаются упругие деформации от остаточных?

В сопротивлении материалов тела классифицируют следую­щим образом:

• 
  пластина - у нее длина и ширина намного больше толщины;
  

• 
  оболочка - в отличие от пластины она ограничена криволи­нейными поверхностями;
  
• 
  брус - у него длина тела значительно больше его высоты и ширины. Если линия, соединяющая центры тяжести отдельных поперечных сечений бруса, прямая, то такой брус называют прямым;
  

• 
  стержень - брус, работающий на растяжение или сжатие;
  

• 
  балка - брус, к которому приложены силы под углом. В этом случае брус под действием таких сил будет работать не только на сжатие (растяжение), но и на изгиб, т.е. будет изгибаться.
  

В зависимости от того, какие силы приложены к брусу, он бу­дет по разному деформироваться. Чтобы определить напряжен­ное состояние, применяют метод сечений. Метод сечений позво­ляет выявить внутренние силы и заключается в том, что тело мыс­ленно рассекают плоскостью на две половины (рис. 1, а) и рас­сматривают равновесие какой либо отсеченной части. Считают, что внутренние 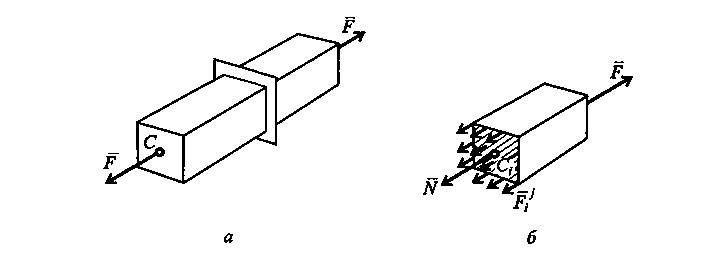силы распределены равномерно, их равнодейст­вующая равна N (рис. 1, б).


Рис. 1

Расскажите о методе сечения.

Составим уравнение равновесия сил, действующих на отсеченную часть бруса:

(1.1)
Отсюда N = F.

Величина а, характеризующая интенсивность распределения внутренних сил по поперечному сечению, называется напряжением:

(1.2)

где S - площадь поперечного сечения. Напряжение согласно Меж­дународной системе единиц измеряется в Па (Н/м²), а на практике чаще используют Н/см², Н/мм².

В рассмотренном примере внутренние силы направлены по нормали к поперечному сечению, поэтому напряжение называется нормальным.



Рис. 2.

В общем случае нагружения тела (рис. 2.) все внутренние силы можно привести к главному вектору Rи главному моменту М.

Выбираем систему координат так, чтобы ось zбыла направлена по нормали к сечению, а оси х и у расположим в его плоскости. Спроектировав главный вектор и главный момент на координат­ные оси, получим шесть уравнений для определения внутренних силовых факторов. Составляющая внутренних сил по нормали к сечению N - нормальная сила; силы Q_xи Q_yявляются составляю­щими поперечной силы Q. Момент относительно оси zназывают крутящим моментом (М_кр), а моменты М_хи М_у- изгибающими моментами относительно осей х и у. При заданных внешних силах все шесть внутренних силовых факторов могут быть определены из шести уравнений равновесия, составленных для отсеченной части бруса. Если в поперечном сечении возникает только нормальная внутренняя сила N, а прочие внутренние силовые факторы обра­щаются в нуль, то имеет место растяжение или сжатие, в зависимо­сти от направления силы N. Если в поперечном сечении возникает только момент М_кр, то брус в данном сечении работает только на кручение. В случае, когда внешние силы приложены к брусу таким образом, что в поперечных сечениях возникает только изгибающий момент М_х(или М_у), имеет место чистый изгиб в плоскости y_z(или x_z). Если в поперечном сечении наряду с изгибающим момен­том, например М_х, возникает и поперечная сила Q_yтакой случай нагружения называется поперечным изгибом (в плоскости у₂). Воз­можны и другие случаи, когда в поперечном сечении действуют раз­личные силовые факторы; при этом брус испытывает сложное на­пряженное состояние. Помимо нормального напряжения в сечении будет возникать касательное напряжение т в плоскости этого сечения.

Перечислите все внутренние силовые факторы возникающие в сечении бруса.

1.2. Растяжение и сжатие

Под растяжением понимается такой вид нагружения, при ко­тором в поперечных сечениях бруса (стержня) возникают только нормальные силы, а все прочие внутренние силовые факторы (по­перечные силы, крутящий и изгибающие моменты) равны нулю. Сжатие отличается от растяжения только знаком силы N: при растяжении нормальная сила N направлена от сечения (см. рис. 1), а при сжатии - к сечению. Поэтому при анализе внутренних сил сохраняется единство подхода к вопросам растяжения и сжатия. Исключение составят длинные тонкие стержни, для которых сжа­тие сопровождается изгибом.

Закон Гука. Многочисленные наблюдения за поведением твер­дых тел показывают, что в подавляющем большинстве случаев перемещения в определенных пределах пропорциональны дейст­вующим силам. Впервые в 1676 г. Гуком был сформулирован закон о том, что «какова сила, такова и деформация».

В современной трактовке закон Гука определяет линейную за­висимость между напряжением и деформацией:
(1.3)
Здесь коэффициент пропорциональности Е есть модуль упругости первого рода, ε - деформация, которую для однородного стержня можно определить как
(1.4)
Величину ε иногда называют относительным удлинением стержня длиной l, удлинение которого под действием приложенной силы составило Δl.

Модуль упругости первого рода является физической констан­той материала; он определяется экспериментально. Для наиболее часто встречающихся материалов его значения приведены в табл. 1 .

Запишите закон Гука при растяжении (сжатии)

Удлинение стержня. Если в закон Гука вместо напряжения под­ставить = N/S, а вместо деформации , то для стержня, у которого на длине l внутренняя нормальная сила постоянная и поперечное сечение не изменяется, получим выражение для опре­деления удлинения стержня:
(1.5)
При решении многих практических задач возникает необхо­димость наряду с удлинением, обусловленным напряжением а, учитывать также удлинения, связанные с температурным воз­действием.

В этом случае деформацию рассматривают как сумму силовой и чисто температурной деформации:
(1.6)
где - коэффициент температурного расширения материала. Для однородного стержня, нагруженного по концам и равномерно нагретого, имеем

(1.7)

Что такое относительное удлинение , и от чего он зависит?

Построение эпюр. График изменения нормальной силы, напря­жений и перемещений стержня вдоль его оси называется эпюрой соответственно нормальных сил, напряжений и перемещений. Эпюры дают наглядное представление о законах изменения раз­личных исследуемых величин. Построение эпюр рассмотрим на конкретном примере.