Пособие для подготовки к зачету _Основы сопротивления материалов. Учебнометодическое пособие для подготовки к зачету основы сопротивления материалов воронеж 2012 г. Ббк 30. 12
 Скачать 435 Kb.
|
Пример 1Для бруса, изображенного на рис.3,а, построить эпюры внутренних сил, напряжений и перемещений по длине бруса. Решение. 1.Выбираем начало отсчета в неподвижном сечении (точка О); положительное направление оси zнаправим по оси бруса, т.е. вниз. 2.Определим реакцию, составив одно уравнение равновесия: N0 - 3F + F = 0. Отсюда N0 =2F. 3.Построим эпюру внутренних сил N. Для этого на расстоянии z1рассечем брус и рассмотрим равновесие нижней части (рис. 3, б): 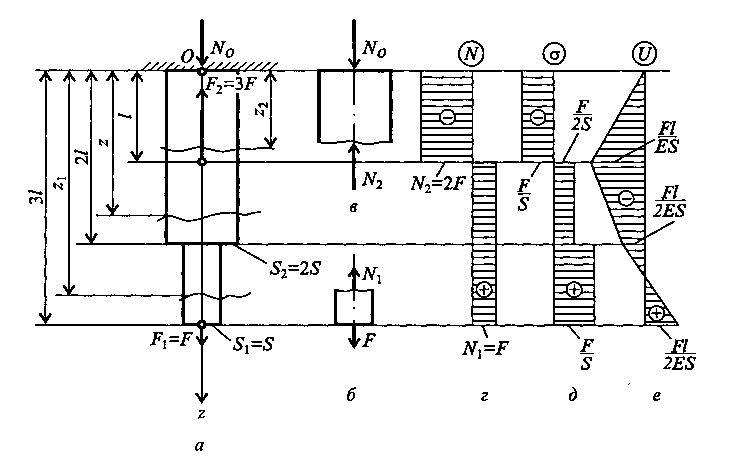 Рис. 3 ∑ Fiz = 0; - N1 + F = 0 Отсюда N1 =F, что справедливо для l ≤ z1 ≤ 3l. В этих пределах в брусе возникает растяжение, так как продольная сила N1направлена от сечения. Теперь выберем второй участок бруса 0 ≤ z2 ≤ l и рассмотрим равновесие верхней части (рис. 3, в): ∑ Fiz = 0; N0 - N2 = 0; 2F – N2 = 0 ОтсюдаN2 = 2F. Поскольку N2направлена к сечению, то брус под действием сил N0и N2сжимается. После того как определили все внутренние нормальные силы, переходим к построению эпюры нормальных сил (рис. 3, г). Вправо будем откладывать положительные значения, а влево - отрицательные значения нормальных сил. Анализируя построенную эпюру (N) , заметим, что внутренние силы не зависят от размеров поперечного сечения, а зависят только от приложенных внешних сил. Поэтому длину бруса разбивают на такое число участков, сколько сил на его длине приложено. В данном случае было два участка. При проверке правильности построения эпюры следует обратить внимание на то, что на эпюре внутренних сил в тех сечениях, где были приложены внешние силы, должны быть скачки, равные приложенной внешней силе. 4. Построим эпюру напряжений (σ). Брус следует разбить на участки. Поскольку σ = N/S, то участков на эпюре будет столько, сколько раз меняется поперечное сечение; при этом следует обращать внимание, чтобы при постоянной площади поперечного сечения нормальная сила на эпюре Nоставалась неизменной. С учетом этого на эпюре (σ) будут три различных значения σ (рис. 2.3, д): σ1 = N1/ S1 = F/S; σ2 = N2/S2 = F/2S; σ3 = N2/S2 = -2F/2S = -F/S. 5.Строим эпюру перемещений (U). Начинать следует от неподвижного сечения, т.е. от сечения О. Выразим перемещение сечения, находящегося от неподвижного на расстоянии z2:  Если 0 ≤ z2 ≤ l , то для z2 = l перемещении  Для l ≤ z ≤ 2l  Или  при z = 2l  Для 2l ≤ z1 ≤ 3l  при z1 = 3 l  где σ – продольное напряжение в сечении бруса; S – площадь поперечного сечения в характерной точке; l – длина характерного участка; Е – модуль упругости материала; U – перемещение деформируемого участка. Откладываем вычисленные перемещения на эпюре (U) (рис. 3, e). Какие необходимо построить эпюры чтобы выполнить расчет на прочность при растяжении? Диаграмма растяжения. Наиболее наглядно особенности диаграммы растяжения можно показать на примере испытания образца из малоуглеродистой стали (рис. 4). Диаграмма вычерчена в координатах F,Δl. На кривой можно выделить четыре зоны. Зона ОАносит название зоны упругости. Здесь материал подчиняется закону Гука и  . (1.8)где S – площадь поперечного сечения в характер- ной точке; l – длина характерного участка; Е – модуль упругости материала; F– внешняя сила;  - удлинение деформируемого участка.На рис. 4 этот участок для большей наглядности показан с отступлением от масштаба. Удлинения на участке ОА очень малы, и прямая ОА, будучи вычерченной в масштабе, совпадала бы в пределах ширины линии с осью ординат. Значение силы, для которой справедлив закон Гука, зависит от размеров образца и физических свойств материала, поэтому при дальнейшем рассмотрении диаграммы растяжения ее перестраивают в координатах σ и ε Зона АВназывается зоной общей текучести, а участок АВ - площадкой текучести. Здесь происходит существенное изменение длины образца без заметного увеличения нагрузки. Не все металлы имеют площадку текучести. Например, у алюминия, отожженной меди, легированных сталей площадка текучести не обнаруживается. Зона ВСназывается зоной упрочнения. Здесь удлинение образца сопровождается возрастанием 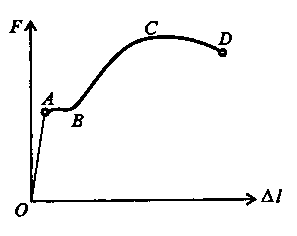 Рис.4 нагрузки. В стадии упрочнения на образце намечается место будущего разрыва и начинает образовываться так называемая шейка – местное сужение образца. При дальнейшем растяжении образца шейка быстро прогрессирует. Начиная с точки С удлинение образца происходит с уменьшением силы, но среднее напряжение в поперечном сечении шейки возрастает. Удлинение образца носит в этом случае местный характер, по этому участок CDназывается зоной местной текучести 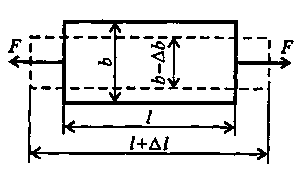 Рис.5 Точка Dсоответствует разрушению образца. Какая зона на диаграмме растяжения сжатия является зоной упрочнения и почему?  Относительная поперечная деформация. При растяжении (сжатии) прямого бруса кроме продольной деформации е происходит изменение поперечных размеров бруса (рис.5). Ширина бруса bпри растяжении уменьшается на Δb. Если Δb отнести к первоначальной ширине, то получим выражение для определения относительной поперечной деформации: (1.9)Отношение относительной поперечной деформации к относительной продольной деформации называют коэффициентом Пуассона и обозначают  : (1.10)Коэффициент Пуассона, так же как и модуль упругости Е, характеризует физические свойства материала; его значение колеблется для металлов в пределах от 0,25 до 0,35. Некоторые значения коэффициента приведены в табл. 1. 1.3. Основные механические характеристики материалов Механические свойства материалов устанавливают опытным путем, испытывая образцы на растяжение. Затем диаграмму растяжения перестраивают в координатах  и  . Как видно из рис. 6, она имеет такой же вид, как и в координатах F, Δl (см. рис. 4), но эта кривая будет характеризовать уже не свойства образца, а свойства материала. Отметим на этой диаграмме характерные точки.Наибольшее значение напряжения, до которого материал следует закону Гука, называется пределом пропорциональности σп. Упругие свойства материала сохраняются до значений напряжения, называемого пределом упругости. Под пределом упругости σу понимается такое наибольшее значение напряжения, до которого материал не получает остаточных деформаций. На практике предел пропорциональности и предел упругости трудно поддаются замеру, поэтому значения п и у в справочные данные по свойствам материалов обычно не включаются.Более определенной характеристикой является предел текучести. Под пределом текучести понимается такое значение напряжения, при котором рост деформации происходит без заметного увеличения нагрузки. В тех случаях, когда на диаграмме отсутствует явно выраженная площадка текучести, за предел текучести условно принимают такое значение напряжения, при котором остаточная деформация составляет 0,2%. В этом случае условный предел текучести будет обозначаться через σ0,2 .Если необходимо отличить предел текучести при растяжении от предела текучести при сжатии, то в обозначение вводится дополнительный индекс «р» или «с» (σтр и σтс). Предел текучести легко определяется экспериментально, поэтому он является одной из основных механических характеристик материала Что такое предел упругости и предел текучести , и от чего они зависят? Отношение максимальной силы, которую способен выдержать образец, к его начальной площади поперечного сечения называется пределом прочности, или временным сопротивлением разрыву - σвр (сжатию - σвс). Следует заметить, что σвр не является тем значением напряжения, при котором разрушается образец. Фактическое напряжение, при котором образец 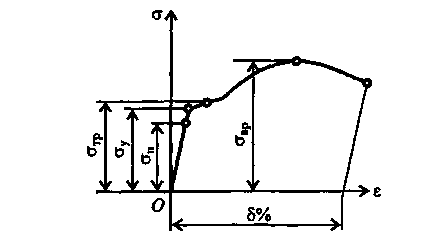 Рис. 6 Фактическое напряжение, при котором образец разрушается, будет больше, так как площадь поперечного сечения в этот момент меньше первоначальной площади вследствие образования шейки (на диаграмме напряжение подсчитывается относительно первоначальной площади поперечного сечения образца). Значение σвр является сравнительной характеристикой прочностных свойств материалов и часто используется при расчетах. При испытаниях на растяжение определяется еще одна характеристика материала - так называемое удлинение при разрыве δ %. Удлинение при разрыве представляет собой значение средней остаточной деформации, которая образуется к моменту разрыва на определенной стандартной длине образца. За стандартную длину образца принимают либо l0 = 10 d, либо l0 = 5d, где d- диаметр образца. До какого значения напряжения справедлив закон Гука? Значения механических характеристик некоторых наиболее часто встречающихся материалов приведены в табл. 1. Используя тбл.1 объясните, как от значения напряжения зависит удлинение образца. Таблица 1.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||