Пособие для подготовки к зачету _Основы сопротивления материалов. Учебнометодическое пособие для подготовки к зачету основы сопротивления материалов воронеж 2012 г. Ббк 30. 12

• Название: Учебнометодическое пособие для подготовки к зачету основы сопротивления материалов воронеж 2012 г. Ббк 30. 12
• Дата: 26.02.2023
• Размер: 435 Kb.
• Имя файла: Пособие для подготовки к зачету _Основы сопротивления материалов.doc
• Тип: Учебно-методическое пособие; #955470
• страница: 3 из 4

1.4. Расчеты на прочность при растяжении и сжатии
Размеры элементов конструкции следует подбирать так, чтобы обеспечить их прочность в работе при наименьшей затрате мате­риала. На основании анализа конструкции выявляется та точка, где возникают наибольшие напряжения σ_наиб. Найденное значение напряжения сопоставляется с допустимым значением напряжения для данного материала и конструкции.

Когда конструкция находится в стадии проектирования, то за­даются коэффициентом запаса п. Он назначается из конкретных условий работы рассчитываемой конструкции. В каждой области техники уже сложились свои традиции, свои требования и спе­цифика расчетов. Например, при проектировании строительных сооружений, рассчитанных на долгие сроки эксплуатации, запасы принимаются довольно большими (п_в= 2...5). Индекс «в» показы­вает на то, что запас вычисляется от предела прочности σ_в. В авиационной технике, где на конструкцию накладываются ог­раничения по массе, коэффициенты запаса также определяются по пределу прочности, но составляют п_в - 1,3... 2,0.

Значение коэффициентов запаса зависит и от свойств материала. В случае пластичного материала коэффициент запаса берется от предела текучести (п_Т= 1,5...2,0), а для хрупких материалов запас рассчитывается от предела прочности и принимается п_ъ= 2,5...4,0.

Назначив коэффициент запаса, для данного элемента конструк­ции рассчитывают допускаемое напряжение

или (1.11)

Выбрав допускаемое напряжение, составляют условие

σ_наиб ≤ [σ ] (1.12)
где - допускаемое продольное напряжение;

σ_т ; σ_в - напряжение текучести и выносливости

материала.

из которого определяют размеры проектируемого элемента.

Для чего вводится понятие допускаемого напряжения?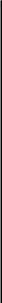
1.5. Срез и смятие
Напряжения и деформации при сдвиге (срезе). Ранее уже упоминалось, что в поперечном сечении могут возникать как нормальные σ, так и касательные напряжения τ. Если к короткому брусу, жестко заделанному одним концом в стену (рис.7, а),перпендикулярно к оси бруса приложить силу F, то в поперечных сечениях возникнет внутренняя поперечная сила Qв плоскости сечения, а следовательно, и касательное напряжение
τ = Q/S. (1.13)
где τ – касательное напряжение ;

Q – поперечная сила в сечении бруса;

S – площадь сечения участка .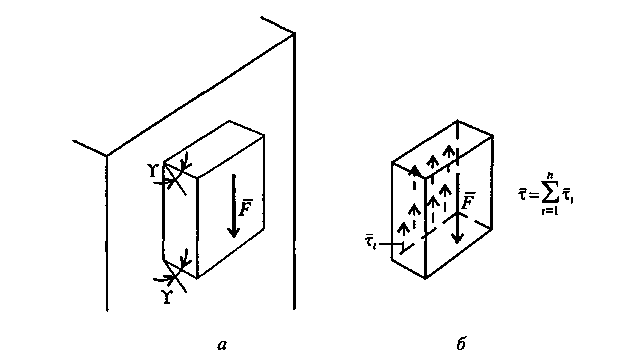



Рис. 7

Параллельные сечения бруса сдвигаются относительно друг друга (рис.7, б) так, что верхняя грань образует угол γ с горизон­талью. Установлено, что касательное напряжение τ прямо пропор­ционально угловой деформации γ:
τ = Gγ. (1.14)
Эта зависимость выражает закон Гука для сдвига. Явление среза можно наблюдать, если стальную полосу или бумагу перерезать ножницами, а также в случае, если к клепаному соединению при­ложена сила, большая, чем та, на которую данное соединение было рассчитано. На рис. 8 показано, что силы Fприложены в плоскости сечений; они вызывают деформацию сдвига, и может произойти срез заклепки. Вот почему сдвиг часто называют срезом.

Модуль упругости при сдвиге зависит от модуля упругости Iрода Е:
(1.15)
Если известны Е и μ , то модуль упругости при сдвиге можно определить. Например, для стали 30 Е = 2 ∙ 10⁵ Н/мм², μ = 0,3 , сле­довательно,


Подчеркнем, что сдвиг - это напряженное состояние. Если воз­никшие при сдвиге деформации находятся в пределах упругости, то после снятия нагрузки размеры и форма детали восстанавли­ваются. Если же деформации превысили предел упругости, то наблюдаются пластические деформации. После снятия нагрузки остается намеченное место среза. По достижении предельных на­пряжений произойдет срез.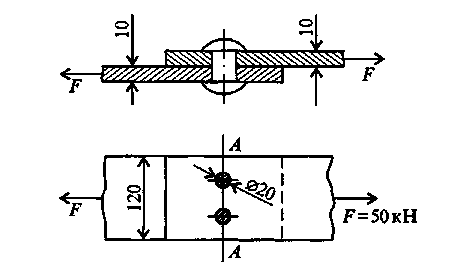



Рис. 8

Как вы понимаете деформацию сдвига и что такое модуль упругости при сдвиге?
Смятие. При сжатии двух тел возникает опасность смятия этих плоскостей. Напряжения, возникающие на контактирующих по­верхностях, называются напряжениями смятия. Смятие имеет место в заклепочных и болтовых соединениях. Напряжение смятия опре­деляют по формуле:
(1.16)
где F - сила, с которой сдавливаются контактирующие

поверх­ности,

S_см - площадь смятия.

Если поверхность смятия является криволинейной, то площадь смятия такой поверхности вычисляется как площадь проекции этой поверхности на плоскость, перпенди­кулярную к линии действия сминающей силы.

Объясните сущность деформации смятия.
1.6. Кручение
Под кручением понимается такой вид нагружения, при котором в поперечных сечениях возникает только крутящий момент. Про­чие внутренние силовые факторы (нормальная и поперечные силы, изгибающие моменты) равны нулю.

Рассмотрим кручение круглого бруса (рис. 9). К круглому брусу, жестко заделанному в стенку, на свободном торце прило­жен крутящий момент М.

В результате этого брус деформирует­ся: смежные сечения поворачиваются относительно друг друга, образующая ОВ искривляется и занимает положение ОС. При описании кручения принимаются следующие допущения и пра­вила:

• 
  ось бруса не деформируется;
  
• 
  поперечные сечения, плоские до деформации, после деформации также остаются плоскими;
  
• 
  продольные волокна не изменяют своей длины (угол у настолько мал, что изменением длины можно пренебречь);
  
• 
  радиусы rпоперечных сечений остаются прямыми после де­формации, поворачиваясь на некоторый угол φ;
  
• 
  для внутренних крутящих моментов принято следующее пра­вило знаков: если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит внутренний крутящий момент М_кр направленным против хода часовой стрелки, то момент счи­тается положительным.
  

Таким образом, при кручении в поперечном сечении бруса воз­никают касательные напряжения (чистый сдвиг).

Существуют понятия угла за­кручивания φ и относительного угла закручивания γ:
(1.17)
Касательные напряжения τ при кручении распределяются по се­чению неравномерно: в центре они равны нулю, а на макси­мальной окружности поперечно­го сечения - максимальному зна­чению τ_max.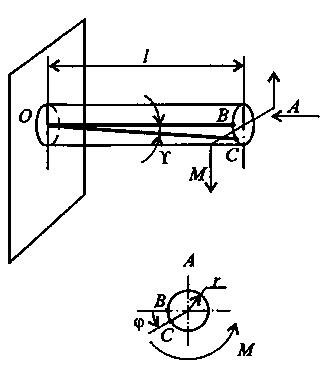



Рис 9
Поэтому расчет ве­дется по τ_max .Значение касательного напряжения зависит от внутреннего крутящего момента и геометрической характеристики поперечного сечения:
( 1.18)
где - есть полярный момент сопротивления сечения

Для сплошного поперечного сечения диаметром D:

W_p = 0,2 D³ (1.19)
Для кольцевого сечения (полый вал):
W_p = 0,2 D³( 1 – d⁴/D⁴)(1.20)
гдеd – внутренний диаметр отверстия ;

D– внешний диаметр вала.
Какие внутренние силовые факторы вызывают деформацию кручения , и какие напряжения возникают в сечении?
Построение эпюр. При кручении, как и при растяжении, строят эпюры внутренних силовых факторов ( M_кр крутящих моментов), напря­жений (τ_max) и перемещений (углов закручивания φ).

Построение эпюры М_кр. Всю длину бруса (рис. 10) разобьем на два участка. На эпюре внутренних силовых факторов в сечениях, где приложены внешние силы, будут скачки, равные приложен­ным нагрузкам (в данном случае - крутящим моментам). Приме­няя метод сечений с учетом правила знаков для крутящих момен­тов, строим эпюры М_кр. На рис. 2.10 для изображения внешних моментов применено условное обозначение в виде кружков: кру­жок с точкой обозначает силу, направленную на наблюдателя, а кружок с крестиком - силу, направленную от наблюдателя.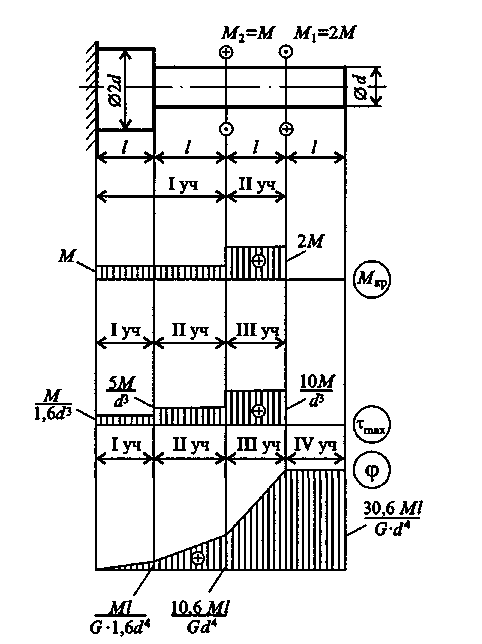


Рис. 10
Построение эпюры τ_max . Всю длину бруса разбиваем на три уча­стка; на каждом из них М_кр и W_pсохраняют постоянное значение. Затем подставляем в формулу (1.18)

τ_max =M_кр /W_p

соответствующие зна­чения М_кр и W_p:

на I участке

;

на II участке

;

на II участке

;

Поскольку все внутренние крутящие моменты имели положи­тельный знак, то и все касательные напряжения будут положи­тельны при построении их на эпюре τ_max

Построение эпюры φ. Прежде всего, необходимо установить за­висимость, по которой будем определять углы закручивания φ. На основании закона Гука для сдвига запишем выражение для мак­симального касательного напряжения в поперечном сечении круглого бруса, по аналогии с формулой для сдвига (1.14) :

τ_max = Gγ.

От чего зависит построение эпюры касательных напряжений при кручении?

Из рис. 9 видно, что при кручении образующая цилиндра ОВ поворачивается на угол у и занимает положение ОС. При этом дуга ВС равна γl; глядя на поперечное сечение по стрелке А, можно записать, что та же дуга ВС равна φr. Следовательно, γl = φr

откуда (1.21)
Подставляя найденное значение в закон Гука, получим

(1.22)
С другой стороны, , следовательно,

Выразим отсюда угол закручивания

(1.23)
Величину W_pr называют полярным моментом инер­ции сечения и обозначают J_p.

Полярный момент инерции для сплошного круглого бруса
J_p ≈ 0,1 D⁴(1.24)
для полого круглого бруса

(1.25)
Теперь угол закручивания запишем в виде
(1.26)
Произведение GJ_pназывают жесткостью бруса при кручении.

Что такое полярный момент инерции сечения и что он характеризует?
Итак, получена зависимость, по которой можно опреде-лять углы закручивания бруса.
Определять угол закручивания по этой зависимости можно только при условии, что на длине lвсе входя­щие в эту формулу величины - М_кр , J_p и G- постоянные.

Переходим к построению эпюры угловых перемещений. Вал по длине эпюры разбиваем на четыре участка. Так же, как и при по­строении эпюры перемещений при растяжении, начинаем строить эпюру от неподвижного сечения, т.е. от жесткой заделки. В конце первого участка угол закручивания будет



В конце II участка угол закручивания


В конце III участка


На IV участке угол закручивания будет равен углу закручивания φ_III, так как на этом участке отсутствуют внутренние крутящие мо­менты.

Вычисленные угловые перемещения откладываем на

эпюре φ.

Объясните, как построить эпюру углов закручивания деформируемого бруса.
1.7. Прямой поперечный изгиб

Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают изгибающие моменты. Если изгибающий момент является единственным силовым фактором, а поперечные и нормальные силы отсутствуют, то такой изгиб называется чистым. В большинстве случаев в поперечных сечениях бруса наряду с изгибающи­ми моментами возникают поперечные силы. В этом случае изгиб называют поперечным.

Брус, работающий в ос­новном на изгиб, называется балкой. На балку могут действовать сосре­доточенные силы и силы и моменты, а также распределенные по длине. Например, на рис. 11 F - сосредоточенная сила, М - сосредото­ченный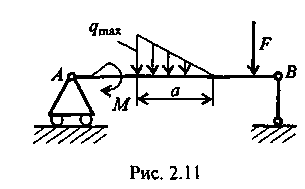



_{Рис .11}

момент; на участке а приложена распределенная нагрузка от нуля до q_max.

Что такое изгиб?
При описании явления изгиба используют геометрические ха­рактеристики поперечного сечения, учитывающие распределение материала по высоте сечения: J_x - момент инерции сечения отно­сительно главной оси, перпендикулярной к плоскости изгибаю­щего момента; W_x- момент сопротивления сечения при изгибе,
W_x= J_x/y_max, (1.27)
где y_max- координата точки, наиболее удаленной от нейтральной линии бруса (см.рис.12,б). Например, для прямоугольного сечения
(1.28)
где b- ширина;

h- высота сечения;

для круглого поперечного сечения
(1.29)
где D- диаметр сечения.

Что называется геометрической характеристикой сечения?
Анализ внутренних силовых факторов начинается с определе­ния полной системы внешних сил. Рассмотрим некоторые харак­терные примеры и установим правила определения изгибающих моментов и поперечных сил.

На рис. 12, а показана простейшая двухопорная балка, нагру­женная силой F. Освобождаем балку от связей и заменяем их дейст­вие реакциями. Опора А представляет собой невесомый стержень, поэтому реакция R_Aпойдет вдоль него. В шарнире В реакцию раскладываем на две составляющие. Несмотря на то, что выбор системы координат, безусловно, произволен, в сопротивлении материалов принято ось zнаправлять вдоль бруса; оси х и у должны лежать в плоскости, перпендикулярной к этой оси, причем поворот от оси х к оси у должен происходить против хода часовой стрелки,


Рис.12.
если смотреть с конца оси z(рис. 12, б). Начало отсчета для осей располагается в центре тяжести поперечного сечения. В этом случае оси х п у называются главными централь­ными осями поперечного сечения.

Составим уравнения равновесия для плоской системы сил и оп­ределим неизвестные реакции связей. Неизвестных величин три R_A, Y_B, Z_B. Уравнений статики тоже три, следовательно, задача статически определимая:
<sub>Σ Fiy = 0; +RA – F + YB = 0

Σ Fiy = 0; + ZB = 0

ΣmomB (Fi) = 0 ; - RJ + F(l – a) = 0</sub>

Отсюда находим реакции опор:
Z_B=0;

R_A=F(l-a)/l;

Y_B=Fa/l

Теперь приступим к выявлению внутренних силовых факторов в поперечных сечениях бруса. Для этого между точками приложе­ния внешних сил и моментов, воспользовавшись методом сече­ний, составляют уравнения равновесия отсеченных частей. Так, в конкретном примере необходимо делать сечения дважды: на рас­стоянии z, и z₂от левой опоры. На рис. 12, в показано, как рас­сечен брус на расстоянии z,. Следует обратить внимание на то, чтобы внутренние силовые факторы в поперечном сечении левой и правой частей были обязательно противоположны по направ­лению.

Из предыдущего материала уже известно, что внутренние си­ловые факторы определяются из уравнений равновесия отсечен­ных частей. Следует условиться о знаках поперечных сил и мо­ментов.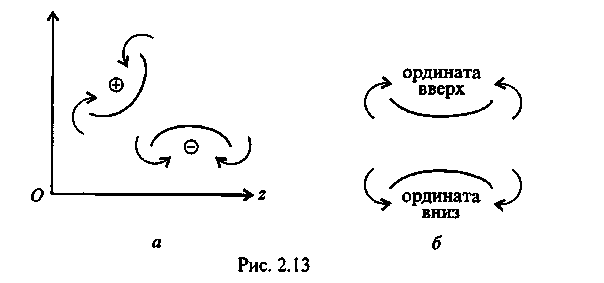



Рис.13.

Существует несколько способов определения знака изгибаю­щего момента в поперечном сечении.

1. По знаку кривизны изо­гнутого бруса (рис.13, а). Очевидно, знак будет зависеть от выбранной системы координат. Если ось у направить в противо­положную сторону, то знаки М_тгизменятся на противополож­ные.

2. Чаще всего при построении эпюр изгибающих моментов знак момента не зависит от выбранной системы отсчета, а орди­ната откладывается на сжатом волокне, т. е. в сторону вогнутости изогнутой оси бруса (рис. 13, б).

3. Если трудно представить, как будет выглядеть изогнутая ось бруса, то составляют сумму момен­тов сил, действующих на левую отсеченную часть бруса. Если равнодействующий момент всех сил, действующих на левую часть, будет направлен по часовой стрелке, то ордината изгибающего момента откладывается на эпюре вверх, т.е. момент. в поперечном сечении действует против часовой стрелки, а брус изгибается вогнутостью вверх, следовательно, ордината будет отложена на сжатом волокне. Если же сумма моментов, действующих слева от сечения, направлена против часовой стрелки, то изгибающий момент откладывается вниз (рис. 13, б).

Для сил, лежащих справа от сечения, имеет место обратная за­висимость.

Правило определения знака для поперечных сил: если равнодей­ствующая внешних сил, лежащих по левую сторону от сечения, на­правлена вверх, то поперечная сила в сечении считается положитель­ной, а если вниз, то поперечная сила отрицательна.

В сечении на расстоянии z_xот начала координат (т.е. в левой части бруса от сечения, см. рис. 12, в)поперечная сила Qимеет положительный знак и на эпюре будет откладываться вверх. При рассмотрении равновесия правой отсеченной части для сил, лежа­щих справа от сечения, имеет место обратная зависимость. Чтобы легче усвоить правила определения знаков, желательно рассмат­ривать равновесие, например, всегда левой части бруса. При построении эпюр изгибающих моментов и поперечных сил будет показан способ проверки правильности выбора знаков попереч­ных сил.
По каким принципам определяется знаки изгибающих моментов.

Построение эпюр изгибающих моментов и поперечных сил осуще­ствляется в следующей последовательности:

1) определяют реакции опор;

2) выявляют в поперечных сечениях бруса все внутренние силовые факторы (их значение и знак); 3) строят эпюры. Построим эпюры для балки, представленной на рис. 12, используя полу­ченные ранее вычисления.

1. Определяем реакции опор.

Составляем уравнения равновесия плоской системы сил:

R_A=F(l-a)/l; Y_B=Fa/l.

2. Определяем внутренние изгибающие моменты в поперечных сечениях балки. Для этого рассматриваем равновесие отсеченной левой части (рис. 12, в):

в сечении z₁



для 0 ≤ z₁ ≤ a

в сечении z₂



для a ≤ z₂ ≤ l

3.Определяем поперечные силы в сечении z<sub>1

Σ Fiy = 0; RA – Q = 0</sub>
Отсюда Q = R_A=F(l-a)/l;

в сечении z_{2 Σ Fiy = 0; RA – F + Q = 0}

Отсюда Q = Fa /l.

4. Строим эпюры изгибающих моментов.

Эпюра М_изг в пределах 0 ≤ z₁ ≤ а имеет линейную зависимость. Задаемся z₁= 0, при этом М_изг= 0. Откладываем эту точку на эпюре (рис. 14).

Далее при z₁= а; М_изг = F(l-a)a/l

В пределах a≤z₂ ≤ lполучаем:

при z₂ = a М_изг = F(l-a)a/l;

При z₂= l М_изг= 0.

Откладываем эти ординаты (они построены на сжатом волокне) и соединяем линиями. Следует заметить, что на втором участке можно было ординаты не вычислять, так как в шарнирной опоре В момент не может возникать, и поэтому на эпюре нужно сразу отложить 0.

5. Строим эпюры поперечных сил.

Как было выявлено в п. 3, поперечные силы постоянны на ка­ждом из двух участков, поэтому откладываем подсчитанные зна­чения с учетом знаков. Нужно обратить внимание, что в точке приложения внешней силы должен быть скачок, равный прило­женной силе.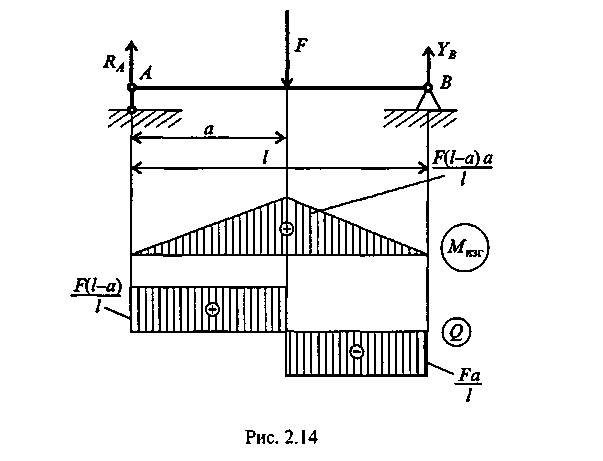



Рис.14
Кроме того, можно проверить правильность установленных знаков поперечных сил. Тангенс угла наклона линии М_изгна эпю­ре изгибающих моментов показывает на знак поперечной силы. Если угол острый, то тангенс положительный, а следовательно, и поперечная сила имеет знак плюс. Если угол наклона линии с осью zтупой, то поперечная сила отрицательная. Сопоставьте построенные эпюры М_изг и Q (см. рис. 14).
Объясните принципы построения эпюр поперечных сил и изгибающих моментов при изгибе бруса.



Напряжения в брусе при прямом чистом изгибе. Чистый изгиб в брусе может иметь место по всей длине бруса аb(рис. 15, а)или только на его части ab(рис. 15, б). При чистом изгибе в брусе возникают напряжения, непостоянные по высоте попереч­ного сечения. Из рис. 2.16 видно, что при изгибе бруса напряже­ние меняется от +σ_тaхдо -σ_maх. Следовательно, в поперечных сечениях есть недеформируемые точки, которые образуют ней­тральную линию, проходящую через центр тяжести поперечных сечений. Если изменение кривизны бруса происходит в плоскости, в которой действует изгибающий момент, и эта плоскость про­ходит через главные оси сечения, то такой изгиб называется прямым.

При прямом чистом изгибе
(1.30)

Расчет на прочность при изгибе по методике аналогичен расче­там на прочность при растяжении и кручении. Подсчитываются напряжения в сечениях по длине бруса и из них (по эпюре напря­жений) выбирается наибольшее. После чего из условия
( 1.31)
определяются геометрические размеры поперечного сечения бруса.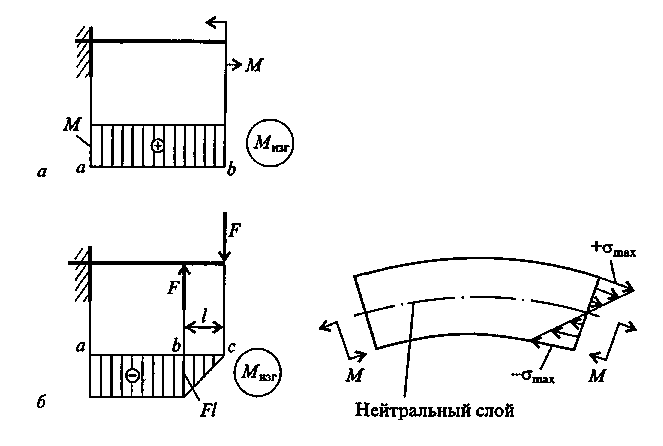



Рис. 15 Рис. 16

Пример 2

Определить диаметр круглого поперечного сечения бруса, нагруженного изгибающим моментом М = 600 кНм (см. рис. 15, а), если допускаемое напряжение [σ]_р = 160 Н/мм².

Решение.

1. 
   Поскольку эпюра изгибающих моментов уже известна, а брус имеет по­стоянное поперечное сечение, то определяем момент сопротивления
   

2.Определяем диаметр круглого бруса:


Какие напряжения возникают в поперечном сечении при изгибе ?

1.8. Устойчивость при осевом нагружении стержня
Под устойчивостью понимается свойство системы самостоя­тельно восстанавливать свое первоначальное состояние после того, как ей было сообщено некоторое отклонение от положения равно­весия. Если система таким свойством не обладает, то она называ­ется неустойчивой (говорят, что произошла потеря устойчивости).

Система, потерявшая устойчивость, может вести себя по разному, но переход к новому положению равновесия сопровож­дается большими перемещениями. Классическим примером неус­тойчивого равновесия является равновесие шарика на выпуклой поверхности (рис. 17, а). Малейшее отклонение от этого поло­жения приведет к тому, что шарик скатится вниз (рис.17, б, в). Попав в вогнутую поверхность, шарик будет находиться в состоя­нии устойчивого равновесия. Если теперь его вывести из этого состояния, отклонив влево или вправо, он вернется в первона­чальное положение.

Явление потери устойчивости можно наблюдать для упругих тел на целом ряде примеров. Наиболее простым случаем является потеря устойчивости центрально сжатого стержня (рис. 18). При достаточно большой силе стержень не сможет сохранить прямо­линейную форму и изогнется. Произойдет потеря устойчивости.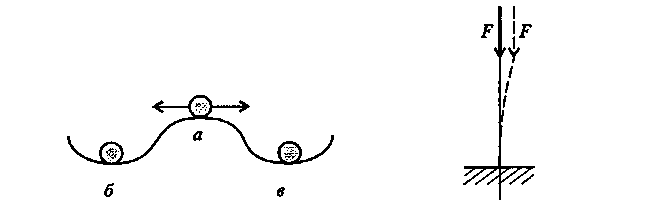



Рис..17 Рис. .18

Тонкостенная труба, нагруженная внешним давлением, также может потерять устойчивость. При этом круговая форма сечения переходит в эллиптическую, и труба сплющивается.

Что такое устойчивость?

Впервые задача об устойчивости стержня была поставлена и решена Л. Эйлером в середине XVIII в. Поэтому, когда речь идет об устойчивости сжатого стержня, употребляют выражение «устой­чивость стержня по Эйлеру». Эйлер определил значение первой критической (эйлеровой) силы для продольно сжатого стержня с шарнирным опиранием (рис. 19):
( 1.32)
По достижении критической силы F_крпрямолинейная форма равно­весия становится неустойчивой.

Продольно сжатые стержни не­обходимо проверять на устойчивость. Особенно опасен этот вид деформации при сжатии длин­ных стержней с небольшим осевым моментом инерции J.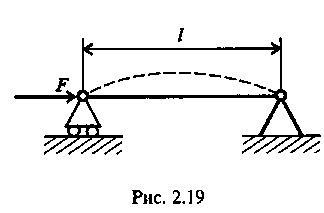



<sub>Рис.19

Как определяется эйлерова сила?</sub>