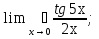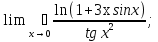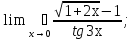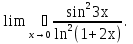Методичка Смирнова camb. Учебнометодическое пособие Ижевск Издательство Ижгту 2008 удк 51(075. 8)(076) з15
 Скачать 299.74 Kb. Скачать 299.74 Kb.
|
© Смирнова Н. А., составление, 2008 © Издательство ИжГТУ, 2008
1. Найти скалярное произведение векторов a и b, а ={1; 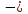 1;5}, b ={3;5;−8}. 1;5}, b ={3;5;−8}.2. Найти векторное произведение векторов а и b, а ={1; 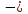 1;5}, b ={3;5; 1;5}, b ={3;5;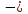 8}. 8}.3. Выбрать пару коллинеарных векторов: а) а ={1: 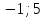 }, b ={ }, b ={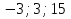 }; };б) а ={2; 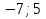 }, b ={2; }, b ={2;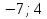 }; };в) а ={4;6; 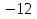 }, b ={ }, b ={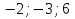 }; };г) а ={0;1;1}, b ={1;0;0}. 4. Выбрать пару перпендикулярных векторов: а) а = {1; 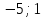 }, b = {3;5; }, b = {3;5;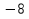 }; };б) а = {1; 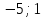 }, b ={4;9;1}; }, b ={4;9;1};в) а ={0;1;0}, b ={1;0; 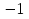 }; };г) а ={2;7}, b ={ 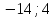 }. }.5. Выбрать тройки компланарных векторов: а) а = {1; 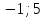 }, b = {3;5; }, b = {3;5;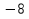 }, с = {1; }, с = {1;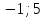 }; };б) а ={1; 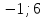 }, b ={ }, b ={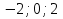 }, с ={1 }, с ={1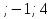 }; };в) а ={1;2;3}, b ={4;5;6}, с ={7;8;11}; г) а ={1;0;0}, b ={0;1;0}, с ={0;0;1}. 6. Пусть m = 2а + 3b. Тогда, если а = {1; 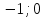 }; b = {2; }; b = {2;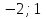 } , то } , то а)  = =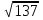 ; ;б)  =2; =2;в)  = =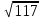 ; ;г) 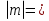 1,5. 1,5.7. Найти модуль вектора 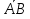 , если А(12; , если А(12;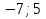 ), В(16;0; ), В(16;0;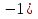 . .8. Найти направляющие косинусы для вектора а ={1;2 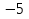 } . } .9. Найти площадь параллелограмма, построенного на векторах а и b: а ={1; 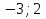 }, b ={2;0; }, b ={2;0;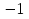 }. }.10. Вычислить площадь треугольника АВС, где А(1;2;0), В(3;2;1), С( 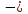 2;1;2). 2;1;2).11. Вычислить объем пирамиды АВСД, где А(5;1; 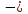 4), В(1;2; 4), В(1;2;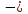 1), С(3;3; 1), С(3;3;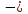 4), Д(2;2;2). 4), Д(2;2;2).12. Указать левую тройку векторов: а) а ={ 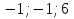 }, b ={ }, b ={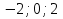 }, с ={1; }, с ={1;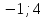 }; };б) а ={ 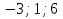 }, b ={ }, b ={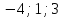 }, с ={ }, с ={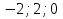 }; };в) а ={0;3;0}, b ={4;0;0}, с ={0;0;5}. 13. Выбрать утверждение, не соответствующее определению векторного произведения: а) векторным произведением векторов а и b является вектор с, перпендикулярный векторам а и b; б) 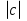 = = 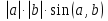 ; ;в) векторным произведением векторов а и b является вектор с, коллинеарный векторам а и b; г) векторы а, b, с образуют правую тройку. 14. Орт вектора по определению: а) проекция вектора на ось ОХ; б) направление вектора; в) единичный вектор, имеющий одинаковое направление с данным; г) любой вектор единичной длины. 15. Заданы векторы: а ={1;1;3}, b ={2;2;1}, с ={2;2; 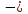 14}. 14}. Разложить вектор с по базису а, b. 16. Выбрать правильный ответ. Вектор а ={2;5} повернули на 90° против часовой стрелки, его новые координаты: а) { 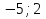 }; };б) { 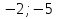 }; };в) {5; 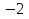 }; };г) { 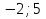 }. }.II. Элементы линейной алгебры 1. Выбрать правильный ответ. Обратная матрица существует: а) для любой матрицы; б) для любой квадратной матрицы; в) для квадратной матрицы, определитель которой не равен нулю; г) для квадратной матрицы, определитель которой неотрицателен. 2. Какое из нижеперечисленных свойств не является свойством определителя: а) если две строки (два столбца) поменять местами, то знак определителя изменится на противоположный; б) чтобы умножить определитель на число, нужно умножить на это число каждый элемент определителя; в) определитель равен сумме произведений элементов строки (столбца) и их алгебраических дополнений; г) если к какой-либо строке (столбцу) определителя прибавить линейную комбинацию других строк, то определитель не изменится? 3. Выбрать все правильные ответы. Элементарным преобразованием матрицы является: а) перемена местами двух строк или столбцов; б) умножение элементов строки (столбца) на число; в) транспонирование; г) прибавление к элементам строки (столбца) линейной комбинации параллельных строк (столбцов). 4. Какой из определителей равен 7? а) 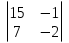 ; б) ; б)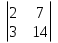 ; в) ; в)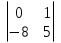 ; г) ; г)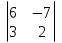 . .5. Выбрать правильное. (Aij – алгебраическое дополнение элемента aij определителя Δ). а) Δ = а21А11 + а22А12 + а23А13; б) Δ = а11А21 + а12А22 + а13А23; в) Δ = а11А11 + а21А12 + а31А13; г) Δ = а21А21 + а22А22 + а23А23. 6. Вычислить определитель: 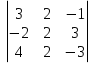 . .7. Установить правильное соответствие:
8. Установить правильное соответствие:
9. Исследовать систему на совместность 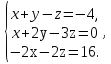 10. Укажите все пары матриц, которые можно перемножить между собой: A = 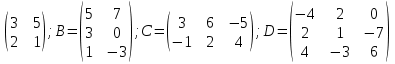 . . 11. Найти произведение матриц А и В: А = 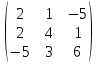 ; В = ; В =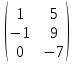 . .12. Найти обратную матрицу для А, если А = 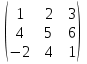 . .13. Найти ранг матрицы В = 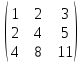 . .14. Решить матричное уравнение AXB=C, если A = 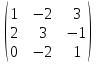 , B = , B =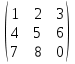 , C = , C =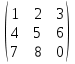 . .15. Решить систему линейных уравнений по формулам Крамера: 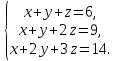 16. Выбрать правильный ответ. Собственные числа и собственные векторы матрицы А = 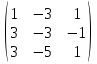 : :а) λ = 1, r =  ; б) λ = −2, r = ; б) λ = −2, r = 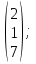 в) λ = 2, r = 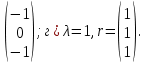
1. Установить правильное соответствие:
2. Установить взаимное расположение прямых: а) 3x + 5y – 9 = 0 и 10x − 6y + 4 = 0; б) 2x + 5y – 2 = 0 и x + y + 4 = 0; в) 2x + 3y = 8 и x+ y − 3 = 0; г) 2/3 x – 3/4 y −1 = 0 и 3/4 x + 2/3y + 2 = 0; д) x + 8 = 0 и 2x – 3 = 0. 3. Найти направляющий вектор прямой 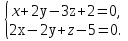 4. Указать вид уравнений прямой: а) 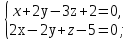 б) 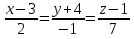 ; ;в) 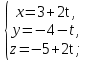 г) y = 3x +2; д) 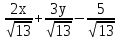 = 0; = 0;е) 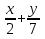 = 1. = 1.5. Найти площадь квадрата, если две его стороны лежат на прямых 5x – 12y – 65 = 0 и 5x – 12y + 26 = 0. 6. Найти нормальный вектор плоскости 4x + 2y – 11z + 18 = 0. 7. Плоскость задана тремя точками А (1; 0; −1), В (2; 2; 3), С (0; −3; 1). Записать ее уравнение. 8. Записать уравнение прямой, проходящей через точку М (0; −2; 0) перпендикулярно плоскости 2х − 3у + z + 6 = 0. 9. Найти расстояние от прямой 2x + y – 5 = 0 до начала координат. 10. На каком расстоянии от плоскости x + 2y – 2z − 9 = 0 находится точка М(3; 5; −2)? 11. Какая поверхность задана уравнением: а) 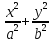 = z; = z;б) 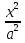 + + 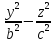 =1; =1;в) 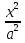 + + 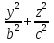 =1; =1;г) 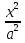 + + 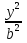 =1; =1;д) 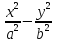 = z; = z;е) y2 = 2px; ж) 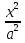 + + 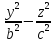 = = 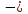 1. 1.12. Установить, какие линии определяются следующими уравнениями: а) x = 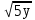 ; ;б) y = 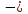 3 3 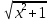 ; ;в) y = 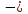 2 2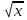 ; ;г) x = 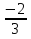  13. Составить уравнение параболы, вершина которой находится в начале координат. Парабола симметрична относительно оси ОХ и проходит через точку А (9; 6). 14. Найти полуоси, фокусы и эксцентриситет: а) гиперболы 16 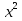 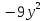 = = 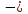 144; 144;б) эллипса 9 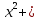 25 25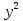 = 225. = 225.15. Определить, какие линии даны следующими уравнениями в полярных координатах: а) ρ = 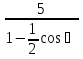 ; ;б) ρ = 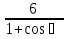 ; ;в) ρ = 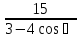 ; ;г) ρ = 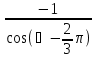 . .
1. Установить правильное соответствие:
2. Найти область определения функции: а) y = 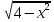 + 1; + 1;б) y = arccos 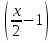 ; ;в) y = 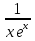 ; ;г)y= lg (3x−1) + 2lg (x+1). 3. Вычислить пределы:
4. Выбрать все верные утверждения. Для функции y = arctg 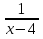 : :а) точка x = 4 является точкой разрыва I рода; б) точка x = 4 является точкой разрыва II рода; в) скачок функции в точке х = 4 равен π; г) в точке х = 4 функция непрерывна. 5. Найти точки разрыва функций: а) у = 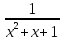 ; ;б) y = 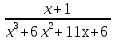 ; ;в) y = 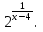 6. Выбрать правильный ответ. Функция y = 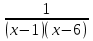 непрерывна на промежутке: непрерывна на промежутке:а) (2;5); б) (4;10); в) (0;7); г) (− 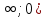 . .7. Установить правильное соответствие. Бесконечно малые эквивалентны (при α→ 0, β→∞):
8. Вычислить:
|

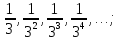
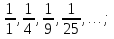
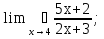
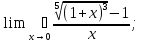
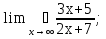
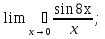
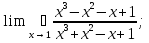
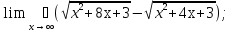
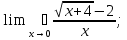
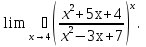
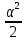 ;
;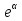 − 1;
− 1; 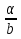 ;
;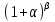 ;
;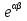 ;
;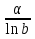 ;
;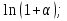
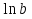 .
.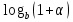 ;
;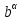 −1;
−1;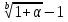 .
.