Методичка Смирнова camb. Учебнометодическое пособие Ижевск Издательство Ижгту 2008 удк 51(075. 8)(076) з15
 Скачать 299.74 Kb. Скачать 299.74 Kb.
|
|
Дифференциальное исчисление функций одной переменной
а) у = (1 + 4x2)3; б) у = sin2x; в) у = x arcsin(ln x) ; г) у = x2 e−2x; д) у = 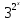 ; ;е) у = ln (x + 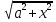 ; ;ж) у = xsinx; з) у = xlnx; и) y = 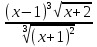 ; ;к) 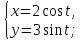 л) 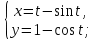 м) x3 + y3 = sin(x−2y); н) 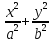 =1. =1.2. Установить правильное соответствие:
3. Выбрать правильный ответ. Уравнение касательной к параболе y2 = 4x в точке M(1;2) имеет вид: а) y = − x + 3; б) y = x + 1; в) y = 2x + 1; г) y = 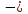 x +1. x +1.4. Выбрать правильный ответ. Уравнение нормали к кривой x2 + 2x y2 + 3y4 = 6 в точке В(1; −1) имеет вид: а) 4x + y – 3 = 0; б) x – 4y – 5 = 0; в) 4x – y – 3 = 0; г) –x – 4y – 5 = 0. 5. Найти дифференциал функции: а) y = arctg x; б) y = 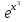 . .6. Вычислить приближенно, используя дифференциал: a) 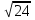 ; ;б) ln 1,02. 7. Найти дифференциал второго порядка для функций: а) y = 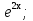 б) y = 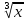 . .8. Найти точки, в которых касательная к гиперболе y = 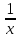 параллельна прямой y = − параллельна прямой y = − 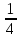 x + 3. x + 3.9. Вычислить с применением правила Лопиталя: a) 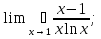 б) 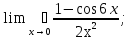 в) 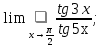 г) 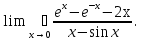 10. Найти производную n-го порядка функции y: а) y = sin x; б) 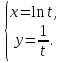
1.Установить правильное соответствие:
2. Найти обратную функцию для y = 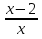 . .3. Какие из следующих функций являются монотонными: а) y = c; б) y = arctg x; в) y = sin2 x; г) y = 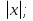 д) y = 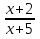 ; ;ж) y = – x2 + 2x. 4. Выбрать правильный ответ. Вертикальная асимптота графика функции у = 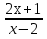 : :а) x = 2; б) y = 2; в) x = − 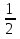 ; ;г) x = – 2. 5. Выбрать правильный ответ. Наклонная асимптота графика функции у = 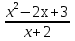 : :а) y = x + 2; б) x = – 2; в) y = x + 4; г) y = x – 4. 6. В каких из перечисленных точек функция у = 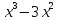 возрастает: возрастает:а) x = 3; б) x = 1; в) x = – 1; г) x = 0,5. 7. Найти точки перегиба функции y = (x + 1)2(x − 2). 8. Исследовать на экстремум функцию y = (x – 5)ex. 9. Найти наибольшее и наименьшее значения функции y = 3x – x2 на отрезке [−2;3]. 10. Функция f(x) = 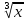 представлена в виде многочлена пятой степени относительно двучлена x – 1: представлена в виде многочлена пятой степени относительно двучлена x – 1: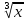 = 1+ = 1+ 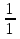 (x – 1) − (x – 1) − 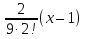 2 + 2 + 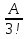 (x – 1)3 − (x – 1)3 − 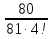 (x – 1)4 + (x – 1)4 +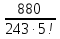 (x – 1)5+ R5, (x – 1)5+ R5,где R5 = 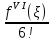 (x – 1)6, 1 < ξ < x. Найти А. (x – 1)6, 1 < ξ < x. Найти А.
1.Установить правильное соответствие:
2. На комплексной плоскости число z = −1 + i 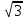 расположено: расположено:а) в I четверти; б) во II четверти; в) в III четверти; г) в IV четверти. 3. Для чисел z1 = − 1+2i и z2 = 2− i вычислить: а) сумму; б) произведение; в) частное. 4. Вычислить по формуле Муавра ( 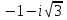 )15. )15.
1.Установить правильное соответствие:
2. Вычислить:
3. Почему, не вычисляя интеграла 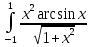 dx, можно сказать, что он равен нулю? dx, можно сказать, что он равен нулю?4. Выбрать все правильные ответы. Определенный интеграл применяется для нахождения: а) объeма тела вращения; б) площади плоской фигуры; в) ускорения тела; г) длины дуги кривой; д) площади поверхности вращения; е) работы переменной силы. 5. Найти площадь фигуры, ограниченной линиями у =sin x, у =cos x, x = 0. 6. Исследовать сходимость интегралов, сходящиеся вычислить: а) 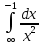 ; ;б) 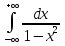 ; ;в) 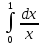 ; ;г) 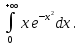 7. Вычислить среднее значение y = 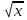 + +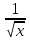 на отрезке [1;4]. на отрезке [1;4].8. Вычислить длину дуги кривой 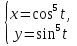 от t = 0 до t = от t = 0 до t = 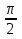 . . 9. Найти объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями y2 = x и x2 = y. 10. Оценить интеграл 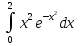 . .
1. Найти область определения функций: а) u = 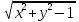 ; ;б) u = arcsin (x + y); в) u = y + 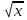 . .2. Найти частные производные для функций: а) u = x2 + 2y2 – 3xy 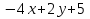 ; ;б) u = 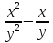 ; ;в) z = 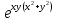 ; ;г) u = 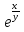 + + 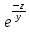 ; ;д) z = arctg 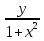 . .3. Найти полный дифференциал функции z = arctg 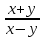 . .4. Найти 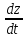 , если z = , если z = 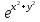 , x = a cos t, y = a sin t. , x = a cos t, y = a sin t.5. Составить уравнение касательной плоскости и нормали к поверхности z = x2 – 2xy+ y2− x + 2y в точке М (1; 1; 1). 6. Вычислить приближенно с помощью дифференциала 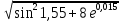 . .7. Выбрать правильный ответ. Градиент функции z = x2 + 3y2 в точке А(1;1) равен: а) {1;6}; б) 9; в) {1;8}; г) {−1;8}. 8. Найти экстремум функции z = x2+ xy+ y2 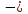 3x 3x 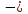 6y. 6y.9. Выбрать правильный ответ. Наибольшее и наименьшее значения функции z = xy + x + y в квадрате, ограниченном прямыми x = 1, x = 2, y = 2, y = 3: а) zнаим = 5; zнаиб = 11; б) zнаим = 3; zнаиб = 5; в) zнаим =5; zнаиб = 13; г) zнаим = −3; zнаиб = 4. Ответы
1. −42. 2. { 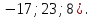 3. в). 4. б); в); г). 5. а); б). 6. а). 7. 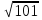 . .8. 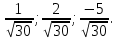 9. 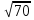 . .10. 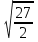 . .11. 4. 12. в). 13. в). 14. в). 15. с = − 6а + 4b. 16. а).
1. в). 2. б). 3. а), б), в), г). 4. б). 5. г). 6. 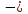 12. 12.7. а6; б3; в2; г5; д8; е1; з4. 8. а3; б2; в1. 9. Cистема совместна. 10. АС; ВС; СД; ДВ; СВ. 11. 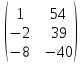 . .12. 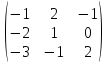 . .13. 2. 14.  . .15. 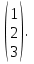 16. г).
1. а3; б4; в2; г1. 2. а) перпендикулярны; б) пересекаются; в) пересекаются; г) пер-пендикулярны; д) параллельны. 3. {− 4; 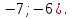 4. а) общее; б) канонические; в) параметрические; г) с угловым коэффициентом; д) нормальное; е) в отрезках. 5. 49. 6. {4; 2; −11}. 7. 16x – 6y – z = 0. 8. 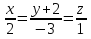 . .9. 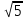 . .10. 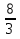 . .11. а) параболоид эллиптический; б) гиперболоид однополостный; в) эллипсоид; г) цилиндр эллиптический; д) параболоид гиперболи-ческий; е) цилиндр параболический; ж) гиперболоид двуполостный. 12. а) правая ветвь параболы; б) нижняя ветвь гиперболы; в) нижняя ветвь параболы; г) левая половина эллипса. 13. y2 = 4x. 14. а) 3; 4; F1(− 5; 0); F2(5; 0); ε = 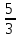 ; б) 5; 3; F1(− 4; 0); F2(4; 0); ε = ; б) 5; 3; F1(− 4; 0); F2(4; 0); ε = 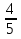 . .15. а) эллипс; б) парабола; в) гипербола; г) прямая.
1. а1; б3; в4; г2. 2. а) [ 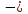 2;0) 2;0) 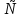 (0;2]; б) [0;4]; в) (−∞;0) (0;2]; б) [0;4]; в) (−∞;0) 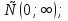 г) ( г) (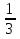 ; ;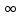 ). ).3. а) 2; б) 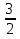 ; г) ; г) 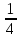 ; в) 0; д) ; в) 0; д) 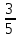 ; е) 8; ж) 2; з) e8. ; е) 8; ж) 2; з) e8.4. а); в). 5. а) функция непрерывна; б) х = –2; х = –3 − точки разрыва II рода; в) x = 4 – точка разрыва II рода. 6. а); г). 7. а1; б1; в1; г4; д2; е1; ж5; з1; и6; к1; л3. 8. а) 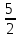 ; б) 3; в) ; б) 3; в) 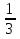 ; г) ; г)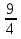 . .
1. а) 24x 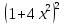 ; б) ; б) 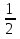 sin 2x; в) arcsin (ln x) + sin 2x; в) arcsin (ln x) + 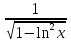 ; ;г) 2x e−2x(1 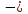 x); д) x); д) 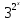 ln3 2x ln2 ; ln3 2x ln2 ;е) 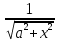 ; ж) xsin x ; ж) xsin x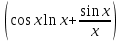 ; з) 2xlnx−1lnx; ; з) 2xlnx−1lnx;и) 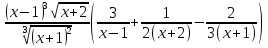 ; к) ; к) 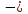 1,5 ctg t; л) 1,5 ctg t; л) 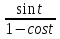 ; ;м) 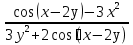 ; н) ; н) 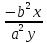 ; ;2. а7; б5; в9; г8; д10; е1; ж3; з6; и2; к4. 3. б). 4. а). 5. а) 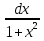 ; б) ; б) 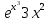 dx. dx.6. а) 4,9; б) 0,02. 7. а) 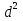 y = 4e2x dx2; б ) dy2 = − y = 4e2x dx2; б ) dy2 = −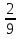 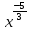 dx2. dx2.8. 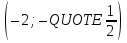 ; ; 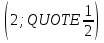 . .9. а) 1; б) 9; в) 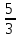 ; г) 2. ; г) 2.10. а) sin 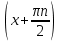 ; б) ; б) 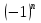 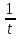 . .
1. а4; б1; в3; г2. 2. y = 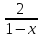 . .3. а); б); д). 4. а). 5. г). 6. а); в). 7. (0; 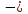 2). 2).8. в точке х = 4, ymin = − e4. 9. Наименьшее y = −18, наибольшее y = 2. 10. 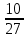 . .
1. а2; б3; в1. 2. б). 3. а) 3+ i; б) 4 + 3i; в) i. 4. 215.
1. а6; б5; в9; г7; д3; е1; ж10; з2; и12; к8; л4; м11; н13. 2.
3. Подынтегральная функция – нечетная. 4. а); б); г); д); е). 5. 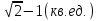 . .6. а) сходится, 1; б) сходится, 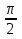 ; в) расходится ; г) сходится , ; в) расходится ; г) сходится , 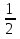 . .7. 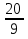 . .8. 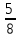 (2 (2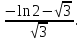 9. 0,3 (куб.ед.) 10. 0 ≤ 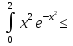 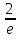 . .
1. а) x2 + y2 ≥ 1 – часть плоскости вне единичного круга: б) полоса между параллельными прямыми x + y ≤ 1 и x + y≥ − 1; в) полуплоскость x ≥ 0. 2. а) 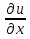 = 2x – 3y − 4; = 2x – 3y − 4; 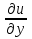 = 4y − 3x + 2. = 4y − 3x + 2.б) 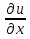 = = 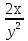 − − 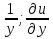 = = 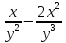 . .в) 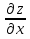 = = 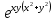 3x2y + y3; 3x2y + y3; 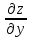 = = 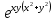 (x3+ 3xy2). (x3+ 3xy2).г) 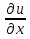 = = 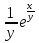 ; ; 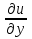 = − = − 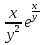 + + 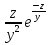 ; ; 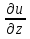 = − = − 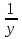 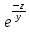 . .д) 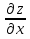 = = 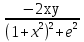 ; ; 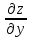 = = 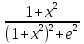 . .3. dz = 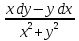 . .4. 0. 5. Касательная плоскость x − 2y + z = 0; нормаль 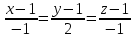 . .6. 3,02. 7. в). 8. zmin = − 9. 9. а). Список литературы
Задания по математике в тестовой форме для организации самостоятельной работы Учебно-методическое пособие Часть 1 Составитель Смирнова Наталья Анатольевна В редакции составителя Корректор Н. К. Швиндт |

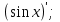
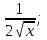
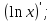
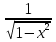 ;
;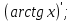
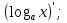
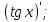
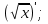
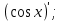
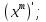
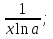
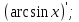
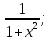
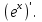
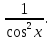
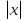 − 5
− 5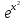 .
.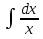 ;
;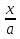 + C;
+ C;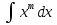 ;
;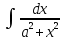 ;
;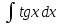 ;
;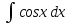 ;
;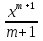 + С;
+ С;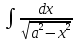 ;
;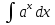 ;
;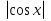 +C;
+C;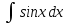 ;
;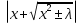 + C;
+ C;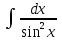 ;
;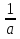 arctg
arctg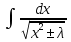 ;
;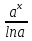 + C;
+ C;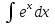 ;
;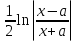 + C;
+ C;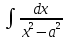 ;
;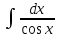 .
.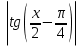 + C.
+ C.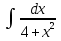 ;
;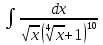 ;
;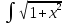 x dx;
x dx;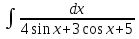 ;
;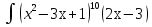 dx;
dx;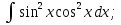
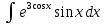 ;
;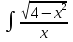 dx;
dx;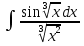 ;
;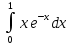 ;
;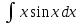 ;
;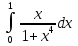 ;
;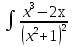 dx;
dx;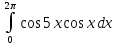 ;
;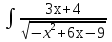 dx;
dx;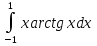 .
.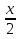 + C;
+ C;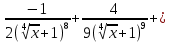 C;
C;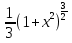 + C;
+ C;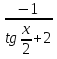 + C;
+ C;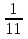
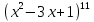 + C;
+ C;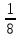 x -
x - 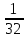 sin 4x + C;
sin 4x + C;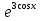 + C;
+ C;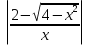 +
+ 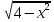 + C;
+ C;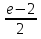 ;
; ;
;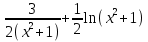 + C;
+ C;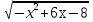 + 13 arcsin (x
+ 13 arcsin (x