ЛОГИКА уч.пособие МФЮА - Шнитман Г.В.. Учебнометодическое пособие москва 2006 Шнитман Г. В. Логика. Учебнометодическое пособие. М. Мфюа, 2006, 121 с
 Скачать 2.1 Mb.
|
19Исключающие и выделяющие сужденияИсключающие и выделяющие суждения следует характеризовать скорее всего не как категорические, то есть разновидность простых, а как некоторые сложные суждения. Общевыделяющие суждения. «Все S, и только S, суть Р», «Все S, но не только S, суть Р», «Ни одно S, и только S, не есть Р». Например, «Все S, и только S, суть Р» означает «Все S есть Р и ни одно не-S не есть Р», то есть два простых высказывания. Суждение «Все млекопитающие животные и только млекопитающие являются теплокровными» имеет смысл: «Все млекопитающие животные суть теплокровные животные и ни одно не млекопитающее животное не является теплокровным». Частновыделяющие суждения (вида 1, слово «только» относится к субъекту). 1) «Некоторые S, и только S, суть Р», 2) «Некоторые S, и только S, не суть Р». Данные высказывания эквивалентны:
Например, «Некоторые кислоты и только они образуют соли» эквивалентно «Некоторые кислоты образуют соли и ни одна не кислота не образует соли».
Например, «Некоторые лодыри и только они не сдадут этот экзамен» и «Все не-лодыри сдадут его». Частновыделяющие суждения (вида 2, слово «только» относится к кванторному слову). 1) «Только некоторые S есть Р». 2) «Только некоторые S не есть Р». Данные высказывания эквивалентны: «Некоторые S есть Р» и «Некоторые S не есть Р». Например, «Только некоторые студенты становятся профессорами» эквивалентно «Некоторые студенты становятся профессорами и некоторые студенты не становятся профессорами». Исключающие суждения. 1) «Все S, кроме R, суть Р» выражает сложное суждение: «Все S, которые не являются R, есть Р» и «Ни одно R не есть Р». Например, «Все спортсмены, кроме боксеров, вызывают у меня симпатию» эквивалентно «Все спортсмены не-боксеры вызывают у меня симпатию» и «Ни один боксер не вызывает у меня симпатию». 2) «Ни одно S, кроме R, не суть Р». 20Ограничения для сужденийВ традиционной силлогистике8 накладываются ограничительные условия на термины категорических атрибутивных высказываний: 1. при интерпретации терминов на некотором универсуме9 они обязательно должны оказаться знаками таких свойств, которые являются непустыми, т.е. для свойства, обозначенного термином Р, в универсуме должен найтись хотя бы один предмет а, который обладает этим свойством «а есть Р» (класс Р не является пустым). 2. при интерпретации терминов не некотором универсуме они обязательно должны оказаться знаками таких свойств, которые являются неуниверсальными, т.е. для свойства, обозначенного термином Р, и найдется по крайней мере один предмет b такой, что не обладает этим свойством «b не есть Р» (класс Р не является универсальным). Например, термины «русалка», «человек, достигший центра Земли», «Вечный двигатель» – пустые; если в качестве универсума берется класс людей, то нельзя использовать термин «разумное существо», так как класс разумных существ совпадает с классом людей (является универсальным). Поэтому, чтобы последними терминами мы могли пользоваться и могли рассматривать предложение вида «Каждый человек является разумным существом», необходимо взять более широкий универсум, чем класс людей. 21Семантика традиционной силлогистикиДля начала необходимо выделить и определить некоторый универсум рассуждения U. Истинность категорических атрибутивных высказываний можно определить в традиционной силлогистике через выполнимость для субъектов и предикатов отношений, задаваемых некоторыми модельными схемами. 1. Предложение «Всякий S есть Р» истинно тогда и только тогда, когда классы S и Р находятся в одном из следующих отношений: № 1 № 2  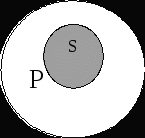 Например, «Всякий квадрат – это равносторонний прямоугольник» находится в отношении, задаваемом первой модельной схемой, и, следовательно, является истинным. «Всякий студент является учащимся» также является истинным, так как субъект и предикат этого высказывания находятся в отношении, задаваемом второй модельной схемой. 2. Предложение «Ни один S не есть Р» истинно тогда и только тогда, когда классы S и Р находятся в одном из следующих отношений: № 1 № 2 S Р 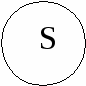  Примером истинного предложения, в котором субъект и предикат находятся в отношении, задаваемом первой модельной схемой, может служить предложение «Всякий юридически наказуемый поступок не есть преступление». Вторая модельная схема имеет место для субъекта и предиката предложения «Ни одно натуральное число не является иррациональным», и поэтому оно истинно. 3. Предложение «Некоторый S есть Р» истинно тогда и только тогда, когда S и Р находятся в одном из следующих отношений: № 1 № 2 № 3 № 4  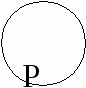 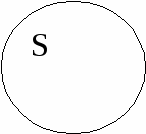 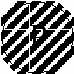  № 5 S Р  Примерами высказываний, субъекты и предикаты которых соответственно удовлетворяют каждой из данных модельных схем, будут: 1) «Некоторый квадрат есть равносторонний прямоугольник», 2) «Некоторые студенты являются учащимися», 3) «Некоторый учащийся – спортсмен», 4) «Некоторый писатель является поэтом», 5) «Некоторое натуральное число, меньше 100, является натуральным числом, большим 80». 4. Предложение «Некоторый S не есть Р» истинно тогда и только тогда, когда классы S и Р находятся в одном из следующих отношений: № 1 № 2 S Р    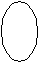№ 3 № 4 S Р 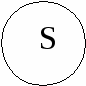№ 5 № 5   П 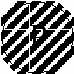римерами соответствующих высказываний для каждой модельной схемы будут высказывания: 1) «Некоторое натуральное число, меньшее 100, не является натуральным числом, большим 80», 2) «Некоторый учащийся не является спортсменом», 3) «Некоторый юридически ненаказуемый поступок не есть преступление», 4) «Некоторое натуральное число не является иррациональным», 5) «Некоторый писатель не является поэтом».5. Предложение «а есть Р» истинно тогда и только тогда, когда между предметом, обозначенным термином «а», и классом Р существует отношение, соответствующее схеме №1: Это значит, что предмет а является элементом класса Р. Например: «Д.И.Менделеев – химик», «2 – четное число», «Лондон – город» и т.д. 6. Предложение «а не есть Р» истинно тогда и только тогда, когда между предметом, обозначенным термином «а», и классом Р существует отношение, соответствующее схеме №2: № 1 № 2  а Это значит, что предмет а не является элементом класса Р. Например: «5 не является четным числом», «Наполеон не является англичанином» и др. |