ЛОГИКА уч.пособие МФЮА - Шнитман Г.В.. Учебнометодическое пособие москва 2006 Шнитман Г. В. Логика. Учебнометодическое пособие. М. Мфюа, 2006, 121 с
 Скачать 2.1 Mb. Скачать 2.1 Mb.
|
33Простой категорический силлогизм(Умозаключение из двух посылок) Рассмотрим двухпосылочные умозаключения вида: A1, А2 ╞ В. Простой категорический силлогизм – это умозаключение, в котором от наличия некоторых отношений между терминами S и М и терминами Р и М, фиксируемых в посылках, приходят к заключению о наличии определенного отношения между терминами S и Р. Общий термин, содержащийся в A1и А2, связывает посылки и опосредует следование из них заключения В. Поэтому умозаключения такого вида часто называются опосредованными. Примером силлогизма является умозаключение: Слово «бег» обозначает действие. Слово «бег» –- существительное. Некоторые существительные обозначают действия. В нем содержатся три высказывания: первые два являются посылками, а последнее – заключением. Средним термином является словосочетание «слово “бег”», связывающее термины посылок – «существительное» и «обозначает действие».
Будем далее называть посылку, содержащую меньший термин, меньшей посылкой, а посылку, содержащую больший термин, большей посылкой. Условимся также всегда помещать большую посылку на первое место, а под ней записывать меньшую посылку. Приняв эти условия, можно все простые категорические силлогизмы разделить по так называемым фигурам. Каждая фигура – это множество простых категорических силлогизмов, имеющих одну и ту же структуру, определяемую расположением среднего термина в посылках: 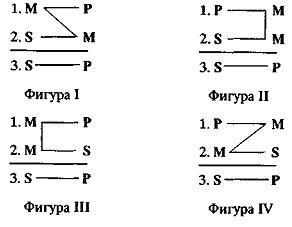 Здесь цифрой 1 обозначается большая посылка, цифрой 2 – меньшая посылка, а цифрой 3 – заключение. Буква S обозначает меньший термин, буква Р – больший, а буква М – средний термин. Очевидно, что средний термин можно расположить только указанными четырьмя способами, поэтому существуют только четыре различные фигуры. Если в фигуре указать тип высказываний, стоящих на местах посылок и заключения, то получим разновидность данной фигуры. Так, если взять I фигуру и предположить, что большая посылка, меньшая посылка и заключение – это высказывания типа а, то получим силлогизм (разновидность) I фигуры: 1. Всякий М есть Р 2. Всякий S есть М 3. Всякий S есть Р Такого рода разновидности фигур называются их модусами. В каждой фигуре имеется 64 модуса (разновидностей фигур), а по всем четырем фигурам – 256. Однако не во всех из них заключение логически следует из посылок. Те модусы, для которых следование имеет место, называются правильными. Всего существует (24) правильных модуса. Все они в средневековье получили специальные названия. Так, приведенный выше модус I фигуры называется Barbara(иногда пишут ааа, указывая последовательно слева направо тип высказывания большей, меньшей посылок и заключения).  Для Проверки правильности конкретных рассуждений, строящихся в форме простого категорического силлогизма, вовсе нет необходимости запоминать правильные модусы, знать их названия. Для этого можно воспользоваться семантическими условиями истинности категорических высказываний, задаваемых пунктами (1)-(4). Проверим, например, правильность рассуждения: 1. Ни одно ластоногое животное не есть рыба. 2. Все тюлени – ластоногие животные. 3. Ни один тюлень не является рыбой. Это рассуждение осуществляется по модусу CelarentI фигуры, имеющему вид: 1. Ни один М не есть Р 2. Всякий S есть М 3. Ни один S не есть Р Чтобы проверить его правильность, достаточно рассмотреть лишь такие модельные схемы, на которых посылки одновременно принимают значение «истина». Множество таких схем по трем переменным S, Р и М состоит в точности из следующих четырех модельных схем: 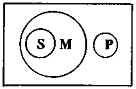 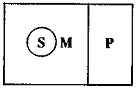 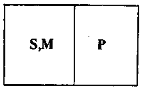 На каждой из этих схем термины М и Р, а также S и М находятся в таких отношениях друг к другу, что посылки «Ни один М не есть Р» и «Всякий S есть М» оказываются одновременно истинными. Проверяя теперь, в каком отношении на этих схемах находятся термины S и Р, обнаруживаем, что в каждой из них будет справедливо утверждать «Ни один S не есть Р», что и обосновывает наличие указанного следования. Обоснование модуса Celarentозначает, что умозаключение данной формы правильно для любых непустых и не универсальных терминов S, Р и М. Так, взяв в качестве S термин «правильный модус по I фигуре», в качестве Р – «физический закон» и в качестве М – «силлогизм», можем утверждать, что так как предложения «Ни один силлогизм не является физическим законом» и «Любой правильный модус по I фигуре – это силлогизм» истинны, то по модусу Celarentобязательно должно быть истинным и предложение «Любой правильный модус по I фигуре не есть физический закон». Модельные схемы позволяют не только устанавливать, но и опровергать наличие логического следования. Для этого необходимо сначала выявить логическую форму рассуждения, а затем указать хотя бы одну модельную схему, на которой посылки будут истинными, а заключение – ложным. Пусть проверяется рассуждение: 1. Некоторые вещества, ускоряющие химические реакции, не участвуют в реакции. 2. Все катализаторы являются веществами, ускоряющими химические реакции. 3. Все катализаторы не участвуют в реакции. Положив, что S – это «катализаторы», М – «вещества, ускоряющие химические реакции» и Р – «вещества, участвующие в химических реакциях», находим, что рассуждение имеет форму модуса оаеI фигуры, то есть 1. Некоторый М не есть Р (о) 2. Всякий S есть М (а) 3. Ни один S не есть Р (е) 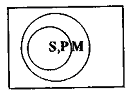 Приведенная сразу же под рассматриваемым силлогизмом модельная схема, как говорят в логике опровергает данный модус, так как на этой схеме обе посылки силлогизма будут истинными, а заключение – ложным. На основе этой схемы можно построить интуитивно более наглядный контрпример данному рассуждению. Для этого необходимо так подобрать термины S, P и М, чтобы посылки оказались истинными, а заключение – заведомо ложным. В нашем случае в качестве таких терминов можно взять, например, «треугольник» (М), «равносторонний треугольник» (Р) и «равноугольный треугольник» (S). Осуществляя теперь подстановку этих терминов в рассматриваемый модус оаеI фигуры, получим умозаключение с истинными посылками: 1. Некоторый треугольник не является равносторонним. 2. Всякий равноугольный треугольник – треугольник. и ложным заключением: 3. Всякий равноугольный треугольник не есть равносторонний треугольник. Данное рассуждение показывает, что умозаключение вида 1. Некоторый М не есть Р (о) 2. Всякий S есть М (а) 3. Ни один S не есть Р (е) не удовлетворяет отношению логического следования, так как имеются истинные посылки данного типа, при которых заключение оказывается ложным. Семантический метод решения вопроса о правильности модусов сталкивается с той трудностью, что число возможных модельных схем отношений между терминами быстро растет с увеличением числа терминов. Если для случая одного термина существует ровно одна модельная схема, для двух различных терминов существует ровно семь различных модельных схем, то уже в случае трех различных терминов число всех отличных друг от друга модельных схем увеличивается почти до 200. Это делает необходимым нахождение более простых и не столь громоздких способов проверки правильности модусов простого категорического силлогизма. Такой способ имеется. Он носит синтаксический характер и содержит перечень правил. Выполнение каждого правила является необходимым, а всех вместе – достаточным условием, чтобы считать некоторый модус правильным. Эти правила называются общими правилами силлогизма и подразделяются на правила терминов и посылок. Модус простого категорического силлогизма является правильным, если и только если он удовлетворяет правилам терминов и посылок. Правила терминов:
Правила посылок:
Эти правила позволяют при их использовании быстро и эффективно решать вопрос о правильности или неправильности модусов. Так, приводившийся пример модуса оаеI фигуры нарушает условие (1) и (2) для терминов, поэтому не является правильным модусом. Иногда для отдельных фигур указывают специальные их свойства, которые выполняются для всех правильных модусов этих фигур. Однако они не являются критериями правильности. Эти свойства таковы: по I фигуре:
по II фигуре:
по III фигуре:
В любом правильном модусе по I фигуре большая посылка – общее высказывание, а меньшая – утвердительная; в любом правильном модусе по II фигуре большая посылка – общее высказывание, одна из посылок отрицательна; в любом правильном модусе по III фигуре меньшая посылка – утвердительное высказывание, а заключение – частное. Еще раз подчеркнем, что эти свойства не являются критериям правильности, так как существует большое количество неправильных модусов, которые обладают указанными свойствами. |
