|
|
чЯч. Учебнометодическое пособие по курсу Методы вычислений для студентов ivv курсов всех форм обучения
Воронежский государственный университет
Математический факультет
Кафедра математического моделирования
Численное интегрирование и дифференцирование Учебно-методическое пособие
по курсу «Методы вычислений»
для студентов IV-V курсов
всех форм обучения
Составитель В.П.Трофимов
Воронеж
2002 г.
Настоящее учебно-методическое пособие предназначено для выполнения лабораторных работ «Численное интегрирование» и «Численное дифференцирование» по курсу «Методы вычислений» студентами IV-V курсов дневного и вечернего отделений математического факультета. Разработка может быть использована для самостоятельной работы студентов и при подготовке к экзамену.
Разработка представляет собой существенно переработанный и дополненный вариант методических указаний [6].
Литература
1. Бахвалов Н.С. Численные методы в задачах и упражнениях: Учеб. пособие / Н.С.Бахвалов, А.В.Лапин, Е.В.Чижонков; Под ред. В.А.Садовничего. – М.: Высшая школа, 2000. – 190 с.
2. Плис А.И. Лабораторный практикум по высшей математике: Учеб. пособие для втузов / А.И.Плис, Н.А.Сливина. – 2-е изд., перераб. и доп. – М.: Высшая школа, 1994. – 416 с.
3. Крылов В.И. Справочная книга по численному интегрированию/ В.И.Крылов, Л.Т.Шульгина. – М.: Наука, 1966. – 372 с.
4. Люстерник Л.А. Краткий курс функционального анализа / Л.А.Люстерник, В.И.Соболев. – М.: Высшая школа, 1982. – 328 с.
5. Вайникко Г.М. Анализ дискретизационных методов / Г.М.Вайникко. – Тарту.: Тартусский гос. ун-т, 1976. – 162 с.
6. Методические указания по методам вычислений и вычислительной практике. Часть II / Сост. Г.С.Аброськина, В.П.Трофимов. - Воронеж.: Воронеж. гос. ун-т, 1988. – 19 с.
Обозначения
R - множество вещественных чисел;
N – множество натуральных чисел;
С – множество комплексных чисел;
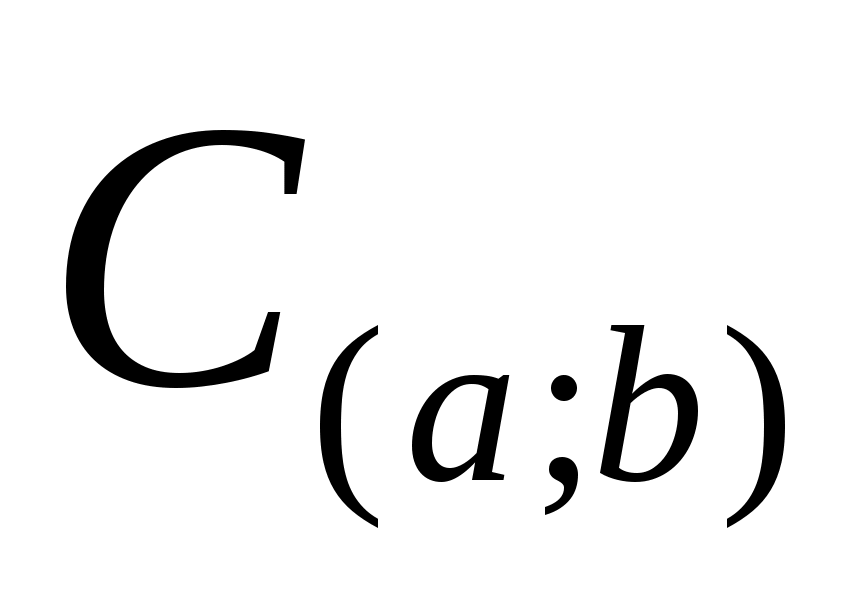 - банахово пространство функций непрерывных на - банахово пространство функций непрерывных на  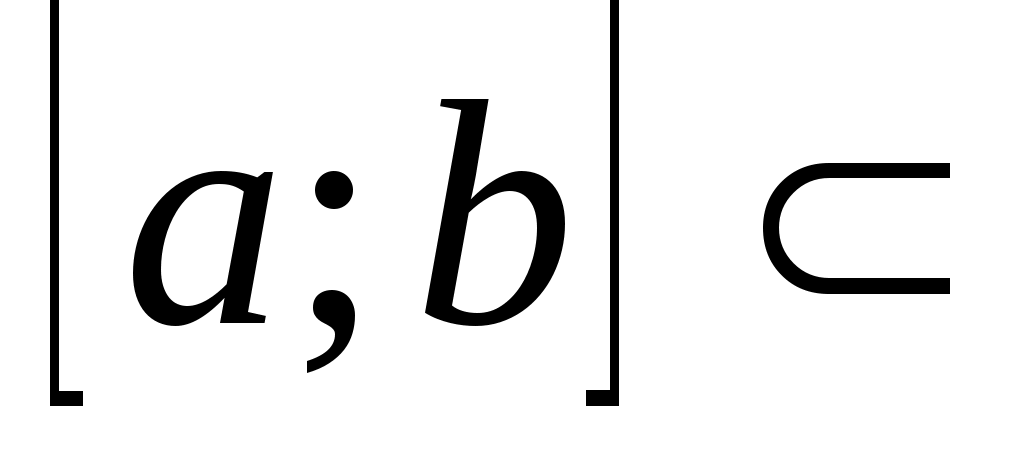 R; R;
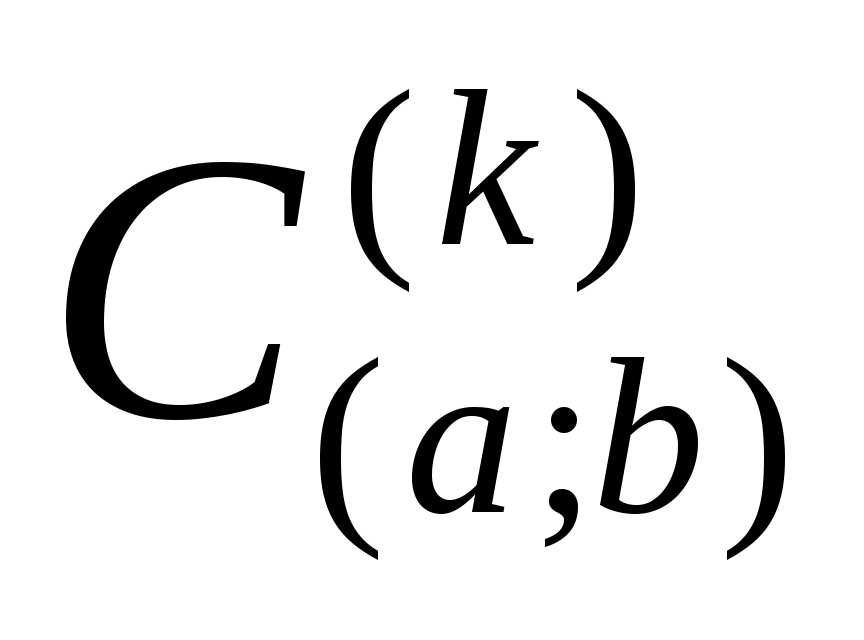 - пространство функций, имеющих на - пространство функций, имеющих на 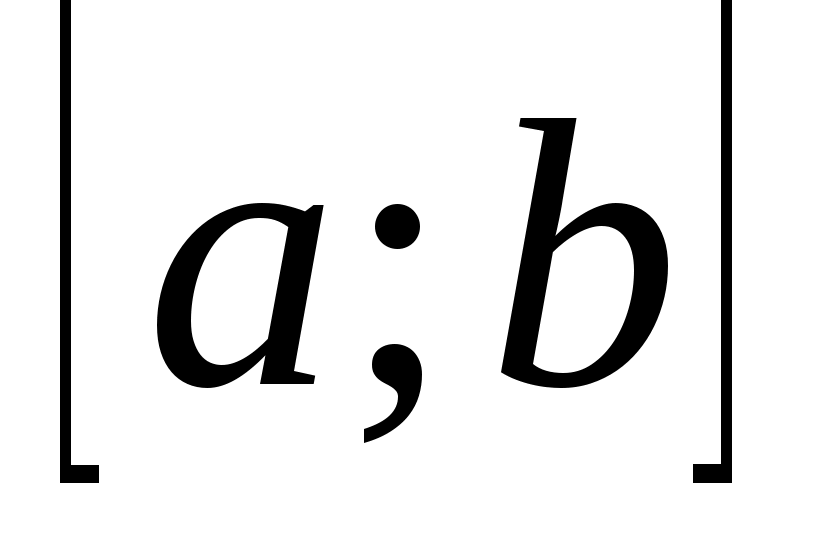 непрерывные производные до порядка непрерывные производные до порядка 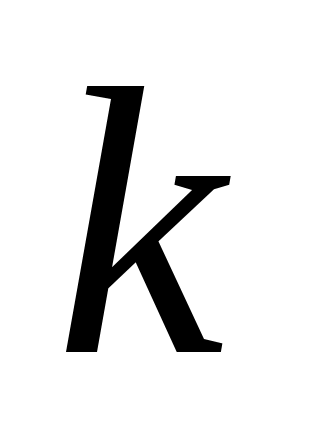 включительно; включительно;
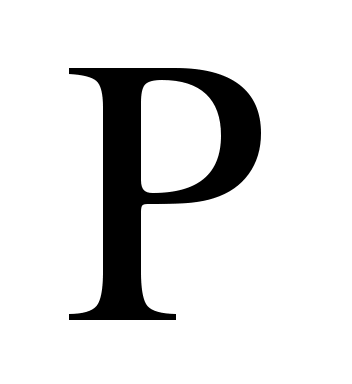 - пространство алгебраических многочленов; - пространство алгебраических многочленов;
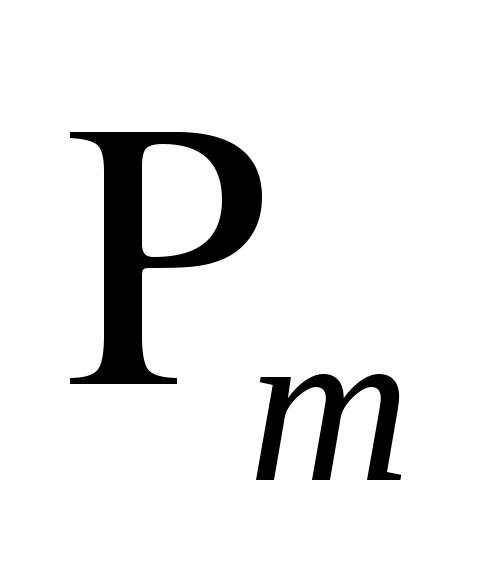 - пространство алгебраических многочленов степени не выше - пространство алгебраических многочленов степени не выше 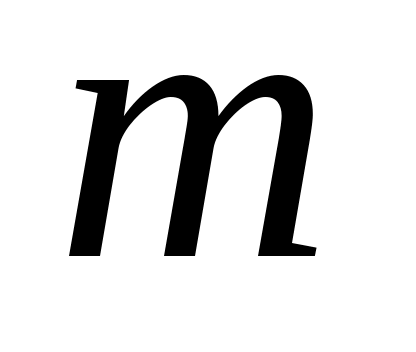 . .
I. Численное интегрирование
1.1. Постановка задачи
Пусть функция 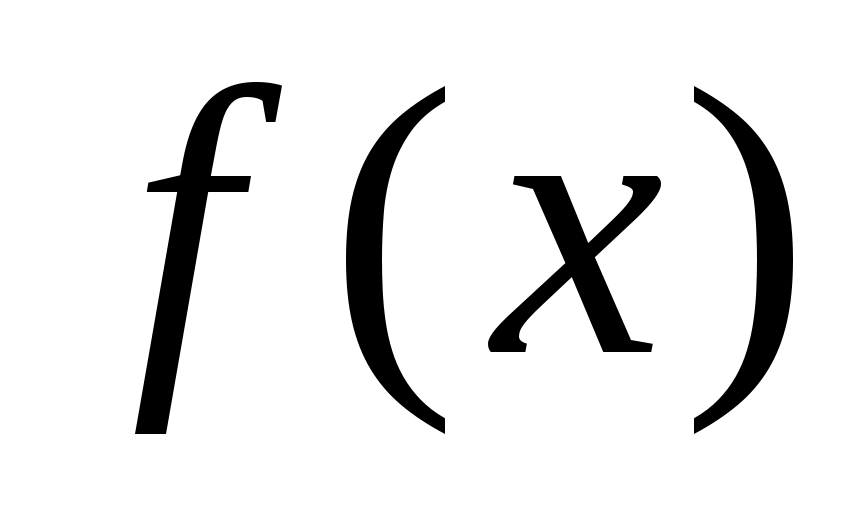 определена и непрерывна на отрезке определена и непрерывна на отрезке  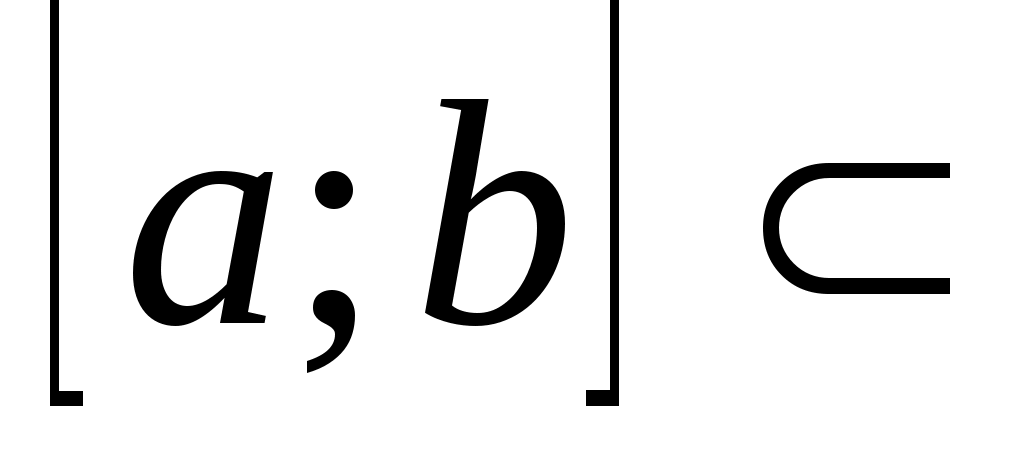 R R 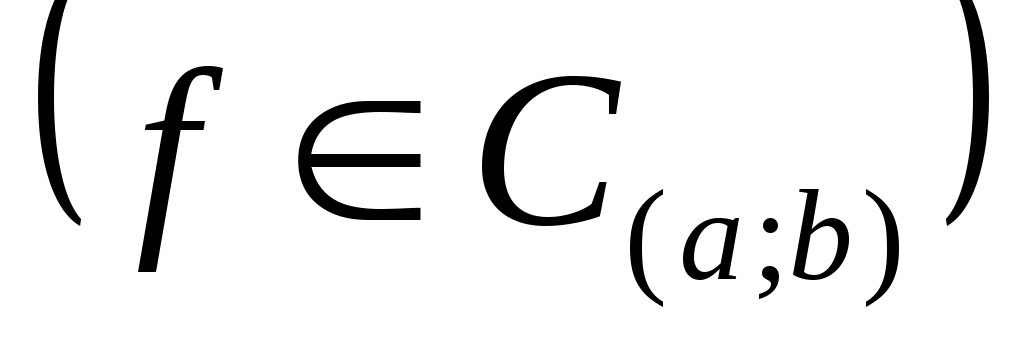 , и требуется вычислить определенный интеграл (интеграл Римана) , и требуется вычислить определенный интеграл (интеграл Римана)
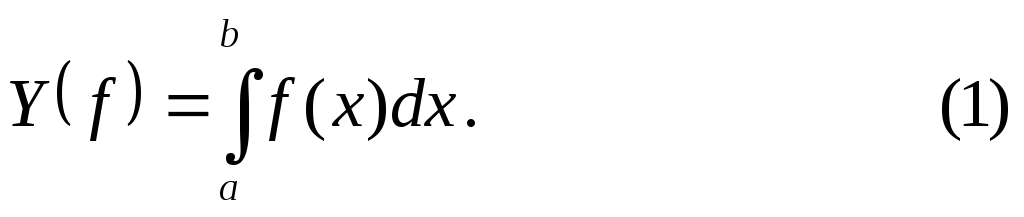 
Задачу вычисления интеграла (1) принято называть квадратурой.
Если интеграл является табличным или приводится к табличному (например, с помощью замены переменного), то он вычисляется с помощью формулы Ньютона-Лейбница
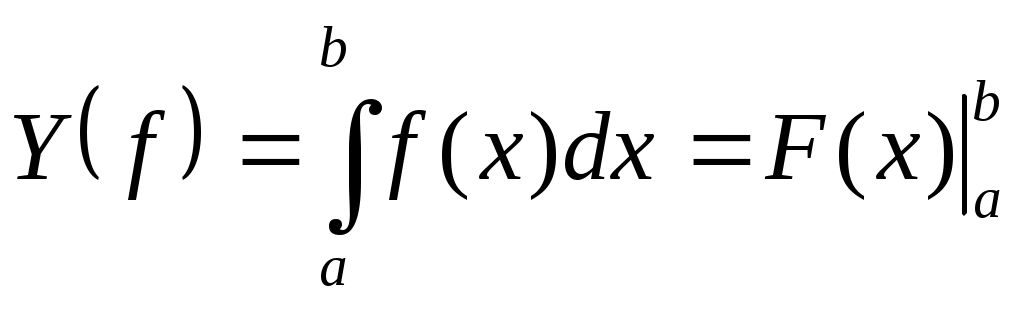 , ,
где 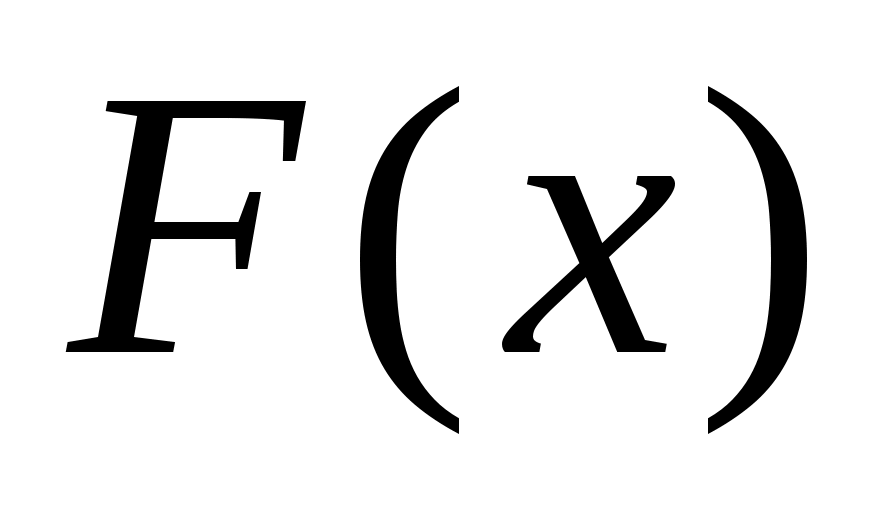 - первообразная для - первообразная для 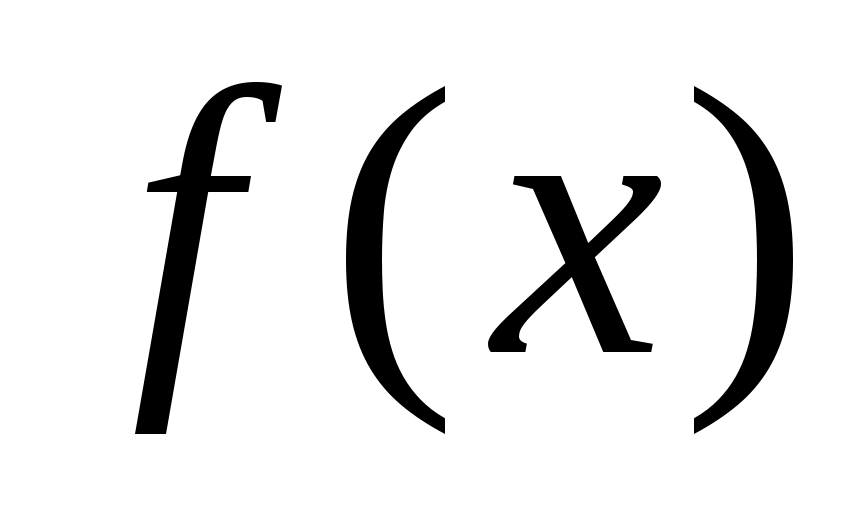 на на 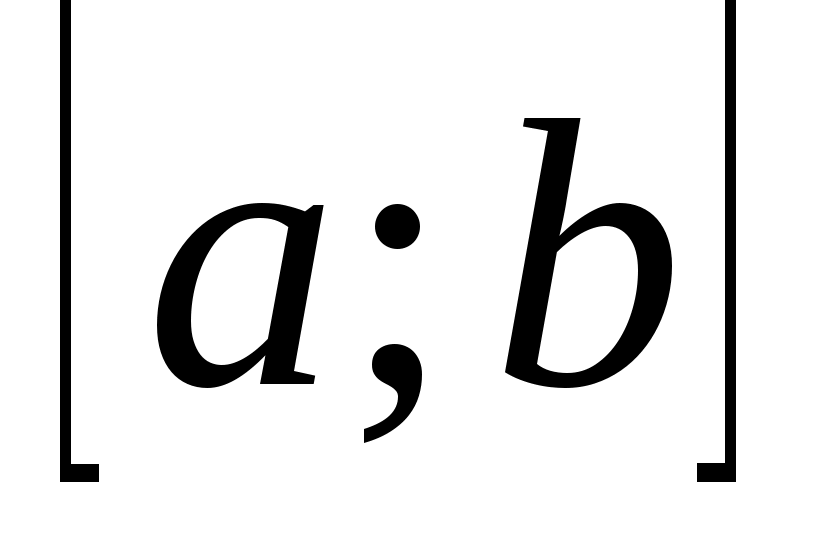 . .
На практике в редких случаях можно воспользоваться формулой Ньютона-Лейбница. Через элементарные функции выражаются первообразные только для специальных классов функций. Например, в элементарных функциях не выражаются интегралы 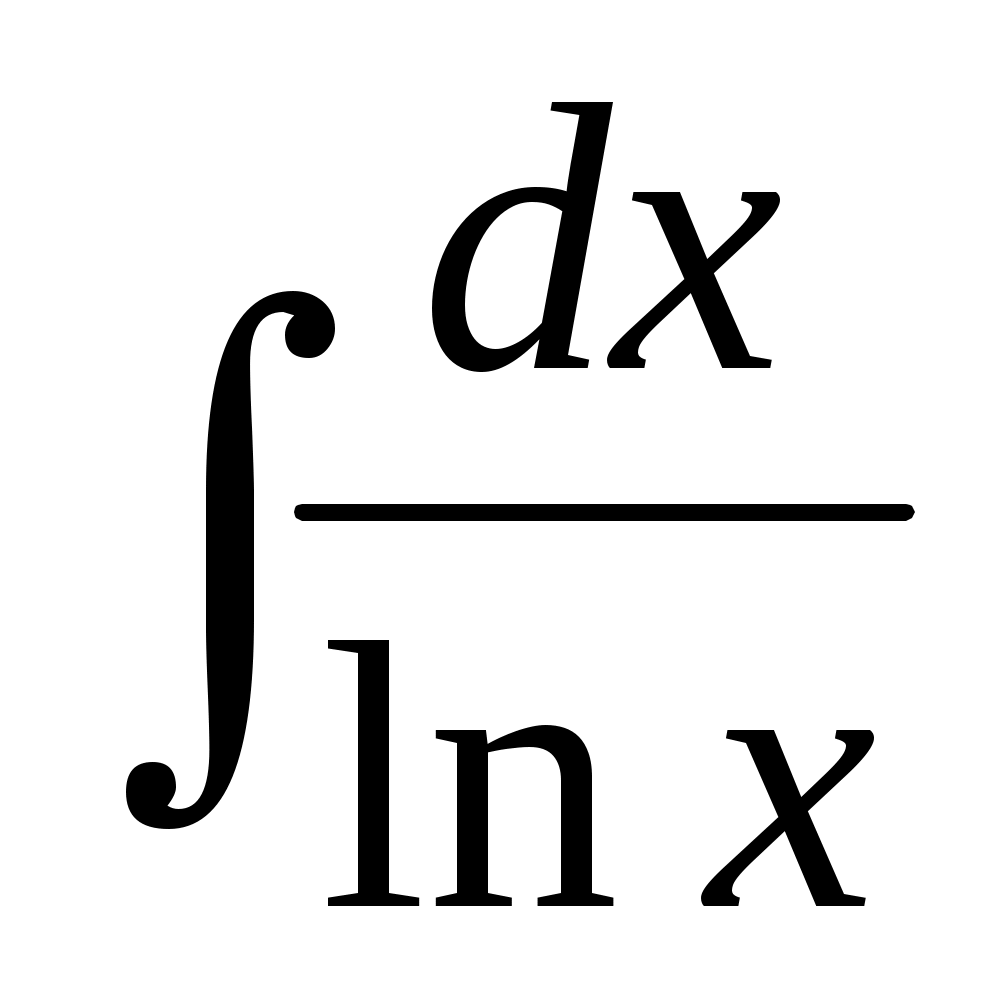 и и 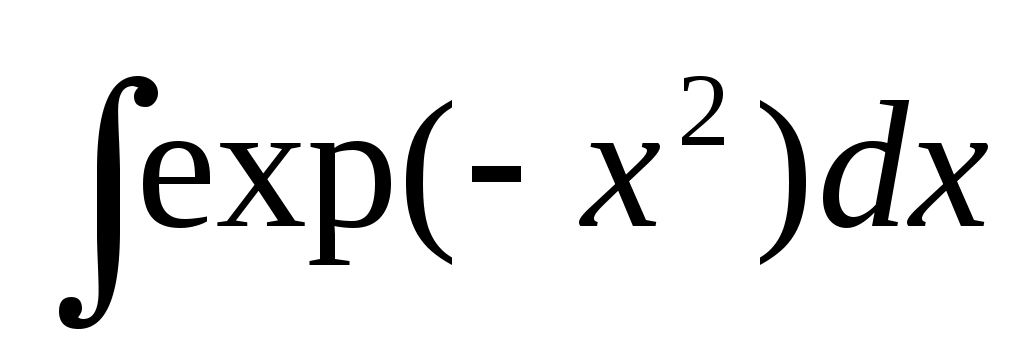 . Кроме того, функция . Кроме того, функция 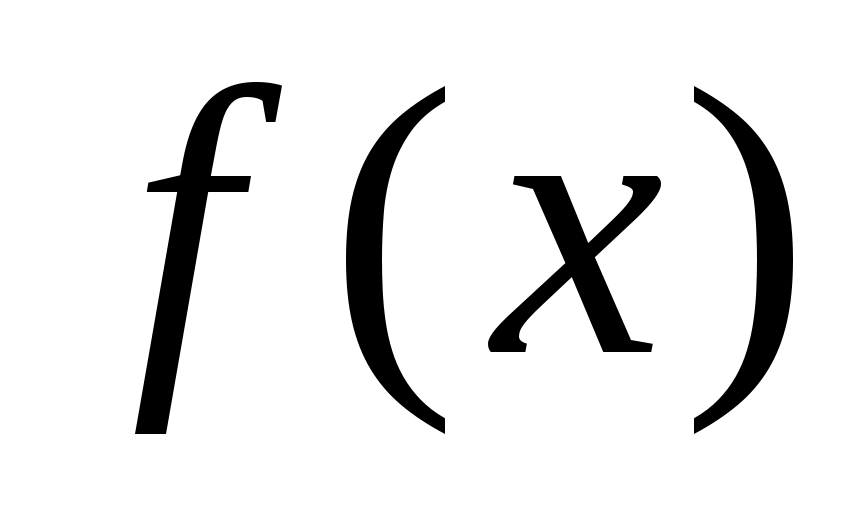 может быть задана таблично. В этом случае формула Ньютона-Лейбница вообще не применима. Поэтому приходится интеграл вычислять приближенно, используя формулы численного интегрирования. может быть задана таблично. В этом случае формула Ньютона-Лейбница вообще не применима. Поэтому приходится интеграл вычислять приближенно, используя формулы численного интегрирования.
1.2. Квадратурная формула. Квадратурный процесс
Выберем на отрезке 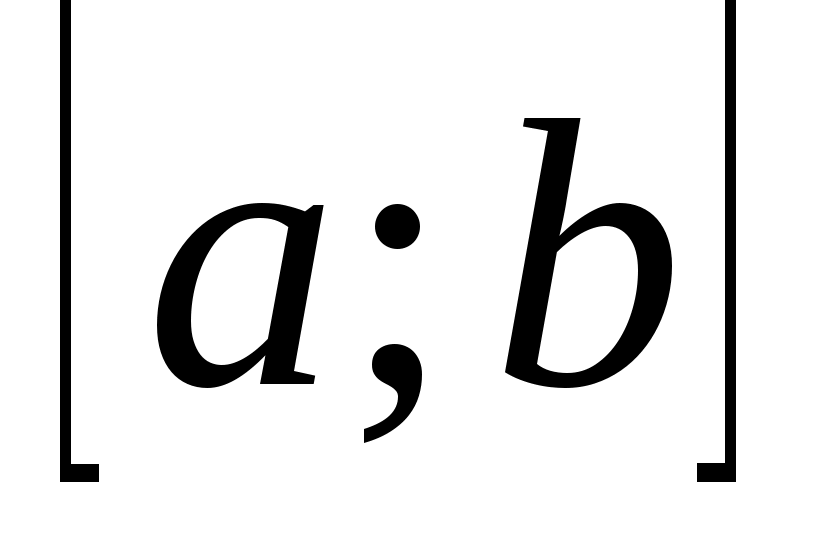 точки точки 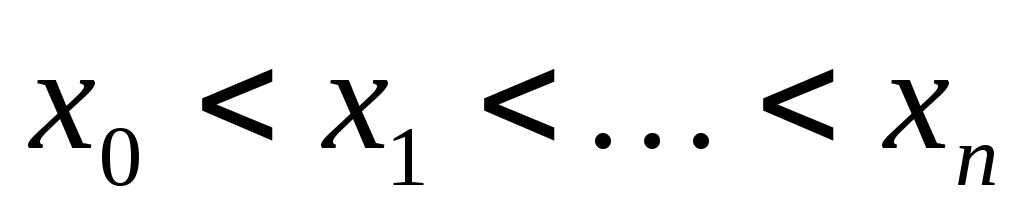 . Формула численного интегрирования . Формула численного интегрирования
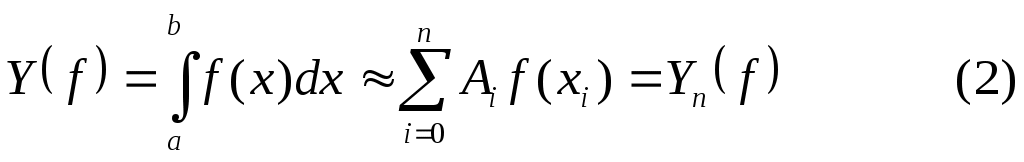
называется квадратурной. Величины 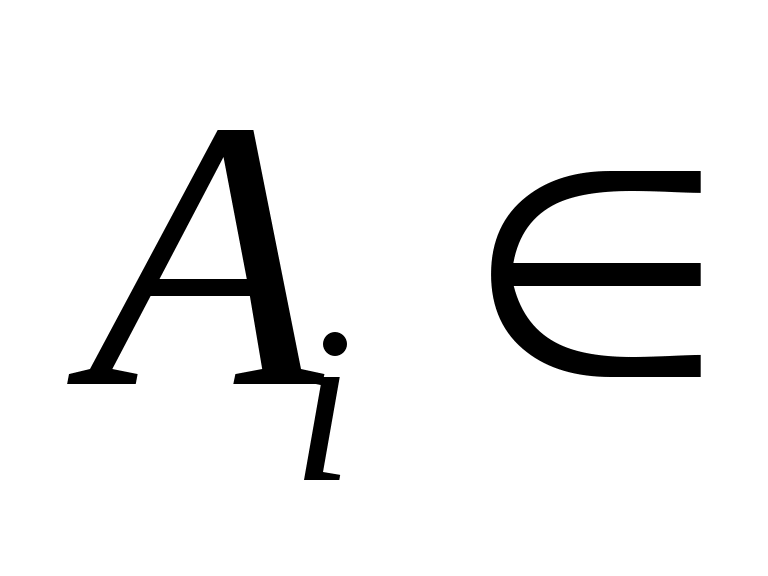 R, R,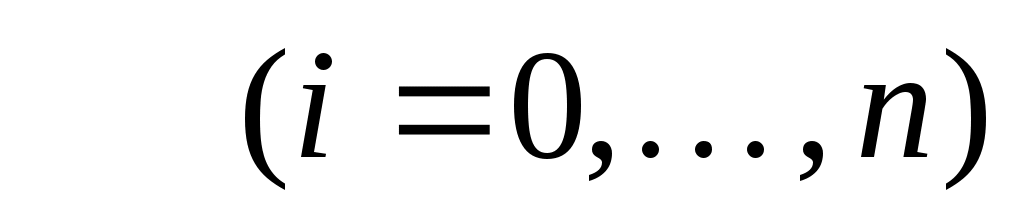 называются коэффициентами (весовыми коэффициентами) квадратурной формулы; называются коэффициентами (весовыми коэффициентами) квадратурной формулы; 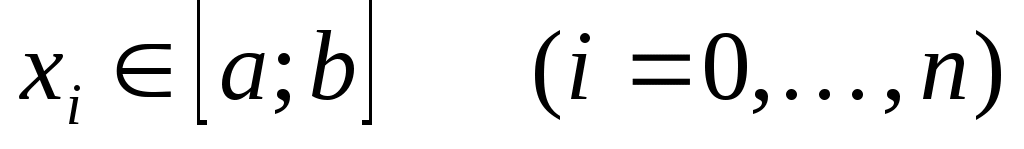 - узлами квадратурной формулы. Обычно требуют, чтобы - узлами квадратурной формулы. Обычно требуют, чтобы
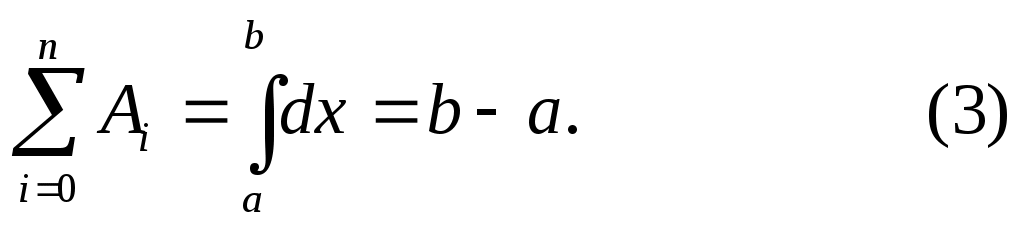
Разность
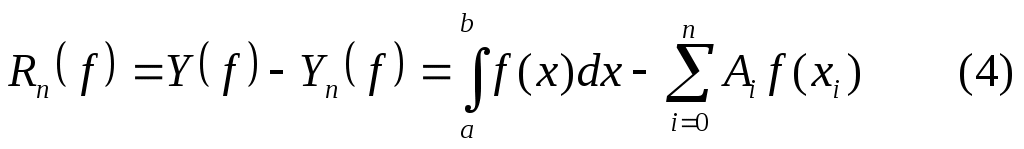
называется погрешностью (функционалом погрешности) квадратурной формулы (2).
Важно знать, для каких классов функций погрешность 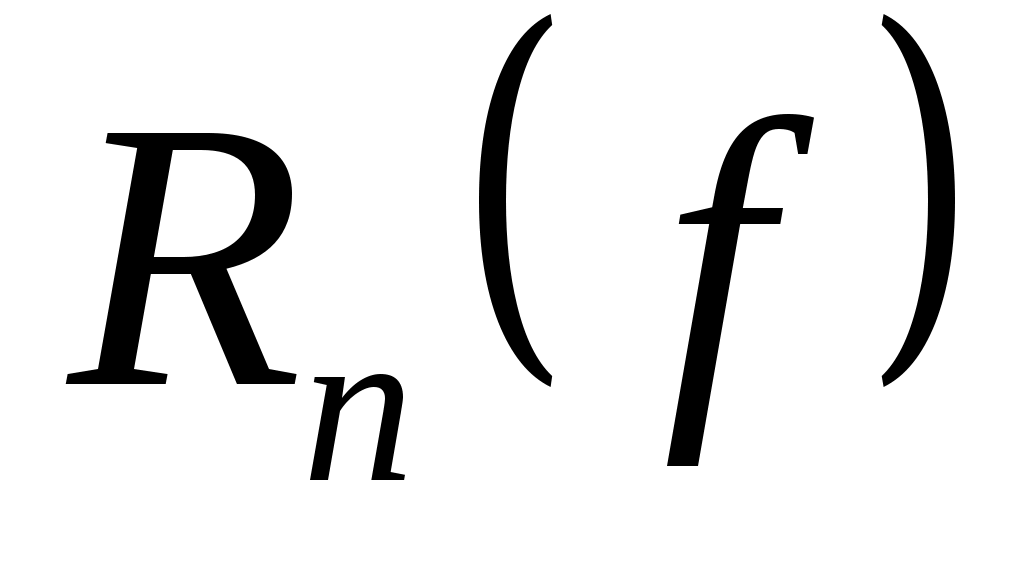 обращается в нуль. Равенство (3) означает, что квадратурная формула (2) точна на константах обращается в нуль. Равенство (3) означает, что квадратурная формула (2) точна на константах  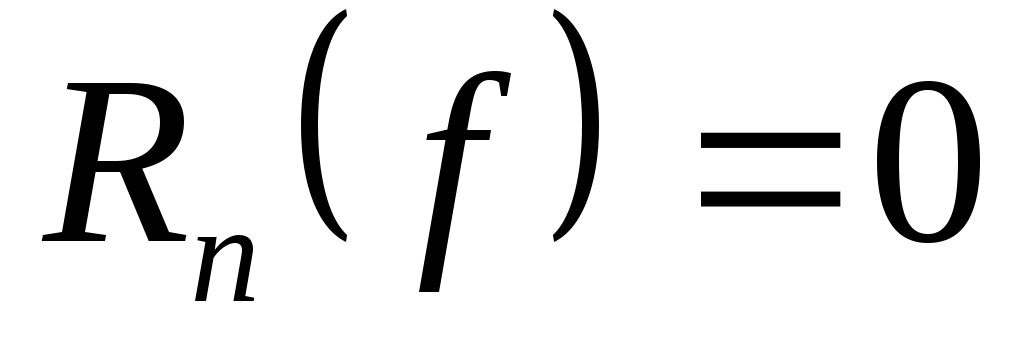 , если , если 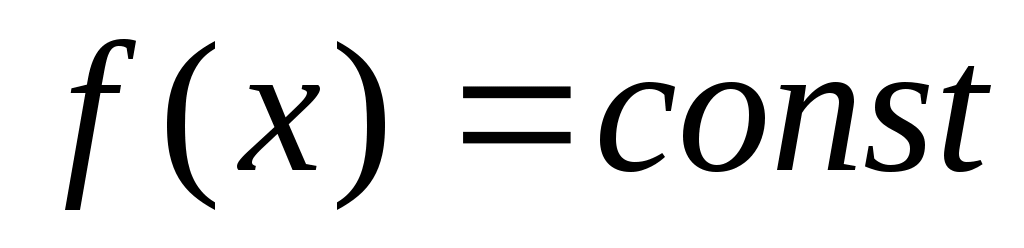 для для 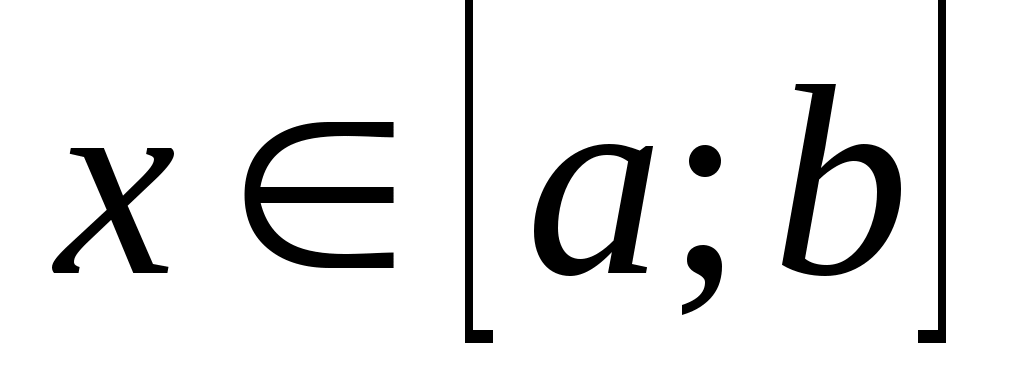 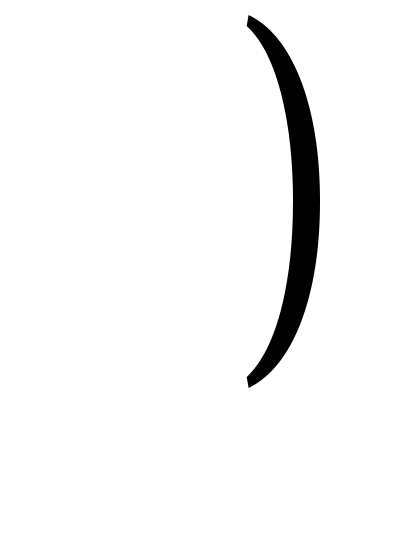 . Будем говорить, что квадратурная формула точна на многочленах степени . Будем говорить, что квадратурная формула точна на многочленах степени 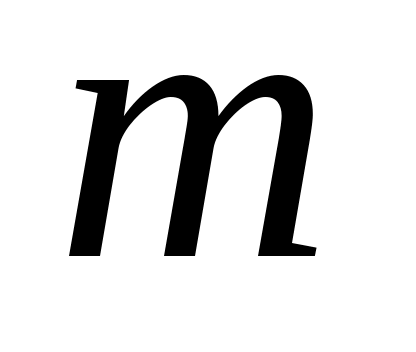 , если , если 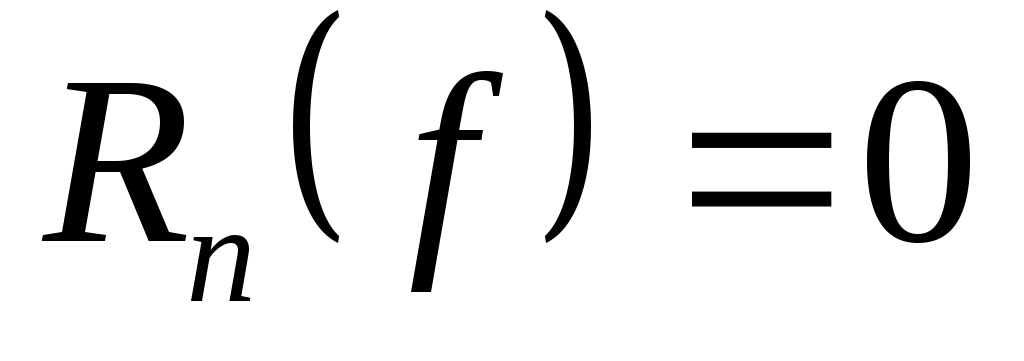 для любой функции для любой функции 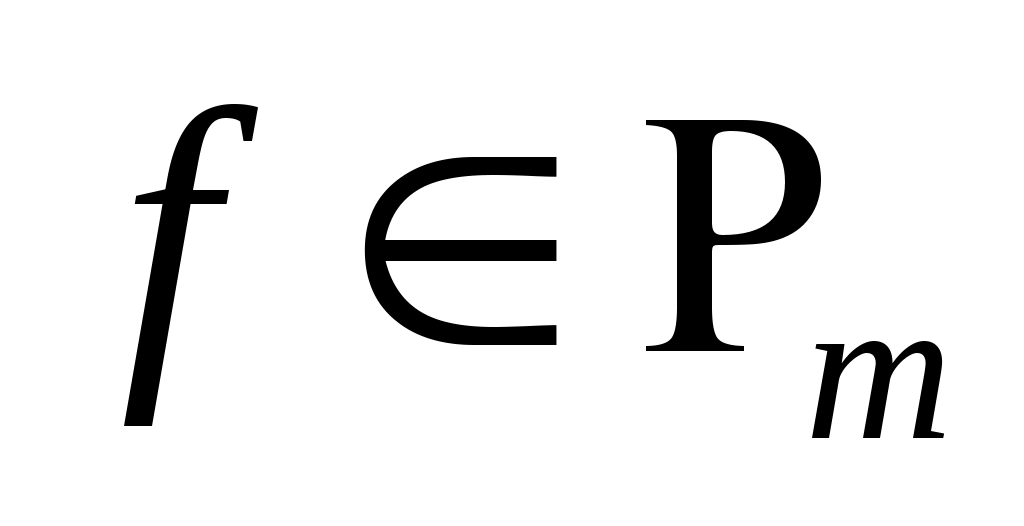 , где , где 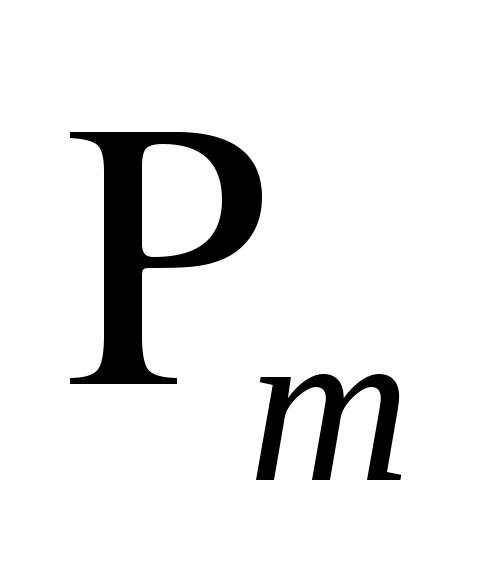 - пространство многочленов степени не выше - пространство многочленов степени не выше 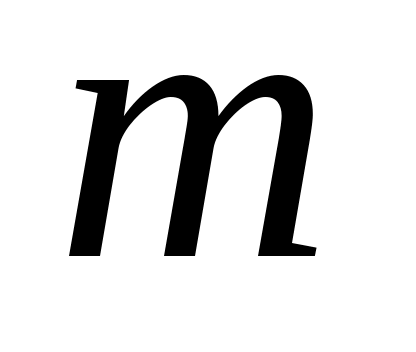 . .
Квадратурная формула (2) содержит 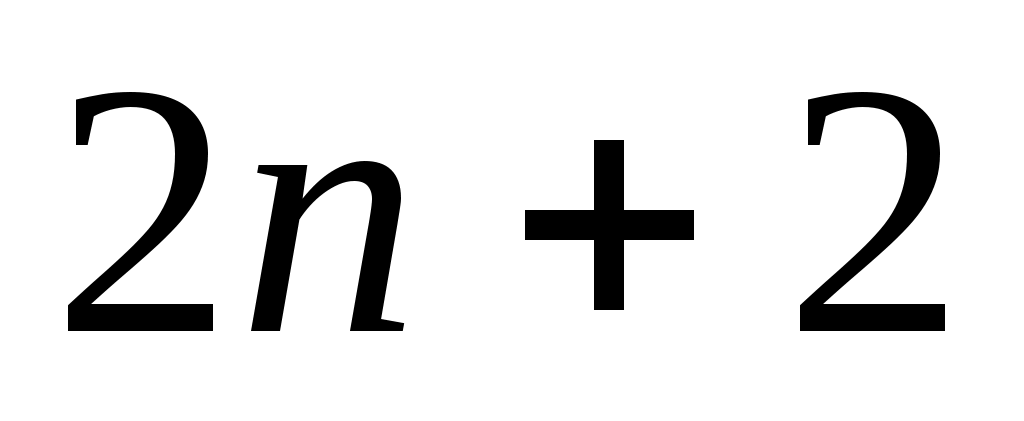 параметров: параметров: 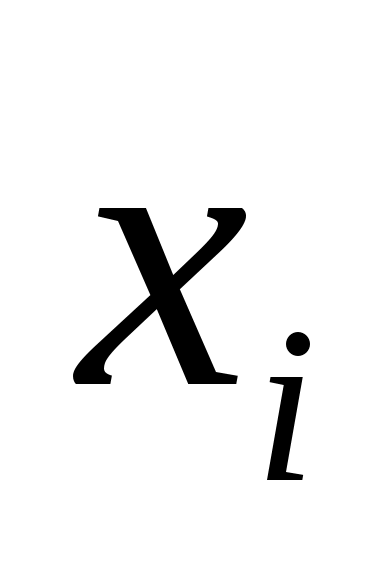 и и 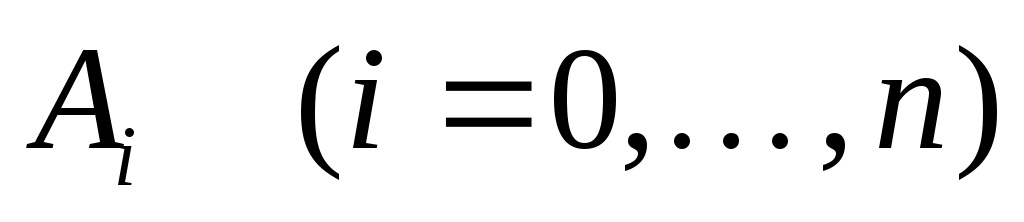 . Если для каждого . Если для каждого 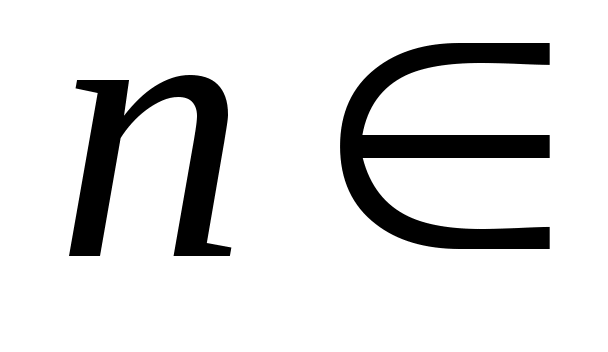 N выбрать свои узлы N выбрать свои узлы 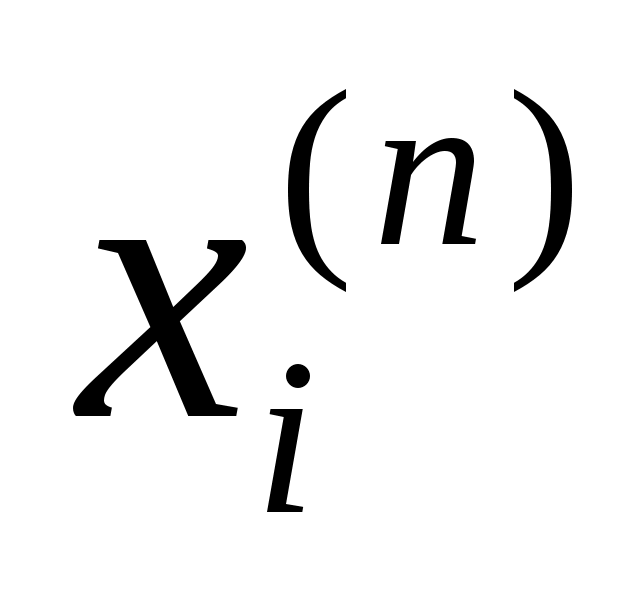 и коэффициенты и коэффициенты 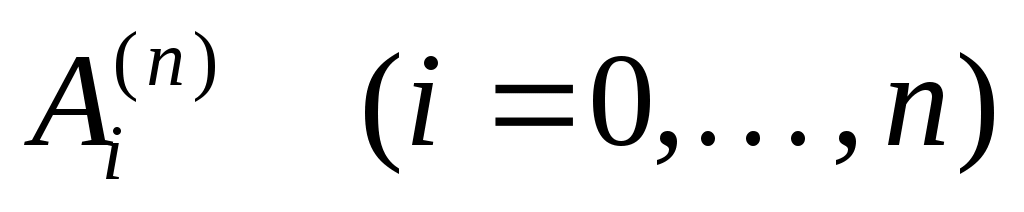 , то получим квадратурный процесс: , то получим квадратурный процесс:
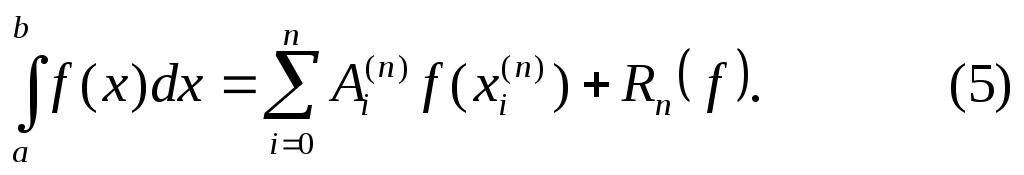
Квадратурный процесс (5) называется сходящимся, если для любой функции 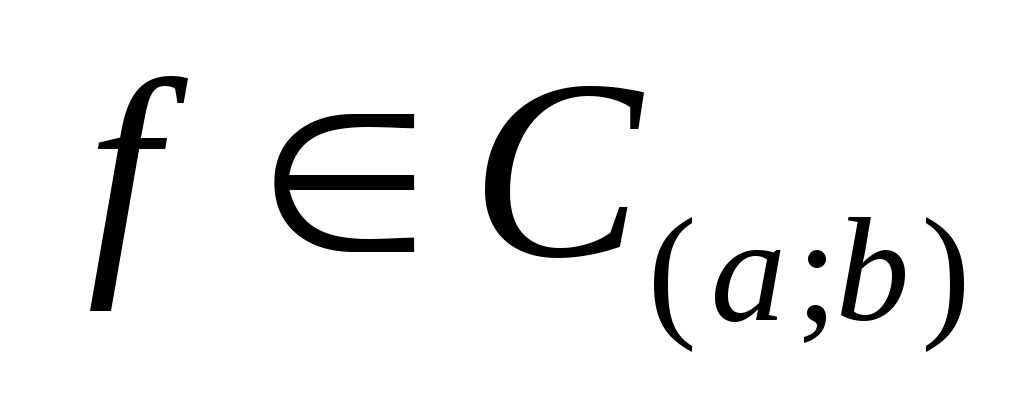 погрешность квадратурной формулы погрешность квадратурной формулы 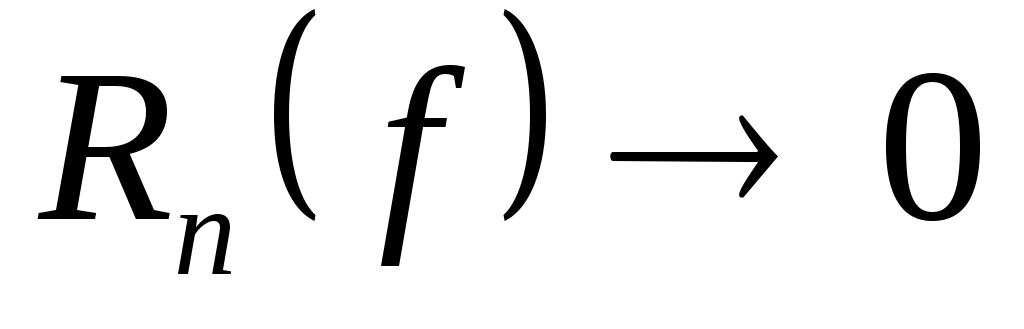 при при  . Это означает, что последовательность функционалов погрешности . Это означает, что последовательность функционалов погрешности 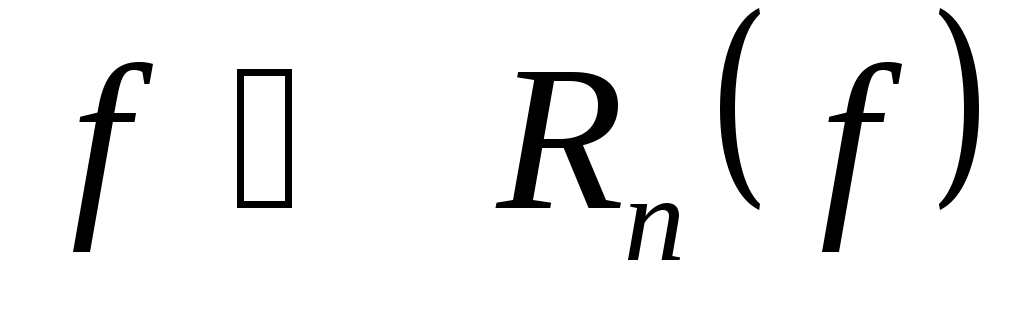 сходится к нулю на каждом элементе сходится к нулю на каждом элементе 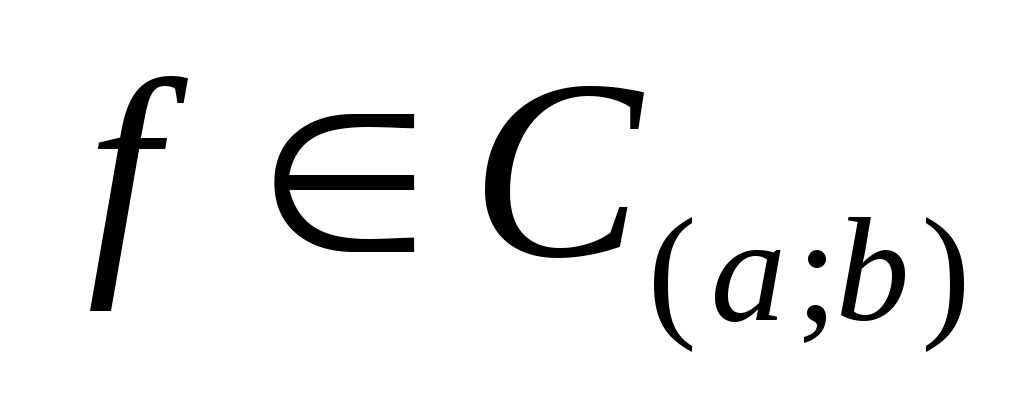 (см. [4], стр. 165). (см. [4], стр. 165).
Замечание 1. 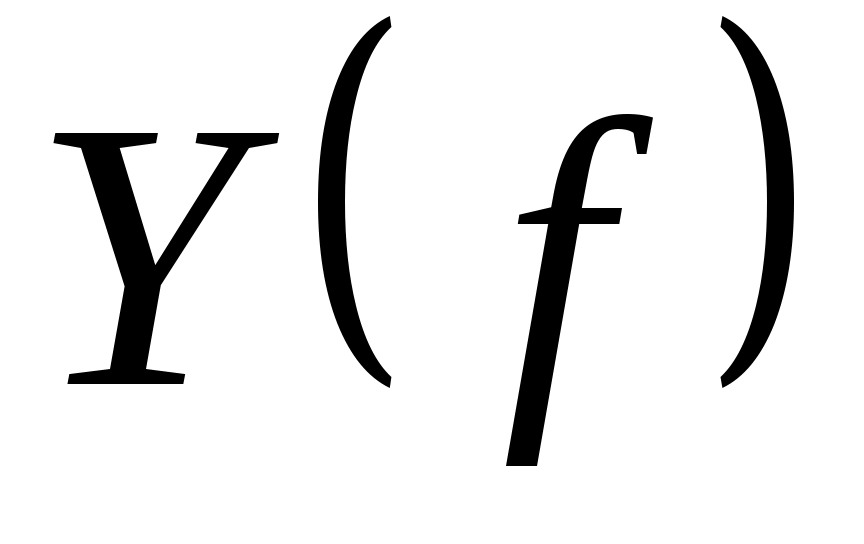 , ,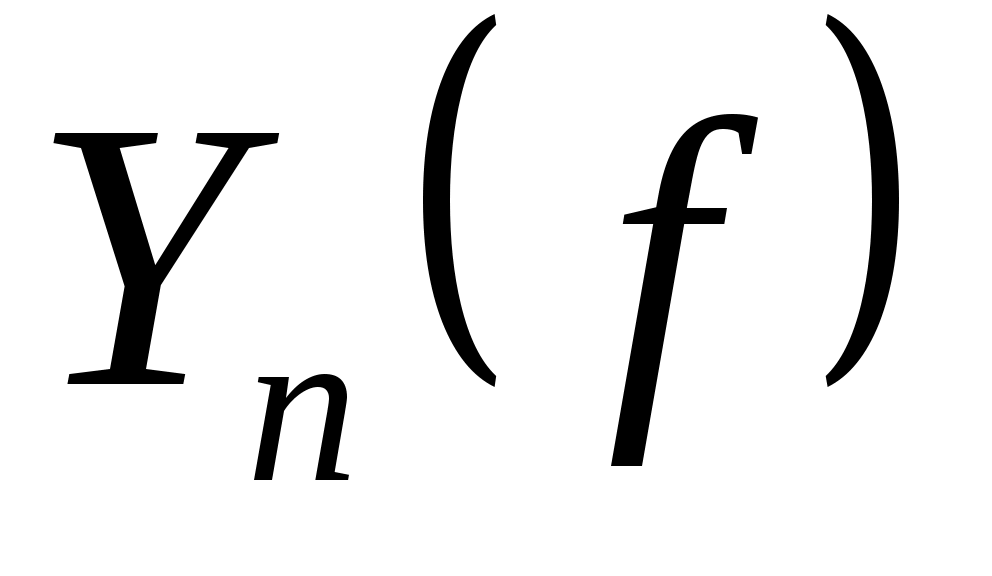 , ,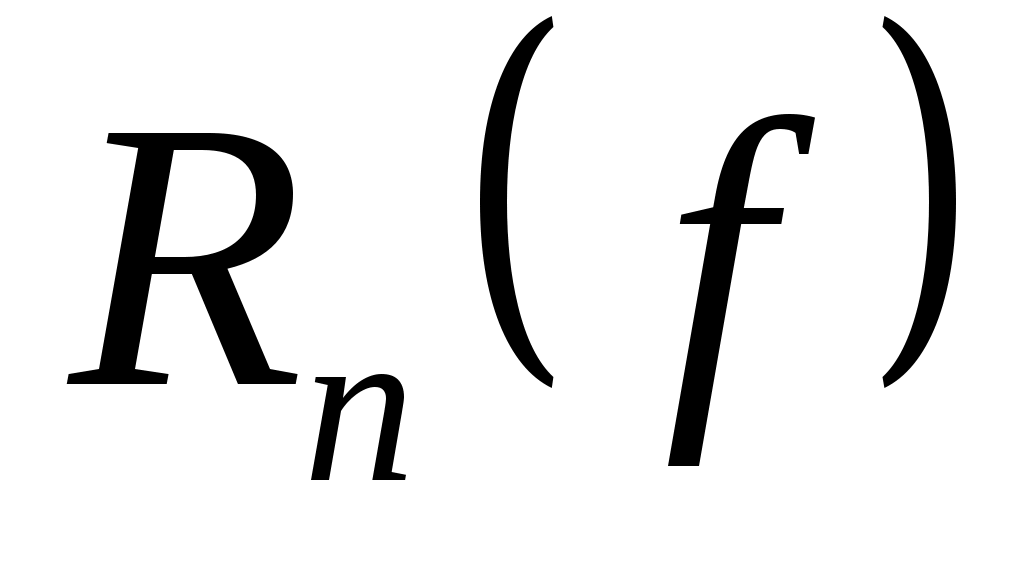 являются линейными непрерывными (ограниченными) функционалами на являются линейными непрерывными (ограниченными) функционалами на 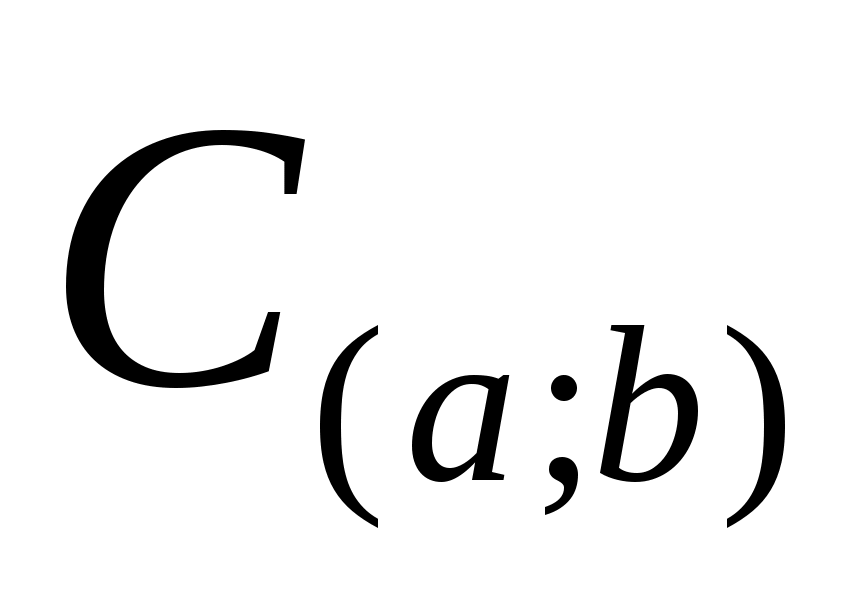 : :
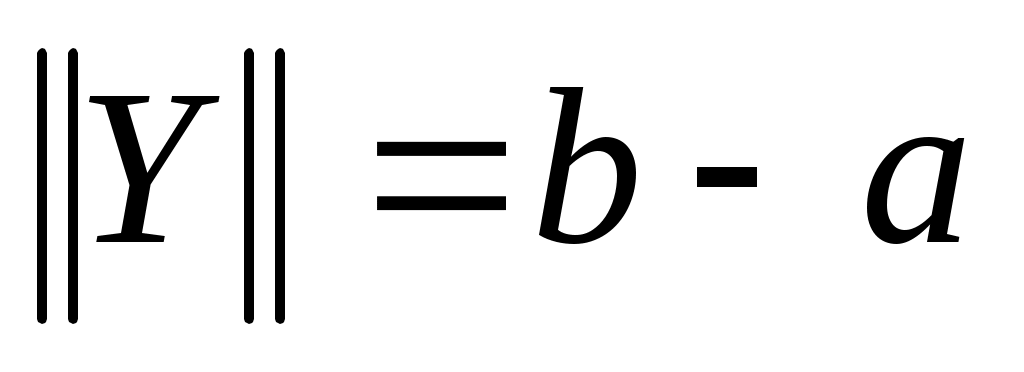 , , 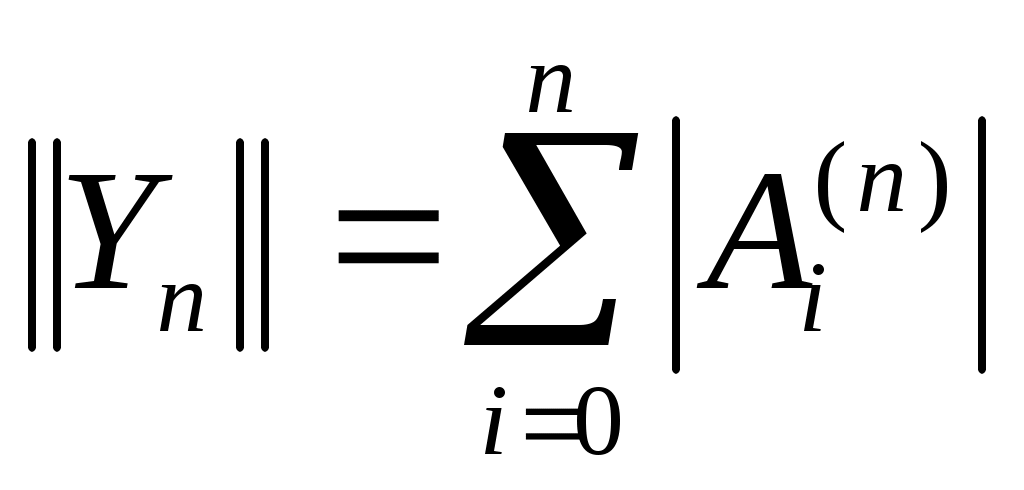 , , 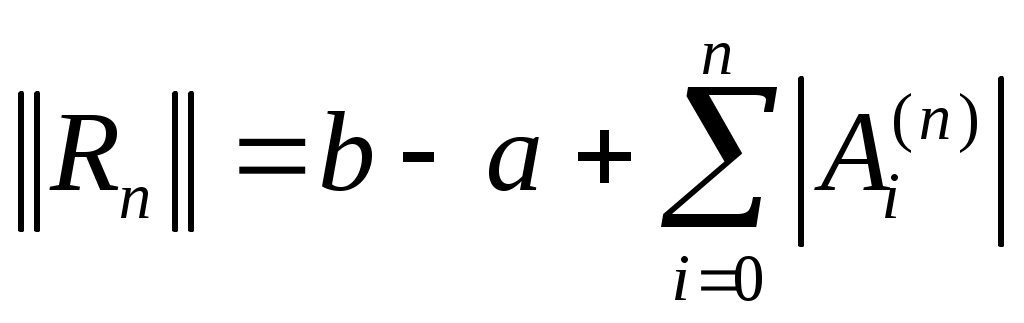 . .
Из последнего равенства следует, что последовательность функционалов погрешности не может равномерно сходиться к нулю 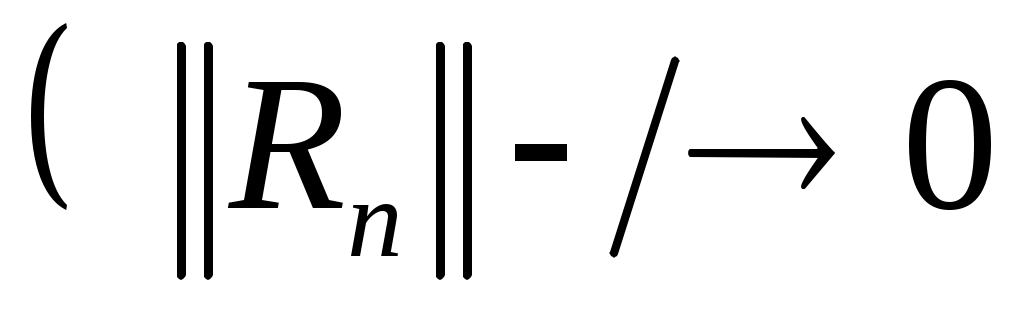 при при 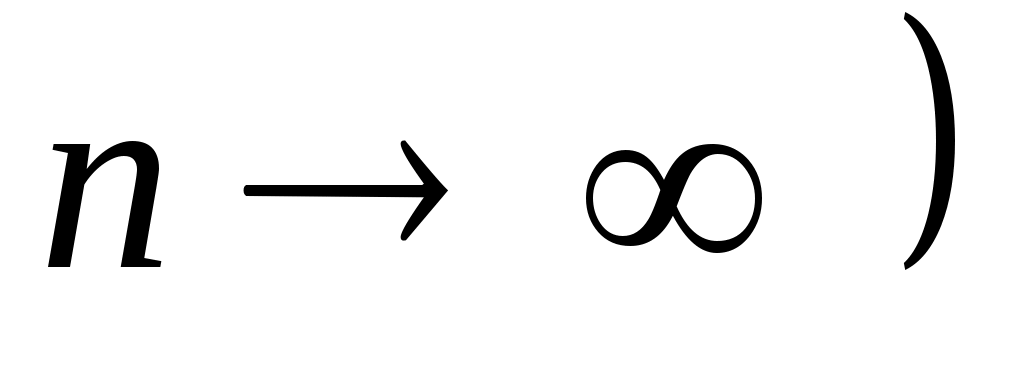 . .
Из теоремы Банаха-Штейнгауса (см. [4], с. 134, с. 166) немедленно получаем условие сходимости квадратурного процесса:
Теорема 1. Для того чтобы квадратурный процесс (5) сходился, необходимо и достаточно выполнение следующих двух условий:
1) 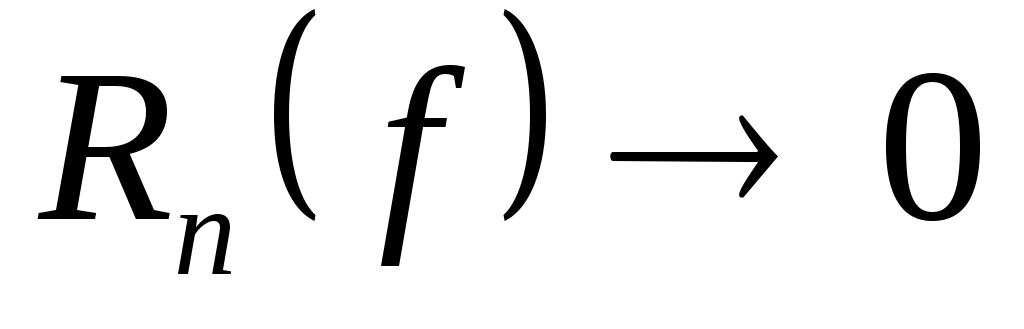 при при  для любой функции для любой функции 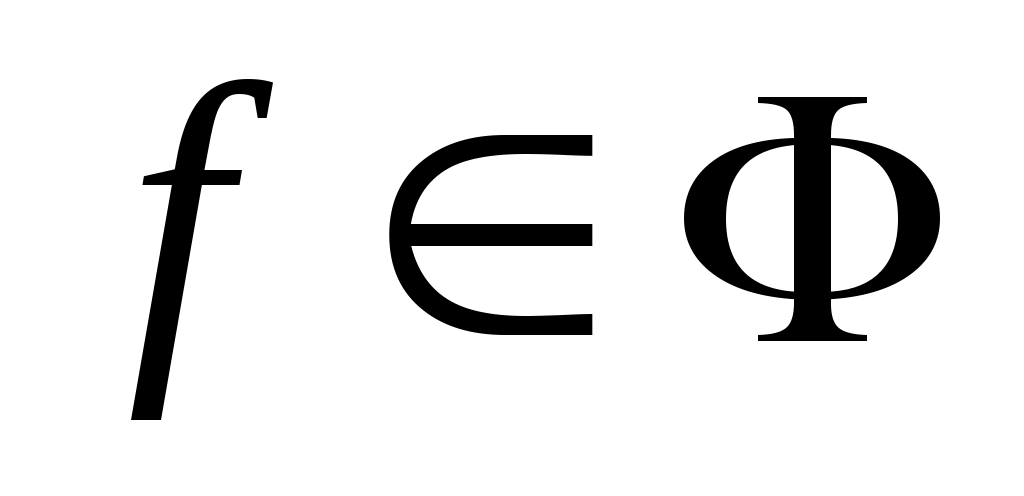 , где , где 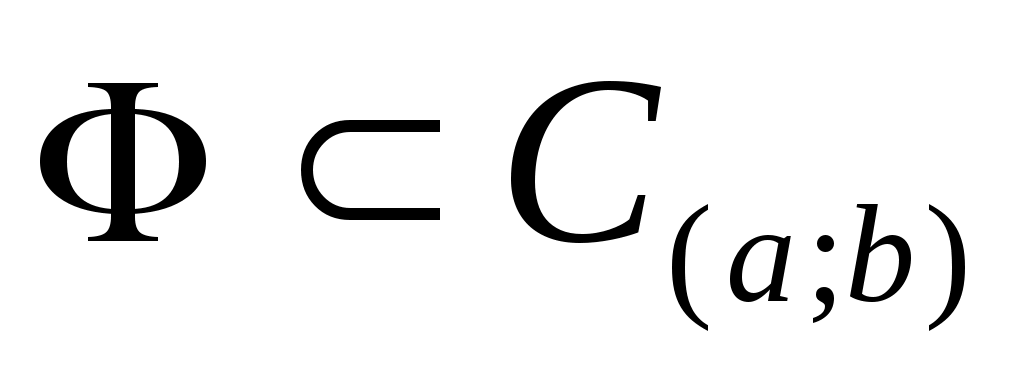 - множество, линейные комбинации элементов которого лежат всюду плотно в - множество, линейные комбинации элементов которого лежат всюду плотно в 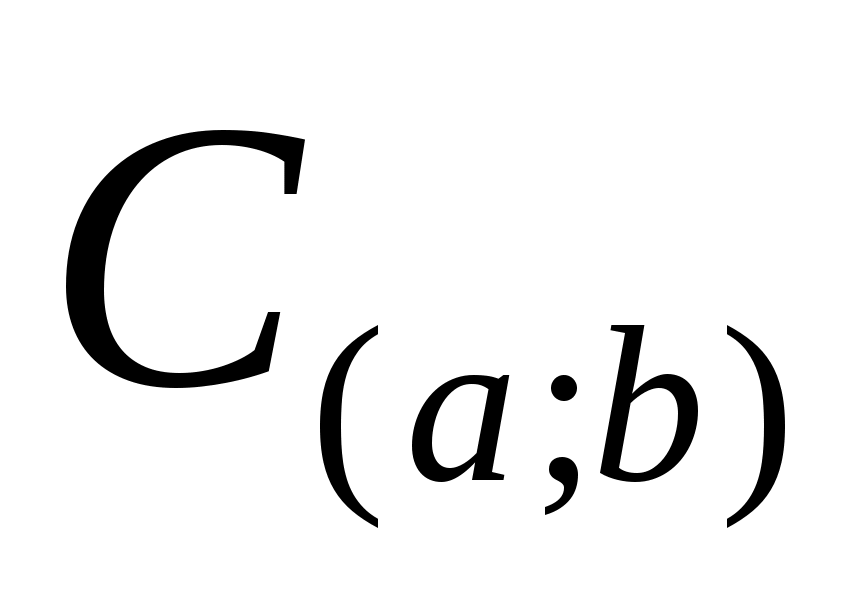 ; ;
2) существует константа 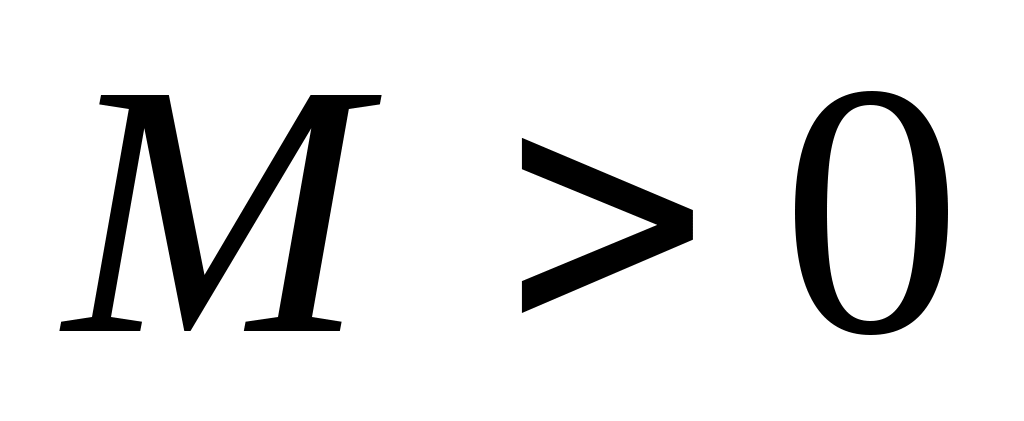 такая, что такая, что 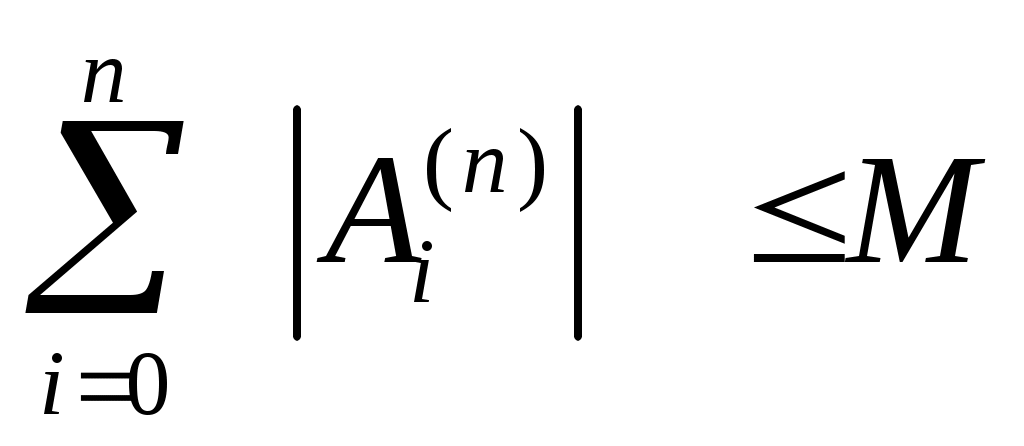 для всех для всех 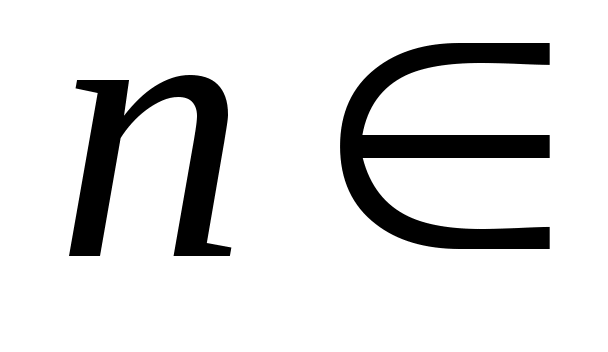 N. N.
1.3. Интерполяционная квадратурная формула
Пусть заданы узлы 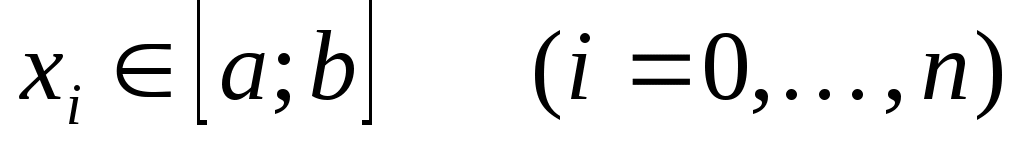 квадратурной формулы (2). По подинтегральной функции квадратурной формулы (2). По подинтегральной функции 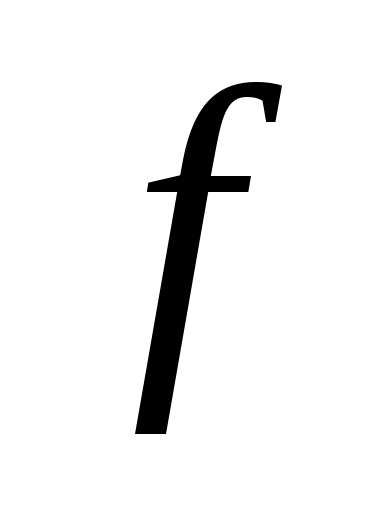 и узлам и узлам 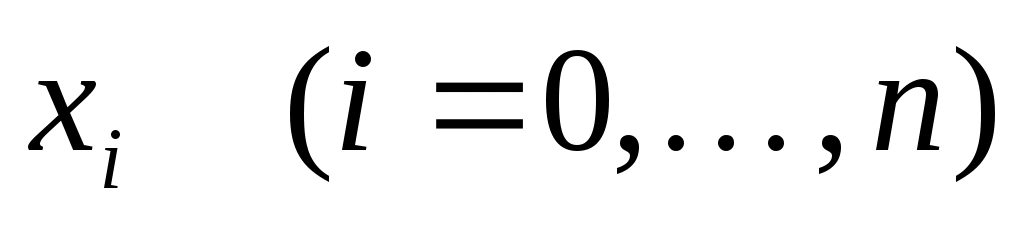 построим интерполяционный многочлен Лагранжа построим интерполяционный многочлен Лагранжа
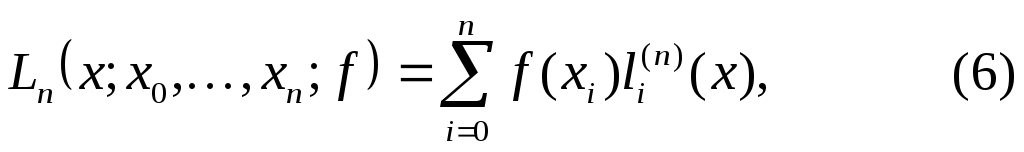
где 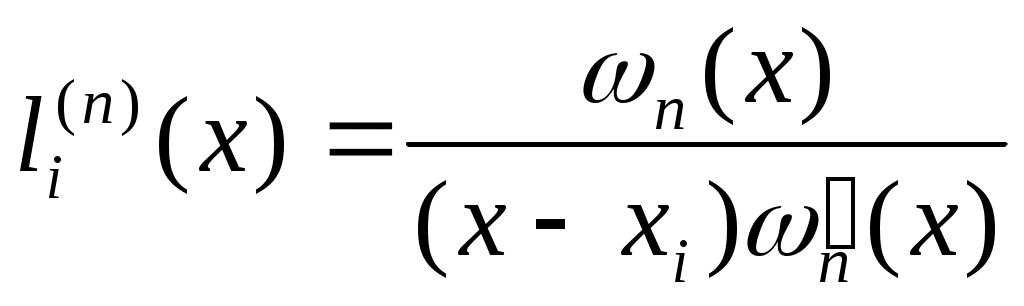 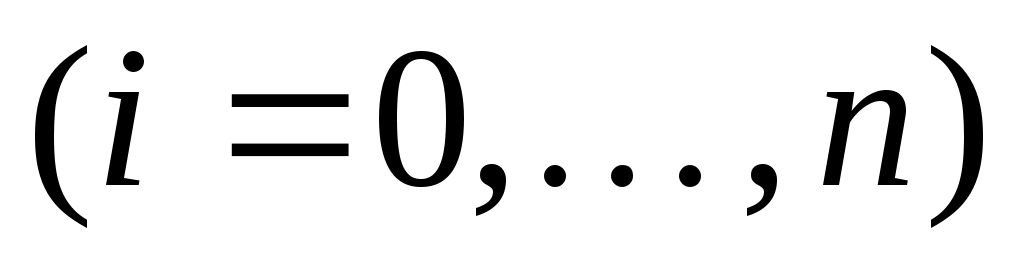 , , 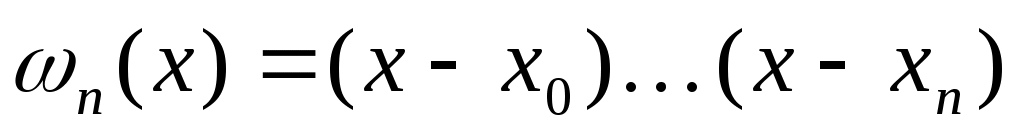 . .
Положив
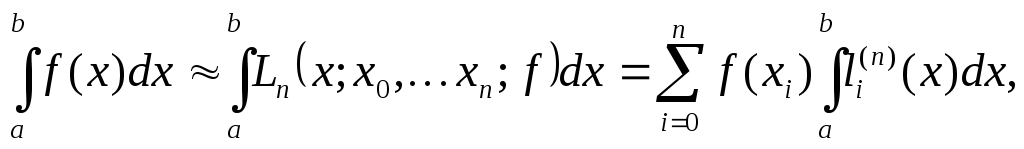
получим интерполяционную квадратурную формулу
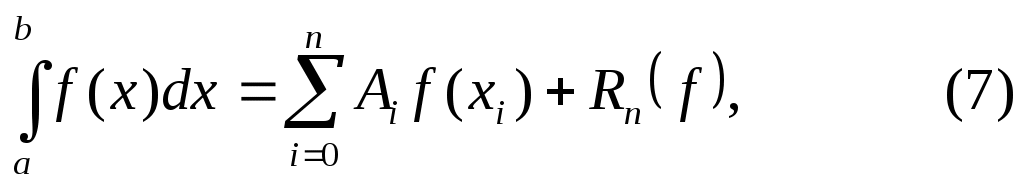
где
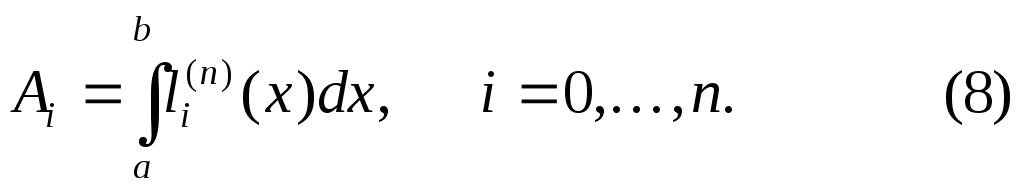
Таким образом, квадратурная формула (2) является интерполяционной, если её коэффициенты вычисляются по формуле (8).
Замечание 2. Коэффициенты интерполяционной квадратурной формулы зависят только от узлов 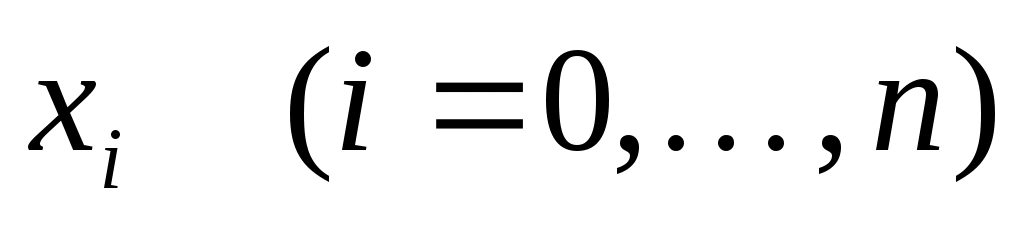 и не зависят от подинтегральной функции и не зависят от подинтегральной функции 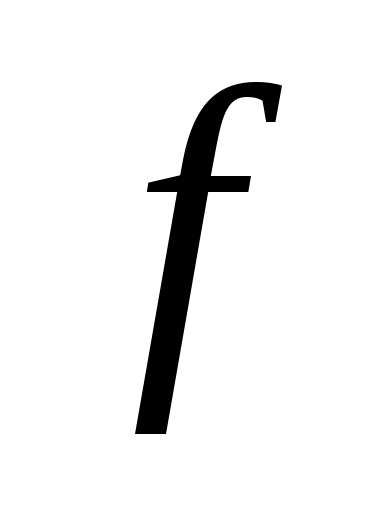 . .
Интерполяционная квадратурная формула (7)–(8) точна на многочленах степени 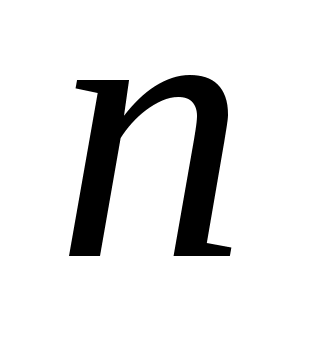 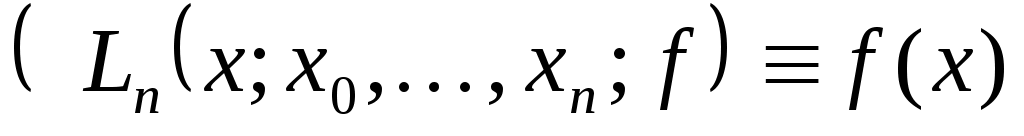 , если , если  . Очевидно, что если квадратурная формула (2) с . Очевидно, что если квадратурная формула (2) с 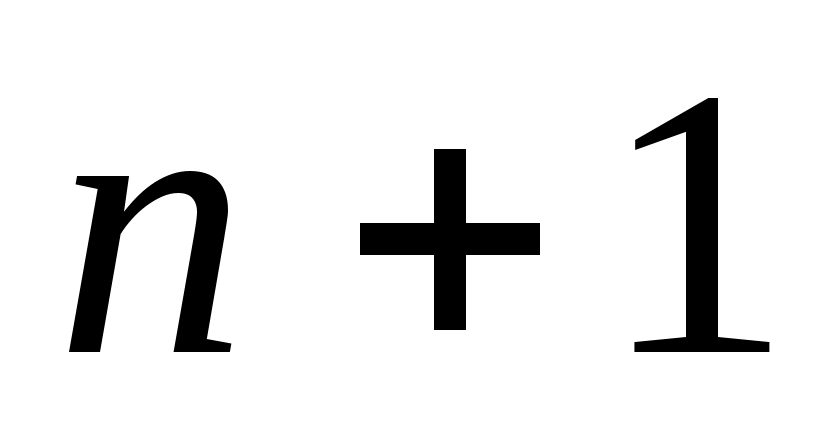 узлами имеет алгебраический порядок точности не ниже узлами имеет алгебраический порядок точности не ниже 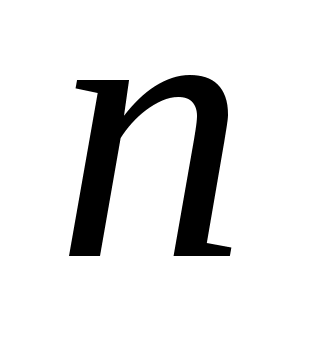 , то она является интерполяционной. , то она является интерполяционной.
Погрешность интерполяционной квадратурной формулы (7)–(8) имеет вид
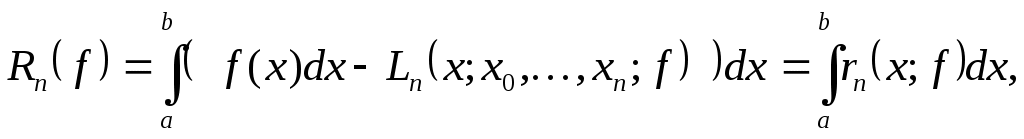
где 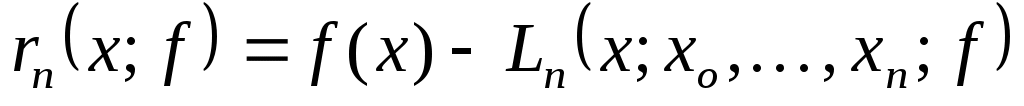 - погрешность интерполяции. - погрешность интерполяции.
Если 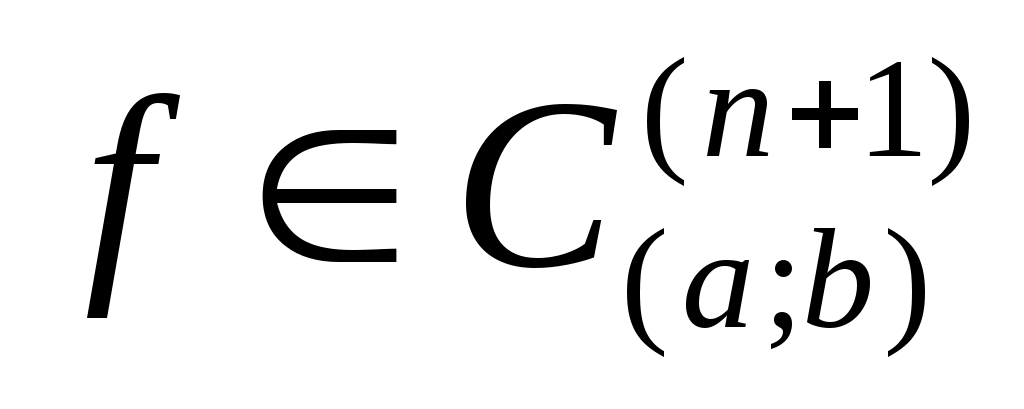 , то , то
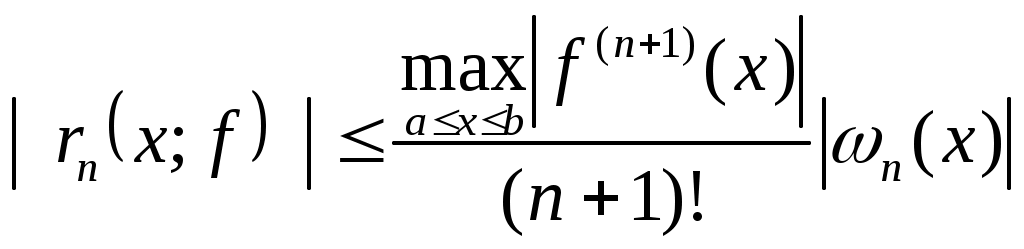
и, следовательно,
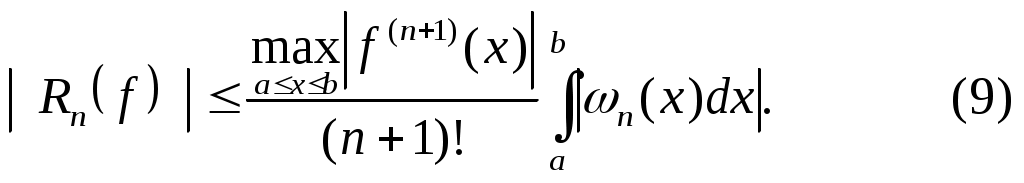
Часто оценку (9) заменяют более грубой
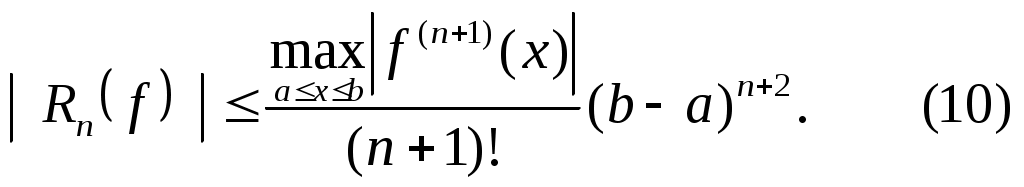
Теорема 2. Для сходимости квадратурного процесса (5), порожденного интерполяционной квадратурной формулой (7)-(8) с таблицей узлов  : :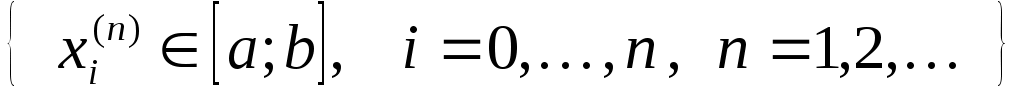 , необходимо и достаточно, чтобы , необходимо и достаточно, чтобы 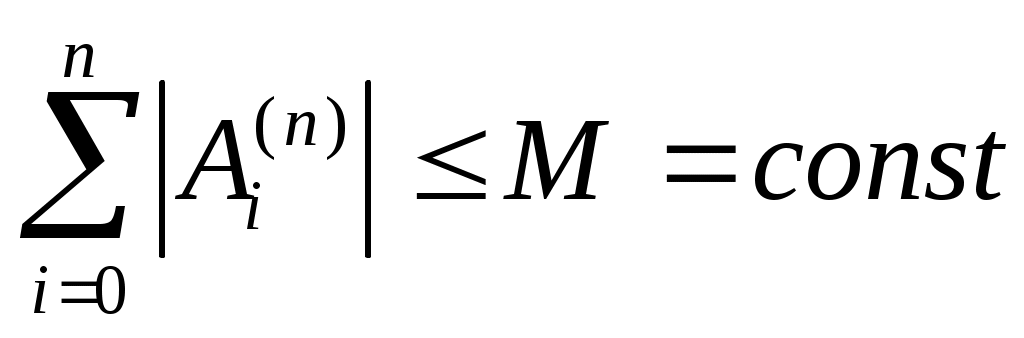 для любого для любого 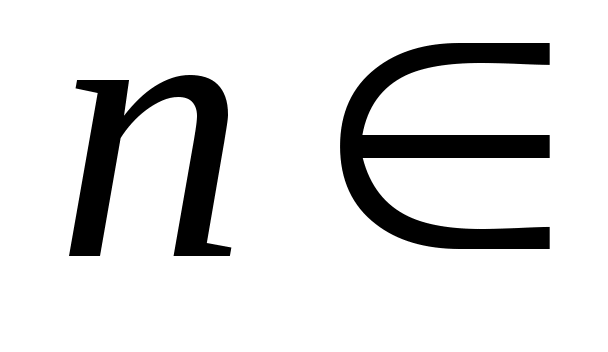 N. N.
Действительно, для всякого многочлена 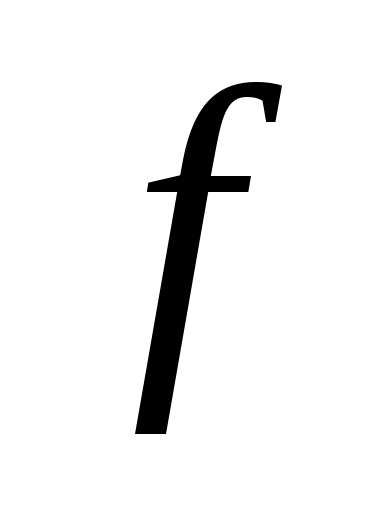 степени степени 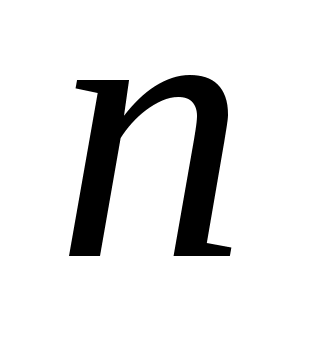 имеем при имеем при 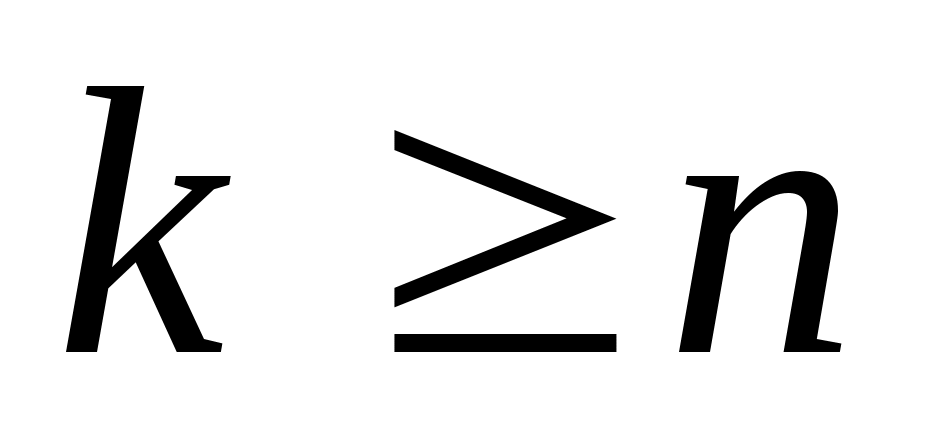 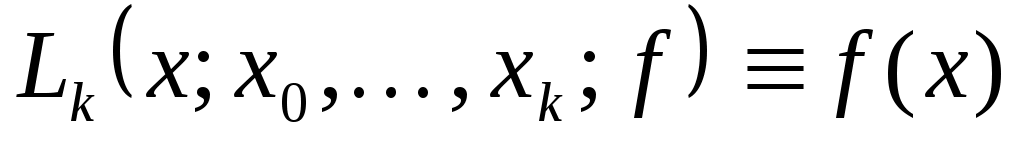 и, следовательно, и, следовательно, 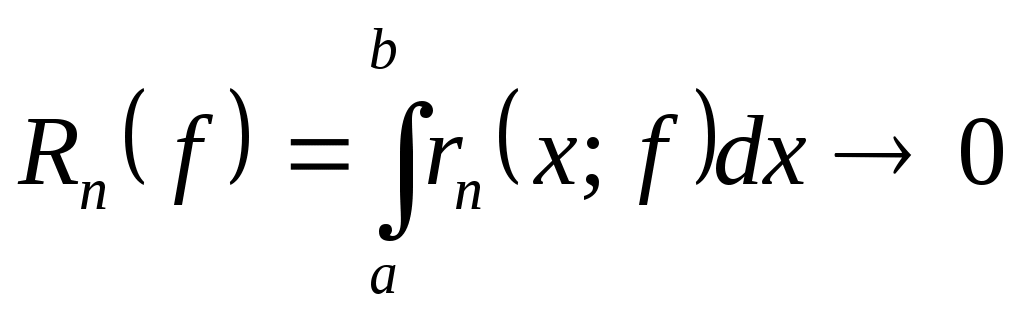 при при  для любой функции для любой функции 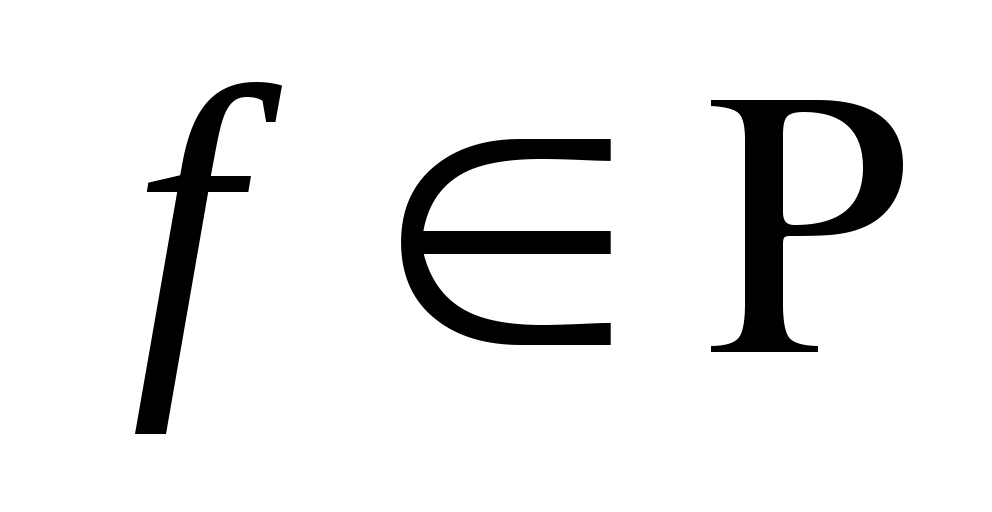 , где , где 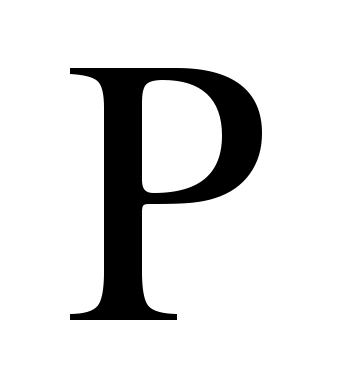 - пространство многочленов, всюду плотное в - пространство многочленов, всюду плотное в 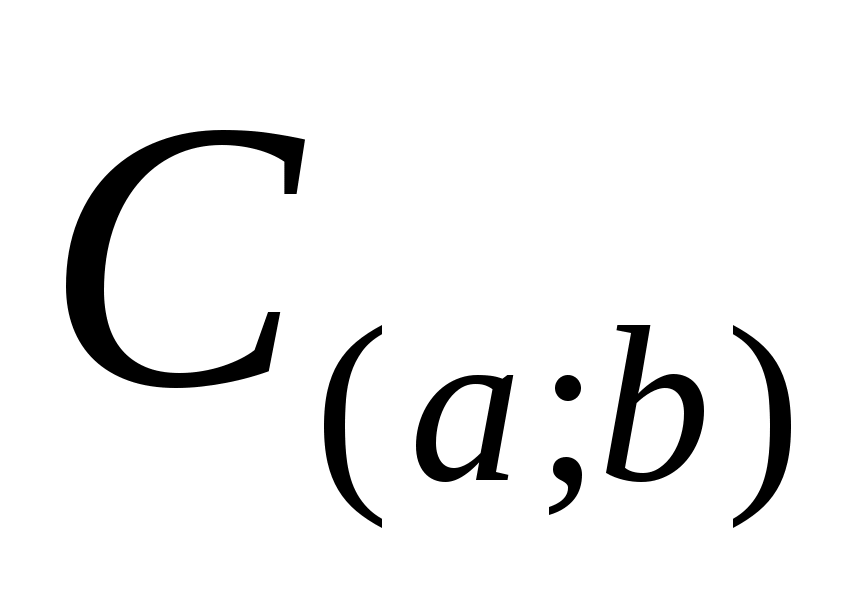 . Утверждение теоремы 2 теперь немедленно следует из теоремы 1. . Утверждение теоремы 2 теперь немедленно следует из теоремы 1.
Для любой таблицы узлов  : :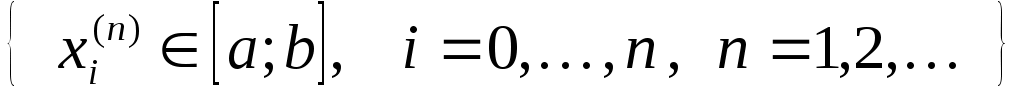 , используя формулу (8), получаем , используя формулу (8), получаем
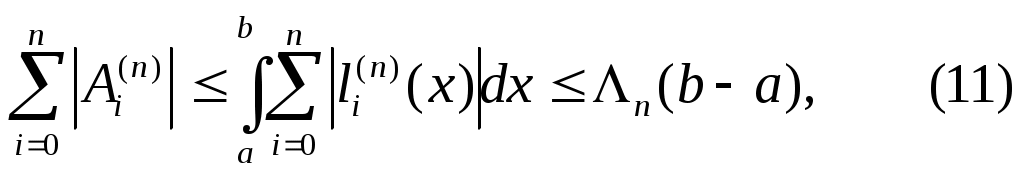
где 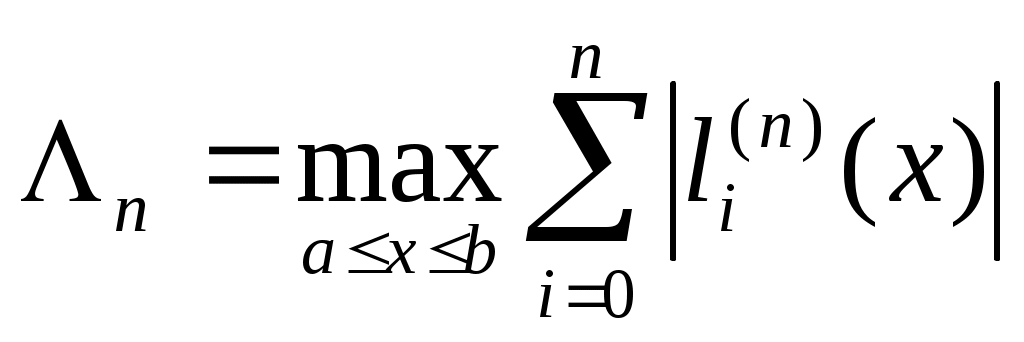 - константа Лебега. - константа Лебега.
Замечание 3. При любом выборе узлов интерполяции 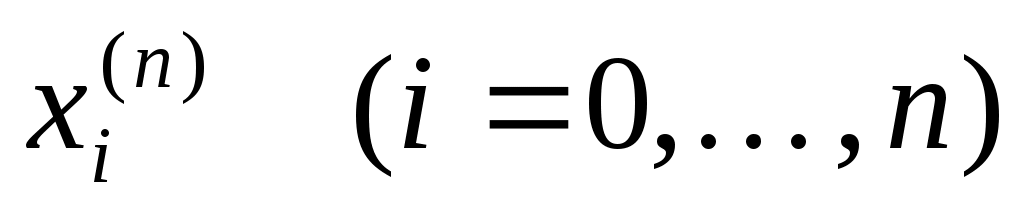 имеет место (см. [4], стр. 118) неравенство С.Н.Бернштейна имеет место (см. [4], стр. 118) неравенство С.Н.Бернштейна 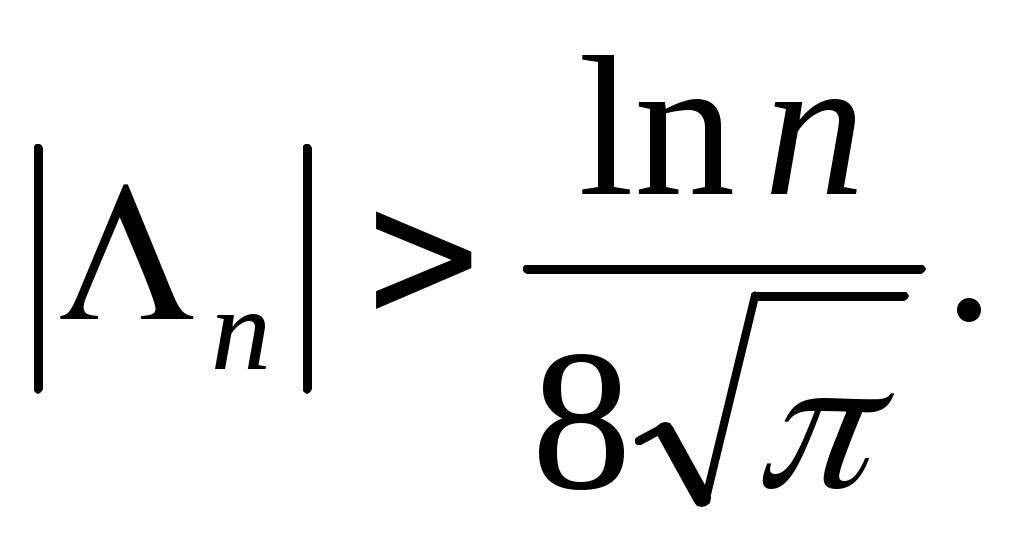 Введем оператор Введем оператор 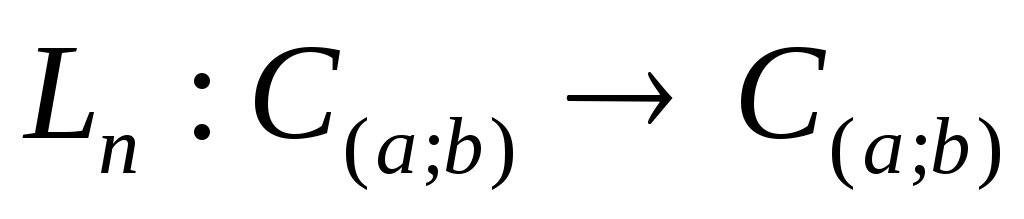 , преобразующий функцию , преобразующий функцию 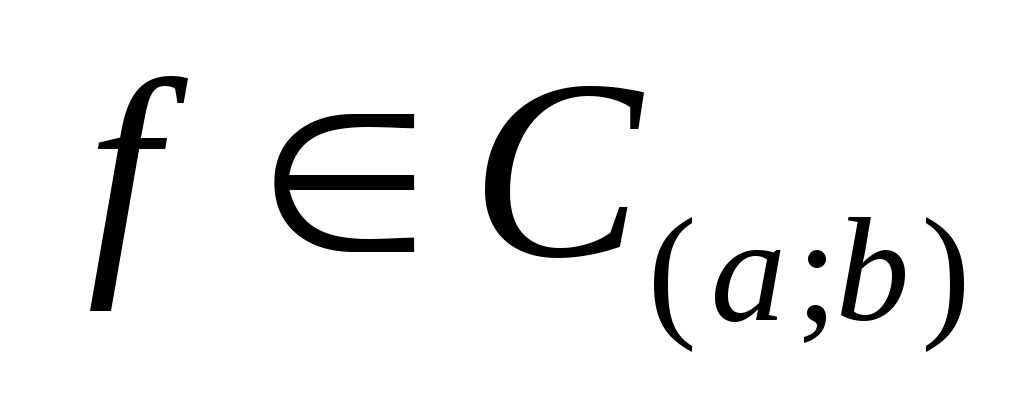 в интерполяционный многочлен Лагранжа в интерполяционный многочлен Лагранжа 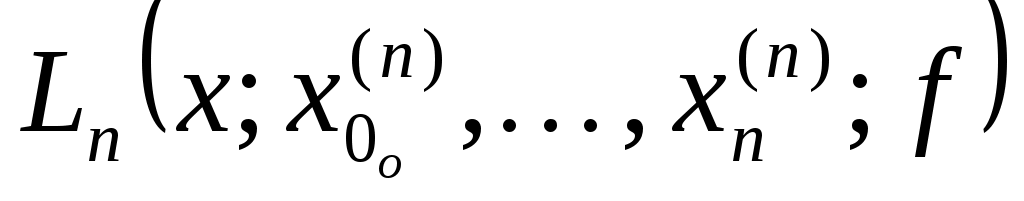 . Оператор . Оператор 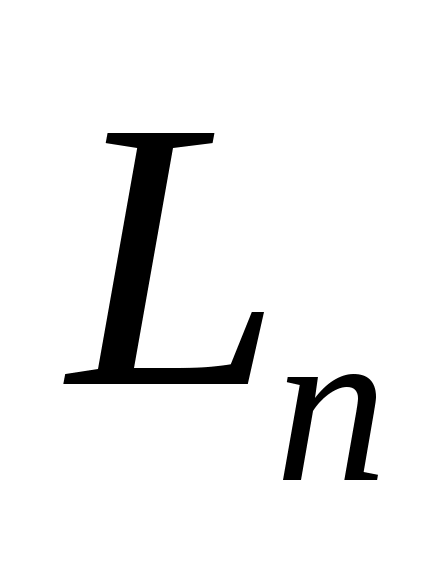 - линейный и ограниченный. Нетрудно показать, что - линейный и ограниченный. Нетрудно показать, что 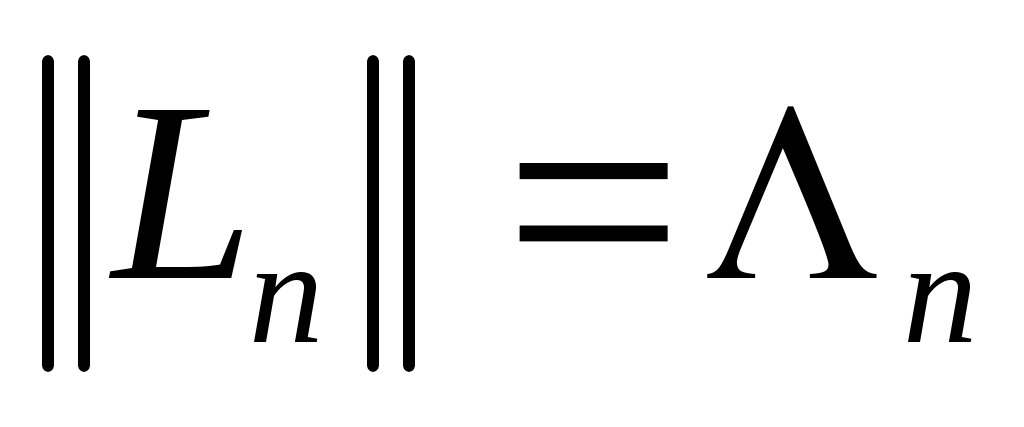 . Из неравенства С.Н.Бернштейна и теоремы Банаха-Штейнгауса немедленно следует, что для любой таблицы узлов интерполяции . Из неравенства С.Н.Бернштейна и теоремы Банаха-Штейнгауса немедленно следует, что для любой таблицы узлов интерполяции  : :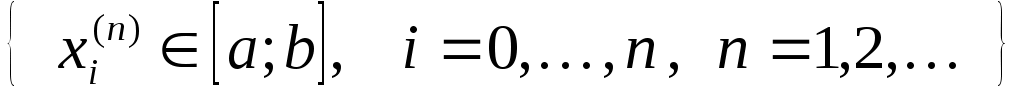 найдется такая функция найдется такая функция 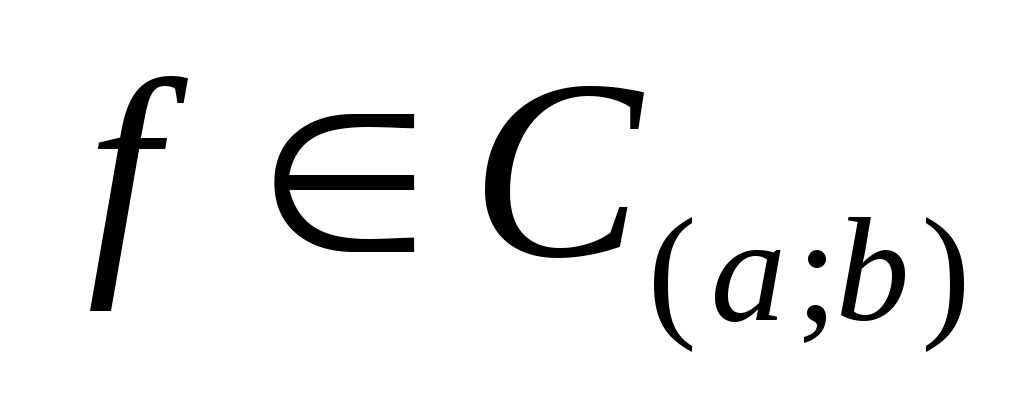 , для которой последовательность интерполяционных многочленов , для которой последовательность интерполяционных многочленов 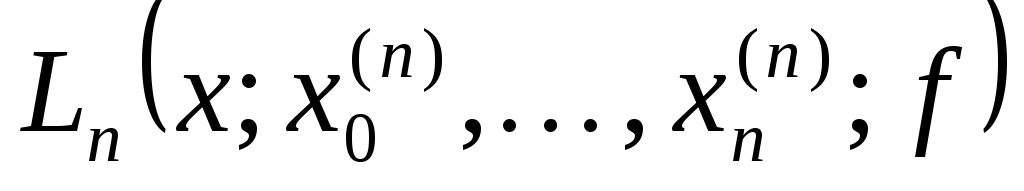 неограниченно расходится. неограниченно расходится.
Замечание 4. Расходимость интерполяционного процесса может вызвать осложнения в задаче вычисления интеграла. При неудачном выборе узлов квадратурный процесс (5), порожденный квадратурной формулой (7)–(8), будет расходящимся (сумма 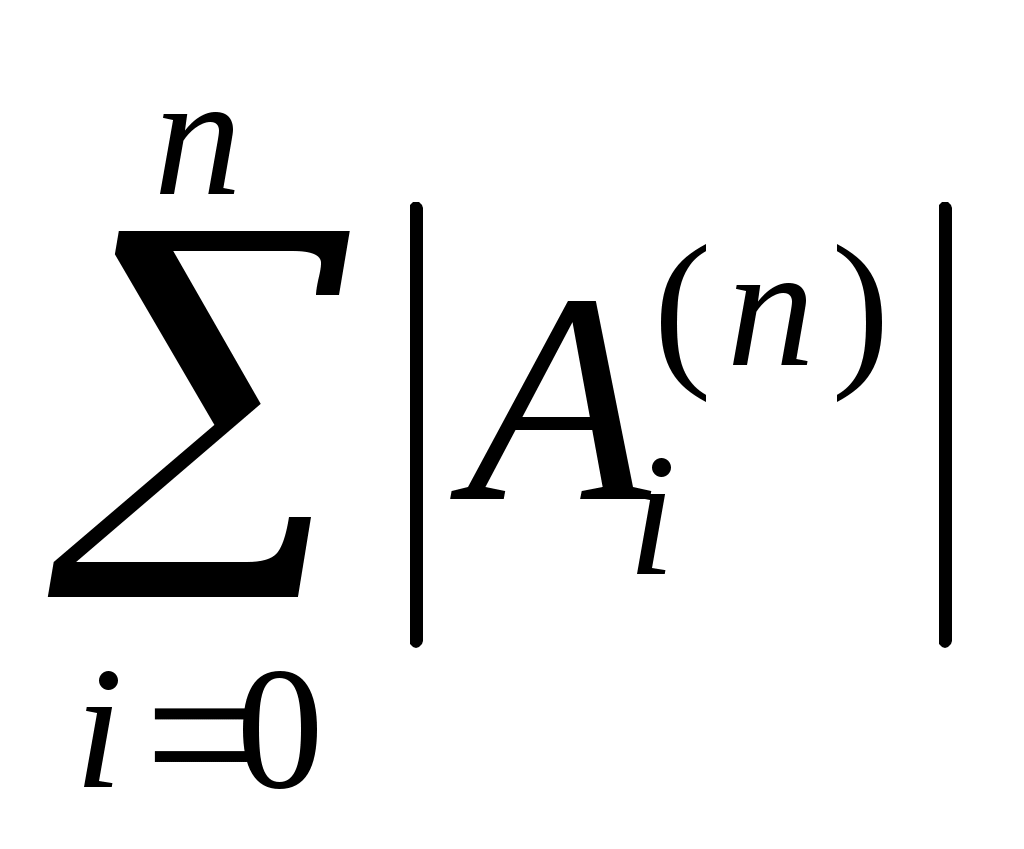 может неограниченно расти). может неограниченно расти).
1.4. Квадратурные формулы Ньютона-Котеса
Возьмем на отрезке 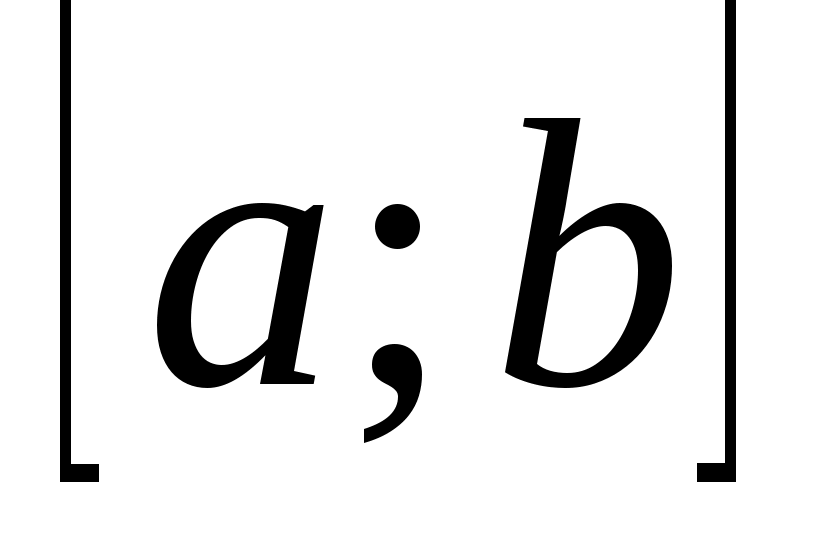 равноотстоящие узлы равноотстоящие узлы 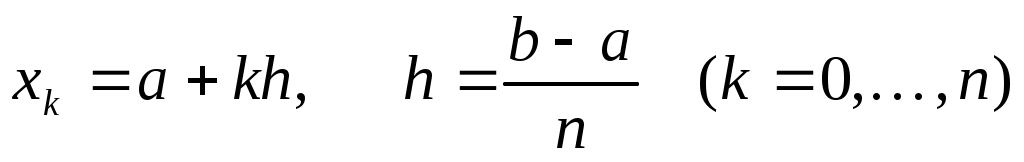  и построим интерполяционную квадратурную формулу (см. (7)-(8)) и построим интерполяционную квадратурную формулу (см. (7)-(8))
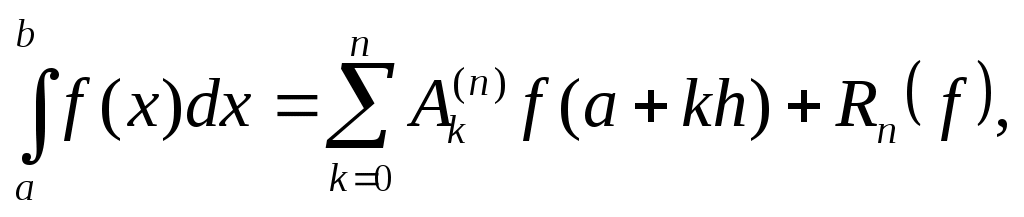
где
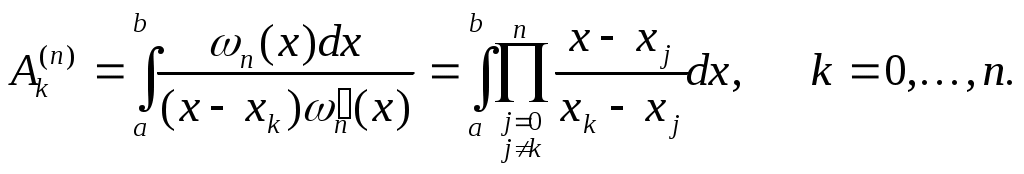
Сделав в интеграле замену переменного 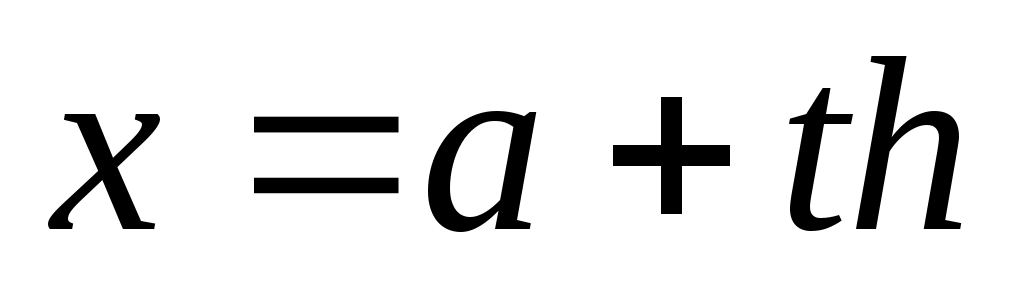 , получим , получим
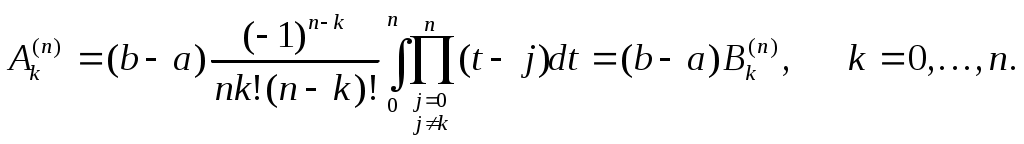
Здесь коэффициенты
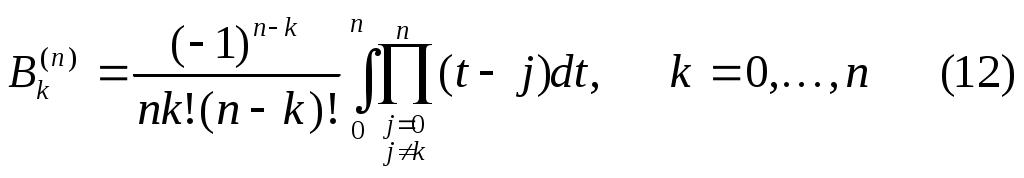
не зависят от промежутка интегрирования и могут быть вычислены заранее.
Интерполяционная квадратурная формула с равноотстоящими узлами и коэффициентами 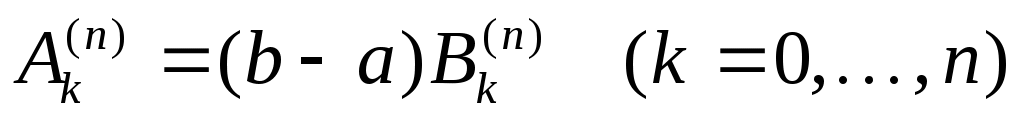 , вычисленными по формуле (12), , вычисленными по формуле (12),
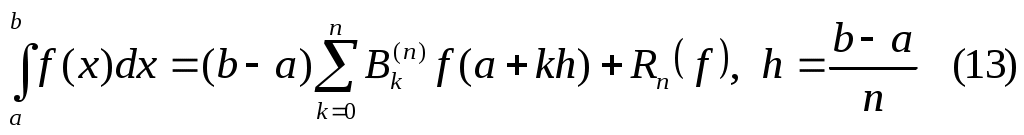
называется квадратурной формулой Ньютона-Котеса.
Коэффициенты 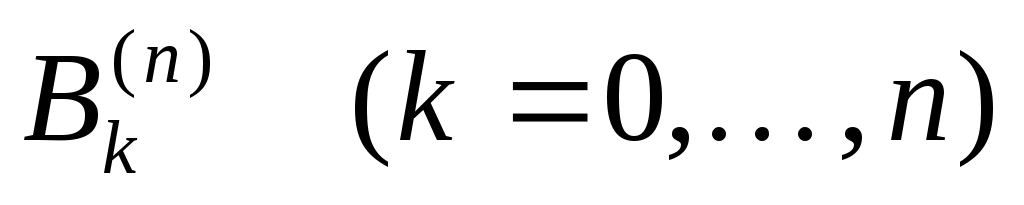 для для  вычислены и содержатся в справочниках по численному интегрированию (см. [3], стр. 16-19). Приведем значения вычислены и содержатся в справочниках по численному интегрированию (см. [3], стр. 16-19). Приведем значения 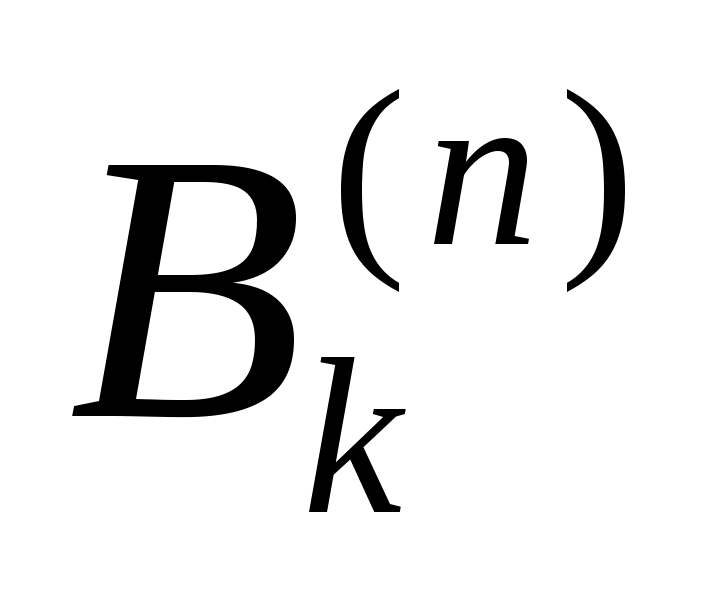 для малых для малых 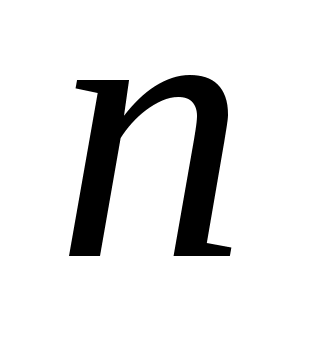 : :
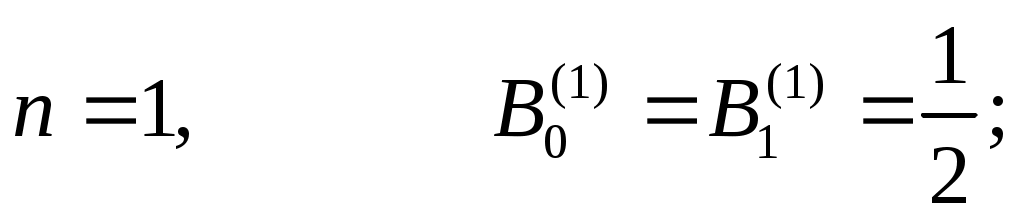
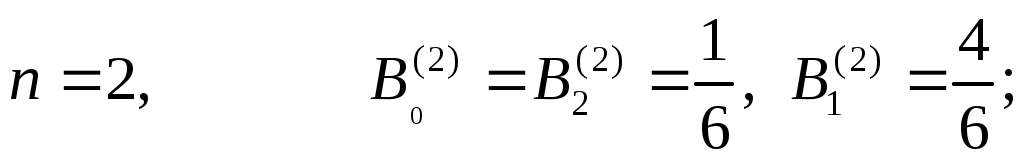
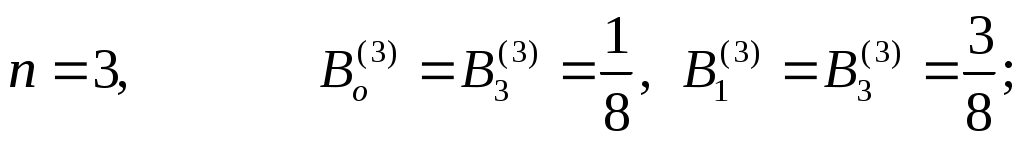
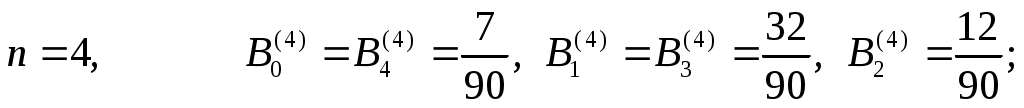
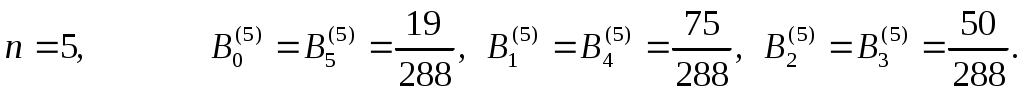
Квадратурная формула Ньютона-Котеса точна на константах: 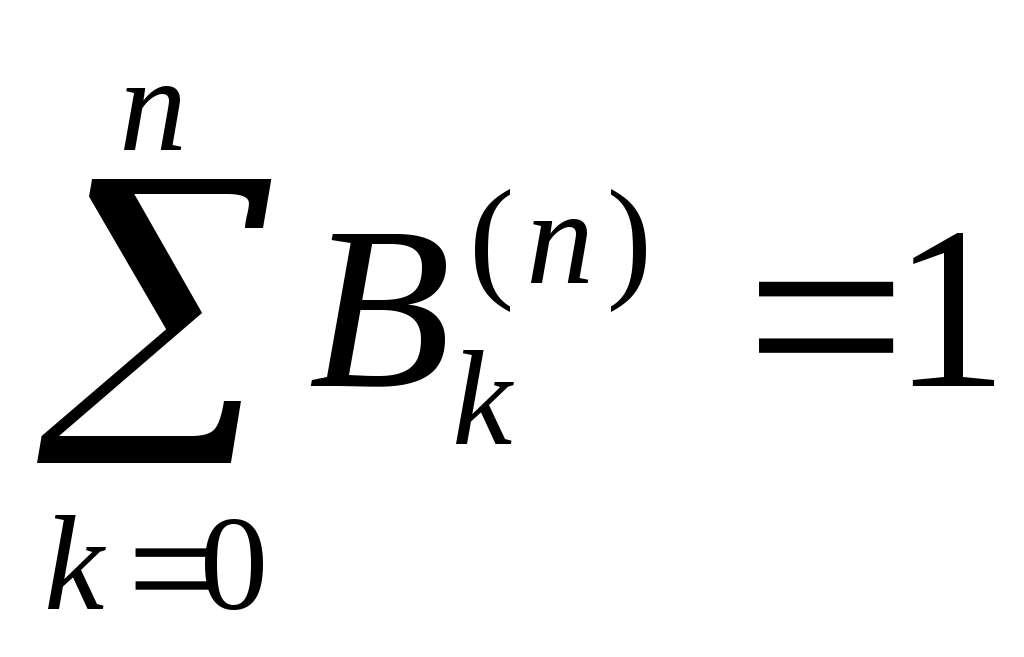 . Для . Для 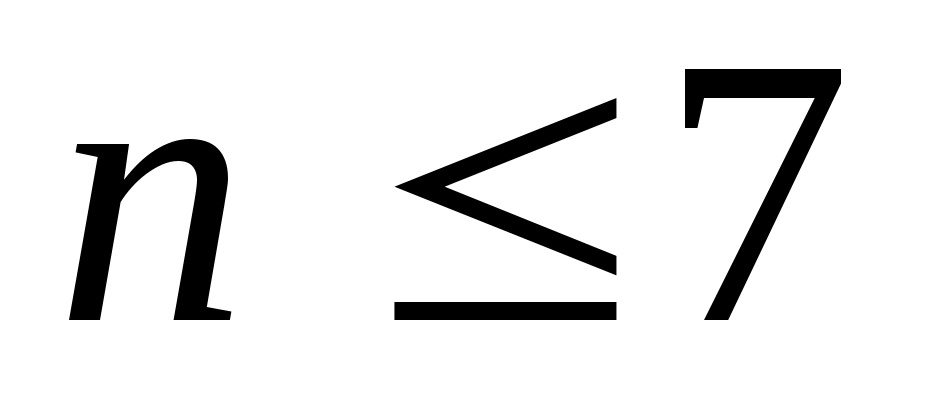 все коэффициенты все коэффициенты 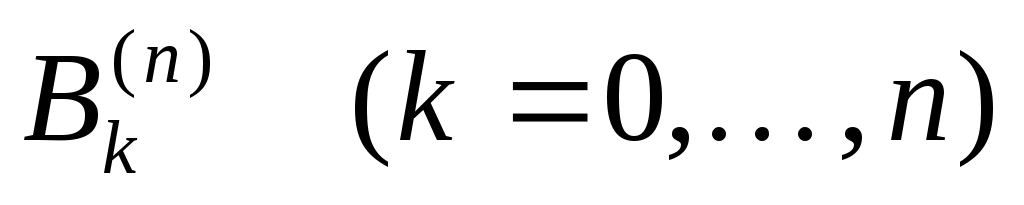 положительны. При положительны. При 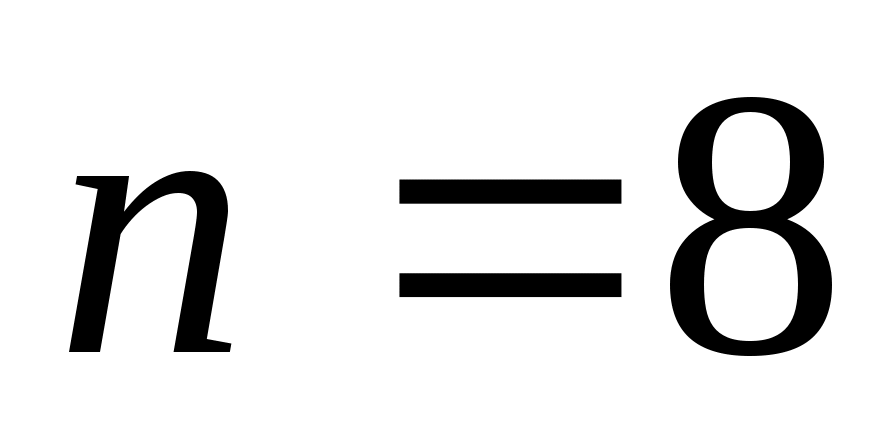 встречаются три отрицательных коэффициента, а при встречаются три отрицательных коэффициента, а при 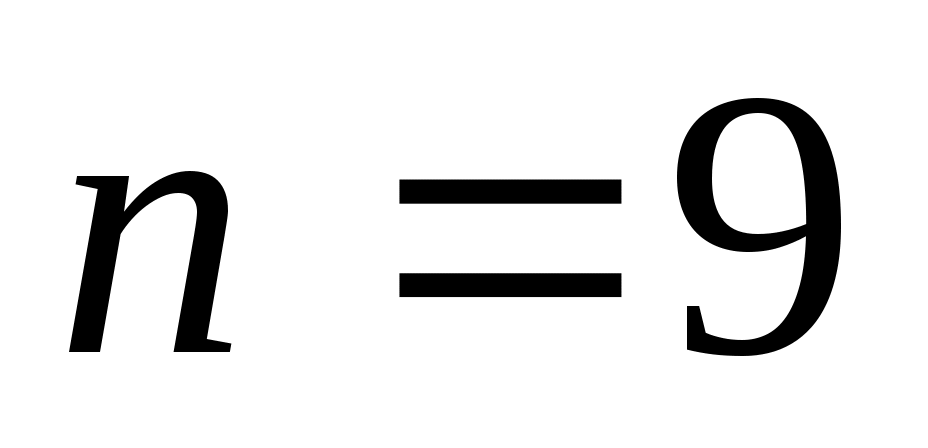 все коэффициенты положительны. Для все коэффициенты положительны. Для 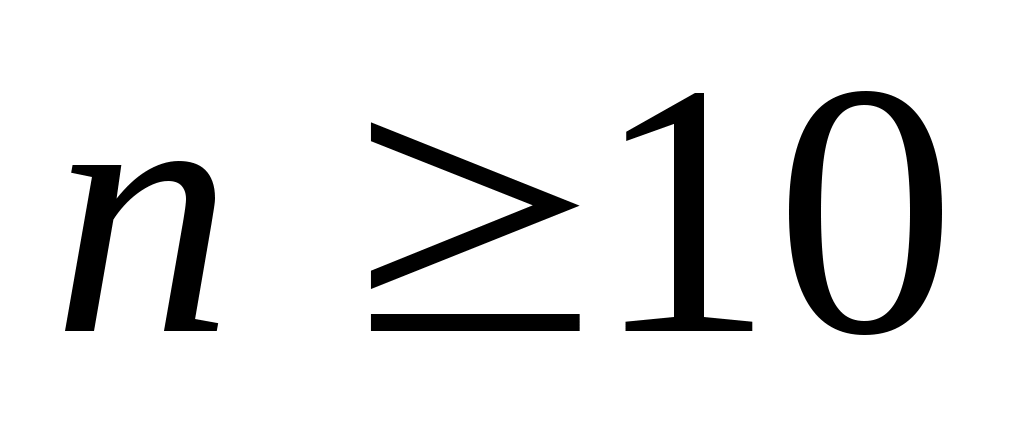 среди среди 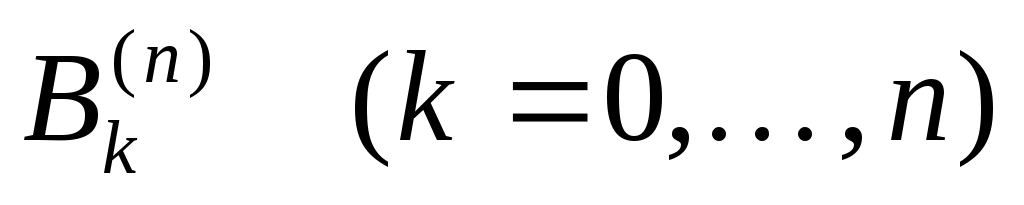 будут отрицательные. Причем имеет место, как показал Д.Пойа, соотношение будут отрицательные. Причем имеет место, как показал Д.Пойа, соотношение
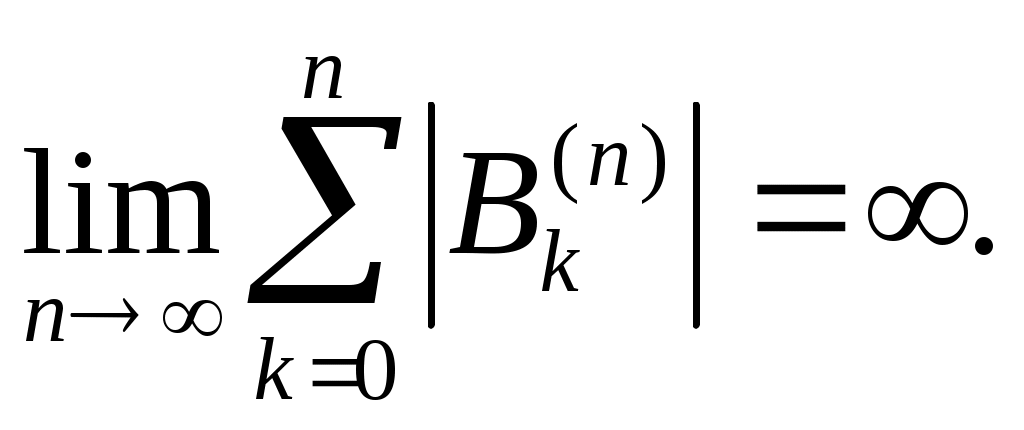
Более того, абсолютные величины 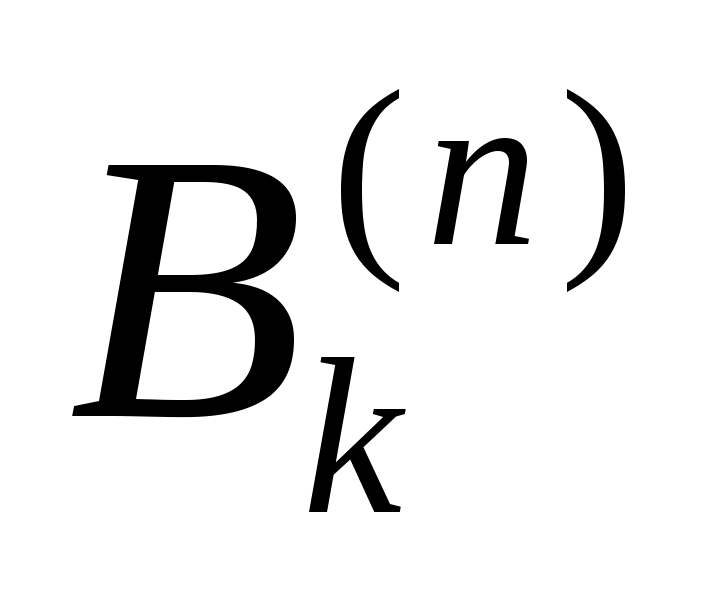 будут довольно быстро расти при будут довольно быстро расти при  для любого фиксированного для любого фиксированного 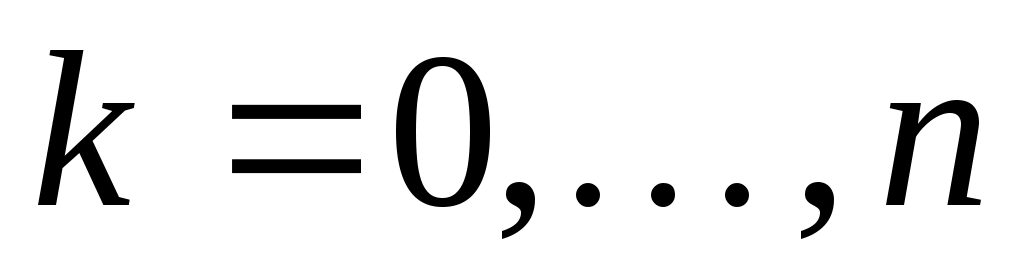 . Это означает, что квадратурный процесс, порожденный квадратурными формулами Ньютона-Котеса (13), является расходящимся (не выполняется условие 2) теоремы 2). Поэтому в приложениях применяются формулы Ньютона-Котеса при небольших значениях . Это означает, что квадратурный процесс, порожденный квадратурными формулами Ньютона-Котеса (13), является расходящимся (не выполняется условие 2) теоремы 2). Поэтому в приложениях применяются формулы Ньютона-Котеса при небольших значениях 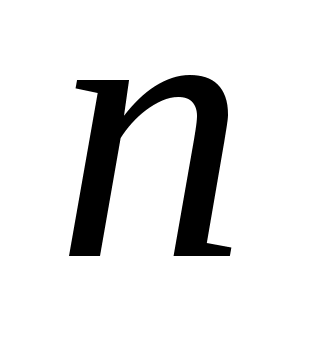 ( (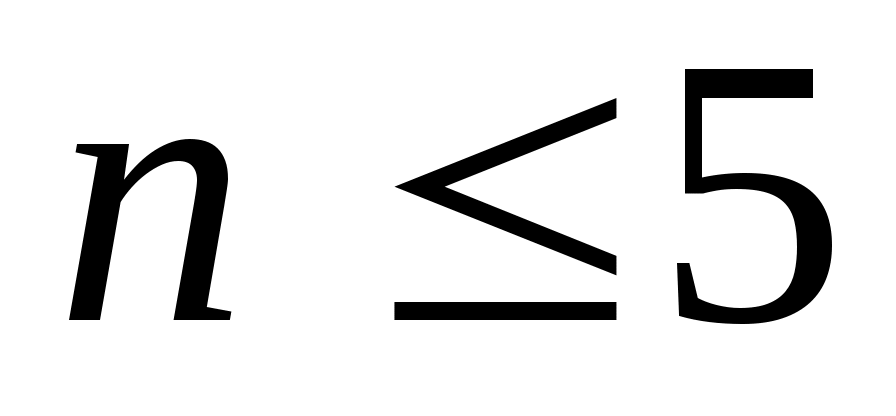 ). ).
Если число узлов 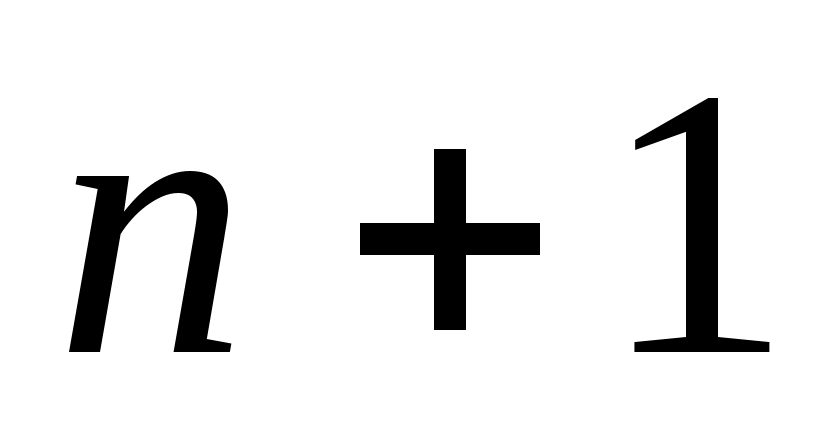 в формуле Ньютона-Котеса (13) нечетное, то алгебраический порядок точности формулы равен в формуле Ньютона-Котеса (13) нечетное, то алгебраический порядок точности формулы равен 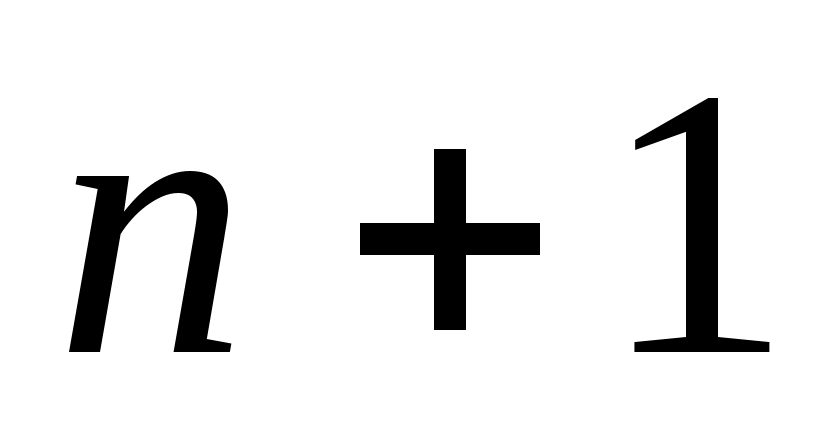 и для и для 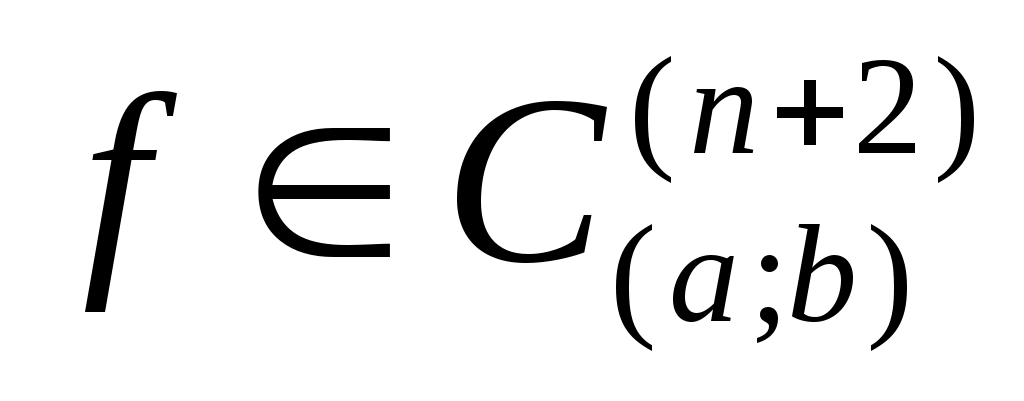 погрешность представима в виде погрешность представима в виде
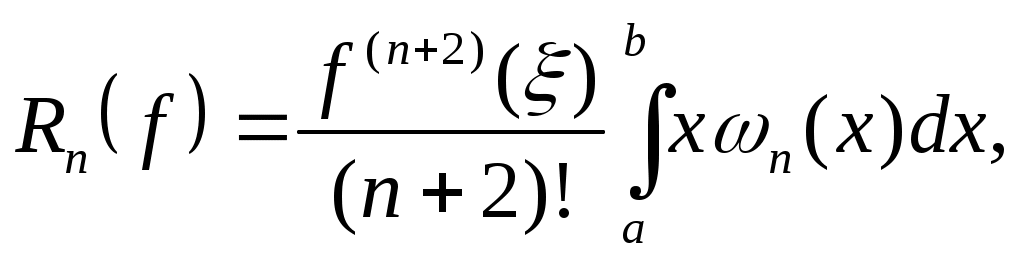
где 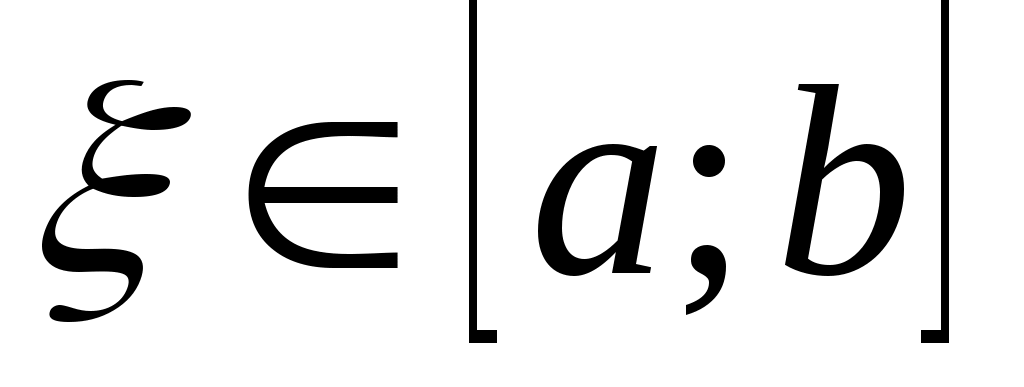 , , 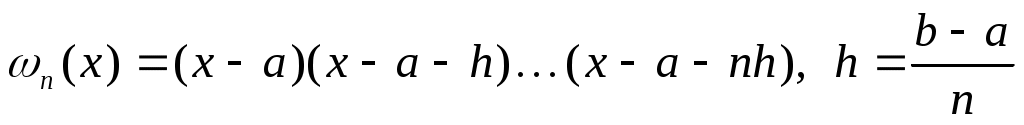 и множитель и множитель 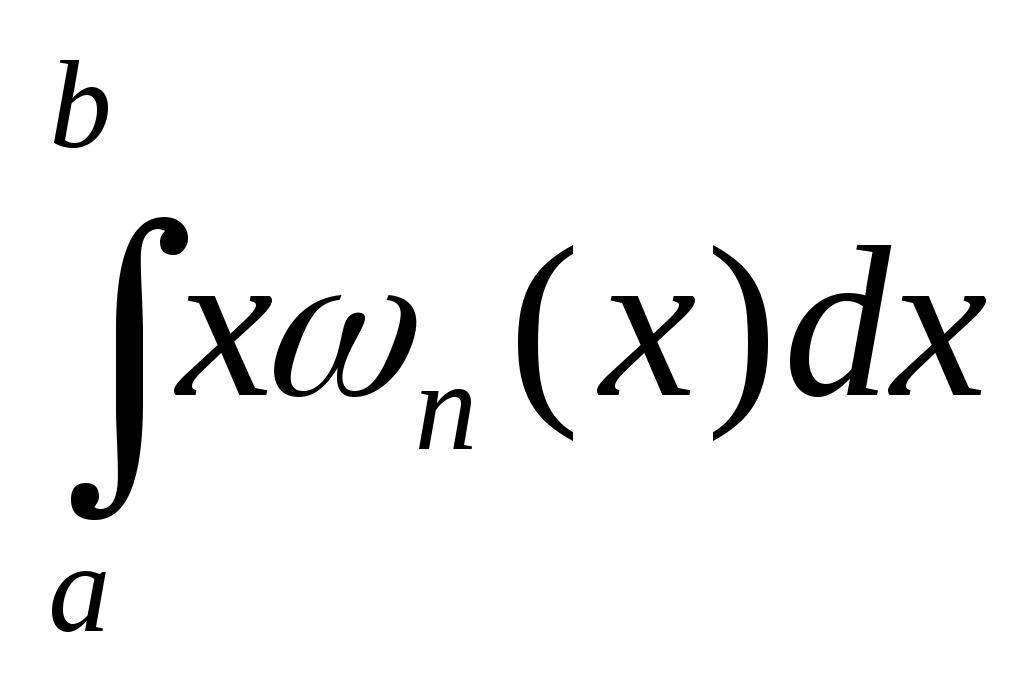 отрицателен. отрицателен.
Если же число узлов 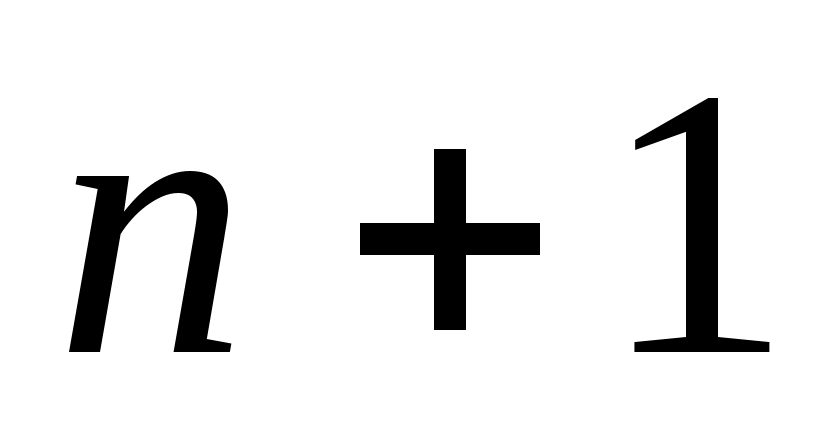 в формуле Ньютона-Котеса (13) четное, то алгебраический порядок точности формулы равен в формуле Ньютона-Котеса (13) четное, то алгебраический порядок точности формулы равен 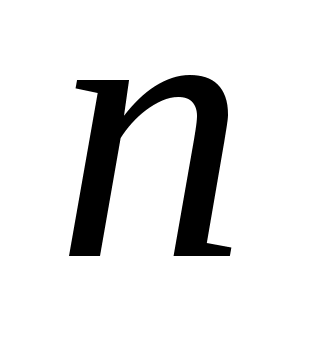 и для и для  погрешность представима в виде погрешность представима в виде
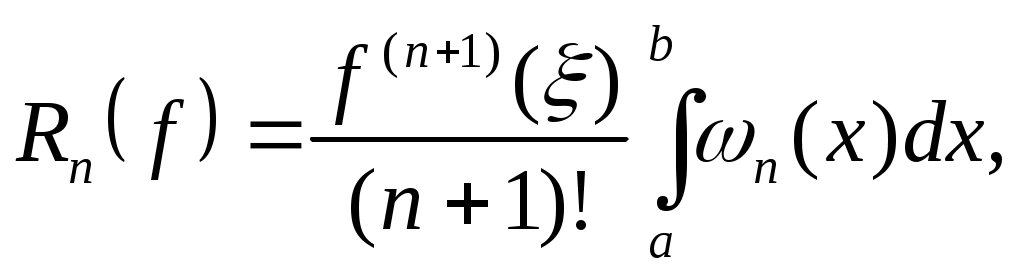
здесь 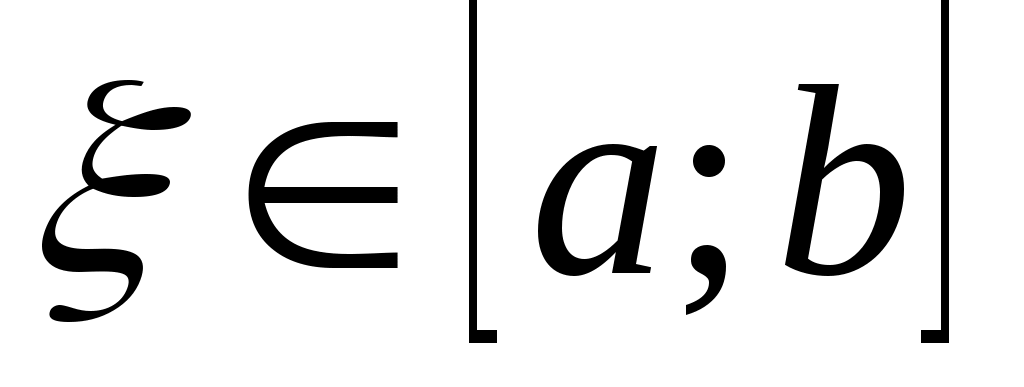 , , 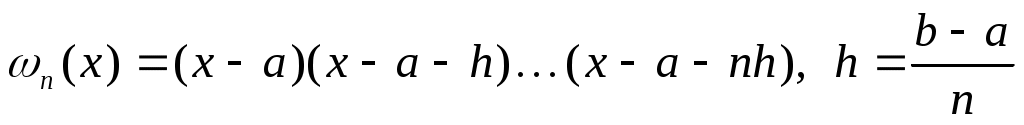 и множитель и множитель 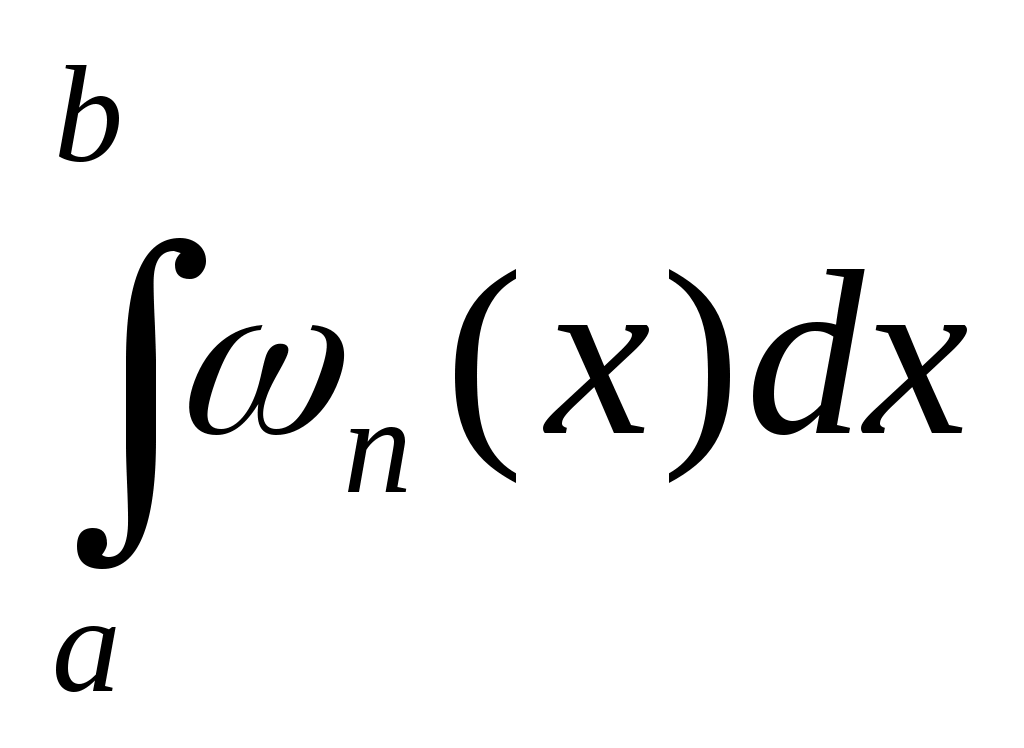 отрицателен. отрицателен.
Приведем наиболее распространенные формулы Ньютона-Котеса:
Формула трапеций
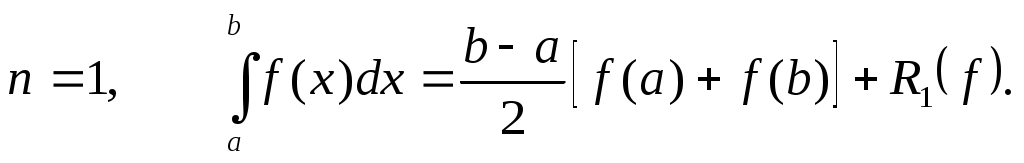
Если 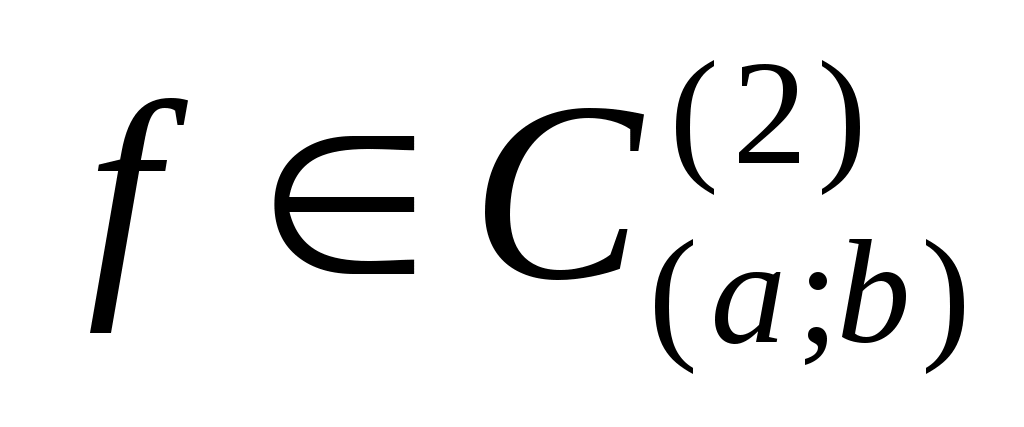 , то , то 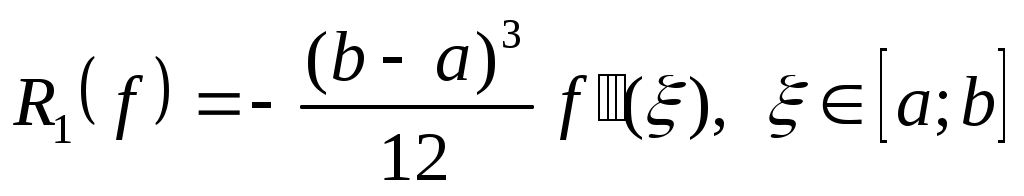 . .
Формула Симпсона (парабол)
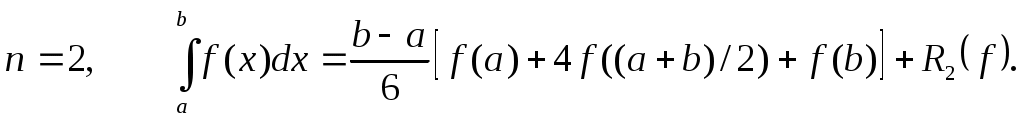
Если 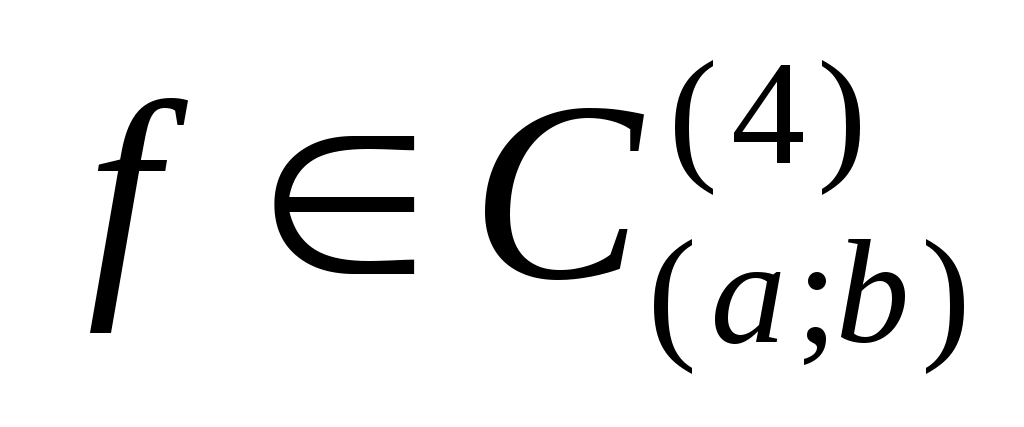 , то , то 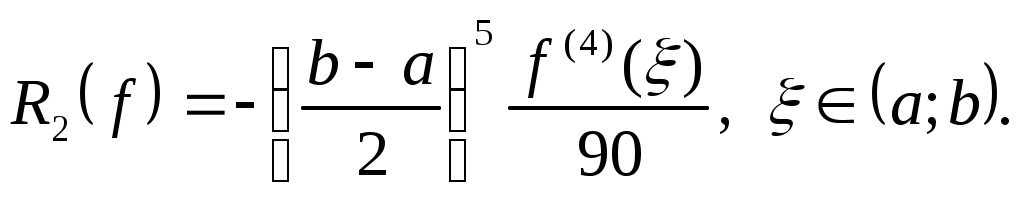
Формула трех восьмых
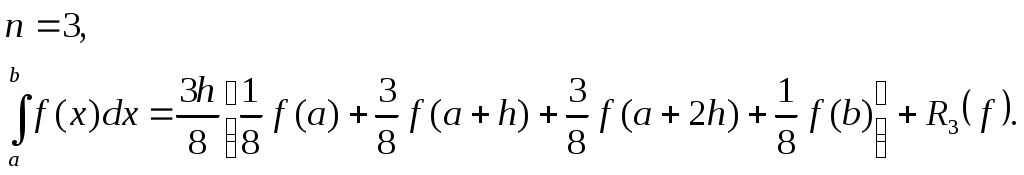
Если 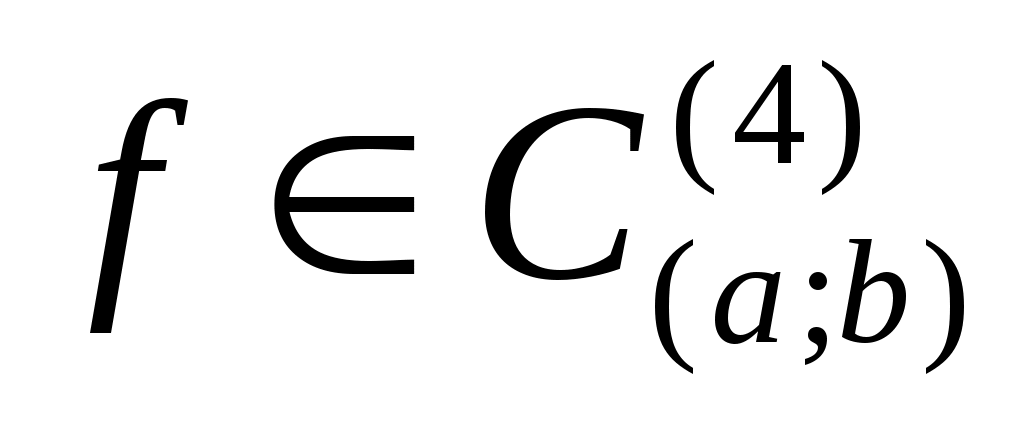 , то , то 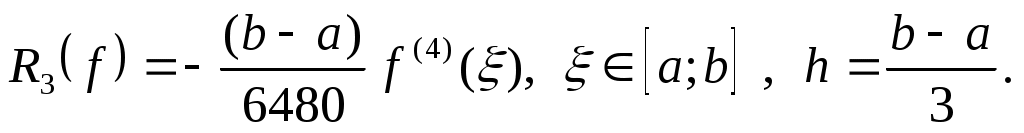
1.5. Квадратурные формулы Гаусса
Пусть требуется построить квадратурную формулу с 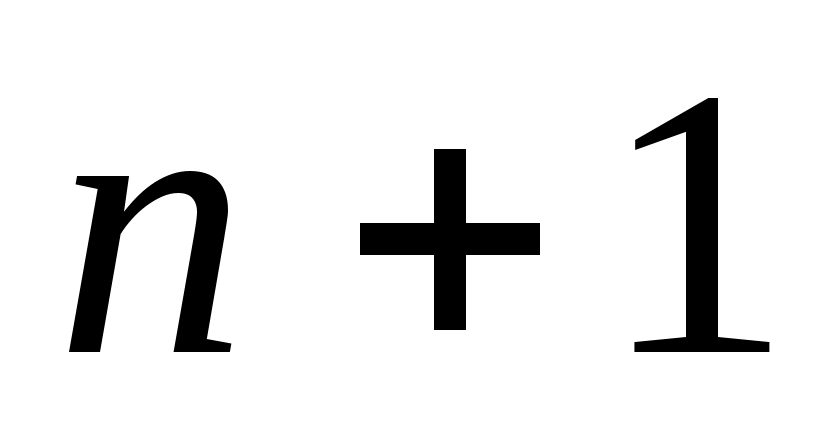 узлами, имеющую максимально возможный алгебраический порядок точности. Нужно определить узлами, имеющую максимально возможный алгебраический порядок точности. Нужно определить 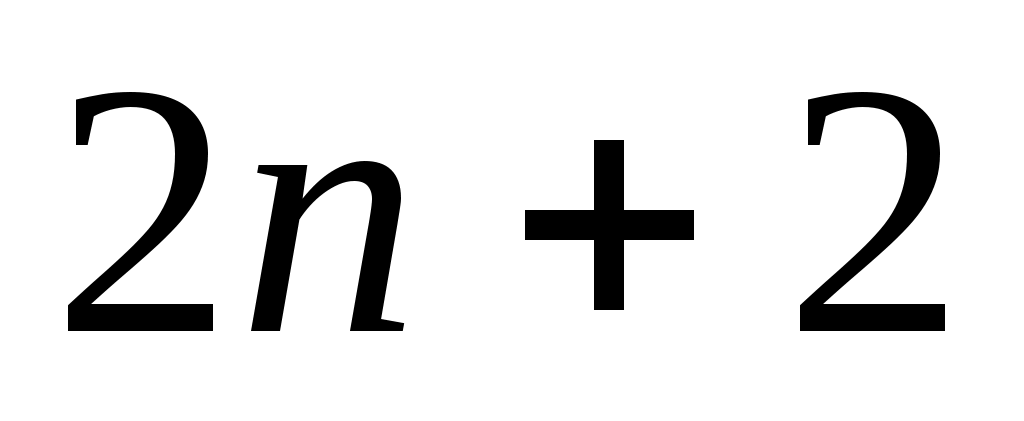 параметра квадратурной формулы: узлы параметра квадратурной формулы: узлы 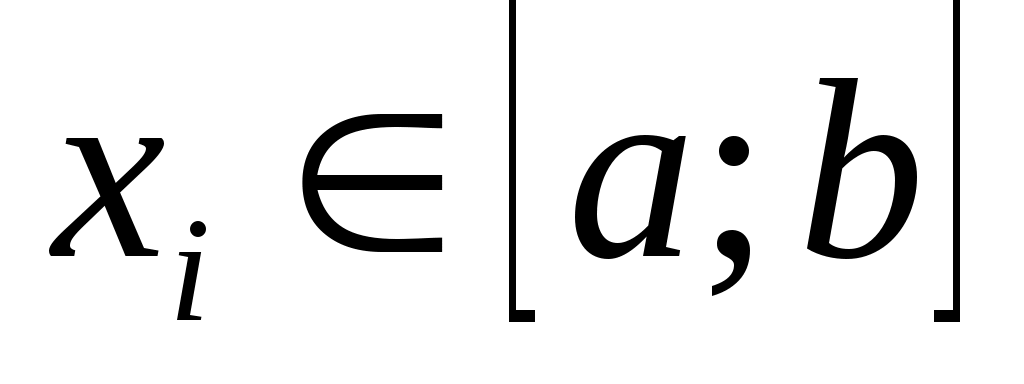 и коэффициенты и коэффициенты 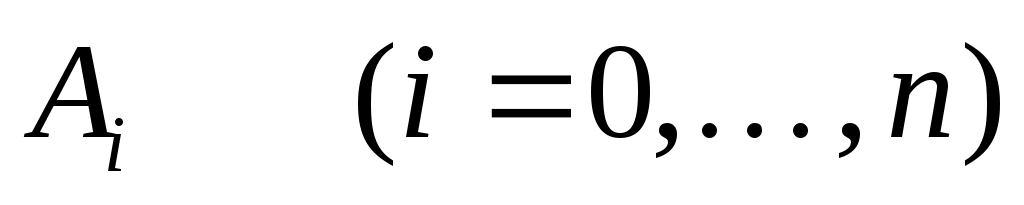 . .
Ясно, что наивысший алгебраический порядок точности квадратурной формулы с 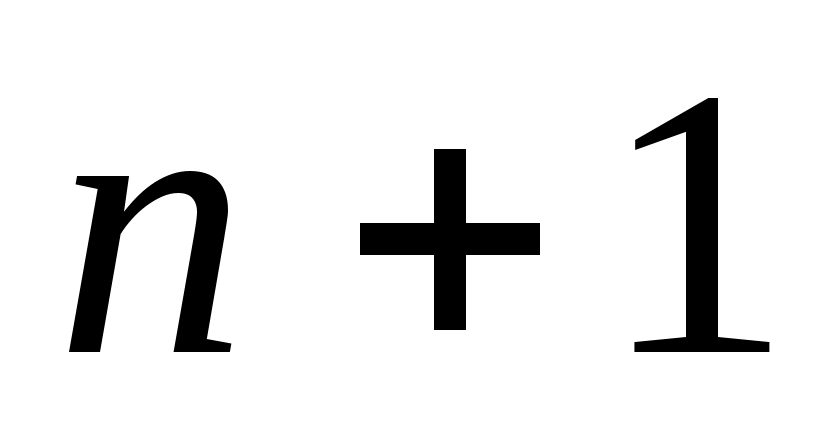 узлами не может быть выше, чем узлами не может быть выше, чем 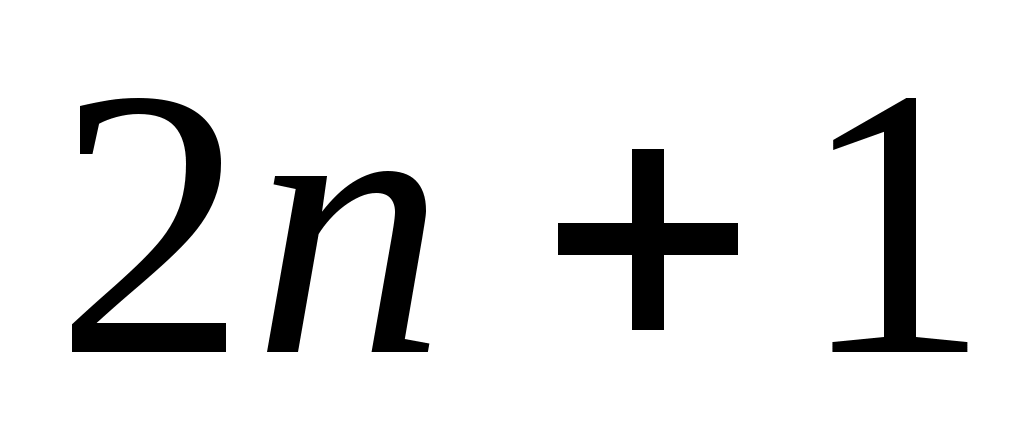 . Действительно, возьмем многочлен . Действительно, возьмем многочлен 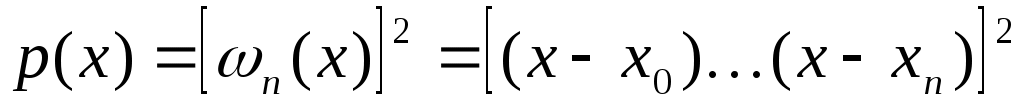 степени степени 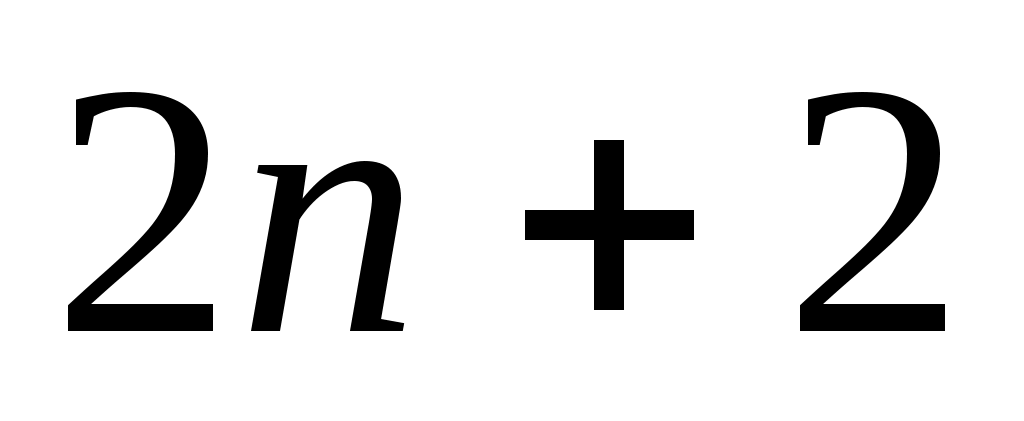 . Тогда . Тогда 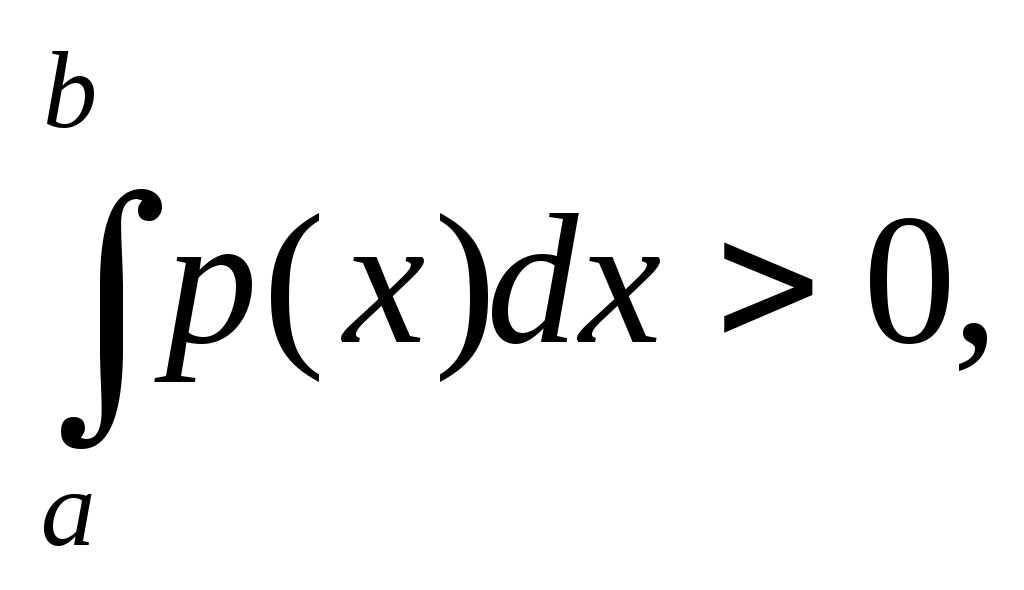 но но 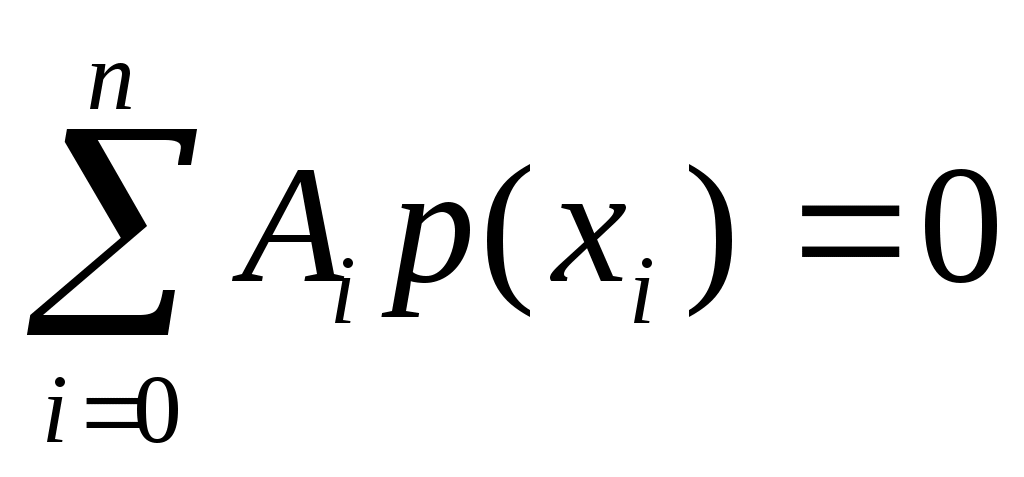 и, следовательно, погрешность квадратурной формулы и, следовательно, погрешность квадратурной формулы 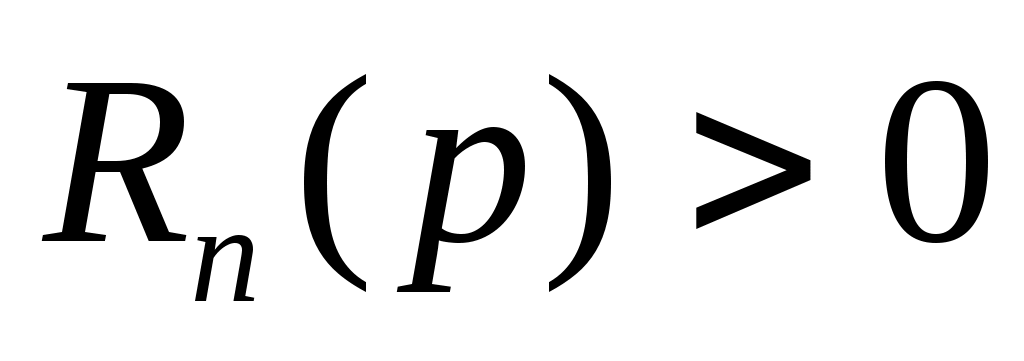 . .
Теперь мы можем попытаться построить квадратурную формулу с алгебраическим порядком точности 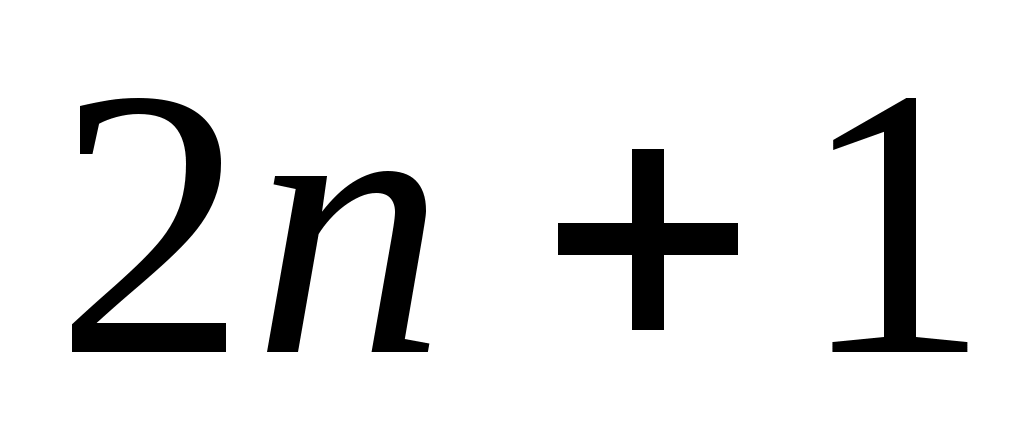 . .
Теорема 3. Для того чтобы квадратурная формула (2) с 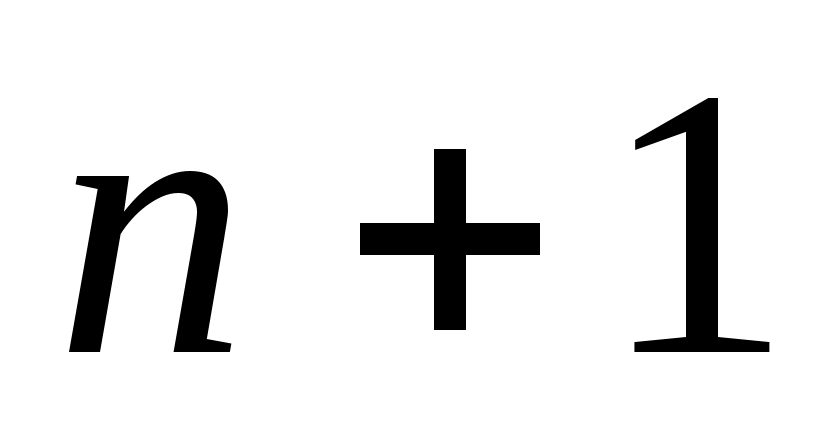 узлами узлами 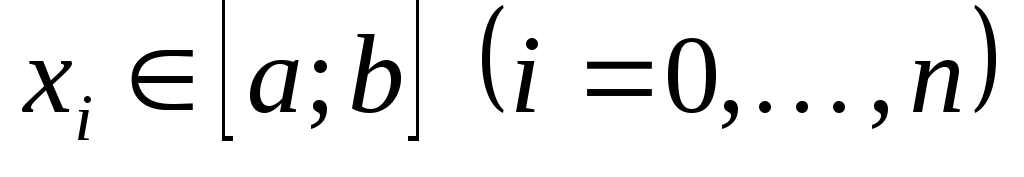 имела алгебраический порядок точности имела алгебраический порядок точности 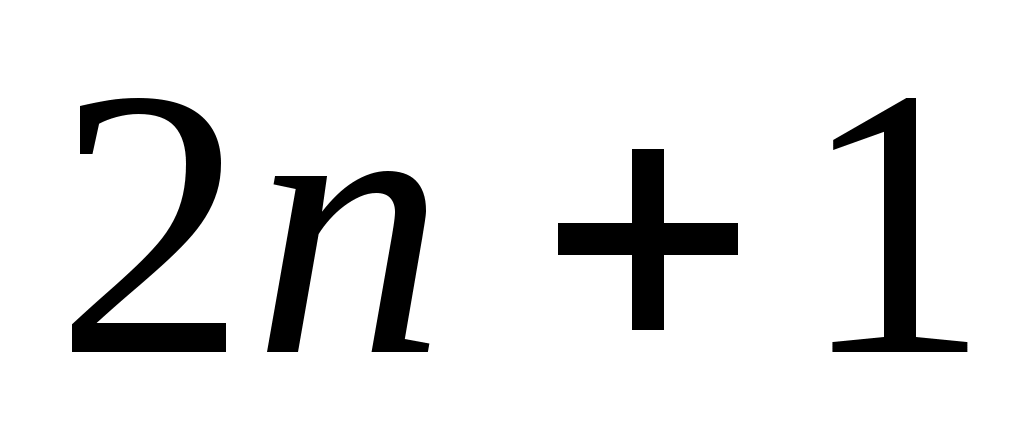 , необходимо и достаточно, чтобы многочлен , необходимо и достаточно, чтобы многочлен 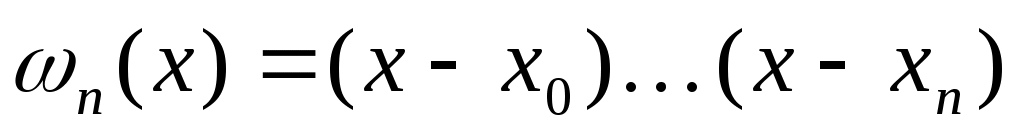 степени степени 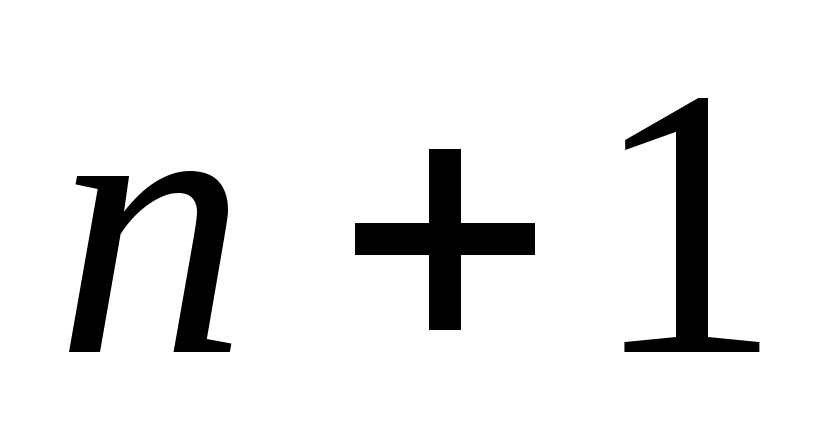 был ортогонален на был ортогонален на 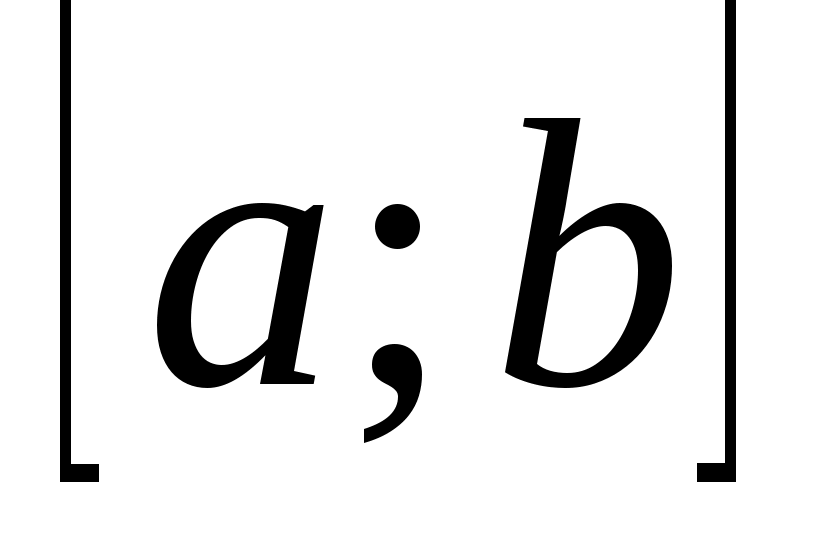 любому многочлену любому многочлену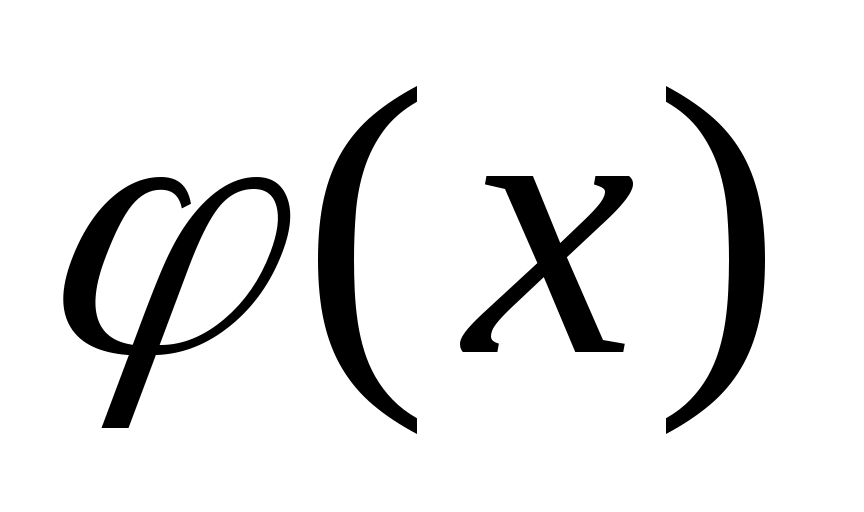 степени меньшей или равной степени меньшей или равной 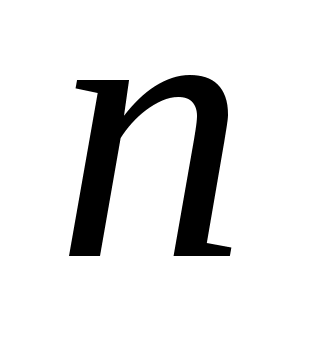 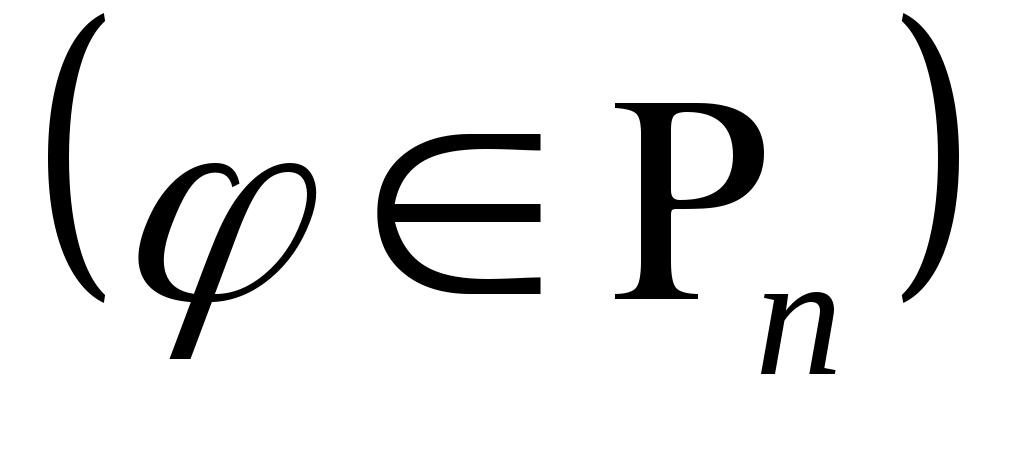 , то есть для любого многочлена , то есть для любого многочлена 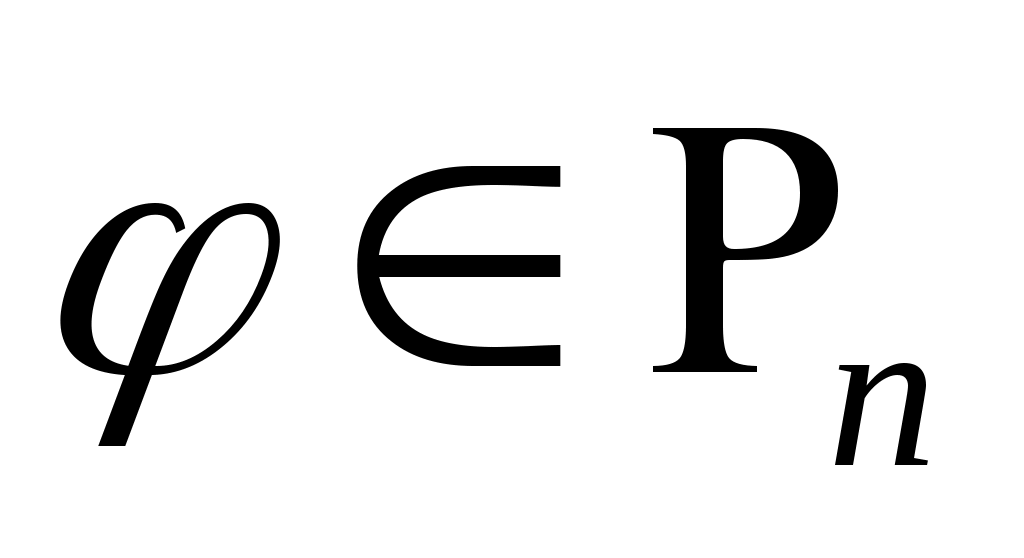
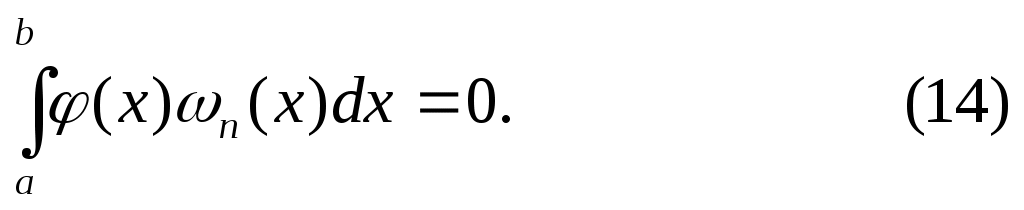
Квадратурная формула с 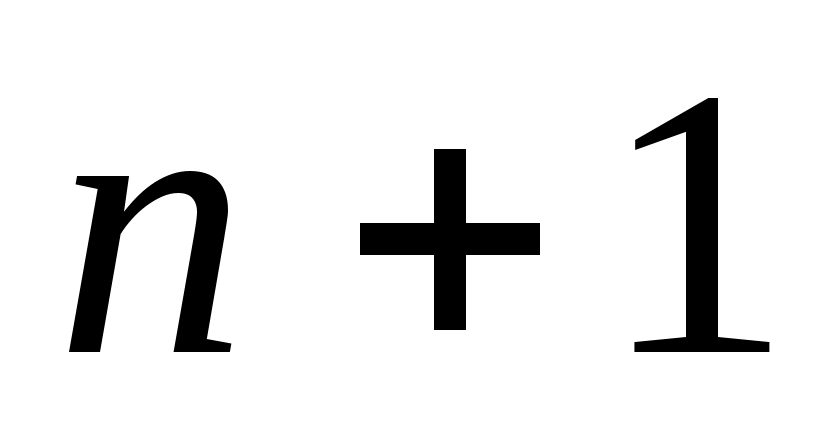 узлами, имеющая алгебраический порядок точности узлами, имеющая алгебраический порядок точности 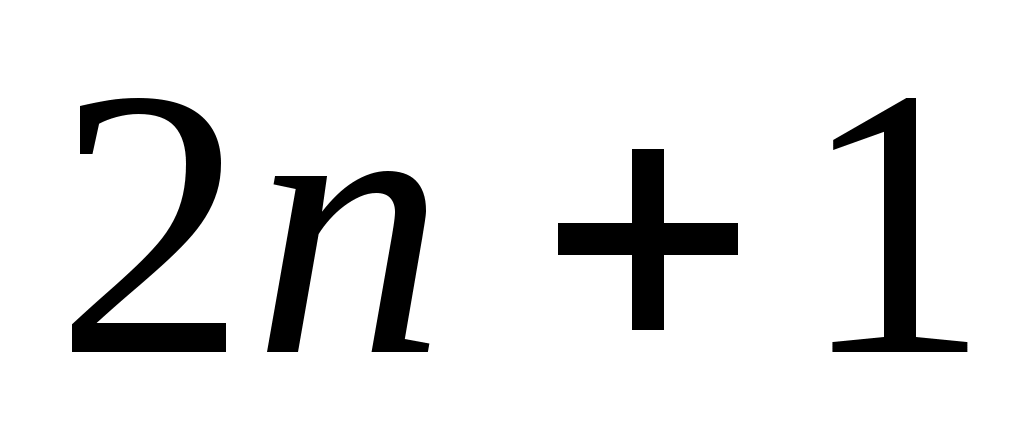 , называется квадратурной формулой Гаусса или квадратурной формулой наивысшего алгебраического порядка точности. Очевидно, что квадратурная формула Гаусса является интерполяционной. , называется квадратурной формулой Гаусса или квадратурной формулой наивысшего алгебраического порядка точности. Очевидно, что квадратурная формула Гаусса является интерполяционной.
Для любого 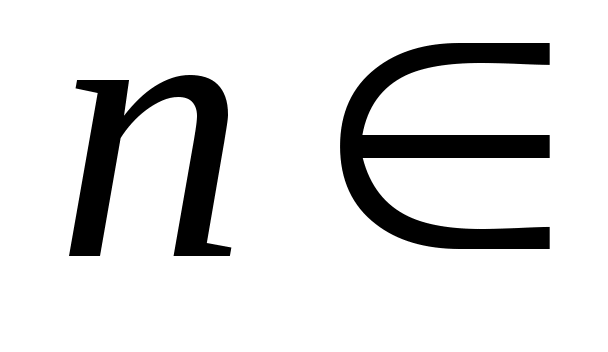 N многочлен степени N многочлен степени 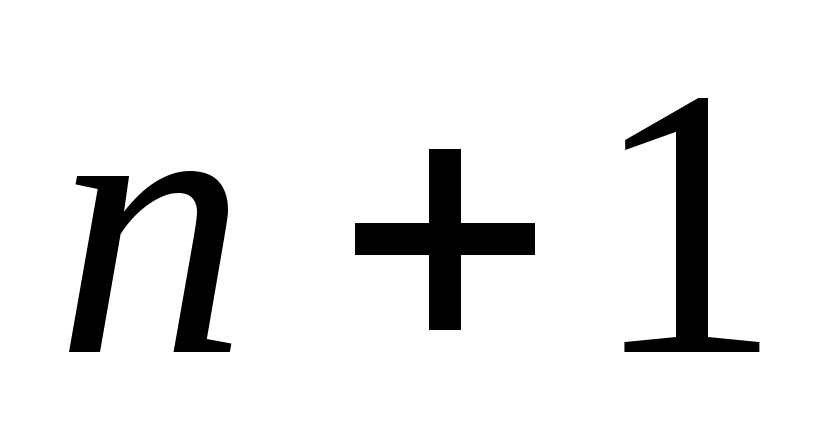 , удовлетворяющий условию ортогональности (14), имеющий вещественные и различные корни , удовлетворяющий условию ортогональности (14), имеющий вещественные и различные корни 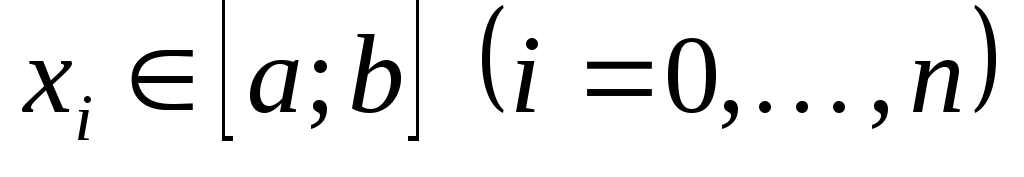 , существует и единственен. Поэтому квадратурная формула Гаусса может быть построена. , существует и единственен. Поэтому квадратурная формула Гаусса может быть построена.
Для коэффициентов 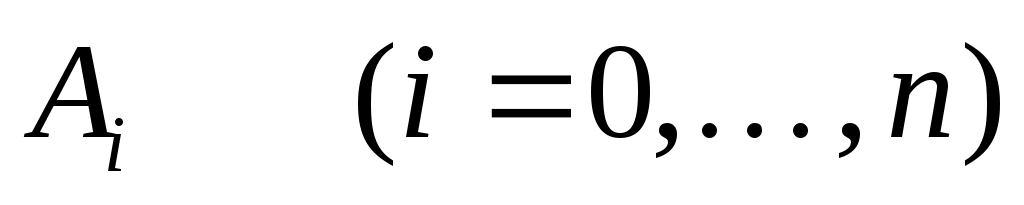 квадратурной формулы Гаусса верно следующее равенство квадратурной формулы Гаусса верно следующее равенство
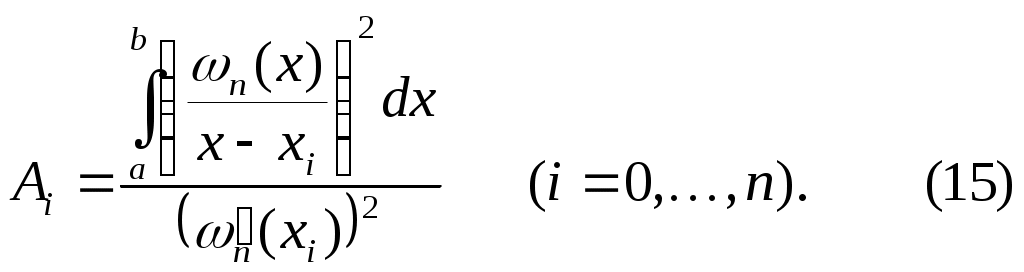
Следовательно, все 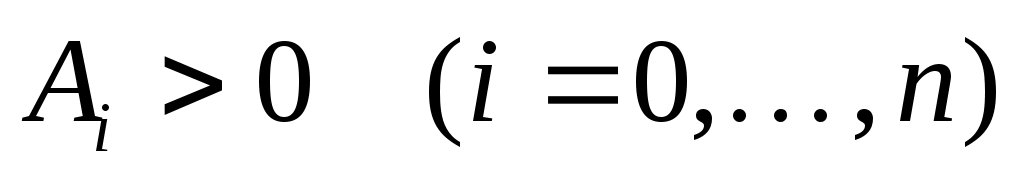 и и 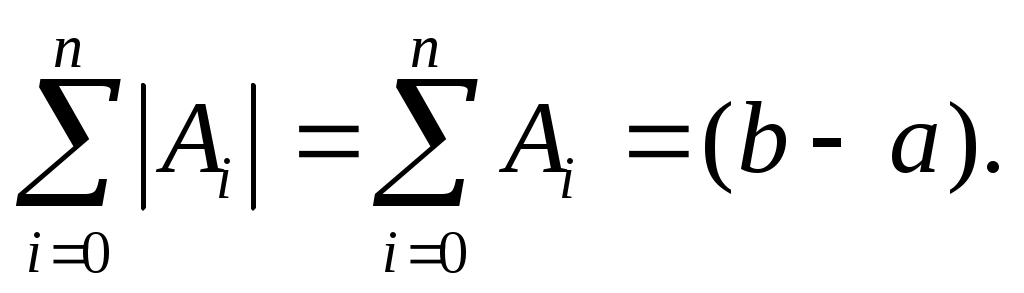 Отсюда и из теоремы 2 вытекает сходимость квадратурного процесса, порожденного квадратурной формулой Гаусса. Отсюда и из теоремы 2 вытекает сходимость квадратурного процесса, порожденного квадратурной формулой Гаусса.
Квадратурная формула Гаусса дает высокую точность в том случае, когда подинтегральная функция  в окрестности отрезка интегрирования обладает высоким порядком гладкости. в окрестности отрезка интегрирования обладает высоким порядком гладкости.
Погрешность квадратурной формулы Гаусса для 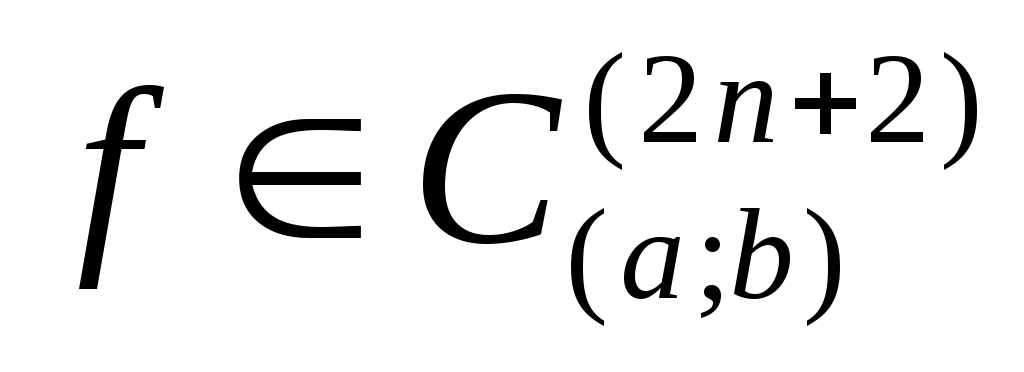 имеет вид имеет вид
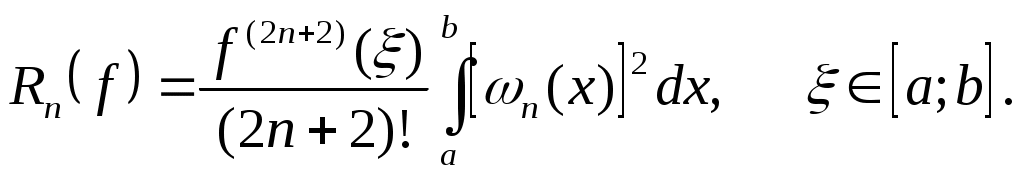
Исторически первым примером квадратурной формулы, имеющей наивысший алгебраический порядок точности, была формула Гаусса для отрезка 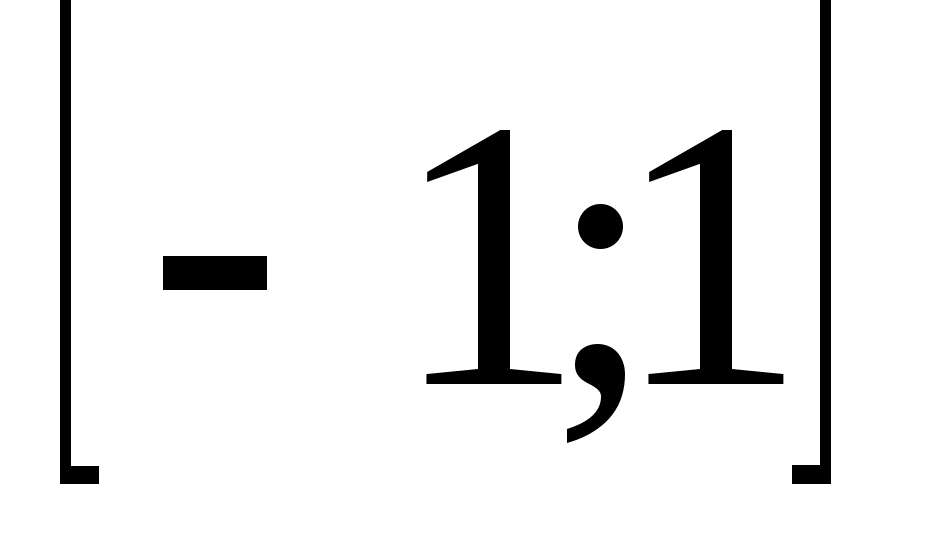 . Для построения квадратурной формулы использовалась система ортогональных многочленов Лежандра. . Для построения квадратурной формулы использовалась система ортогональных многочленов Лежандра.
Многочлены вида
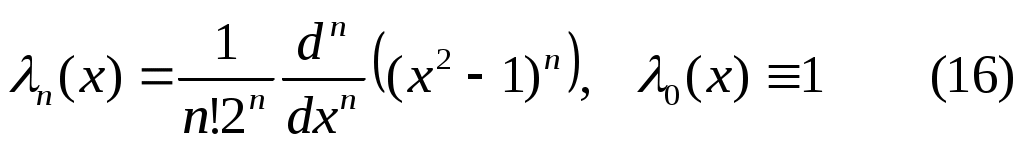
называются многочленами Лежандра. Из (16) следует, что 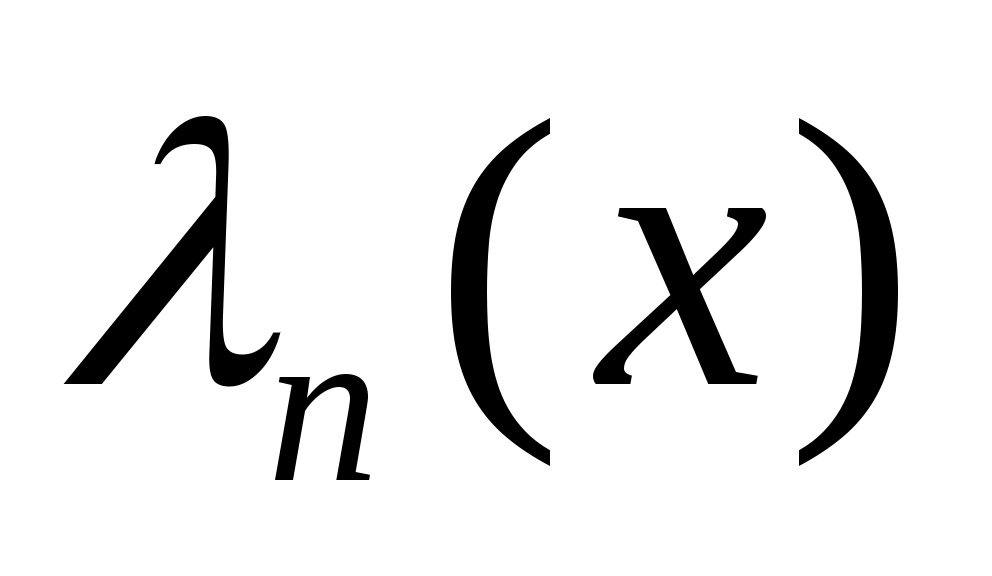 является многочленом степени является многочленом степени 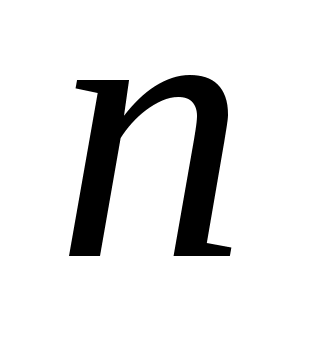 . .
Многочлены Лежандра обладают следующими свойствами:
1. Многочлен 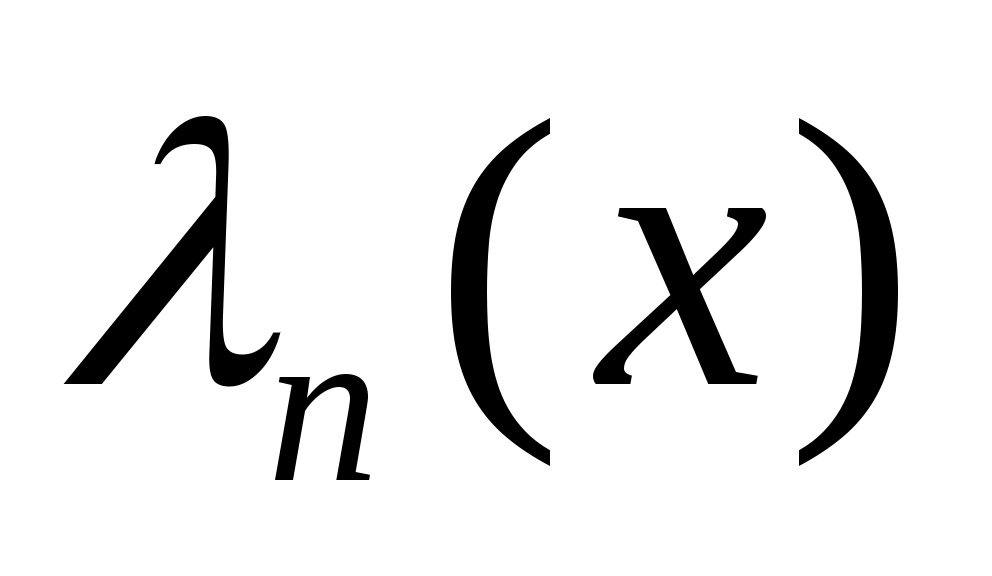 ортогонален на отрезке ортогонален на отрезке 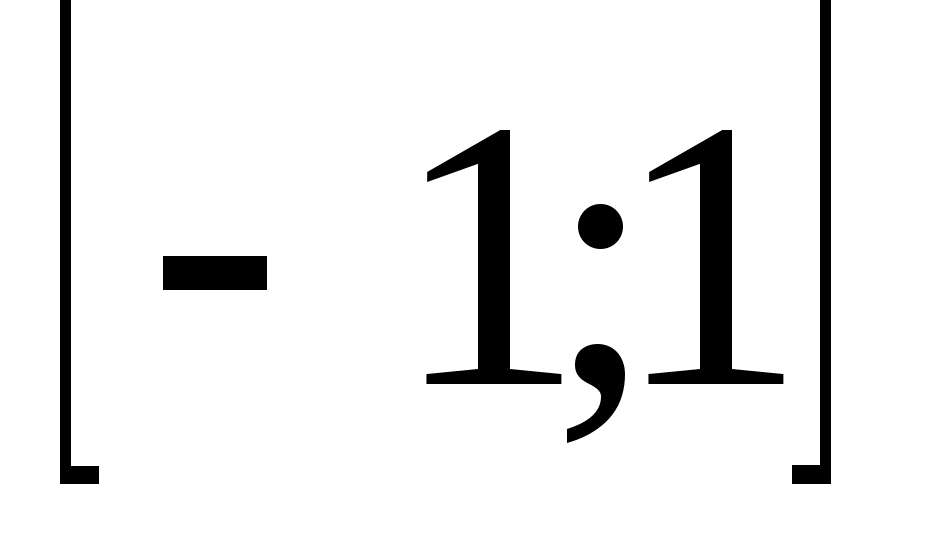 любому многочлену любому многочлену 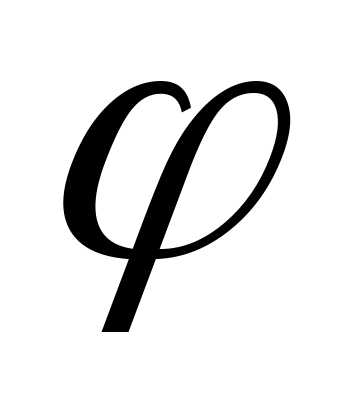 степени меньше степени меньше 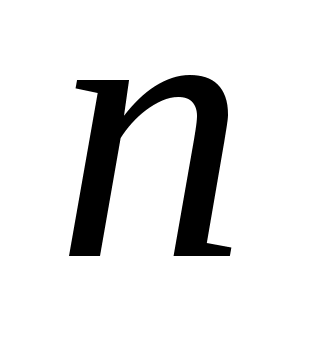 : : 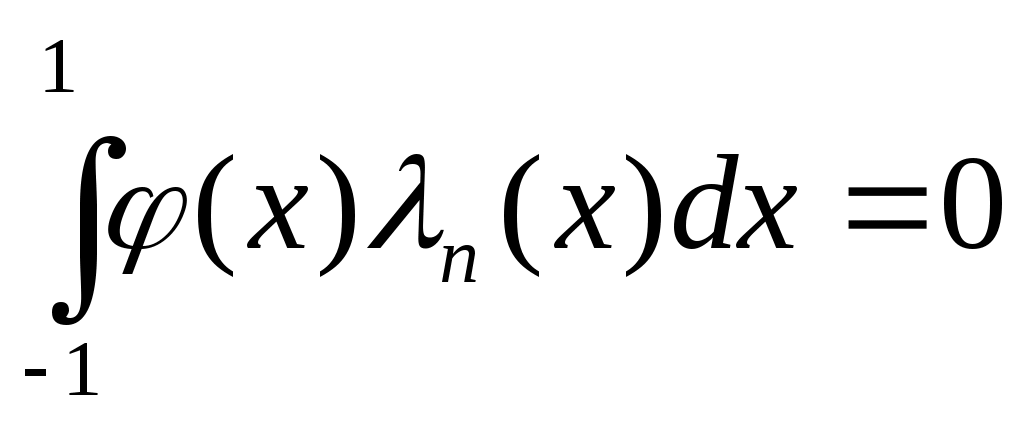 для любого для любого  . .
2. Все корни многочлена 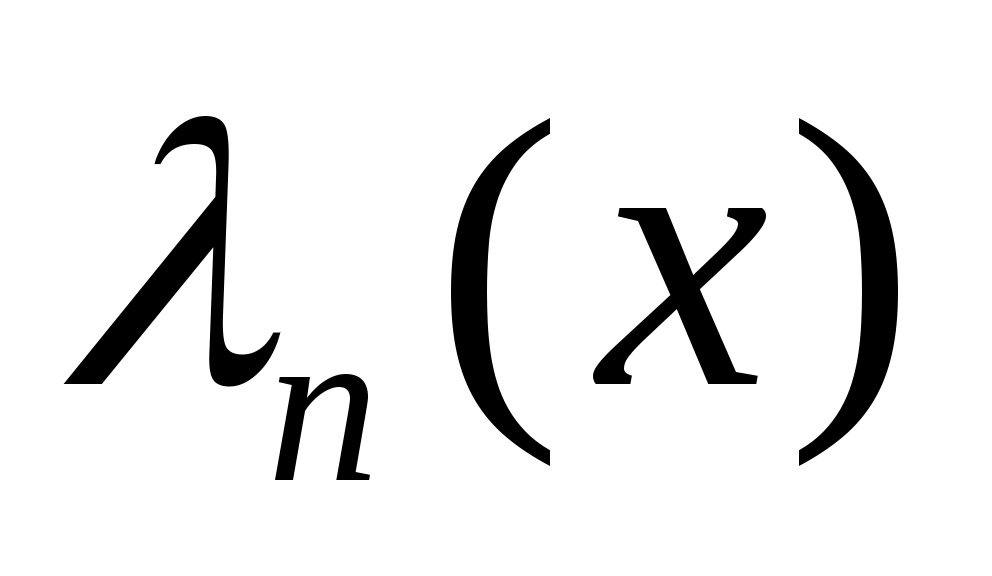 вещественные, различные и расположены на интервале вещественные, различные и расположены на интервале 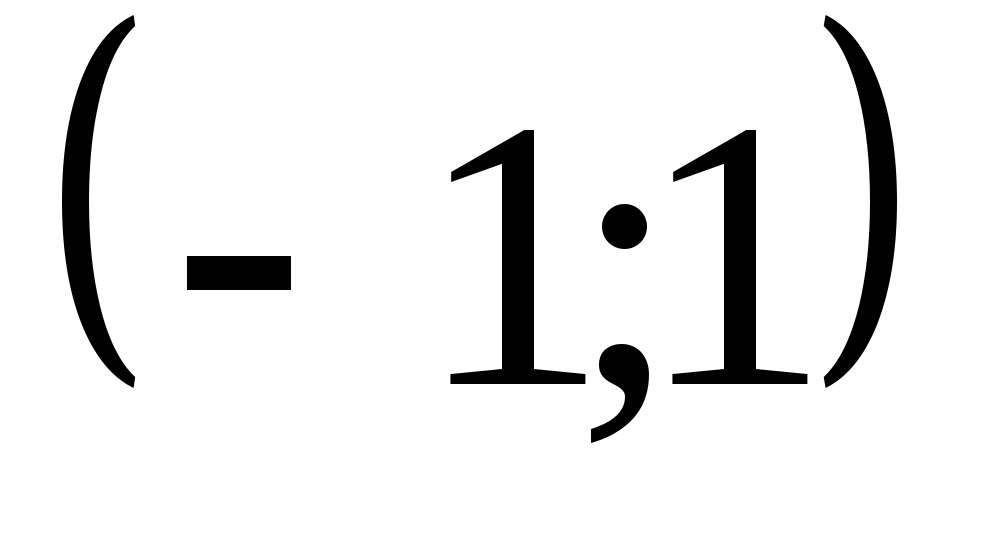 . .
3. Многочлены 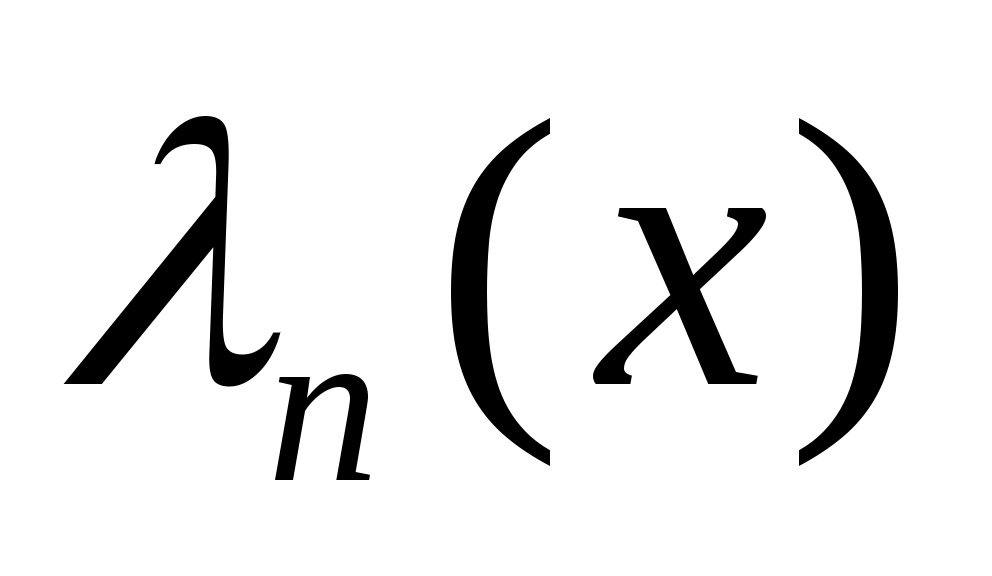 образуют ортогональную систему на образуют ортогональную систему на 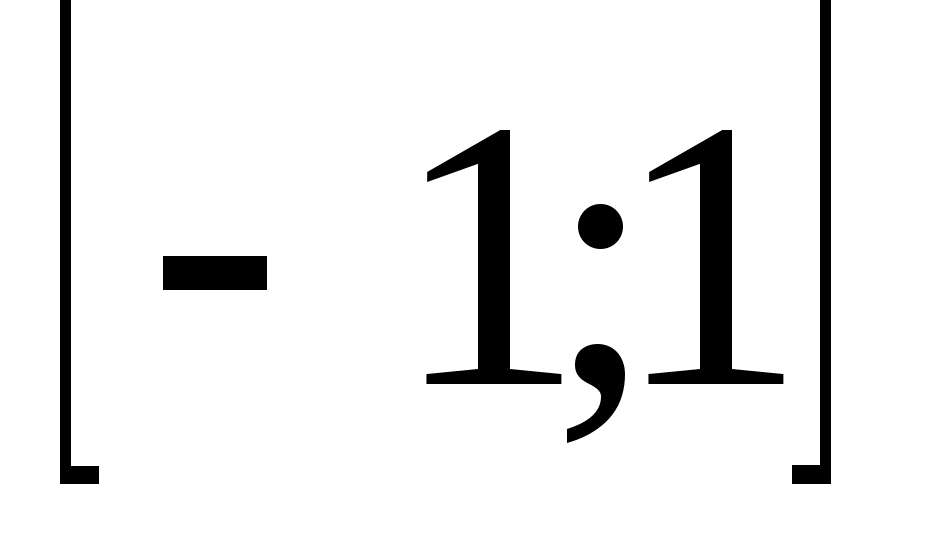 : : 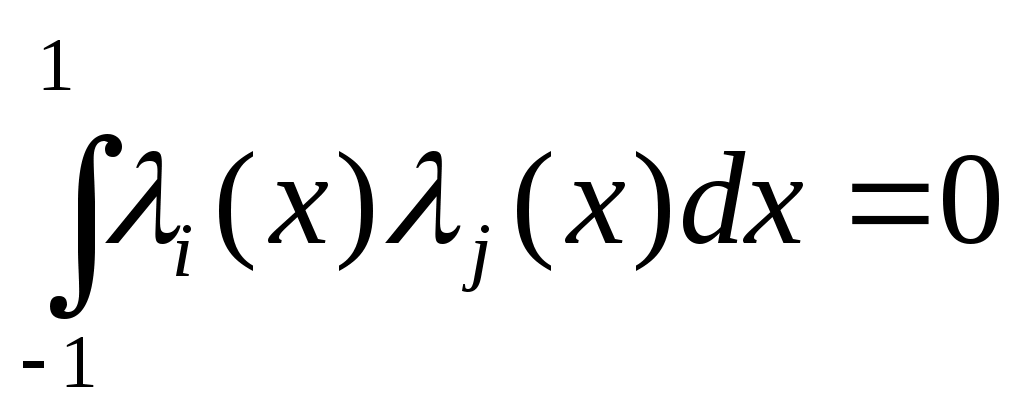 при при 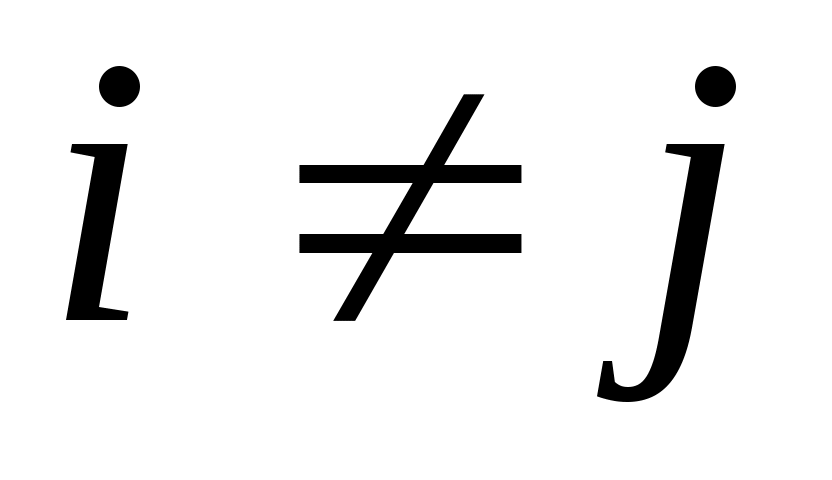 и и 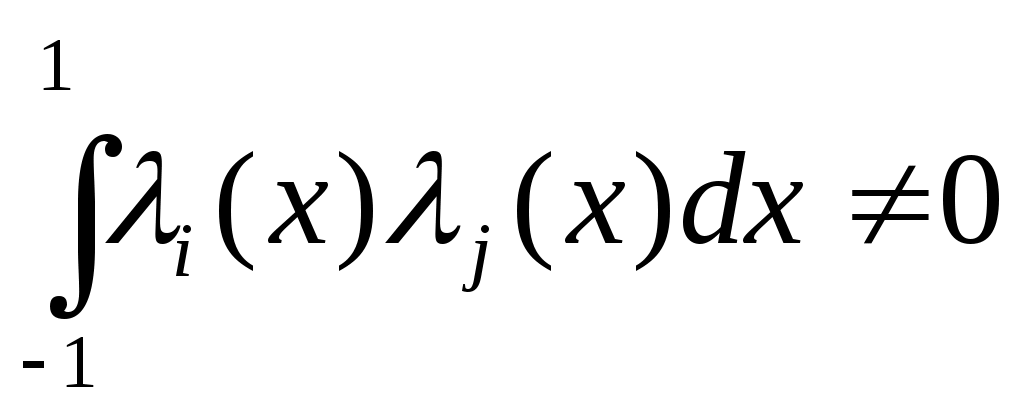 при при 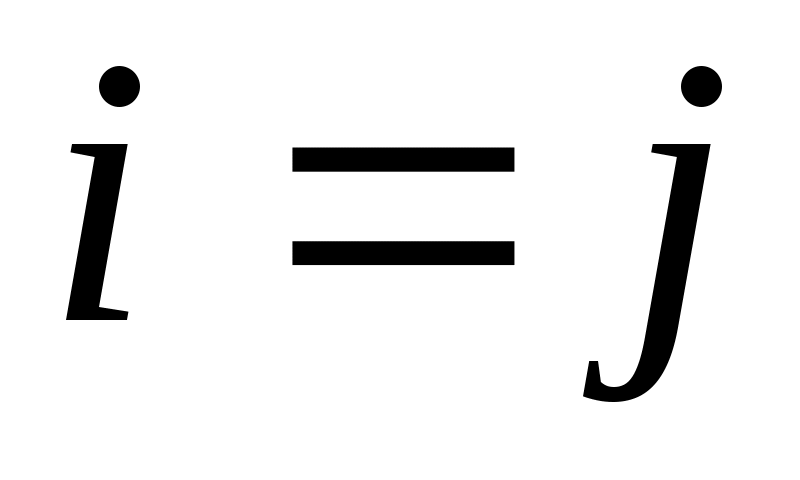 . .
4. Имеет место рекуррентная формула:
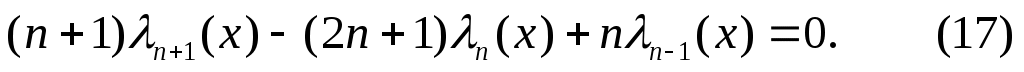
Формула (17) позволяет, используя равенства 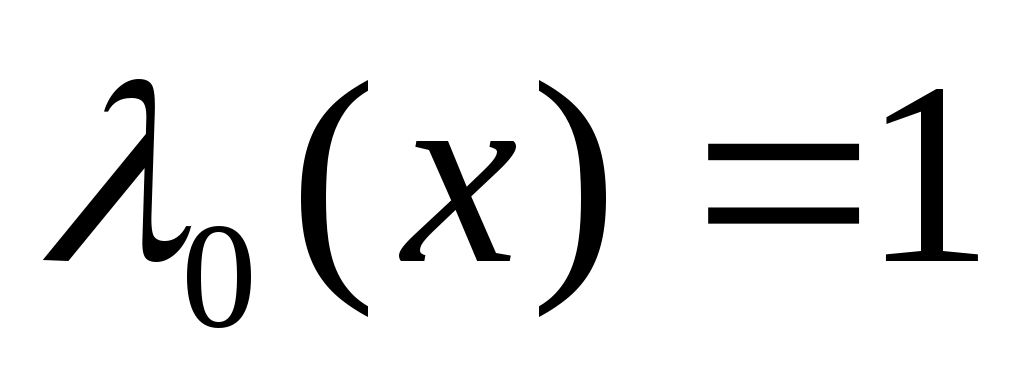 и и 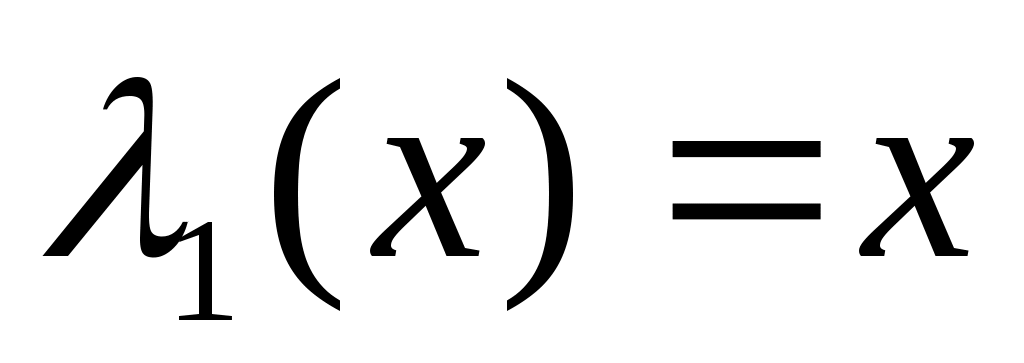 , найти многочлен Лежандра любой степени. , найти многочлен Лежандра любой степени.
Если известны корни 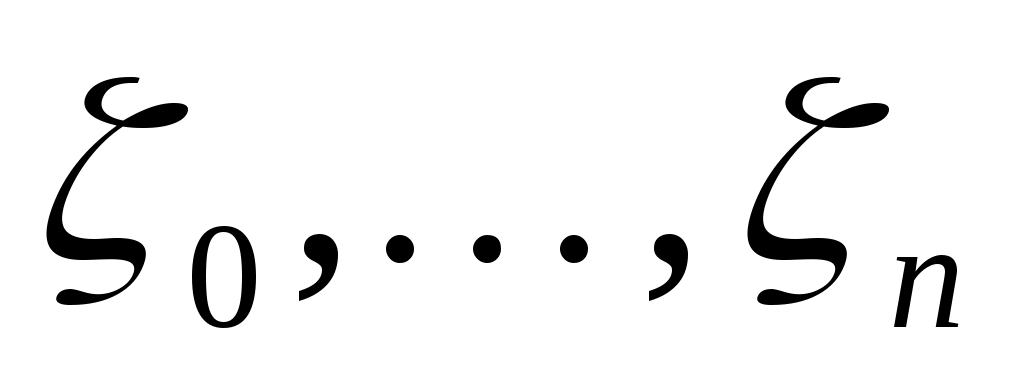 многочлена Лежандра многочлена Лежандра 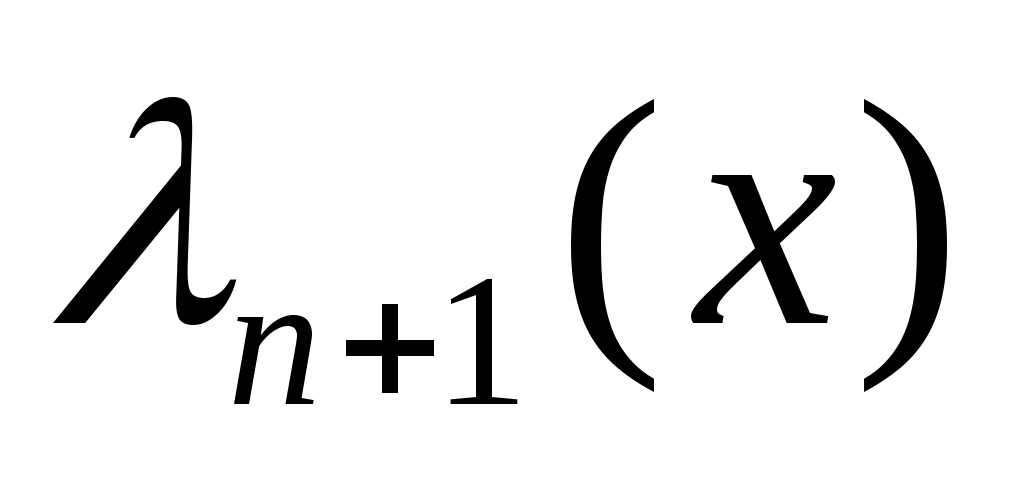 , то, используя (15), получаем квадратурную формулу Гаусса , то, используя (15), получаем квадратурную формулу Гаусса
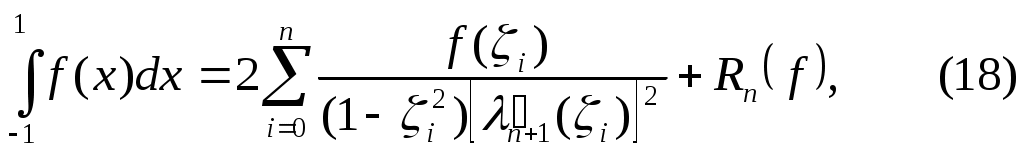
где
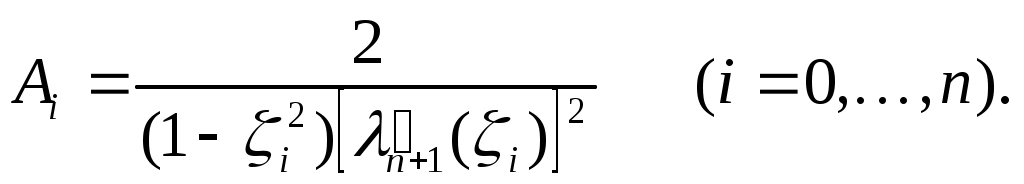
Таблицы узлов и коэффициентов формулы (18) приведены в [3]. Отметим, что корни 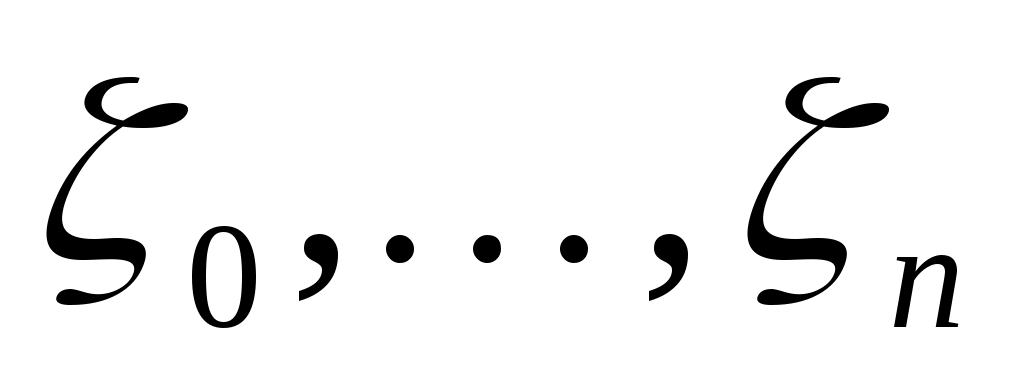 многочленов Лежандра многочленов Лежандра 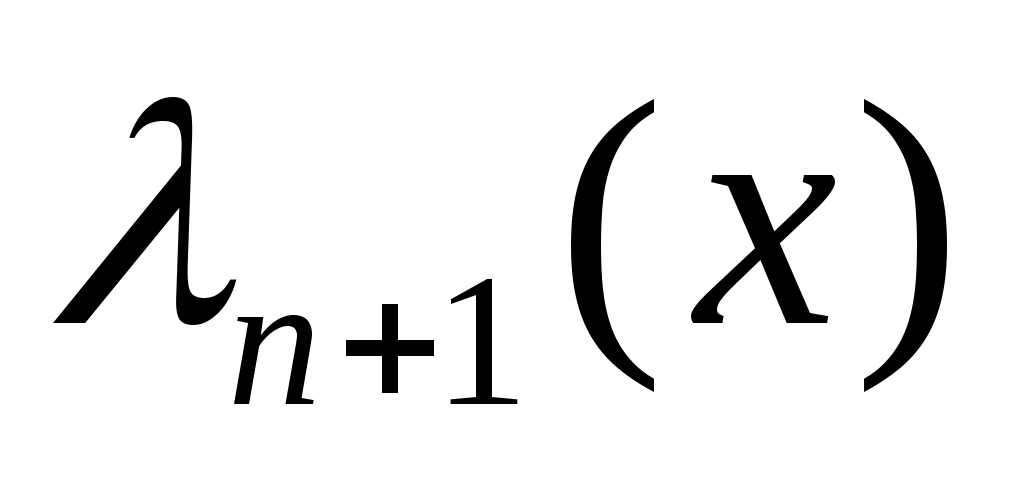 и коэффициенты и коэффициенты 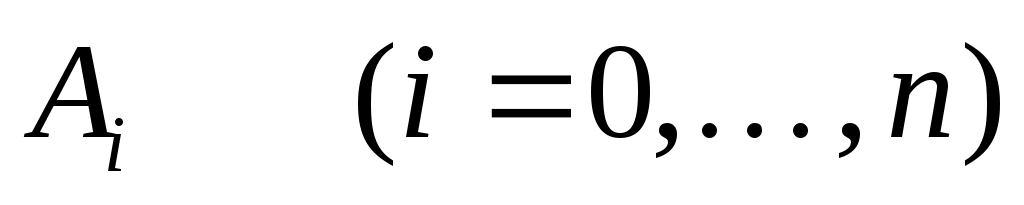 квадратурной формулы (18) обладают симметрией на квадратурной формулы (18) обладают симметрией на 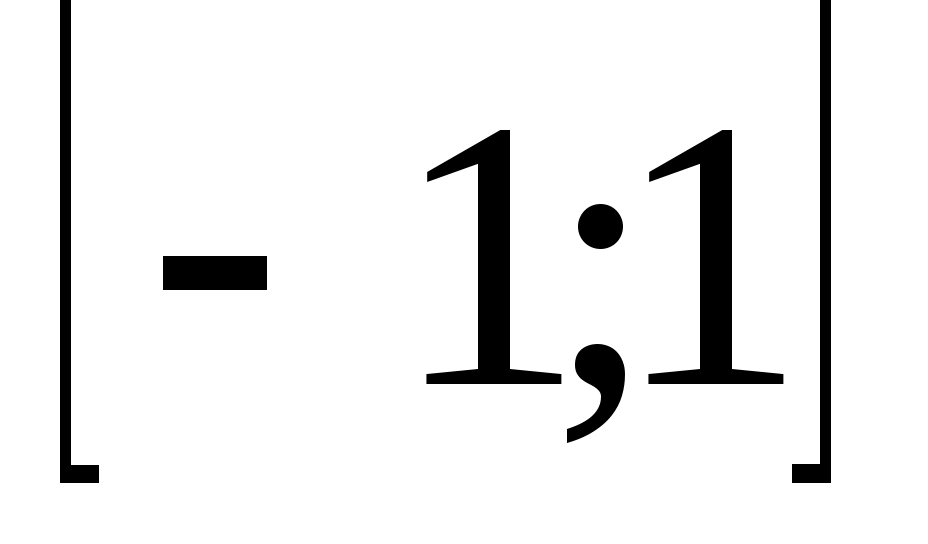 относительно точки относительно точки 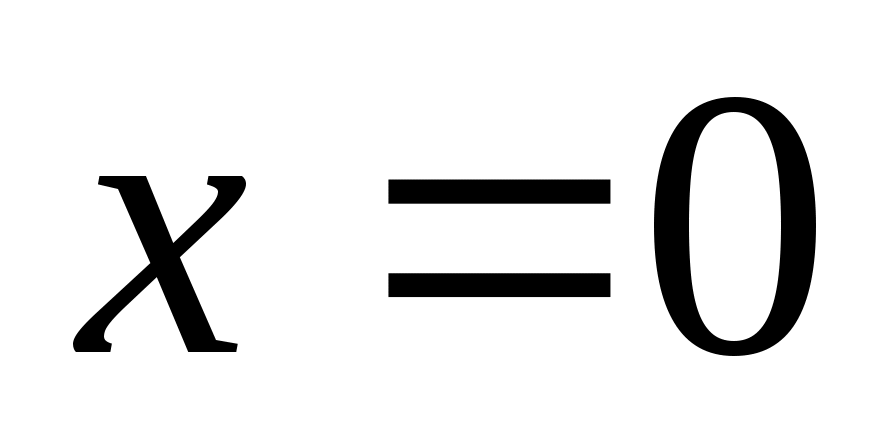 . .
Пересчет узлов и коэффициентов квадратурной формулы на произвольный отрезок 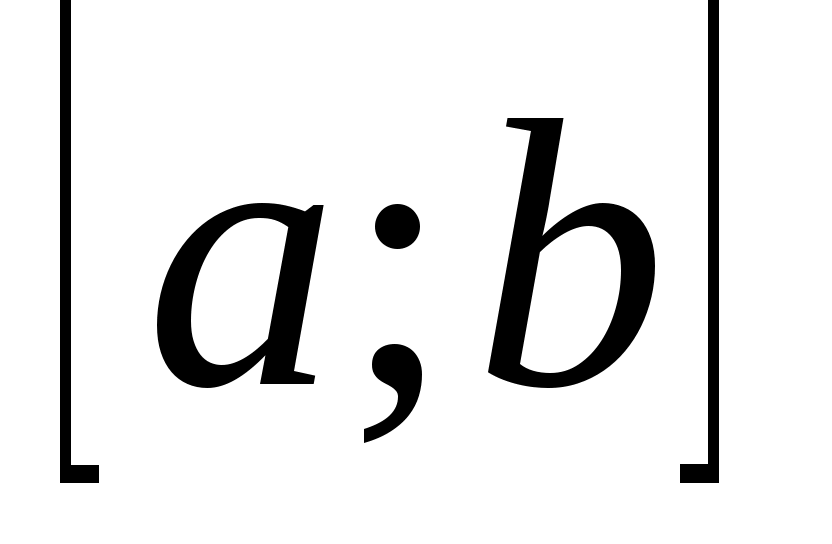 осуществляется с помощью замены переменной осуществляется с помощью замены переменной 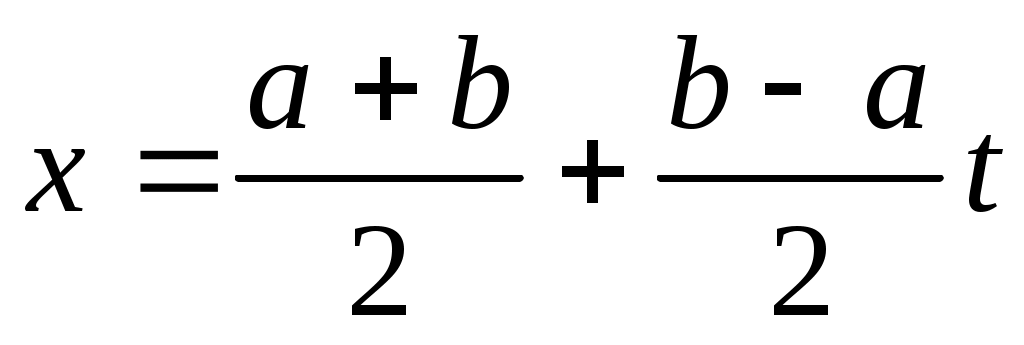 : :
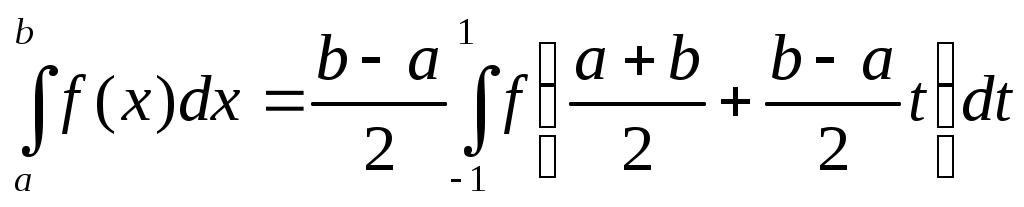
Таким образом, из (18) получаем квадратурную формулу Гаусса для произвольного отрезка 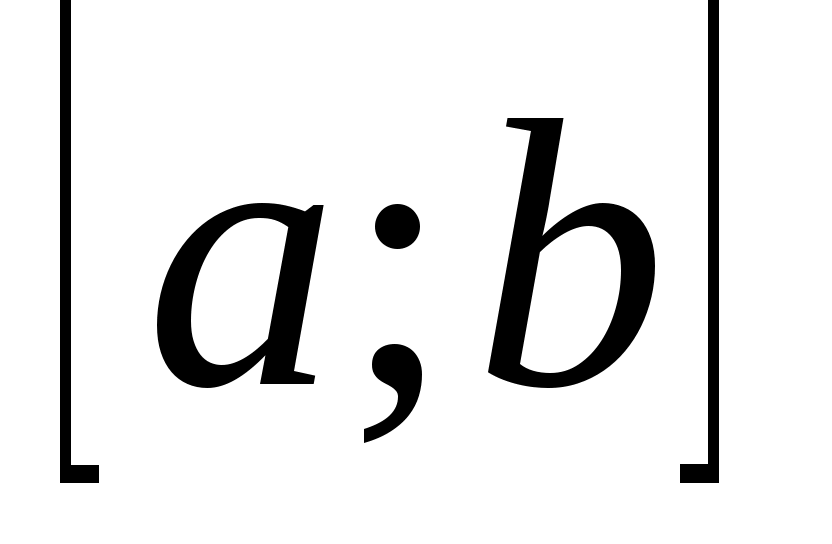
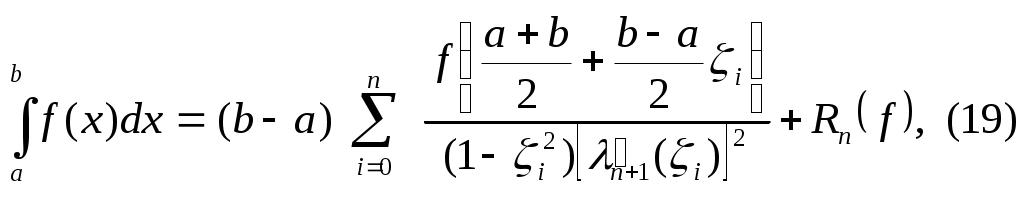
где 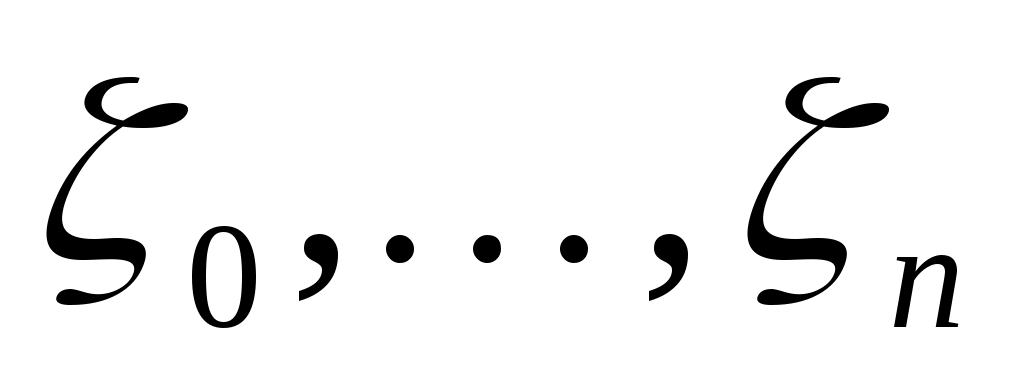 корни многочлена Лежандра корни многочлена Лежандра 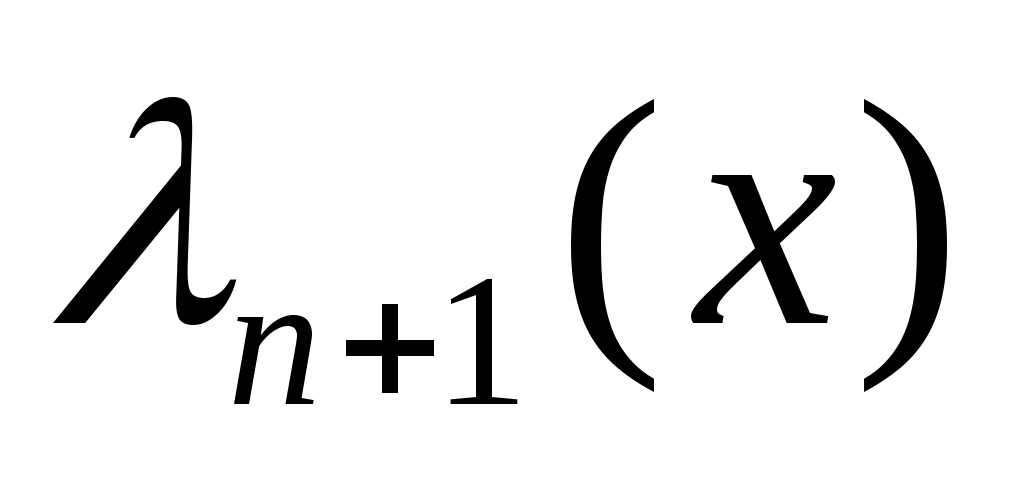 . .
1.6. Квадратурные формулы с весом
Часто удобно исходный интеграл (1) записывать в виде
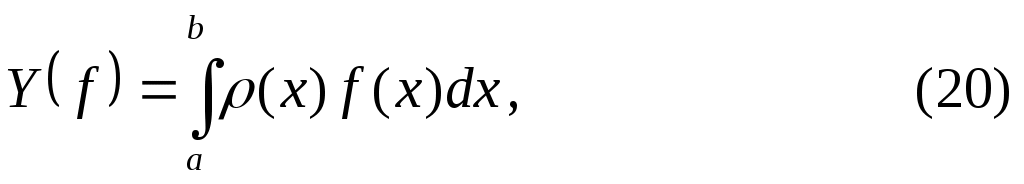
где 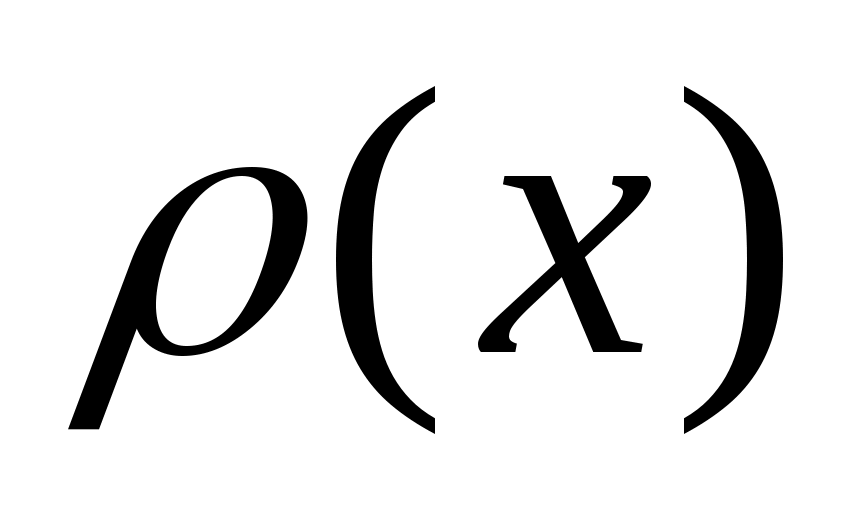 - некоторая заданная функция, называемая весом. Обычно требуют, чтобы интеграл - некоторая заданная функция, называемая весом. Обычно требуют, чтобы интеграл 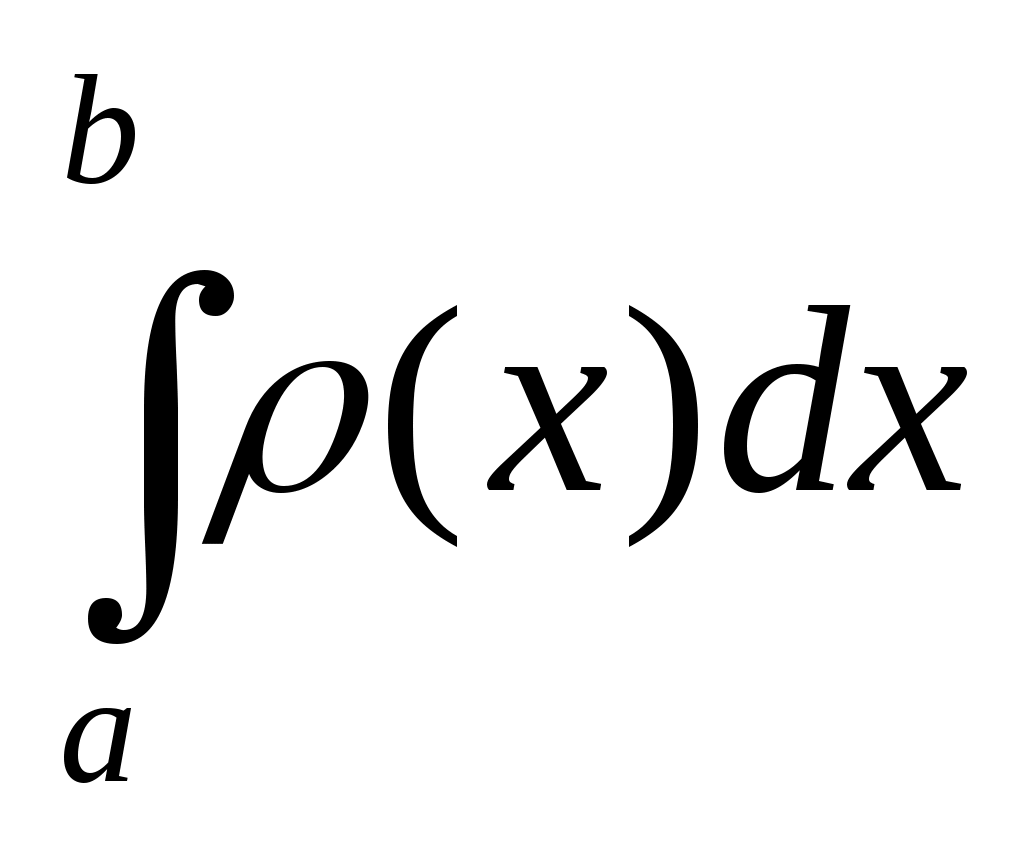 абсолютно сходился и абсолютно сходился и 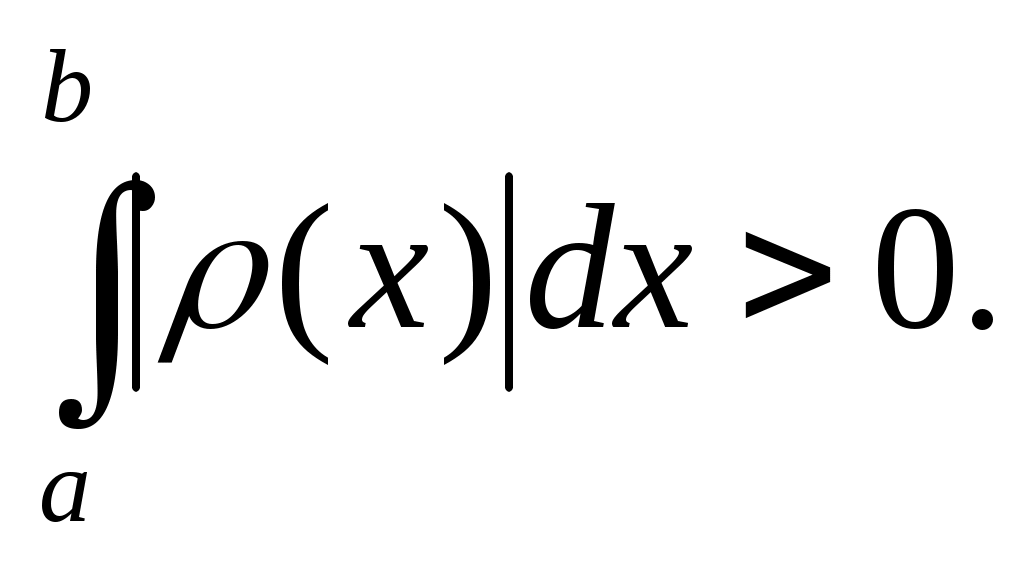 В разложении на множители функции В разложении на множители функции 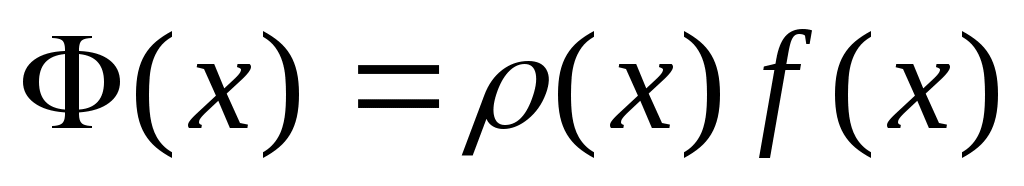 функцию функцию 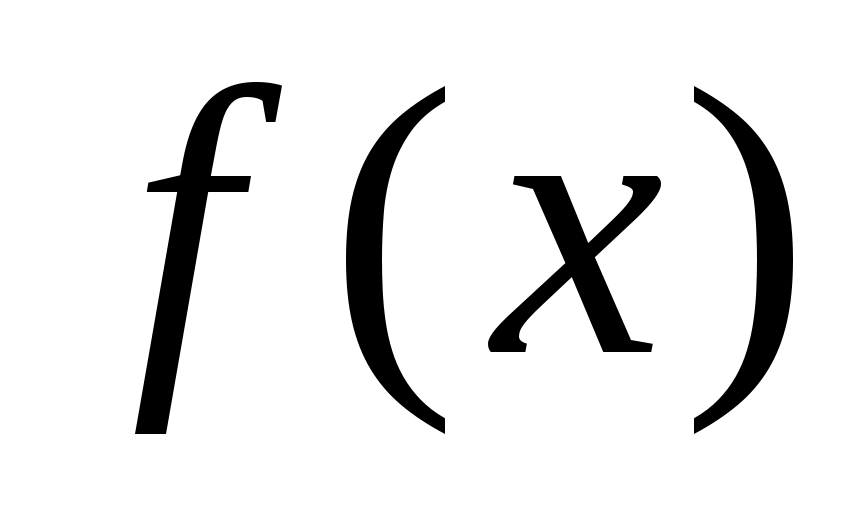 выбирают так, чтобы она обладала достаточно высоким порядком гладкости на выбирают так, чтобы она обладала достаточно высоким порядком гладкости на  , при этом весовая функция , при этом весовая функция 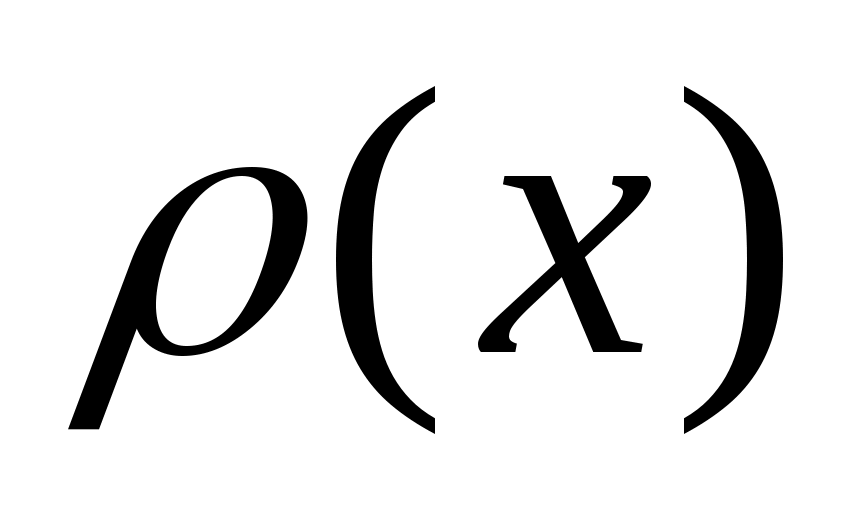 должна содержать все «особенности» подинтегральной функции должна содержать все «особенности» подинтегральной функции 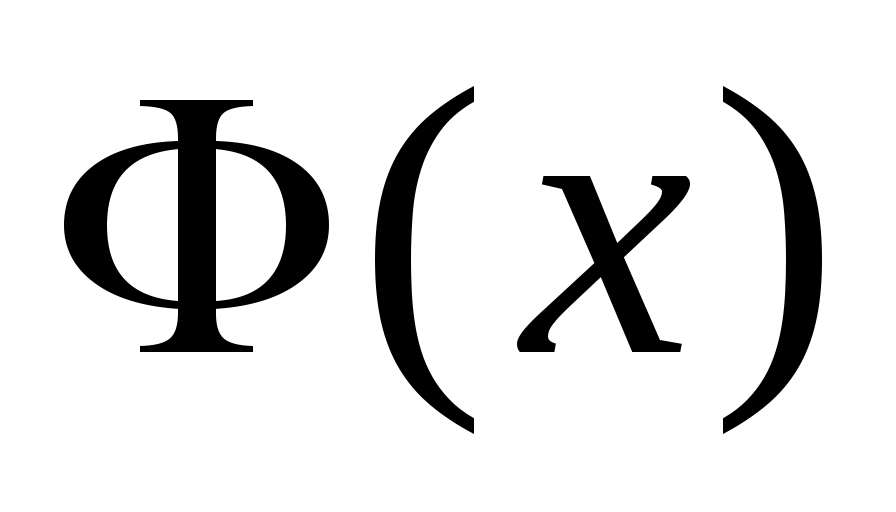 и быть по возможности наиболее простой. и быть по возможности наиболее простой.
В этом случае интерполяционная квадратурная формула (7)-(8) принимает вид
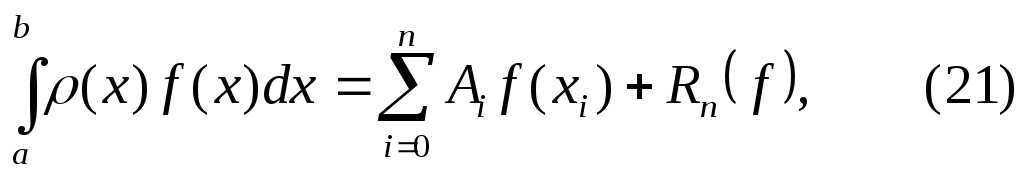
где
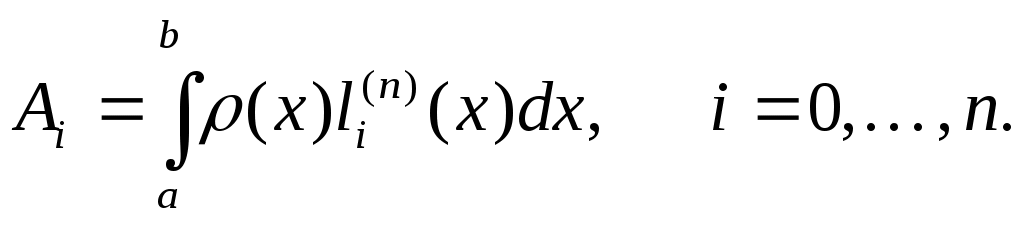
Приведем пример квадратурной формулы Гаусса с весовой функцией Якоби 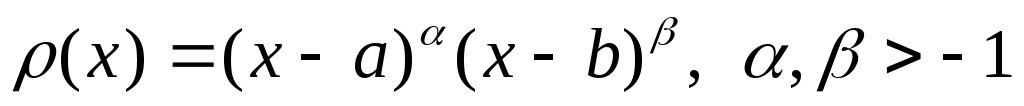 , позволяющей учитывать степенные особенности интегрируемой функции на концах отрезка. Отрезок , позволяющей учитывать степенные особенности интегрируемой функции на концах отрезка. Отрезок 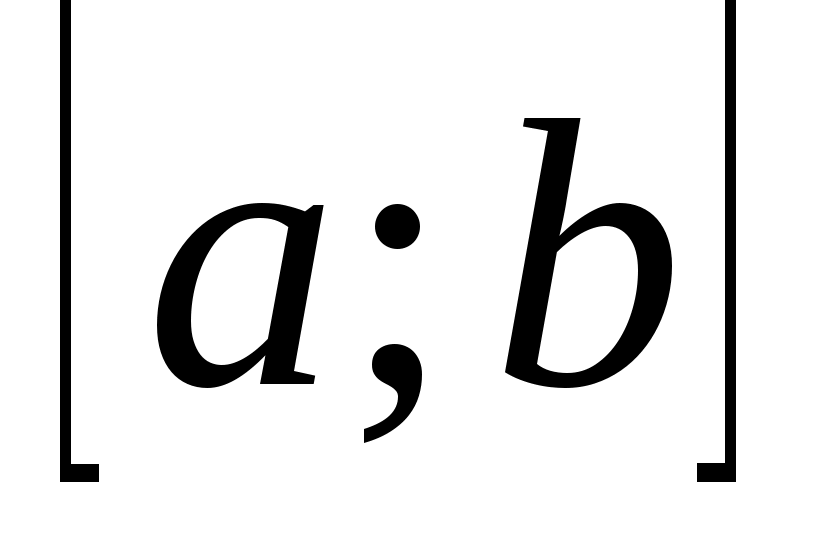 приведем к отрезку приведем к отрезку 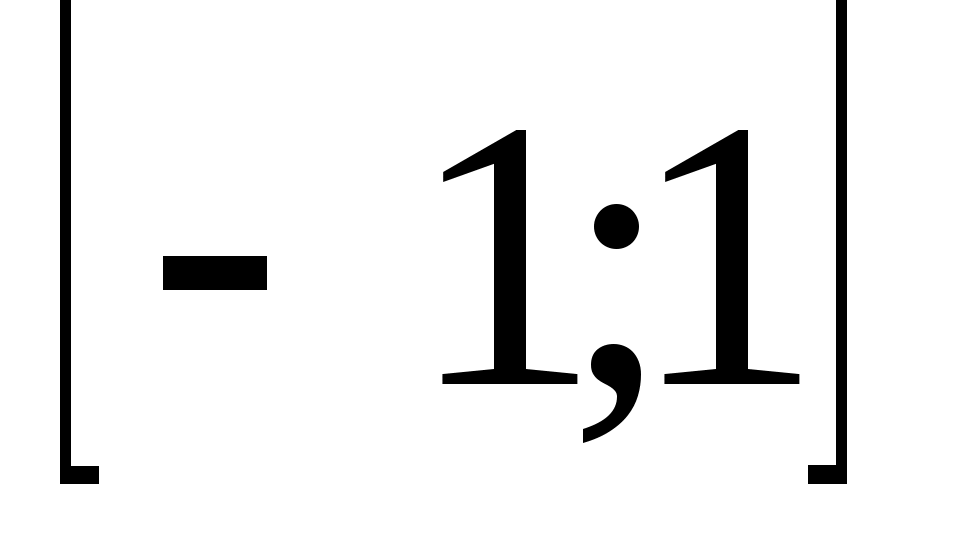 и построим интерполяционную квадратурную формулу и построим интерполяционную квадратурную формулу
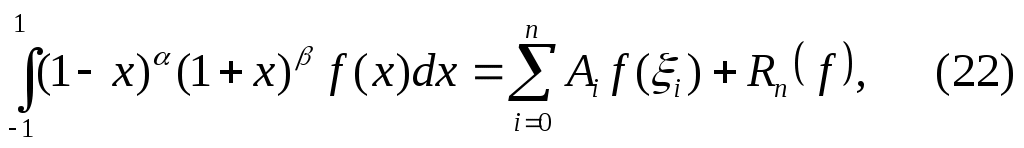
где 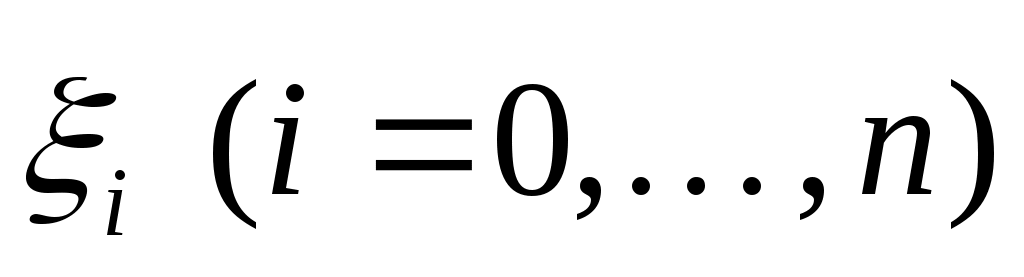 - корни многочлена Якоби - корни многочлена Якоби 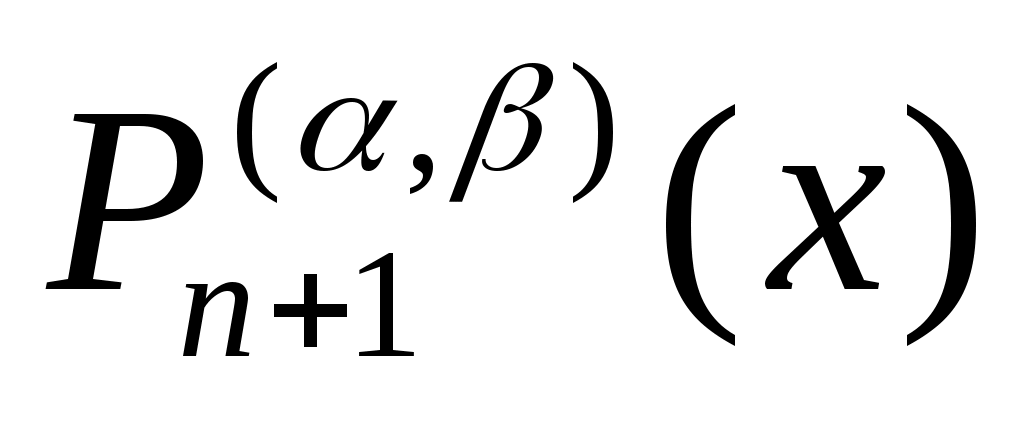 . .
|
|
|
 Скачать 0.92 Mb.
Скачать 0.92 Mb.