чЯч. Учебнометодическое пособие по курсу Методы вычислений для студентов ivv курсов всех форм обучения
 Скачать 0.92 Mb.
|
Многочлен Якоби определяется формулой Многочлены Якоби (23) ортогональны на отрезке  с весом  и для любого многочлена  степени меньшей    С помощью теоремы 3 получаем, что алгебраический порядок точности квадратурной формулы (22) равен  . Квадратурная формула (22) содержит два параметра  и  , из нее могут быть получены специализированные квадратурные формулы, соответствующие распространенным видам степенных особенностей (см. [3]). В справочниках приведены квадратурные формулы Гаусса с другими весами. 1.7. Локально-интерполяционные (составные) квадратурные формулы Для повышения точности квадратурных формул используют прием, идея которого восходит к римановым интегральным суммам. Отрезок интегрирования  разбивают на некоторое число частичных отрезков, на каждом из которых применяют квадратурную формулу с небольшим числом узлов. В качестве параметра квадратурного процесса теперь используют число частичных отрезков.Разобьем отрезок на  частичных отрезков точками  . Для вычисления интеграла на каждом частичном отрезке   применим интерполяционную квадратурную формулу с  узлами  икоэффициентами 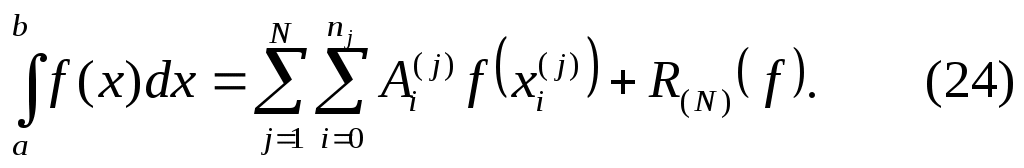  . Получим квадратурную формулу  Пусть 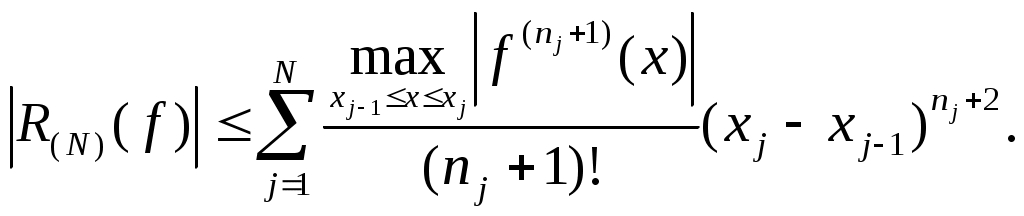 и  , тогда для погрешности квадратурной формулы (24) имеет место оценка Квадратурная формула (24) называется локально-интерполяционной или составной. Наиболее часто формула (24) используется в случае, когда отрезок разбит на частичные отрезки равной длины  и на каждом частичном отрезке используется квадратурная формула Ньютона-Котеса с  узлами. Из (24) получаем при  ,  и   локально-интерполяционную квадратурную формулу где  Сумма абсолютных величин коэффициентов формулы (26)  не зависит от числа частичных отрезков .Оценка погрешности квадратурной формулы (25) имеет вид 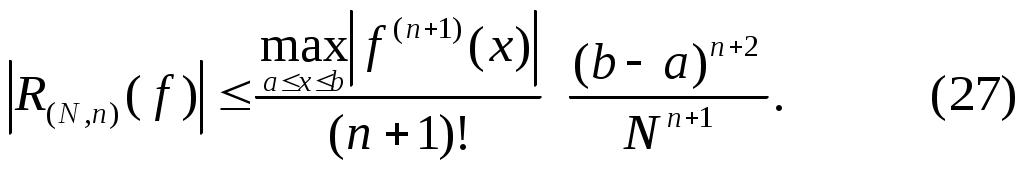 Из теоремы 2 и (27) следует, что квадратурный процесс, порожденный локально-интерполяционной квадратурной формулой (25), является сходящимся при  (со скоростью  на функциях из класса  ). Приведем простейшие составные квадратурные формулы, часто применяемые в практике. Правило трапеций 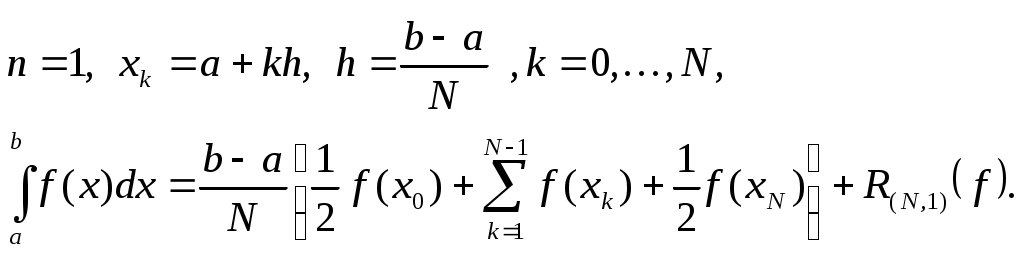 Если  , то  Правило Симпсона (парабол) 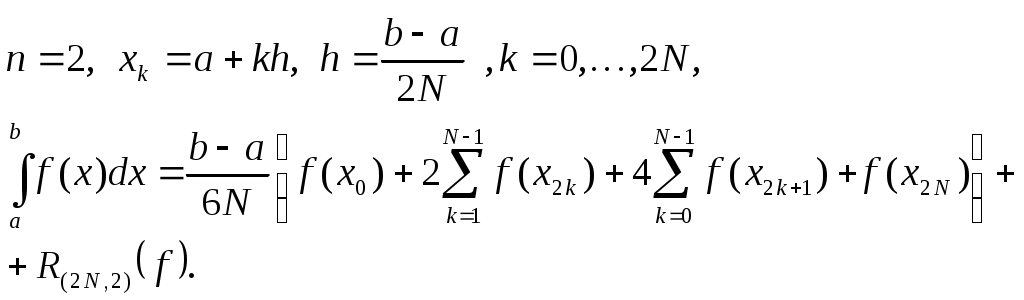 Если  , то  Замечание 5. Алгоритмы численного интегрирования, построенные на основе локально-интерполяционных квадратурных формул (25) имеют существенный недостаток – они насыщаемые. Насыщаемость проявляется в том, что асимптотическое представление погрешности формулы (25) имеет главный член. Отсюда следует неулучшаемость оценки погрешности, сколь бы ни была гладкой функция  .В зависимости от гладкости функции можно выписать любое заданное число членов асимптотического ряда, в который разлагается погрешность  . Рассмотрим конкретный пример – правило трапеций. Если  , то для погрешности квадратурной формулы  имеет место представление  где и  не зависит от  . Из (28) и следует насыщаемость правила трапеций. Классом насыщения в данном случае является пространство  .Имеются простые способы преодоления дефекта локально интерполяционных квадратурных формул – их насыщаемости. Все они основаны на простом соображении, что у соответствующей линейной комбинации двух значений составной квадратурной формулы с различными, но кратными шагами, главный член погрешности исключается. Например, для правила трапеций в силу (28)  , и мы получаем повышение порядка точности, если возьмем линейную комбинацию значений формулы для числа узлов и  соответственно с коэффициентами 1 и – 4.Пусть погрешность локально-интерполяционной квадратурной формулы (25) представима в виде  где и константа  не зависит от . Тогда    Отсюда получаем  и, следовательно, с точностью до  имеем Если  , то Вычисление приближенной оценки погрешности по формуле (29) называется правилом Рунге. Число  в (30) называется уточненным (экстраполированным) по Ричардсону приближенным значением интеграла  (с погрешностью ).Замечание 6. Используя этот прием, можно уничтожить и следующие члены асимптотического разложения погрешности квадратурной формулы. Однако целесообразнее применять квадратурные формулы, сразу приводящие к ненасыщаемым алгоритмам, например, составные формулы Гаусса. Отметим, что составные квадратурные формулы, основанные на формулах Гаусса с достаточно большим числом узлов, дают хорошие результаты как для очень гладких функций, так и для функций невыской гладкости. Замечание 7. Каждая квадратурная формула рассчитывается на определенную гладкость подинтегральной функции. Например, для правила Симпсона погрешность  , если . Если квадратурная формула имеет алгебраический порядок точности  , то при ее применении можно рассчитывать получить «малую погрешность» только в том случае, когда имеет непрерывные производные до порядка, не меньшего . В противном случае погрешность вычисления интеграла может оказаться большой. Для увеличения порядка гладкости подинтегральную функцию представляют в виде двух слагаемых  которые выбирают так, чтобы:  содержала все особенности  или их главную часть и  вычислялся точно;  должна иметь непрерывные производные порядка, большего , для того, чтобы интеграл  можно было вычислить с достаточной точностью с помощью выбранной квадратурной формулы. Приемы разложения (32) для конкретных классов подинтегральных функций изложены в [3].1.8. Задание. Вычислить интеграл  с точностью  , используя правило Симпсона и составную квадратурную формулу Гаусса с пятью узлами. Оценить погрешность используемых квадратурных формул и определить число частичных отрезков разбиения, необходимое для достижения заданной точности вычисления интеграла.Замечание 8. Обычно для вычисления интеграла с точностью  используют итерационный процесс с последовательным удвоением числа частичных отрезков разбиения. Если  , то условием останова процесса является выполнение неравенства  при этом интеграл вычисляется по формуле (31). Варианты заданий
|
