чЯч. Учебнометодическое пособие по курсу Методы вычислений для студентов ivv курсов всех форм обучения

• Название: Учебнометодическое пособие по курсу Методы вычислений для студентов ivv курсов всех форм обучения
• Дата: 11.05.2022
• Размер: 0.92 Mb.
• Имя файла: met_uk4.doc
• Тип: Учебно-методическое пособие; #523486
• страница: 3 из 3

Приложение. Для выполнения задания можно использовать следующие процедуры (на языке Паскаль):
1. Процедура simps, реализующая алгоритм правила Симпсона (парабол):

Procedure simps(a,b:real; var n:longint; var y:real);

{Входные параметры:

a – левый конец отрезка интегрирования;

b – правый конец отрезка интегрирования;

n - число частичных отрезков разбиения.

Выходные параметры:

y – значение интеграла.

Здесь f имя функции, вычисляющей значения подинтегральной функции.}

var

i :longint;

h,x :real;

begin

h:=(b-a)/n; y:=0; x:=a;

for i:=1 to n do

begin y:=y+f(x)+4*f(x+0.5*h)+f(x+h); x:=x+h end;

y:=y*h/6

end;

2. Процедура gauss, реализующая алгоритм составной формулы Гаусса с пятью узлами:

Procedure gauss(a,b:real; var n:word; var y:real);

{Входные параметры:

a – левый конец отрезка интегрирования;

b – правый конец отрезка интегрирования;

n - число частичных отрезков разбиения.

Выходные параметры:

y – значение интеграла.

Здесь f – имя функции, вычисляющей значения подинтегральной функции;

vec – одномерный массив (type vec=array[1..5]of real).}

var

i,j :word;

h,x,x1 :real;

ag,xg :vec;

z :real;

begin

ag[1]:=0.2369268850; xg[1]:=-0.9061798459;

ag[2]:=0.4786286705; xg[2]:=-0.5384693101;

ag[3]:=0.5688888889; xg[3]:=0.0;

ag[4]:=ag[2]; xg[4]:=-xg[2];

ag[5]:=ag[1]; xg[5]:=-xg[1];

h:=(b-a)/n; z:=0; x1:=a+0.5*h;

for j:=1 to n do

begin

for i:=1 to 5 do

begin x:=x1+0.5*h*xg[I]; z:=z+ag[i]*f(x); end;

x1:=x1+h

end;

y:=z*0.5*h

end;

II. Численное дифференцирование

2.1. Постановка задачи. Применение интерполяционного многочлена Лагранжа

Пусть на отрезке R определена достаточно гладкая функция и требуется вычислить в точке ее производную . Если функция задана таблично или имеет сложное аналитическое выражение, то непосредственное дифференцирование невозможно. Поэтому строят приближенные формулы численного дифференцирования.

Один из универсальных способов конструирования формул численного дифференцирования состоит в том, что по функции и узлам строят интерполяционный многочлен Лагранжа (6) и полагают



Разность



называется погрешностью формулы численного дифференцирования (33).

Для получения оценок погрешности формулы (33) для заданного существования производной недостаточно. Обычно требуется выполнение условия , .

Замечание 9. Для конструирования формул численного дифференцирования можно также использовать интерполяционные сплайны. В вычислительной практике для вычисления и обычно используют интерполяционный естественный кубический сплайн :

Приведем простейшие формулы численного дифференцирования.

1)



Если , то

2)



Если , то

3)



Если , то

Представления погрешности (34) формулы численного дифференцирования (33), выражаемые через производные функции , удается найти только в частных случаях. Общая оценка погрешности формулы (33) определяется следующей теоремой.

Теорема 4. Пусть 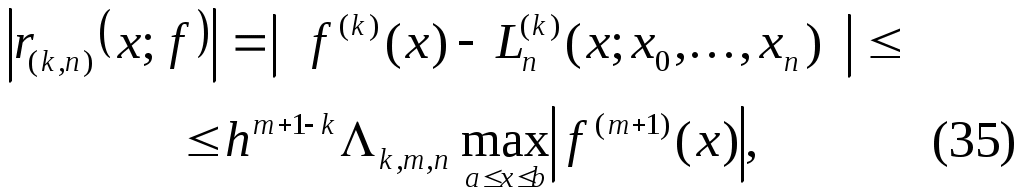, . Тогда существуют такие константы , зависящие только от и независящие от шага и функции , что



где - интерполяционный многочлен Лагранжа (6) и .

Замечание 10. Оценка (35) с постоянными сильно завышена и редко используется на практике. Однако оценка (35) полезна тем, что она устанавливает скорость убывания погрешности относительно шага на всем отрезке при фиксированных значениях параметров ( ). Шаг является основным параметром, которым распоряжается вычислитель.
2.2. Сходящиеся формулы численного дифференцирования

Пусть гладкая на некотором интервале D вещественной прямой R функция и требуется вычислить производную . Построим сетку Рассмотрим формулу численного дифференцирования



где R, .

Разность



называется погрешностью формулы численного дифференцирования (36).
Формула численного дифференцирования (36) называется сходящейся, если при для любой функции (в любой точке гладкости функции ).
Будем говорить, что формула (36) аппроксимирует с порядком (имеет - ый порядок точности), если при .

Функцию комплексного переменного С вида



назовем характеристической функцией (символом) формулы численного дифференцирования (36).
Теорема 5. Формула численного дифференцирования (36) является сходящейся тогда и только тогда, когда ее характеристическая функция представима в виде


Замечание 11 . В представлении (38) характеристической функции сходящейся формулы численного дифференцирования множитель



имеет корней; они называются характеристическими числами сходящейся формулы численного дифференцирования (характеристические числа отличны от 1).

Для построения формулы численного дифференцирования, имеющей - ый порядок точности, можно воспользоваться методом неопределенных коэффициентов.

Теорема 6. Для того чтобы формула численного дифференцирования (36) аппроксимировала 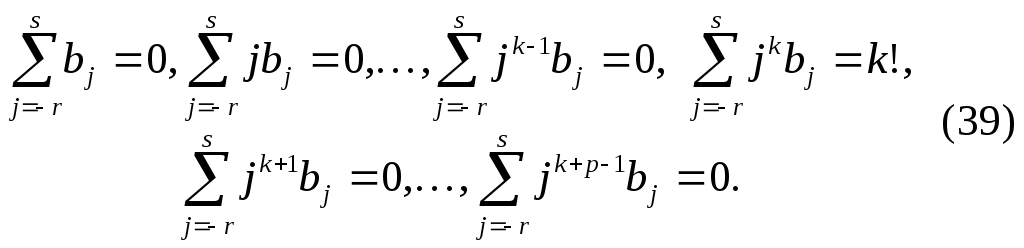с порядком , необходимо и достаточно, чтобы ее коэффициенты являлись решением системы линейных уравнений

Система (39) содержит уравнений относительно неизвестных .

Из теоремы 6 следует, что для построения искомой формулы численного дифференцирования (36) нужно найти решение системы (39). Выберем 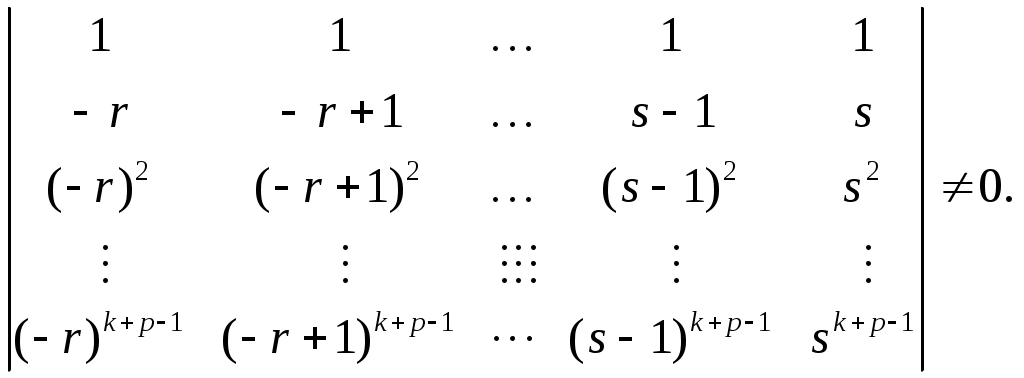и так, чтобы . В этом случае определитель системы (39) есть определитель Вандермонда и отличен от нуля:


Таким образом, для любых и можно построить формулу численного дифференцирования, аппроксимирующую с порядком .
2.3. Задание. Для заданных и методом неопределенных коэффициентов построить формулу численного дифференцирования, аппроксимирующую с порядком .


Составитель Трофимов Валерий Павлович
Редактор Тихомирова О.А.