ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014. Учебное пособие для 1го курса оглавление Оглавление 2 основы программирования 2 Введение 2

• Название: Учебное пособие для 1го курса оглавление Оглавление 2 основы программирования 2 Введение 2
• Анкор: ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014.doc
• Дата: 20.04.2018
• Размер: 4.81 Mb.
• Имя файла: ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014.doc
• Тип: Учебное пособие; #18298
• страница: 11 из 17

3.11. Цикл по параметру

Рассмотрим следующую простую задачу: требуется вычислить сумму целых чисел от M до N путем прямого суммирования. Здесь М и N — целые числа. Задачу можно сформулировать так: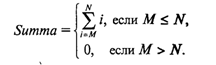



Алгоритм и программа решения этой задачи с использованием структуры цикл-пока представлены на рис. 23.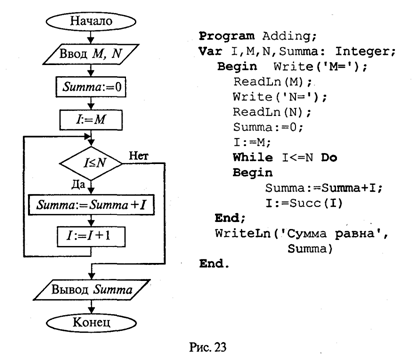



А теперь введем новый тип циклической структуры, который будет называться цикл по параметру, или цикл-для. Блок-схема и программа на Паскале для решения рассматриваемой задачи с использованием этой структуры приведены на рис. 24.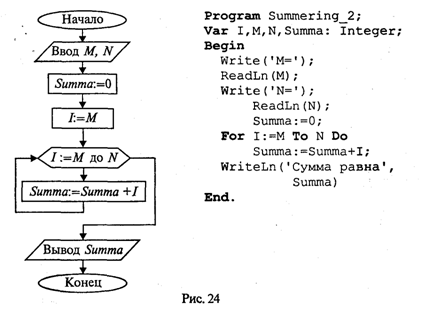



Здесь целая переменная I последовательно принимает значения в диапазоне от М до N. При каждом значении I выполняется тело цикла. После последнего выполнения цикла при I = N происходит выход из цикла на продолжение алгоритма. Цикл выполняется хотя бы один раз, если М ≤ N, и не выполняется ни разу при М > N.

В программе используется оператор цикла For, синтаксическая диаграмма которого представлена на рис. 25.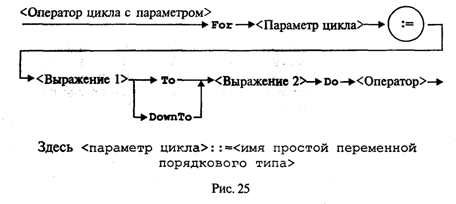



Выполнение оператора For в первом варианте (То) происходит по следующей схеме:

1. Вычисляются значения < Выражения 1> и < Выражения 2>. Это делается только один раз при входе в цикл.

2. Параметру цикла присваивается значение < Выражения 1>.

3. Значение параметра цикла сравнивается со значением < Выражения 2 >. Если параметр цикла меньше или равен этому значению, то выполняется тело цикла, в противном случае выполнение цикла заканчивается.

4. Значение параметра цикла изменяется на следующее значение в его типе (для целых чисел — увеличивается на единицу); происходит возврат к пункту 3.

Оператор цикла For объединяет в себе действия, которые при использовании цикла While выполняют различные операторы: присваивание параметру начального значения, сравнение с конечным значением, изменение на следующее.

Как известно, результат суммирования целых чисел не зависит от порядка суммирования. Например, в рассматриваемой задаче числа можно складывать и в обратном порядке, т.е. от N до М (N ≥ М). Для этого можно использовать второй вариант оператора цикла For:

Summa:=0 ;

For I:=N DownTo M Do

Summa:=Summa+I;

Слово DownTo буквально можно перевести как «вниз до». В таком случае параметр цикла изменяется по убыванию, т.е. при каждом повторении цикла параметр изменяет свое значение на предыдущее (равносильно i:=pred(i)). Тогда ясно, что цикл не выполняется ни разу, если N < М.

Работая с оператором For, учитывайте следующие правила:

• параметр цикла не может иметь тип Real;

• в теле цикла нельзя изменять переменную «параметр цикла»;

• при выходе из цикла значение переменной-параметра является неопределенным.

В следующем примере в качестве параметра цикла For используется символьная переменная. Пусть требуется получить на экране десятичные коды букв латинского алфавита. Как известно, латинские буквы в таблице кодировки упорядочены по алфавиту. Вот фрагмент такой программы:

For С:='а' То 'z' Do

Write (С,'-',Ord(C));

Здесь переменная С имеет тип Char.

3.12. Особенности целочисленной и вещественной арифметики

Числовые расчеты могут производиться на множестве целых чисел или на множестве вещественных чисел. С математической точки зрения целые числа являются подмножеством множества вещественных чисел. Поэтому, казалось бы, можно было бы и не разделять числа на целые и вещественные и иметь дело только с вещественным числовым типом данных.

Однако целочисленная арифметика на ЭВМ имеет три очень существенных преимущества по сравнению с вещественной арифметикой:

• 
  целые числа всегда представимы своими точными значениями;
  
• 
  операции целочисленной арифметики дают точные результаты;
  
• 
  операции целочисленной арифметики выполняются быстрее, чем операции вещественной («плавающей») арифметики.
  

Недостатком целого типа данных является сравнительно узкий диапазон допустимых значений (для типа Integer — от -32768 до 32767). При исполнении программы автоматически не контролируется выход значения целой величины за эти границы. В этом случае получается ошибочный результат. Если такая опасность существует, то программист должен сам предусматривать в своей программе предупреждение целочисленного переполнения. Чаще всего целый тип используется для представления счетчиков, номеров, индексов и других целочисленных величин.

Вам уже известно, что целый тип данных является порядковым. Вспомним, что это значит:

• 
  величины этого типа принимают конечное множество значений, которые могут быть пронумерованы;
  
• 
  на множестве значений данного типа работают понятия: «предыдущий элемент», «последующий элемент».
  

Почему же вещественный тип данных не является упорядоченным? Вещественные числа в памяти ЭВМ представляются в формате с плавающей точкой, т.е. в виде совокупности пары чисел — целого порядка и нормализованной мантиссы. Поскольку размер ячейки памяти ограничен, в большинстве случаев мантисса оказывается «обрезанной», иными словами, приближенной. Точное представление в памяти имеет лишь дискретное конечное множество вещественных значений. Поэтому множество вещественных чисел в машинном представлении (рис. 26) есть дискретное, конечное множество, хотя оно и является отражением континуума действительных чисел.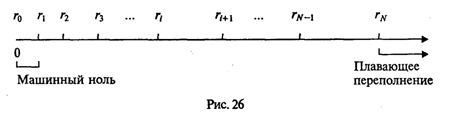



На рисунке изображена положительная часть действительной числовой оси, на которой штрихами отмечены значения, точно представимые в вещественном типе данных. Эта картина симметрично отражается на отрицательную полуось.

С ростом абсолютного значения интервал между соседними точками растет. Он равен (при двоично-нормализованной форме с плавающей точкой) 2-t х 2p = 2p-t, где р — порядок числа, a t — количество двоичных разрядов в мантиссе. Ясно, что с ростом абсолютной величины числа его порядок (р) растет и, следовательно, растет шаг между двумя соседними значениями. Минимальный шаг



максимальный шаг



Например, если рmin = -64; рmax = 63; t = 24, то имеем Δrmin = 2-88; Δrmax   = 239.

Казалось бы, значения множества точно представимых вещественных чисел можно пронумеровать и таким образом определить на нем понятия «следующий», «предыдущий». Однако расстояние между двумя последовательными значениями на этом множестве оказывается величиной субъективной, в частности, зависящей от размера ячейки памяти, в которой хранится число. Например, если под мантиссу выделяется 3 байта, то следующее значение получается путем прибавления к мантиссе единицы в 24-м разряде; если 5 байт — единицы в 40-м разряде.

Бесконечное количество действительных чисел вообще непредставимо точно в памяти ЭВМ. Если вещественное значение X попадает между двумя точно пред ставимыми значениями ri и ri+1, то оно заменяется на значение меньшего по модулю из этой пары чисел (некоторые типы процессоров выполняют «правильное» округление). Следовательно, в общем случае вещественные числа хранятся в памяти приближенно, т.е. несут в себе погрешность, которая называется погрешностью машинного округления.

Из сказанного следует, что если два числа X и Y удовлетворяют условиям ri < X < ri+1; ri < Y < ri+1, но Х ≠ Y, то в машинном представлении они неразличимы.

Разность между вещественной единицей и ближайшим к ней числом, представимым в памяти машины, называется машинным эпсилон ε. Иначе говоря, если ri = 1, то ri+1= 1 + ε. Легко понять, что величина машинного ε связана только с разрядностью мантиссы в представлении вещественных чисел на данной ЭВМ.

Для определения величины машинного ε можно использовать следующую программу:

Program EpsiIon;

Var Eps: Real;

Begin Eps:=1/2;

While 1.0+Eps>l.0 Do

Eps:=Eps/2;

WriteLn('Машинный эпсилон=',Eps)

End.