ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014. Учебное пособие для 1го курса оглавление Оглавление 2 основы программирования 2 Введение 2

• Название: Учебное пособие для 1го курса оглавление Оглавление 2 основы программирования 2 Введение 2
• Анкор: ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014.doc
• Дата: 20.04.2018
• Размер: 4.81 Mb.
• Имя файла: ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014.doc
• Тип: Учебное пособие; #18298
• страница: 12 из 17

3.13. Подпрограммы

С понятием вспомогательного алгоритма вы уже знакомы (см. разд. 1.4). В языках программирования вспомогательные алгоритмы называются подпрограммами. В Паскале различаются две разновидности подпрограмм: процедуры и функции. Рассмотрим этот вопрос на примере следующей задачи: даны два натуральных числа a и b. Требуется определить наибольший общий делитель трех величин: а + b, |а – b|, а • b. Запишем это так: НОД (a + b, |а – b|, а • b).

Идея решения состоит в следующем математическом факте: если х, у, z — три натуральных числа, то НОД(х, у, z) = НОД(НОД(х, у), z). Иначе говоря, нужно найти НОД двух величин, а затем НОД полученного значения и третьего числа (попробуйте это доказать).

Очевидно, что вспомогательным алгоритмом для решения поставленной задачи является алгоритм получения наибольшего общего делителя двух чисел. Эта задача решается с помощью известного алгоритма Евклида (см. раздел 1.3). Запишем его в форме процедуры на алгоритмическом языке.

Процедура Евклид(цел M,N,K);

нач

пока M<>N

нц

если M>N

то M:=M-N

иначе N:=N-M

кв

кц;

K:=M

кон

Здесь M и N являются формальными параметрами процедуры. M и N параметры-аргументы, K — параметр-результат. Основной алгоритм, решающий исходную задачу, будет следующим:

алг задача;

цел а,b,с;

нач ввод(а,b);

Евклид(а+b,|a-b|,с);

Евклид(с,а*b,с);

вывод(с)

кон.

Процедуры в Паскале. Основное отличие процедур в Паскале от процедур в Алгоритмическом языке (АЯ) состоит в том, что процедуры в Паскале описываются в разделе описания подпрограмм, а в АЯ процедура является внешней по отношению к вызывающей программе. Теперь посмотрим, как решение поставленной задачи программируется на Турбо Паскале.

Program NOD1;

Var А,В,С: Integer;

Procedure Evklid(M,N: Integer; Var К: Integer);

Begin

While M<>N Do

If M>N

Then M:=M-N

Else N:=N-M;

K:=M

End;

Begin

Write('a=');

ReadLn(A) ;

Write('b=');

ReadLn(B);

Evklid(A+B,Abs(A-B),C);

Evklid(C,A*B,C);

WriteLn('НОД=',C)

End.

В данном примере обмен аргументами и результатами между основной программой и процедурой производится через параметры (формальные и фактические). Существует и другой механизм обмена — через глобальные переменные. А сейчас рассмотрим синтаксическую диаграмму описания процедуры (рис. 27).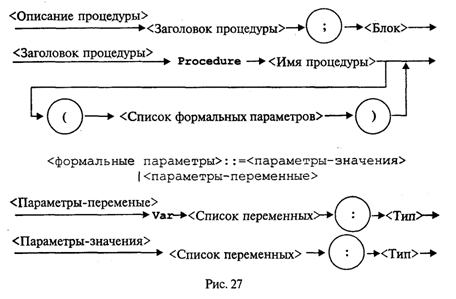



Из диаграммы видно, что процедура может иметь параметры, а может быть и без них .

Чаще всего аргументы представляются как параметры-значения (хотя могут быть и параметрами-переменными). А для передачи результатов используются параметры-переменные.

Процедура в качестве результата может передавать в вызывающую программу множество значений (в частном случае — одно), а может и ни одного. Теперь рассмотрим правила обращения к процедуре. Обращение к процедуре производится в форме оператора процедуры (рис. 28).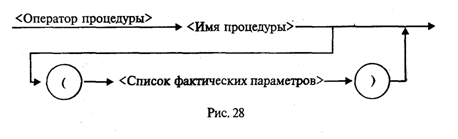



Если описана процедура с формальными параметрами, то и обращение к ней производится оператором процедуры с фактическими параметрами. Правила соответствия между формальными и фактическими параметрами: соответствие по количеству, соответствие по последовательности и соответствие по типам.

Первый вариант взаимодействия формальных и фактических параметров называется передачей по значению: вычисляется значение фактического параметра (выражения) и это значение присваивается соответствующему формальному параметру. Второй вариант взаимодействия называется передачей по имени: при выполнении процедуры имя формальной переменной заменяется на имя соответствующей фактической переменной (в откомпилированной программе имени переменной соответствует адрес ячейки памяти).

В рассмотренном нами примере формальные параметры М и N являются параметрами-значениями. Это аргументы процедуры. При обращении к ней первый раз им соответствуют значения выражений а + b и abs (а - b); второй раз — с и а • b. Параметр K является параметром-переменной. В ней получается результат работы процедуры. В обоих обращениях к процедуре соответствующим фактическим параметром является переменная с. Через эту переменную основная программа получает результат.

Теперь рассмотрим другой вариант программы, решающей ту же задачу. В ней используется процедура без параметров.

Program NOD2;

Var A,B,K,M,N: Integer;

Procedure Evklid;

Begin

While M<>N Do

If M>N

Then M:=M-N

Else N:=N-M;

K:=M

End;

Begin

Write('a=');

ReadLn(A);

Write('b=');

ReadLn(B);

M:=A+B;

N:=Abs(A-B);

Evklid;

M:=K;

N:=A*B;

Evklid;

WriteLn('HOД равен',K)

End.

Чтобы разобраться в этом примере, требуется объяснить новое для нас понятие: область действия описания.

Областью действия описания любого программного объекта (переменной, типа, константы и т.д.) является тот блок, в котором расположено это описание .

Если данный блок вложен в другой (подпрограмма), то присутствующие в нем описания являются локальными. Они действуют только в пределах внутреннего блока. Описания же, стоящие во внешнем блоке, называются глобальными по отношению к внутреннему блоку. Если глобально описанный объект используется во внутреннем блоке, то на него распространяется внешнее (глобальное) описание.

В программе NOD1 переменные М, N, К — локальные внутри процедуры; переменные а, b, с — глобальные. Однако внутри процедуры переменные а, b, с не используются. Связь между внешним блоком и процедурой осуществляется через параметры.

В программе NOD2 все переменные являются глобальными. В процедуре Evklid нет ни одной локальной переменной (нет и параметров). Поэтому переменные М и N, используемые в процедуре, получают свои значения через оператор присваивания в основном блоке программы. Результат получается в глобальной переменной К, значение которой выводится на экран.

Использование механизма передачи через параметры делает процедуру более универсальной, независимой от основной программы. Однако в некоторых случаях оказывается удобнее использовать передачу через глобальные переменные. Чаще такое бывает с процедурами, работающими с большими объемами информации. В этой ситуации глобальное взаимодействие экономит память ЭВМ.

Функции. Теперь выясним, что такое подпрограмма-функция. Обычно функция используется в том случае, если результатом подпрограммы должна быть скалярная (простая) величина. Тип результата называется типом функции. В Турбо Паскале допускаются функции строкового типа. Синтаксическая диаграмма описания функции представлена на рис. 29.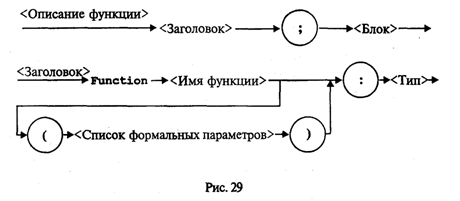



Как и у процедуры, у функции в списке формальных параметров могут присутствовать параметры-переменные и параметры-значения. Все это аргументы функции. Параметры вообще могут отсутствовать (если аргументы передаются глобально).

Программа решения рассмотренной выше задачи с использованием функции будет выглядеть следующим образом:

Program NOD3;

Var А,В,Rez:Integer;

Function Evklid(M,N:Integer):Integer;

Begin

While M<>N Do

If M>N

Then M:=M-N

Else N:=N-M;

Evklid:=M

End;

Begin

Write('a=');

ReadLn(A);

Write('b=');

ReadLn(B);

Rez:=Evklid(Evklid(A+B,Abs(A-B)),A*B);

WriteLn('NOD равен',Rez)

End.

Из примера видно, что тело функции отличается от тела процедуры только тем, что в функции результат присваивается переменной с тем же именем, что и функция.

Обращение к функции является операндом в выражении. Оно записывается в следующей форме:

<Имя функции> (<Список фактических параметров>)

Правила соответствия между формальными и фактическими параметрами все те же. Функция позволяет получить результат путем выполнения одного оператора присваивания. Здесь иллюстрируется возможность того, что фактическим аргументом при обращении к функции может быть эта же функция.

По правилам стандарта Паскаля возврат в вызывающую программу из подпрограммы происходит, когда выполнение подпрограммы доходит до ее конца (последний End). Однако в Турбо Паскале есть средство, позволяющее выйти из подпрограммы в любом ее месте. Это оператор-процедура Exit. Например, функцию определения наибольшего из двух данных вещественных чисел можно описать так:

Function Max(X,Y: Real): Real;

Begin

Max:=X;

If X>Y Then Exit Else Max:=Y

End;

Еще раз об области действия описаний. В Паскале неукоснительно действует следующее правило: любой программный объект (константа, переменная, тип и т.п.) должен быть описан перед использованием в программе. Иначе говоря, описание объекта должно предшествовать его первому появлению в других фрагментах программы. Это правило относится и к подпрограммам.

На рис. 30 схематически показана структура взаимного расположения описаний подпрограмм в некоторой условной программе. Попробуем, используя эту схему, разобраться в вопросе об области действия описаний подпрограмм.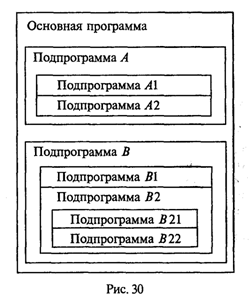



Любая подпрограмма может использоваться лишь в пределах области действия ее описания. Например, область действия подпрограмм А и В — основная программа. Поэтому из основной программы можно обратиться к подпрограммам А и В. В свою очередь, в подпрограмме В могут быть обращения к подпрограмме А; а из А нельзя обратиться к В, поскольку описание А предшествует описанию В. Подпрограммы А1 и А2 локализованы в подпрограмме A и могут использоваться только в ней; из А2 можно обратиться к A1, но не наоборот.

Из подпрограммы B1 можно обратиться к А, поскольку ее описание является глобальным по отношению к B1, но нельзя обратиться к А1, поскольку область действия описания А1 не распространяется на блок подпрограммы В.

Из подпрограммы В22 можнообратиться только к B21, B1, А.

Если одно и то же имя описано во внешнем блоке (глобально) и во внутреннем блоке (локально), то последнее описание (локальное) перекрывает первое в пределах внутреннего блока. Рассмотрим следующий пример:

Program Example1;               Program Example2;

Var X: Integer;                 Var X: Integer;

Procedure P;                    Procedure P;

Var X: Integer;                 Begin

Begin WriteLn('x=',X)               WriteLn('x=',X)

End;                            End;

Begin X:=1;                     Begin X:=l;

P                                     P

End.                            End.

Что выведется на экран в результате работы программы Example1 и Example2? Первая программа выдаст результат:

х=...

На месте многоточия будет какое-то произвольное значение, соответствующее неопределенной величине х. Вторая программа в результате даст

х=1

В первом случае переменная с именем х описана как глобально, так и локально. Но процедура выводит значение локальной переменной, которой ничего не присвоено. В этом примере идентификатором х обозначены две совершенно разные величины, им соответствуют две разные ячейки памяти.

Во втором примере переменная х одна на всю программу. Она описана глобально. Поэтому значение 1, присвоенное ей в основной программе, передается и в подпрограмму.

Далее разговор пойдет о ситуации на первый взгляд совершенно парадоксальной. Оказывается, подпрограмма в своем описании может содержать обращение к самой себе. Такая подпрограмма называется рекурсивной.

Рекурсивные подпрограммы. В математике рекурсивным называется определение любого понятия через самое себя. Классическим примером является определение факториала целого числа, большего или равного нулю: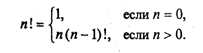



Здесь функция факториала определена через факториал. Нетрудно понять справедливость такого определения. Для п > 0



Вариант 0!=1 является тривиальным. Но это «опорное» значение, от которого начинается раскручивание всех последующих значений факториала:



Рассмотрим подпрограмму-функцию, использующую в своем описании приведенную выше рекурсивную формулу.

Function Factor(N: Pozint): Pozint;

Begin

If N=0

Then Factor:=1

Else Factor:=N*Factor(N-l)

End;

Предполагается, что тип PozInt объявлен глобально следующим образом:

Type PozInt=0..MaxInt;

Пусть в основной программе для вычисления в целой переменной х значения 3! используется оператор

X:=Factor(3);

При вычислении функции с аргументом 3 произойдет повторное обращение к функции Factor(2). Это обращение потребует вычисления Factor(1). И наконец, при вычислении Factor(0) будет получен числовой результат 1. Затем цепочка вычислений раскрутится в обратном порядке:

Factor(1)=l*Factor(0)=1

Factor(2)=2*Factor(1)=2

Factor(3)=3*Factor(2)=6.

Последовательность рекурсивных обращений к функции должна обязательно выходить на определенное значение. А весь маршрут последовательных вхождений машина запоминает в специальной области памяти, называемой стеком. Таким образом, выполнение рекурсивной функции происходит в два этапа: прямой ход — заполнение стека; обратный ход — цепочка вычислений по обратному маршруту, сохраненному в стеке.

Использование рекурсивных функций — красивый прием с точки зрения программистской эстетики. Однако этот путь не всегда самый рациональный. Рассмотренную задачу с п! можно решить так:

F:=l;

For I:=l To N Do

F:=F*I;

Очевидно, что такой вариант программы будет работать быстрее, чем рекурсивный. И в том случае, когда важнейшим является сокращение времени выполнения программы, следует отдать предпочтение последнему варианту.

В каждой конкретной реализации Паскаля имеется ограничение на количество рекурсивных обращений к подпрограмме (глубина рекурсии). Это связано с ограничением на размер стека. По этой причине можно попасть в ситуацию, когда рекурсивной подпрограммой вообще не удастся воспользоваться.

Рекурсивно определена может быть не только функция, но и процедура.