ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014. Учебное пособие для 1го курса оглавление Оглавление 2 основы программирования 2 Введение 2

• Название: Учебное пособие для 1го курса оглавление Оглавление 2 основы программирования 2 Введение 2
• Анкор: ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014.doc
• Дата: 20.04.2018
• Размер: 4.81 Mb.
• Имя файла: ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014.doc
• Тип: Учебное пособие; #18298
• страница: 15 из 17

3.17. Табличные данные и массивы

В повседневной и научной практике часто приходится встречаться с информацией, представленной в табличной форме. Вот, например, таблица, содержащая среднемесячные значения температуры, °С, за определенный год:



Такую таблицу называют линейной. Она представляет собой последовательность упорядоченных чисел. Если требуется какая-то математическая обработка этих данных, то для их обозначения обычно вводят индексную символику. Например, через Т1 обозначается температура января (первого месяца), Т5 — температура мая и т. д. В общем виде множество значений, содержащихся в таблице, обозначается так:

{Тi}, i=1,...,12.

Порядковые номера элементов (1, 5, i и т.д.) называются индексами. Индексированные величины удобно использовать для записи их математической обработки. Например, среднегодовая температура выражается следующей формулой:



Теперь представьте, что нам требуется собрать информацию о среднемесячных температурах за 10 лет, например с 1981 по 1990 г. Очевидно, что для этого удобна прямоугольная таблица, в которой столбцы соответствуют годам, а строки — месяцам.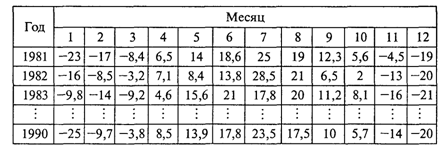



Обратите внимание на то, что уже сама удачно выбранная форма записи данных дает возможность достаточно удобно и быстро получить новую информацию. Например, из таблицы легко узнать, в каком году был самый холодный январь или какой месяц был самым нестабильным за десятилетие.

Для значений, хранящихся в такой таблице, удобно использовать двухиндексные обозначения. Например, H1981,2 обозначает температуру в феврале 1981 г. и т.п. А вся совокупность данных, составляющих таблицу, обозначается так:

{Hi,j}, i=1981. .1990; j=1..12

Обработка подобных данных производится с использованием двухиндексных величин. Например, средняя температура марта за 10 лет вычисляется по формуле:



А значение средней температуры за весь-десятилетний период вычисляется так:



В Паскале аналогом таблиц является структурированный тип данных, который называется регулярным типом, или массивом. Так же как и таблица, массив представляет собой совокупность пронумерованных однотипных значений, имеющих общее имя. Элементы массива обозначаются переменными с индексами. Индексы записывают в квадратных скобках после имени массива. Например:

T[1],T[5],T[i],H[1981,9],H[i,j] и т.п.

Массив, хранящий линейную таблицу, называется одномерным, прямоугольную таблицу — двумерным.

Тип элементов массива называется его базовым типом. Очевидно, что для рассмотренных массивов температур базовым типом является вещественный (Real).

Описание массивов. Переменная регулярного типа описывается в разделе описания переменных в следующей форме:

Var <идентификатор>: Array[<тип индекса>] Of <тип компонент>

Чаще всего в качестве типа индекса употребляется интервальный тип. Например, рассмотренный выше одномерный массив среднемесячных температур опишется так:

Var Т: Array[1..12] Of Real;

Описание массива определяет, во-первых, размещение массива в памяти, во-вторых, правила его дальнейшего употребления в программе. Последовательные элементы массива располагаются в последовательных ячейках памяти (T[1], T[2] и т. д.), причем значения индекса не должны выходить из диапазона 1... 12. В качестве индекса может употребляться любое выражение соответствующего типа. Например, Т[i+j], Т[m div 2].

Многомерный массив в Паскале трактуется как одномерный массив, тип элементов которого также является массивом (массив массивов). Например, рассмотренную выше прямоугольную таблицу можно хранить в массиве, описанном следующим образом:

Var H: Аггау[1981..1990]. Of Array[1..12] Of Real;

Вот примеры обозначения некоторых элементов этого массива:

Н[1981][1]; Н[1985][10]; Н[1990][12]

Однако чаще употребляется другая, эквивалентная форма обозначения элементов двумерного массива:

Н[1981,1]; Н[1985,10]; Н[1990,12]

Переменная H[1981] обозначает всю первую строку таблицы, т.е. весь массив температур за 1981 г.

Другим вариантом, эквивалентным приведенному выше описанию, является следующий:

Type    Month=Array[1..12] Of Real;

Year=Array [1981..1990] Of Month;

Var H: Year;

Наиболее краткий вариант описания данного массива такой:

Var H: Array[1981..1990,1..12] Of Real;

По аналогии с математикой одномерные числовые массивы часто называют векторами, а двумерные — матрицами.

В Паскале не допускается употребление динамических массивов, т.е. таких, размер которых определяется в процессе выполнения. Изменение размеров массива происходит через изменение в тексте программы и повторную компиляцию. Для упрощения таких изменений удобно определять индексные параметры в разделе констант:

Const Imax=10; Jmax=20;

Var Mas: Array[1..Imax,1..Jmax] Of Integer;

Теперь для изменения размеров массива Mas и всех операторов программы, связанных с этими размерами, достаточно отредактировать только одну строку в программе — раздел констант.

Действия над массивом как единым целым. Такие действия допустимы лишь в двух случаях:

• присваивание значений одного массива другому;

• операции отношения «равно», «не равно».

В обоих случаях массивы должны иметь одинаковые типы (тип индексов и тип элементов).

Следующий фрагмент программы организует построчный вывод матрицы на экран:

For I:=1 То IMax Do

Begin

For J:=l To JMax Do

Write(Mas[I,J]:6);

WriteLn

End;

После печати очередной строки матрицы оператор WriteLn без параметров переведет курсор в начало новой строки. Следует заметить, что в последнем примере матрица на экране будет получена в естественной форме прямоугольной таблицы, если JMax не превышает 12 (сами подумайте почему).

Рассмотрим несколько примеров типовых программ обработки массивов.

Пример 1. Вернемся к массиву среднемесячных температур T[1.. 12]. Требуется вычислить среднегодовую температуру, а также ежемесячные отклонения от этой величины.

Program Example;

Const N = 12;

Type Vec=Array [1..N] Of Real;

Var T,Dt: Vec;

St: Real;

I: Integer;

Begin (Ввод исходных данных)

WriteLn('Вводите таблицу температур');

For I:=l To N Do

Begin

Write(I: 2,':');

ReadLn(T[I])

End;

{Вычисление средней температуры}

St:=0;

For I:=1 To N Do

St:=St+T[I];

St:=St/N;

(Вычисление таблицы отклонений от среднего}

For I:=1 To N Do

Dt[I]:=T[I]-St;

{Вывод результатов}

WriteLn('Средняя температура равна',St:6:2);

WriteLn;

WriteLn('Отклонения от средней температуры:');

For I:=l To N Do

WriteLn(1:1,':',Dt[I]:6:2)

End.

По этой программе можно рассчитать среднее значение и вектор отклонений от среднего для любого одномерного вещественного массива. Настройка на размер массива осуществляется только редактированием раздела констант.

Пример 2. Выбор максимального элемента

Пусть из рассмотренного выше массива температур требуется отобрать самую высокую температуру и номер месяца, ей соответствующего. Идея алгоритма решения этой задачи: чтобы получить максимальную температуру в вещественной переменной TMах, сначала в нее заносится первое значение массива T[1]. Затем поочередно сравнивается значение TMах с остальными элементами массива температур, и каждое значение большее, чем TMах, присваивается этой переменной. Для получения номера самого теплого месяца в целой переменной NumMax в нее следует каждый раз засылать номер элемента массива температур одновременно с занесением в TMах его значения.

ТМах:=Т[1];

NumMax:=1;

For I:=2 To 12 Do

If T[I]>Tmax

Then

Begin

TMax:=T[I];

NumMax:=1

End;

Заметим, что если в массиве температур несколько значений, равных максимальному, то в NumMax будет получен первый номер из этих элементов. Чтобы получить последнюю дату, нужно в операторе If заменить знак отношения > на >=.

Пример 3. Сортировка массива. В одномерном массиве Х из N элементов требуется произвести перестановку значений так, чтобы они расположились по возрастанию, т.е. Х1 ≤ Х2 ≤... ≤ ХN.

Существует целый класс алгоритмов сортировки. Ниже описан алгоритм, который называется «метод пузырька».

Идея: производится последовательное упорядочивание смежных пар элементов массива: Х1 и X2, Х2 и Х3,.... ХN-1 и ХN. В итоге максимальное значение переместится в ХN. Затем ту же процедуру повторяют до XN-1 и т.д., вплоть до цепочки из двух элементов Х1 и X2. Такой алгоритм будет иметь структуру двух вложенных циклов с внутренним циклом — переменной (сокращающейся) длины.

For I:=1 То N-l Do

For K:=l To N-I Do

If Х[К]>Х [K+l]

Then

Begin

А:=Х[К];

Х[К]:=Х[К+1];

Х[К+1]:=А

End;