|
|
алгебра. Лекция № 1 от 11.04. Лекция 1 Матрицы и операции над ними Матрицей называется прямоугольная таблица чисел
11.04.2022 г.
Лекция № 1
Матрицы и операции над ними
Матрицей называется прямоугольная таблица чисел.
Числа, образующие матрицу называются элементами.
Матрицу обозначают заглавными латинскими буквами А, В, С,…, а их элементы – соответствующими малыми буквами с индексом, указывающим местоположение этого элемента в матрице.
Пусть матрица А состоит из 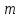 строк и строк и 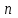 столбцов, тогда столбцов, тогда 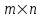 – размер матрицы, – размер матрицы, 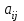 – элементы матрицы, i – номер строки (i = 1, 2,…., m), j – номер столбца (j = 1, 2,…, n). – элементы матрицы, i – номер строки (i = 1, 2,…., m), j – номер столбца (j = 1, 2,…, n).
В общем виде матрица записывается в виде:
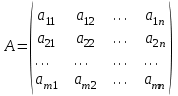
Количество строк и столбцов матрицы называется ее размерностью и обозначается dimA =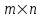 или в виде нижнего индекса: или в виде нижнего индекса: 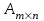
Элементы матрицы, у которых номер строки совпадает с номером столбца, образуют главную диагональ матрицы и называются диагональными элементами.
Если количество строк в матрице равно количеству ее столбцов, такая матрица называется квадратной. Для квадратной матрицы слово размерность обычно заменяют словом порядок: матрица n-го порядка имеет размерность 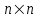 . .
Матрица, у которой все элементы не стоящие на главной диагонали, равны нулю, называется диагональной.
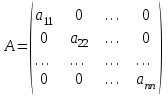
Квадратная матрица, у которой на главной диагонали находятся единицы, а все остальные элементы – нули, называется единичной.
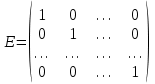
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Две матрицы называются равными тогда и только тогда, когда совпадают их размерности и каждый элемент первой матрицы равен соответствующему элементу второй матрицы.
Над матрицами, как и над любыми объектами математики можно производить некоторые операции.
1. Сложение матриц. Если размерности матриц А и В совпадают, то матрица С = А + В будет их суммой тогда и только тогда, когда имеет такую же размерность, как А и В, а каждый элемент матрицы С равен сумме соответствующих элементов матриц А и В.
Пример 1:
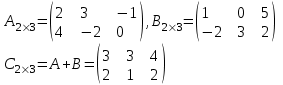
2. Умножение матрицы на число. Матрица С будет равна матрице А, умноженной на число λ тогда и только тогда, когда имеет такую же размерность, как А, а каждый элемент матрицы С равен произведению соответствующего элемента матрицы А и числа λ.
Пример 2: Дана матрица А. Найти С = 3·А.
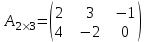
Решение:
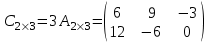
Свойства сложения матриц и умножения их на число:
1. А + В = В + А;
2. ( А + В) + С = А + (В + С);
3. α·(А + В) = α·А + α·В;
4. (α + β)·А = α·А + β·А;
5. α·(β·А) = (α·β)·А.
3. Транспонирование матриц. При транспонировании матрицы ее строки меняются местами со столбцами (первая строка становится первым столбцом и т.д.).
Операция над матрицей, при которой ее строки становятся столбцами с теми же номерами, а столбцы – строками, называется транспонированием и обозначается АТ.
Пример 3:Найти матрицу, транспонированной к матрице А.
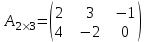
Решение:
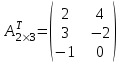
Операция транспонирования обладает следующими свойствами:
(А+В)Т = АТ + ВТ;
(αА)Т = αАТ;
(АТ)Т = А.
(А·В)Т = ВТ·АТ
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований и обозначается АВ.
Элементарные преобразования матриц:
1) перестановка местами двух строк матрицы (столбцов);
2) умножение всех элементов строки (столбца) матрицы на число, отличное от нуля;
3) прибавление ко всем элементам одно строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
4) вычеркивание нулевой строки (столбца) матрицы;
5) транспонирование матрицы.
С помощью элементарных преобразований матрицу можно привести к ступенчатому (треугольному) виду:
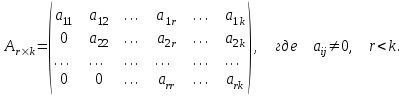
4. Произведение матриц. Две матрицы А и В называются согласованными, если число столбцов в первой матрице равно числу строк во второй.
Матрица С называется произведением согласованных матриц А и В, если она содержит столько же строк, сколько и матрица А и столько же столбцов, сколько матрица В, а элемент сij произведения равен сумме попарных произведений элементов i-той строки матрицы А на соответствующие элементы j-того столбца матрицы В:
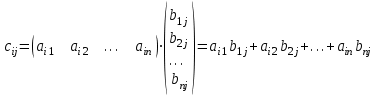
Пример 4:Даны матрицы А и В. Найти С = А·В и D = В·А.
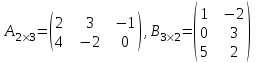
Решение: Найдем матрицу С.
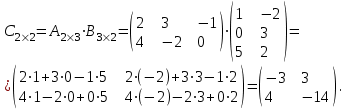
Найдем произведение матриц В и А:
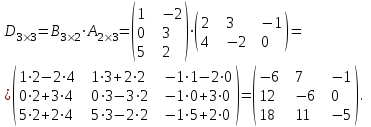
Этот пример доказывает, то А·В ≠ В·А.
Матрицы, для которых А·В = В·А, называются перестановочными. Очевидно, что для перестановочности необходимо (но не достаточно), чтобы А и В были квадратными матрицами одного порядка.
Свойства умножения матриц:
1. (А·В)·С = А·(В·С);
2. А·(α·В) = (α·А)·В = α·(А·В);
3. (А + В)·С = А·С + В·С;
4. С·(А + В) = С·А + С·В;
5. А·Е = Е·А = А, где Е – единичная матрица.
Степени матриц. Многочлены от матриц.
Целая неотрицательная степень матрицы определяется равенством:
Аn = А·А·А·….·А = Аn-1·А = А·Аn-1.
Пример 5: Найти значение многочлена f(A), если f(х) = х2 – 5х + 3 и
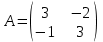
Решение: f(A) = A2 – 5A + 3E
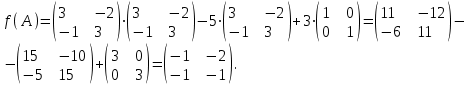
Определитель и его свойства
Для каждой квадратной матрицы А по определенному правилу можно вычислить число, называемое определителем этой матрицы.
Обозначается определитель n-ного порядка следующим образом:
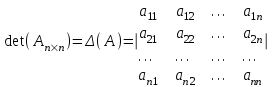
Определение определителя требует знание дополнительных понятий.
Минором Мijэлемента аij называется определитель, который получается из исходного определителя Δ(А) после вычеркивания i-той строки и j-того столбца, на пересечении которых стоит элемент аij.
Алгебраическим дополнением Аij элемента аij называется произведение соответствующего минора Мijна коэффициент (-1)i+j:
Аij= (-1)i+j·Мij.
Определитель n-ного порядка матрицы А равен сумме произведений элементов какой-либо строки или какого-либо столбца на алгебраические дополнения к этим элементам.
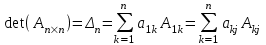
Определитель 1-го порядка:
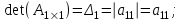
Определитель 2-го порядка при разложении по элементам первой строки:
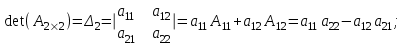
Определитель 3-го порядка при разложении по элементам первой строки:
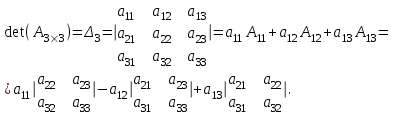
Пример 6: Вычислить определители
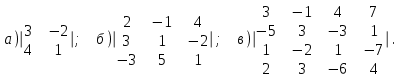
Решение:
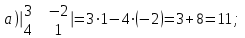
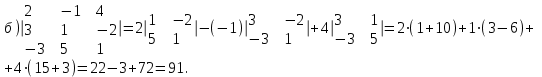
Мы вычислили определитель третьего порядка, раскладывая по элементам первой строки, но можно и по любому столбцу, например, по второму.
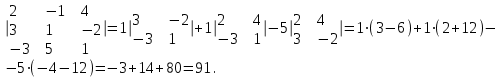
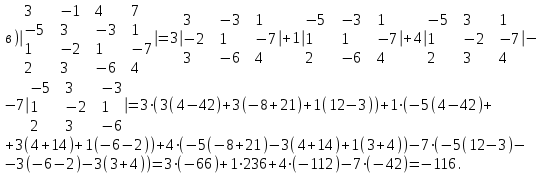
Одним из часто используемых методов вычисления определителя третьего порядка является вычисление по правилу Саррюса (или правила треугольников):
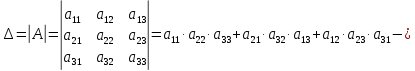
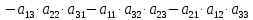
Запомнить эту формулу достаточно легко, если применить правило треугольников по схеме, по которой три произведения элементов в первом определителе берутся со знаком «+», а три других произведения элементов во втором определителе берутся со знаком «-».
              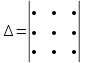 - -
Пример 6 (б):
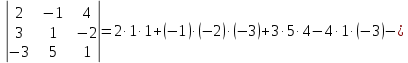
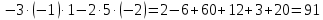
Свойства определителей
Строку или столбец определителя называют его рядом.
1. Определитель не изменится, если все строки определителя заменить столбцами, и наоборот (транспонировать определитель).
2.Если в определителе поменять местами двапараллельных ряда, то определитель изменит знак.
3. Если определитель содержит нулевую строку, то он равен нулю.
4. Если определитель содержит два одинаковых параллельных ряда, то он равен нулю.
5. Если определитель содержит пропорциональные параллельные ряды, то он равен нулю.
6. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
7. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель равен сумме двух определителей вида:
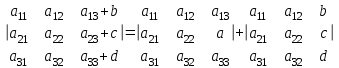
8. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число.
9. Сумма произведений всех элементов некоторого ряда определителя на алгебраические дополнения соответствующих элементов другого ряда равна нулю.
Пример 7: Вычислим определители из примера 6(б, в)по свойству 8.
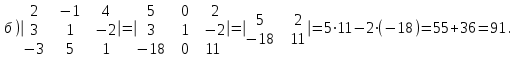
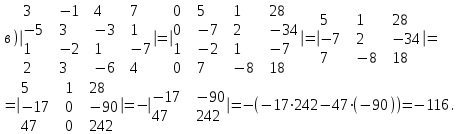
Обратная матрица
Матрица А-1 называется обратной к матрице А, если выполняется равенство: А·А-1 = А-1·А = E, где Е – единичная матрица того же порядка, что и матрица А.
Легко увидеть, что двойное равенство требует, чтобы матрицы А и А-1 были квадратными одного порядка. Однако, данное требование является необходимым, но не достаточным для существования обратной матрицы.
Квадратная матрица А называется невырожденной, если определитель данной матрицы не равен нулю: 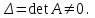
Теорема:Всякая невырожденная матрица имеет обратную.
Для любой невырожденной матрицы А существует единственная обратная матрица А-1, которую можно вычислить оп формуле: 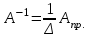 , где Апр. – матрица алгебраических дополнений. , где Апр. – матрица алгебраических дополнений.
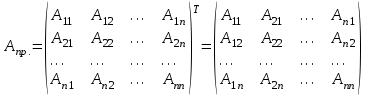 , Аij – алгебраические дополнения элемента аij. , Аij – алгебраические дополнения элемента аij.
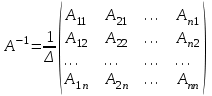
Свойства обратной матрицы
(А·В)-1 = В-1·А-1;
(А-1)-1 = А;
(АТ)-1 = (А-1)Т;
|А-1| = |А|-1 = 1/|А|.
Пример 8: Найти обратную матрицу.
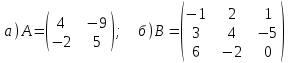
Решение:а) Вычислим определитель матрицы А.
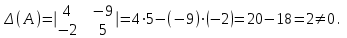
Найдем алгебраические дополнения:
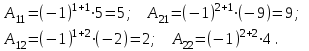
Тогда получаем А-1:
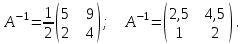
Проверка:
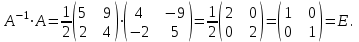
б) Вычислим определитель матрицы В.
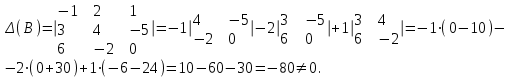
Найдем алгебраические дополнения:
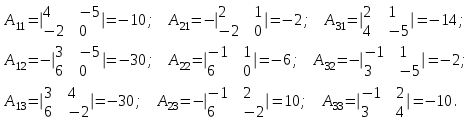
Тогда обратная матрица имеет вид:
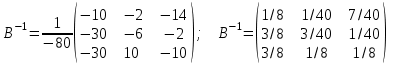
Сделаем проверку:
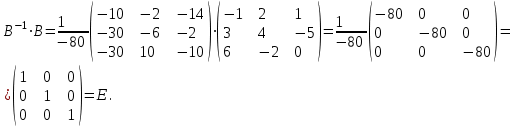
Обратная матрица связана с понятием деления и необходима тогда, когда требуется найти неизвестный множитель в матричном уравнении вида А·Х=В, где матрицы А и В известны, а матрицу Х необходимо найти. Очевидно, что задача однозначно решается только в случае, когда А квадратная и невырожденная, и следовательно существует А-1.Пусть А·Х = В и detА ≠ 0, тогда Х = А-1·В.
|
|
|
 Скачать 114.26 Kb.
Скачать 114.26 Kb.