Главная страница
Навигация по странице:

  • .

    		•

    банк заданий по теории вероятностей. Банк_задач_по_ТВ. печ. сб. окт.2010 (1). Учебное пособие для вузов Дружининская И. М. Хованская И. А. Матвеев В. Ф. Мышкис П. А


    Скачать 319.5 Kb.
    НазваниеУчебное пособие для вузов Дружининская И. М. Хованская И. А. Матвеев В. Ф. Мышкис П. А
    Анкорбанк заданий по теории вероятностей
    Дата08.05.2023
    Размер319.5 Kb.
    Формат файлаdoc
    Имя файлаБанк_задач_по_ТВ. печ. сб. окт.2010 (1).doc
    ТипУчебное пособие
    #1115239
    страница2 из 3
    1   2   3
    Часть вторая

    Простейшие задачи на
    непосредственное вычисление вероятности события,
    применение формул комбинаторики

    1. Игральная кость бросается два раза. Какова вероятность того, что оба раза выпадет одинаковое количество очков.

    2. Игральная кость бросается три раза. Найти вероятность того, что на верхней грани в первый раз выпадет пять очков, второй раз 6 очков, а третий раз два очка.

    3. В урне 4 белых и 3 черных шара. Из урны сразу вынимаются два шара. Найти вероятность того, что шары будут разных цветов.

    4. Какова вероятность, вытягивая из колоды в 36 карт 4 карты, вытянуть 2 дамы и два туза?

    5. На трех карточках помещены буквы «Г», «О», «Д». Карточки перемешаны и случайным образом подкладываются одна к другой. Какова вероятность, что получится слово «ГОД».

    6. На пяти карточках напечатана одна из следующих букв: п,о,р,т,с. Вынимая последовательно из ящика карточки наугад и выкладывая их в одну линию, можно получить слово «СПОРТ». Какова вероятность этого события?

    7. Пять человек случайным образом рассаживаются за круглым столом, среди них Оля и Петя. Найти вероятность того, что Оля и Петя будут сидеть рядом.

    Простейшие задачи на геометрическую вероятность

    1. В квадрат вписан равнобедренный треугольник так, что его основание совпадает со стороной квадрата. В квадрат случайным образом бросается точка. Найти вероятность того, что точка не попадет в треугольник.

    2. На плоскость нанесена система параллельных линий, расположенных на расстоянии 3 см друг от друга. На плоскость случайным образом брошена монета диаметром 1 см . Какова вероятность того, что монета не пересечет ни одну из линий?

    Простейшие задачи на применение основных свойств вероятностей

    1. Два охотника независимо друг от друга стреляют в одну и ту же утку. Вероятность попадания в утку одного из них равна 0.6, а другого 0.7. Найти вероятность попадания в утку.

    2. Событие А происходит с вероятность0.6. Событие Б происходит с вероятностью 0.7. Предполагается, что оба события независимы.
      Чему равна вероятность того, что произойдут оба события

    3. Событие А происходит с вероятность0.6. Событие Б происходит с вероятностью 0.7. Предполагается, что оба события независимы.
      Чему равна вероятность того, что произойдет только первое событие.

    4. Событие А происходит с вероятность0.6. Событие Б происходит с вероятностью 0.7. Предполагается, что оба события независимы.
      Чему равна вероятность того, что произойдет хотя бы одно событие.

    5. Событие А происходит с вероятность0.6. Событие Б происходит с вероятностью 0.7. Предполагается, что оба события независимы.
      Чему равна вероятность того, что события не произойдут.

    6. Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что потребитель увидит обе рекламы?

    7. Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что потребитель увидит хотя бы одну рекламу?

    8. Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что потребитель увидит только рекламу в каталоге?

    9. Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что потребитель не увидит рекламы этого товара?

    Простейшие задачи на основные распределения случайных величин.

    1. Производится серия независимых одинаковых испытаний. В каждом испытании вероятность появления события А одинакова и равна 0.7. Найти вероятность того, что в десяти испытаниях событие А возникнет три раза.

    2. Случайная величина имеет нормальное распределение с математическим ожиданием 1.7 и средним квадратическим отклонением 4. Какова вероятность попадания такой случайной величины в интервал (1; 2)? Показать математическое ожидание и полученную вероятность на графике плотности нормального распределения.

    3. Пусть . Найти вероятность попадания в промежуток . Построить график плотности заданного нормального распределения и указать на нем фигуру, соответствующую заданной вероятности.

    4. Случайная величина имеет равномерное распределение на отрезке
      [-3:4]. Найти вероятность попадания этой случайной величины в промежуток (-2; 2). Построить график плотности этого распределения и указать на нем фигуру, соответствующую вычисленной вероятности. Найти математическое ожидание и показать его на графике.

    5. Случайная величина имеет показательной распределение с параметром . Найти вероятность попадания этой случайной величины в промежуток (0; + ). Построить график плотности этого распределения и указать на нем фигуру, соответствующую найденной вероятности. Найти математическое ожидание и показать его на графике.

    6. Случайная величина подчинена закону распределения Пуассона, причем интенсивность потока событий равна 7 событий за единицу времени. Найти вероятность того, что за единицу времени произойдет ровно 5 событий.

    7. Имеется простейший поток событий, в котором время между двумя соседними событиями подчиняется экспоненциальному закону распределения. Найти вероятность того, что между двумя последовательными событиями пройдет менее 0.2 единиц времени, если интенсивность потока событий равна 7 событий за единицу времени.

    8. Случайная величина Х распределена по нормальному закону с параметрами m=10 и . Найти вероятность попадания Х в промежуток [6;12]. Построить график плотности заданного нормального распределения и указать на нем фигуру, соответствующую найденной вероятности.

    9. Случайная величина имеет равномерное распределение на интервале (5;7). Найти вероятность попадания Х в промежуток [5.5; 6]. Построить график плотности заданного равномерного распределения и указать на нем фигуру, соответствующую найденной вероятности. Вычислить математическое ожидание данной случайной величины и показать его на графике.

    10. Производится серия независимых испытаний. В каждом испытании вероятность появления события А одинакова и равна 0.4. Найти вероятность того, что в восьми испытаниях событие А возникнет шесть раз.

    11. Случайная величина имеет нормальное распределение с математическим ожиданием 3 и средним квадратическим отклонением 5. Какова вероятность попадания такой случайной величины в интервал (2; 9)? Показать математическое ожидание и вычисленную вероятность на графике плотности нормального распределения.

    12. Случайная величина подчинена закону распределения Пуассона, причем интенсивность потока событий равна 6.3 событий за единицу времени. Найти вероятность того, что за единицу времени произойдет ровно 5 событий.

    13. Имеется простейший поток событий, в котором время между двумя соседними событиями подчиняется экспоненциальному закону распределения. Найти вероятность того, что между двумя последовательными событиями пройдет не менее чем 0.1 единиц времени, если интенсивность потока событий равна 6.3 событий за единицу времени.

    Числовые характеристики случайных величин – математическое ожидание, дисперсия и среднее квадратическое отклонение

    1. Случайная величина имеет равномерное распределение на отрезке
      [0; 1]. Чему равны математическое ожидание и среднее квадратическое отклонение такой случайной величины?

    2. Случайная величина подчинена закону распределения Пуассона с интенсивностью потока событий, равному 3 событиям за час. Чему равны математическое ожидание и среднее квадратическое отклонение такой случайной величины?

    3. Случайная величина подчинена показательному (экспоненциальному) закону распределения с интенсивностью потока событий, равному 7 событий за год. Чему равны математическое ожидание и среднее квадратическое отклонение такой случайной величины?

    4. Непрерывная случайная величина подчинена закону распределения, плотность вероятности которого описывается формулой , если переменная x–величина положительная и плотность равна нулю, если переменная x – величина отрицательная. Чему равны математическое ожидание и среднее квадратическое отклонение такой случайной величины?

    5. Имеются две независимые случайные величины Х и Y с известными числовыми характеристиками: математические ожидания равны, соответственно, (-5) и 3, а дисперсии 4 и 9. Найти математическое ожидание и среднее квадратическое отклонение случайной величины Z=X-3Y.

    Часть третья

    Задачи на непосредственное вычисление вероятности события или
    применение формул комбинаторики

    1. На пяти карточках написаны буквы «П», «П», «О», «О», «Т». Найти вероятность того. Что при случайном выкладывании карточек друг за другом получится слово «ПОТОП».

    2. Среди кандидатов в студенческий совет факультета 4 первокурсника, 7 второкурсников и 7 третьекурсников. В совет наудачу выбирают 7 человек. Какова вероятность того, что будут выбраны одни третьекурсники?

    3. Среди кандидатов в студенческий совет факультета 4 первокурсника, 7 второкурсников и 7 третьекурсников. В совет наудачу выбирают 7 человек. Какова вероятность того, что будут выбраны 2 первокурсника и 3 третьекурсника?

    4. В ящике жетоны с номерами от 1 до 100. Какова вероятность, что первый вынутый жетон не содержит цифру 5?

    Задачи на геометрическую вероятность

    1. На плоскость с нанесенной сеткой квадратов со стороной 5см наудачу брошена монета радиуса 2см. Найти вероятность того, что монета не пересечет ни одной из сторон квадрата.

    2. Задача о встрече.
      Два друга договорились о встрече в стандартном для них месте "завтра где-то между 13 и 14 часами". Каждый из них прибыл на назначенное место в случайный момент времени из установленного интервала. Будучи "занятыми людьми", они не могли позволить себе ожидать другого более 10 минут. Однако считали за честь ожидать друга "максимально возможное время". Какова вероятность того, что встреча друзей состоялась?

    Задачи на применение основных свойств вероятностей

    1. Консультационная фирма претендует на два заказа от двух крупных корпораций А и Б. Эксперты фирмы считают, что вероятность получения консультационной работы в корпорации А равна 0.45. Эксперты также полагают, что если фирма получит заказ у корпорации А, то вероятность того, что и корпорация В обратится к ним, равна 0.9. Какова вероятность получения консультационной фирмой обоих заказов? (Ответ: 0.405)

    2. Менеджер разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в перовом, втором и третьем справочниках, соответственно равны 0.6, 0.7 и 0.8. Найти вероятность того, что формула содержится хотя бы в одном справочнике.

    3. Менеджер разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в перовом, втором и третьем справочниках, соответственно равны 0.6, 0.7 и 0.8. Найти вероятность того, что формула содержится в двух справочниках.

    4. Менеджер разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в перовом, втором и третьем справочниках, соответственно равны 0.6, 0.7 и 0.8. Найти вероятность того, что формула содержится во всех трех справочниках.

    5. Менеджер разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в перовом, втором и третьем справочниках, соответственно равны 0.6, 0.7 и 0.8. Найти вероятность того, что формула содержится только в первом и третьем справочниках

    6. Менеджер разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в перовом, втором и третьем справочниках, соответственно равны 0.6, 0.7 и 0.8. Найти вероятность того, что формула не содержится в двух справочниках.

    7. Вероятности попадания в цель при стрельбе для каждого из трех орудий равны: 0.8; 0.7; 0.9.Найти вероятность хотя бы одного попадания.

    8. В производственном цеху фирмы работают семь мужчин и три женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами. (Ответ: р=0.29).

    9. Преподаватель пригласил на собеседование трех из отстающих студентов через старосту группы. Староста забыл фамилии приглашенных и направил случайно трех из шести отстающих. Какова вероятность того, что это были нужные преподавателю студенты?

    10. Студент знает 10 вопросов из 25. Экзаменатор задал студенту 5 вопросов. Какова вероятность того, что студенту достались три вопроса из тех, которые он знает?

    11. В производственном цеху фирмы работают 6 мужчин и 4 женщины. В смену отобрали наугад 7 человек. Какова вероятность того, что среди них 3 женщины?

    12. Покупатель может приобрести акции трех компаний: А, В и С. В течение следующего года надежность первой компании оценивается экспертами в 99%, второй – в 98%, третьей - 97%. Чему равна вероятность того, что только одна компания в течение следующего года станет банкротом?

    13. Покупатель может приобрести акции трех компаний: А, В и С. В течение следующего года надежность первой компании оценивается экспертами в 99%, второй – в 98%, третьей - 97%. Чему равна вероятность того, что две компании обанкротятся?

    14. Покупатель может приобрести акции трех компаний: А, В и С. В течение следующего года надежность первой компании оценивается экспертами в 99%, второй – в 98%, третьей - 97%. Чему равна вероятность того, что все три компании станут банкротами?

    15. Покупатель может приобрести акции трех компаний: А, В и С. В течение следующего года надежность первой компании оценивается экспертами в 99%, второй – в 98%, третьей - 97%. Чему равна вероятность того, что наступит банкротство хотя бы одной компании?

    16. Покупатель может приобрести акции трех компаний: А, В и С. В течение следующего года надежность первой компании оценивается экспертами в 99%, второй – в 98%, третьей - 97%. Чему равна вероятность того, что обанкротится только компания А?

    17. Покупатель может приобрести акции трех компаний: А, В и С. В течение следующего года надежность первой компании оценивается экспертами в 99%, второй – в 98%, третьей - 97%. Чему равна вероятность того, что обанкротятся как компания А, так и компания С?

    18. Предприниматель решил вложить свои средства поровну в два "независимых" контракта, каждый из которых действует два года и принесет ему прибыль в размере 100%. Вероятность того, что каждый из контрактов за два года не «лопнет», равна 0.8. Какова вероятность риска? Или какова вероятность того, через два года по истечении срока действия этих контрактов, предприниматель, по меньшей мере, "ничего не потеряет"? (Ответ: 0.96).

    Формула полной вероятности и формула Байеса

    1. В данный район изделия поставляются тремя фирмами в отношении 3:4:6. Среди продукции первой фирмы стандартные изделия составляют 95%, второй – 80%, третьей – 75%. Найти вероятность того, что приобретенное изделие окажется нестандартным?

    2. В данный район изделия поставляются тремя фирмами в отношении 3:4:6. Среди продукции первой фирмы стандартные изделия составляют 95%, второй – 80%, третьей – 75%. Найти вероятность того, что приобретенной изделие оказалось стандартным?

    3. В данный район изделия поставляются тремя фирмами в отношении 3:4:6. Среди продукции первой фирмы стандартные изделия составляют 95%, второй – 80%, третьей – 75%. Найти вероятность того, что: а) приобретенное изделие окажется нестандартным; в) приобретенной изделие оказалось стандартным. Какова вероятность того, что оно изготовлено третьей фирмой?

    4. В данный район изделия поставляются тремя фирмами в отношении 3:4:6. Среди продукции первой фирмы стандартные изделия составляют 95%, второй – 80%, третьей – 75%. Приобретенное изделие оказалось нестандартным. Какова вероятность того, что оно изготовлено третьей фирмой?

    5. В данный район изделия поставляются тремя фирмами в отношении 3:4:6. Среди продукции первой фирмы стандартные изделия составляют 95%, второй – 80%, третьей – 75%. Приобретенное изделие оказалось стандартным. Какова вероятность того, что оно изготовлено второй фирмой?

    6. В первой коробке 20 радиоламп, из них стандартных 18; во второй 10, из них 9 стандартных. Из второй коробки переложили в первую одну наугад взятую лампу. Определить вероятность того, что затем наугад взятая лампа из первой коробки, является стандартной.

    7. Вероятность того, что деталь попадает первому контролеру, равна 0.6, а второму – 0.4. Вероятность того, что деталь признает стандартной первый контролер, равна 0.94, второй – 0.98. Найти вероятность того, что стандартную деталь проверил первый контролер.

    8. Три друга, студенты Щукинского училища, Иванов, Петров и Васечкин пошли в театр. В начале второго акта, возмущенные бездарной игрой одного из актеров, своего бывшего товарища, они одновременно достали из карманов специально заготовленные помидоры и бросили в него. При этом два помидора из трех попали в цель. Найти вероятность того, что Иванов попал в цель, если вероятности попадания в цель Ивановым, Петровым и Васечкиным, соответственно, равны 0.4, 0.3
      и 0.5. (Ответ: 20/29).

    9. Изделия были произведены с использованием двух технологических линий. На первой линии было произведено 2 изделия, на второй линии: 3 изделия. Вероятность того, что изделие будет отличного качества при производстве на первой линии равна 0.75, на второй – 0.7. Какова вероятность того, что случайно выбранной изделие будет отличного качества?

    10. Изделия были произведены с использованием двух технологических линий. На первой линии было произведено 2 изделия, на второй линии: 3 изделия. Вероятность того, что изделие будет отличного качества при производстве на первой линии равна 0.75, на второй – 0.7. Какова вероятность того, что случайно выбранной изделие отличного качества произведено на первой линии?

    11. На складе имеется 28 комплектующих изделий от двух компаний поставщиков, из них 20 изделий от первой компании. Известно, что с вероятностью 0.7 среди поставок первой компании встречаются изделия, выполненные по новейшей технологии. Среди изделий второй компании такие встречаются с вероятностью 0.8. Какова вероятность того, что случайным образом выбранное изделие выполнено по новейшей технологии?

    12. На складе имеется 28 комплектующих изделий от двух компаний поставщиков, из них 20 изделий от первой компании. Известно, что с вероятностью 0.7 среди поставок первой компании встречаются изделия, выполненные по новейшей технологии. Среди изделий второй компании такие встречаются с вероятностью 0.8. Случайным образом выбранное изделие оказалось выполненным по новейшей технологии. Какова вероятность того, что это изделие от первой компании?

    13. Имеются две группы студентов, состоящие из 20 и 25 человек. Свободно владеют английским языком 12 студентов из первой группы и 15 из второй группы. Какова вероятность того, что случайным образом выбранный из двух групп студент свободно владеет английским языком?

    14. Имеются две группы студентов, состоящие из 20 и 25 человек. Свободно владеют английским языком 12 студентов из первой группы и 15 из второй группы. Из двух групп случайным образом выбран один студент и оказалось, что он не владеет английским языком свободно. Какова вероятность того, что это студент первой группы?

    15. На склад поступили электроутюги, 80% с первого завода и 20% со второго. Среди продукции первого завода 90% выдерживают трехлетний гарантийный срок, со второго завода – 95%. Какова вероятность того, что взятый наугад со склада утюг выдержит трехлетний гарантийный срок? Какова вероятность того, что утюг с первого завода?

    16. На склад поступили электроутюги, 80% с первого завода и 20% со второго. Среди продукции первого завода 90% выдерживают трехлетний гарантийный срок, со второго завода – 95%. Какова вероятность того, что взятый наугад со склада утюг, выдерживающий трехлетний гарантийный срок, с первого завода?

    17. На сборку поступают однотипные изделия из двух цехов. Вероятности брака в каждом из них соответственно равны 0.04 и 0,03.Первый цех поставляет 30 изделий, второй 70. На сборку поступило бракованное изделие. Какова вероятность, что оно из второго цеха?

    18. В магазин бытовой техники поступила партия холодильников трех торговых марок: «Дед Мороз», «Снегурочка» и «Северный олень». В поступившей партии 10% холодильников «Дед Мороз», 40% холодильников «Снегурочка», остальные – «Северный олень». Известно, что холодильники данных торговых марок не требуют ремонта в течение гарантийного срока, соответственно, в 98%, 88% и 92% случаях. Найти вероятность того, что случайно выбранный из партии холодильник не потребует ремонта в течение гарантийного срока.

    19. В магазин бытовой техники поступила партия холодильников трех торговых марок: «Дед Мороз», «Снегурочка» и «Северный олень». В поступившей партии 10% холодильников «Дед Мороз», 40% холодильников «Снегурочка», остальные – «Северный олень». Известно, что холодильники данных торговых марок не требуют ремонта в течение гарантийного срока, соответственно, в 98%, 88% и 92% случаях. Случайно выбранный холодильник сломался в течение гарантийного срока. Какова вероятность того, что это холодильник марки «Снегурочка».

    20. Аналитик, занимающийся прогнозом котировок акций компании, ожидает роста стоимости акций с вероятностью 0.85, при условии, что экономика страны будет находиться в состоянии подъема. По его оценкам, в случае экономического спада, вероятность роста котировок акции компании снижается до 0.40. Согласно предварительным прогнозам вероятность экономического подъема в стране в следующем году оценивается на уровне 65%. Перед аналитиком поставлена задача: дать оценку вероятности роста цен на акции компании в новом году. Каков Ваш прогноз? (Ответ: р=0.693).

    21. Сотрудник консалтингового агентства проводит анализ тенденций на валютном рынке с целью расчета доходности будущих инвестиций. Согласно предварительному прогнозу, укрепление доллара США в период активного экономического роста ожидается с вероятностью 0.75; в период умеренного экономического роста с вероятностью 0.45 и в период стагнации с вероятностью 0.25. Кроме того, есть основания полагать, что активный экономический рост будет происходить с вероятностью 0.25, умеренный экономический рост с вероятностью 0.35 и будет наблюдаться стагнация с вероятностью 0.40.

    Какова вероятность того, что в прогнозируемый период произойдет укрепление доллара?

    1. Сотрудник консалтингового агентства проводит анализ тенденций на валютном рынке с целью расчета доходности будущих инвестиций. Согласно предварительному прогнозу, укрепление доллара США в период активного экономического роста ожидается с вероятностью 0.75; в период умеренного экономического роста с вероятностью 0.45 и в период стагнации с вероятностью 0.25. Кроме того, есть основания полагать, что активный экономический рост будет происходить с вероятностью 0.25, умеренный экономический рост с вероятностью 0.35 и будет наблюдаться стагнация с вероятностью 0.40.

    Известно, что в прогнозируемый период произошло укрепление доллара. Какова вероятность того, что этот период ознаменован высокими темпами экономического роста

    1. Имеется три партии ламп по 100, 200 и 300 штук. В первой партии 80% ламп с продолжительностью работы более 1 000 часов, во второй - 75%, в третьей – 60%. Какова вероятность того, что случайно выбранная из этих партий лампа проработает меньше 1 000 часов?

    2. Имеется три партии ламп по 100, 200 и 300 штук. В первой партии 80% ламп с продолжительностью работы более 1 000 часов, во второй - 75%, в третьей – 60%. Какова вероятность, что случайно выбранная лампа, проработавшая более 1000 часов, была взята из второй партии?

    Задачи на произвольные законы распределения и
    вычисление числовых характеристик для этих законов

    1. Распределение вероятностей случайной величины Х задается интегральной функцией распределения: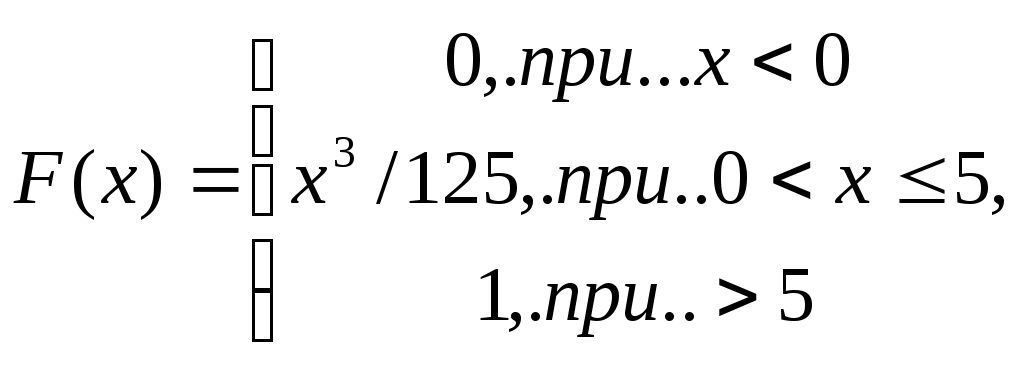



    Построить график функции плотности распределения вероятностей случайной величины Х. Вычислить вероятность попадания случайной величины в интервал (2;3). Найти для случайной величины Х математическое ожидание и среднее квадратическое отклонение. Показать вычисленную вероятность и математическое ожидание на графике функции плотности. (Ответы: р=0.152, ЕХ=3, = 0.968).

    1. Плотность распределения случайной величины Х имеет вид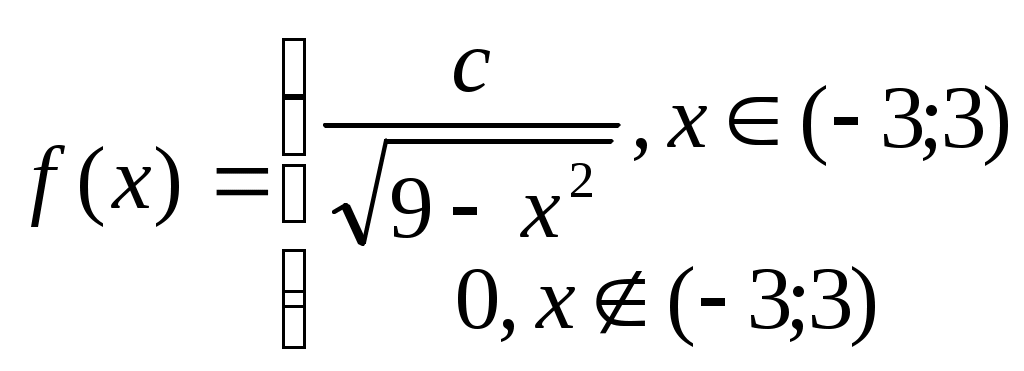



    Вычислить неизвестную константу с.
    Для случайной величины Х:
    а) Построить график функции плотности распределения вероятностей;
    б) Вычислить математическое ожидание и дисперсию.
    в) Найти вероятность попадания значений случайной величины Х в интервал (1;4).

    (Ответы: c=1/ ; ЕХ=0; DX=4.500; р=0.392).

    Задачи на биномиальное распределение
    (применение формулы Бернулли)

    1. Из 15 сбербанков 7 расположены за чертой города. Для обследования случайным образом отобрано 6 сбербанков. Какова вероятность того, что среди отобранных сбербанков только один окажется за чертой города?

    2. Фирма снабжает своей продукцией пять магазинов. От каждого магазина может поступить заявка на очередной день с вероятностью 0.4 независимо от заявок других магазинов.

    а) Какова вероятность того, что поступит не более двух заявок?

    б) Какова вероятность, что количество поступивших заявок будет лежать в пределах от двух до четырех?

    в) Найти наивероятнейшее число заявок в день и вероятность получения именно такого числа заявок?

    1. Известно, что 15% открывающихся малых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из пяти малых предприятий не более двух прекратят свою деятельность в течение года? Найти наивероятнейшее число малых предприятий, которые прекратят свою деятельность, и соответствующую этому вероятность.

    2. Мальчик Петя бросает камни в злобную соседскую собаку Рекса. Вероятность хотя бы одного попадания мальчика в собаку при трех бросках равна 0.875. Найти вероятность попадания в Рекса при одном броске, если вероятности попадания в собаку не меняются от броска к броску. (Ответ: р=0.5).

    Задачи на применение закона распределения Пуассона

    1. В страховую компанию в среднем поступает 2 иска в час. Определите вероятность того, что в течение 1,5 часов не поступит ни одного иска. Найти наивероятнейшее число поступивших за час исков и соответствующую этому вероятность.

    2. В книге из 200 страниц имеется 20 опечаток. Какова вероятность того. что на одной случайно выбранной странице имеется две опечатки. Найти наивероятнейшее число опечаток на одной странице и соответствующую этому вероятность.

    3. На АТС поступило 1000 звонков от абонентов. Вероятность неправильного соединения равна 0.005. Какова вероятность, что произошло 8 неправильных соединений? Найти наивероятнейшее число неправильных соединений и соответствующую этому вероятность.

    4. Из предшествующей работы фирмы известно, что при обзвоне 150 предприятий лишь 15 из них присылают своих представителей на фирму. Найти вероятность того, что при обзвоне 80 предприятий на фирму придут представители от 6 предприятий. Найти наивероятнейшее число приехавших представителей и соответствующую этому числу вероятность.

    Задачи на применение нормального закона распределения

    1. Месячная прибыль компании Мобильные телефоны Средиземья (МТС) является нормальной случайной величиной с математическим ожиданием 1 000 в валюте Средиземья и дисперсией 250 000. Чему равна вероятность того, что прибыль компании окажется:
      а) в пределах от 500 до 2 000?; б) более 1 250?
      Построить график плотности данного нормального распределения и указать на графике область, соответствующую вероятности из пункта а)

    2. Ежедневная прибыль супермаркета «На распутье» является нормальной случайной величиной с со средним значением 500 у.е. и неизвестной дисперсией. На основе наблюдений найдено, что вероятность отклонения от среднего значения в сторону уменьшения или увеличения ежедневной прибыли на 150 у.е. примерно равна 70%. Оценить величину среднего квадратического отклонения этой случайной величины и найти вероятность того, что в случайно выбранный день недели прибыль супермаркета превзойдет 700 у.е..

    3. Монета брошена 200 раз. Найти вероятность того, что герб выпадет ровно 80 раз. Найти вероятность того, герб выпадет более 150 раз. Найти наивероятнейшее число выпадений герба.

    4. При данном технологическом процессе 85% всей произведенной продукции является высшим сортом. Произведено 200 изделий. Какова вероятность того, что более 150 изделий будут изделиями высшего сорта? Найти наивероятнейшее число изделий высшего сорта.

    5. Имеется партия в 5000 деталей. Вероятность того, что деталь неисправна, равна 0.001. Найти вероятность того, что в этой партии 10 деталей неисправны. Найти наивероятнейшее число неисправных деталей в этой партии и соответствующую этому числу вероятность.

    6. Процент всхожести семян 90%. Оценить вероятность того, что из тысячи посеянных семян взойдет от 850 до 950 включительно. Найти наивероятнейшее число всхожести семян.

    7. Произведено 600 изделий. Вероятность брака для одного изделия
      равна 0.2. Найти вероятность того, что количество бракованных изделий превзойдет 400. Найти наивероятнейшее число бракованных изделий.

    8. Имеется партия в 1800 деталей. Вероятность того, что деталь окажется бракованной, равна 0.02. а) Найти вероятность того, что в этой партии 30 деталей неисправны. б) Найти вероятность того, что количество неисправных деталей будет менее 30. в) Найти вероятность того, что количество неисправных деталей будет от 30 до 50. г) Найти наивероятнейшее число неисправных деталей и соответствующую этому вероятность.

    9. Вероятность того, что компакт-диски, подготовленные для записи информации, имеют дефекты, равна 0.02. Для записи взяты 1200 дисков. Какова вероятность того, что: а) менее 15 дисков будут бракованными;
      б) ровно 20 дисков будут иметь брак?

    10. Из винтовки произведено 900 выстрелов. Вероятность попадания в мишень при одном выстреле равна 0.7. Найти вероятность того, что произойдет ровно 555 попаданий. Найти вероятность того, что произойдет менее 800 попаданий. Найти наивероятнейшее число попаданий.

    Задачи на показательный закон распределения

    1. Замечено, что посетители офиса данной фирмы образуют пуассоновский поток. Подсчитано, что в среднем приходят 4 человека в час. Найти вероятность того, что: а) за час никто не придет, б) в течение получаса придут 3 человека; в) за 45 минут придут более двух человек.

    2. В банке оператор тратит на обслуживание одного клиента в среднем 20 минут. Какова вероятность того, что: а) за один час оператор обслужит два клиента; б) менее двух клиентов?

    3. Случайная величина имеет показательной распределение с параметром . Найти вероятность попадания этой случайной величины в промежуток (-1.5; 3.2). Построить график плотности этого распределения и указать на нем фигуру, соответствующую найденной вероятности. Найти математическое ожидание и показать его на графике. Найти дисперсию и среднее квадратическое отклонение этой случайной величины.

    4. Непрерывная случайная величина имеет плотность распределения следующего вида: . Найти неизвестный параметр распределения. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение. Показать на графике плотности значения математического ожидания и среднего квадратического отклонения. Найти вероятность попадания значений случайной величины в интервал ; показать на графике эту вероятность.

    5. Получить ряд распределения для случайной величины – числа попаданий в цель при двух выстрелах, если вероятность попадания в цель равна 0.8 при одном выстреле. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины. Построить график функции распределения и показать на нем математическое ожидание и среднее квадратическое отклонение.

    Числовые характеристики случайных величин и их свойства

    1. Имеются две независимых случайных величины и с известными математическим ожиданием и дисперсией:

    Найти математическое ожидание и дисперсию случайной величины .

    1. Коэффициент корреляции между случайными величинами и равен . Найдите коэффициент корреляции между случайными величинами и .

    2. Имеются три независимые случайные величины X, Y, Z с известными математическими ожиданиями, которые, соответственно, равны (-5), (-2) и 3. Найти математические ожидания двух других случайных величин и .

    3. Доход фирмы за месяц представляется нормально распределенной случайной величиной со средним значением 3 млн. долл. и средним квадратическим отклонением 0.5 млн. долл. . Найдите вероятность того, что в данном месяце доход фирмы будет более 4 млн. долл. Напишите формулу плотности распределения этой случайной величины, нарисуйте ее график и покажите на нем вычисленную вероятность.

    4. Доход фирмы за месяц представляется нормально распределенной случайной величиной со средним квадратическим отклонением 0.5 млн. долл. Известно, что в 70% случаев доход фирмы превышает 4 млн. долл. Найдите средний доход фирмы.

    5. Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного более чем на 20 секунд.

    Зависимые и независимые случайные величины

    1. Сотрудник фирмы, отвечающий на телефонные звонки, получает много обращений по разным вопросам. В 75% случаев лишь запрашивается информация, в то время как 15% звонков связаны с реальными заказами. Кроме того, в 10% случаев запрашивается информация и делается заказ.
      а) Являются ли события – «запрашивается информация» и «делается заказ» – зависимыми? б) Найдите условную вероятность того, что некоторый звонок не связан с обращением за информацией при условии, что в результате звонка делается заказ.

    1   2   3

    написать администратору сайта