Учебное пособие Курск 2016
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
Формы адекватности информации. В процессе обработки информация может менять структуру и форму. Признаком структуры являются элементы информации и их взаимосвязь. Формы представления информации могут быть различны. Основными из них являются: символьная (основана на использовании различных символов), текстовая (текст — это символы, расположенные в определенном порядке), графическая (различные виды изображений), звуковая. Одной из важнейших характеристик информации является ее адекватность. Каждой форме адекватности соответствует своя мера количества информации. В повседневной практике такие понятия, как информация и данные, часто рассматриваются как синонимы. На самом деле между ними имеются различия. Данными называется информация, представленная в удобном для обработки виде. Данные могут быть представлены в виде текста, графики, аудиовизуального ряда. Представление данных называется языком информатики, представляющим собой совокупность символов, соглашений и правил, используемых для общения, отображения, передачи информации в электронном виде. Адекватность информации — это уровень соответствия образа, создаваемого с помощью информации, реальному объекту, процессу, явлению. От степени адекватности информации зависит правильность принятия решения. Адекватность информации может выражаться в трех формах: синтаксической, семантической и прагматической. Синтаксическая адекватность отображает формально-структурные характеристики информации, не затрагивая ее смыслового содержания. На синтаксическом уровне учитываются тип носителя и способ представления информации, скорость ее передачи и обработки, размеры кодов представления информации, надежность и Точность преобразования этих кодов и т. д. Информацию, рассматриваемую с таких позиций, обычно называют данными. Семантическая адекватность определяет степень соответствия образа объекта самому объекту. Здесь учитывается смысловое содержание информации. На этом уровне анализируются сведения, отражаемые информацией, рассматриваются смысловые связи. Таким образом, семантическая адекватность проявляется при наличии единства информации и пользователя. Эта форма служит для формирования понятий и представлений, выявления смысла, содержания информации и ее обобщения. Прагматическая адекватность отражает соответствие информации цели управления, реализуемой на ее основе. Прагматические свойства информации проявляются при наличии единства информации, пользователя и цели управления. На этом уровне анализируются потребительские свойства информации, связанные с практическим использованием информации, с соответствием ее целевой функции деятельности системы. Синтаксическая мера информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту. На этом уровне объем данных в сообщении измеряется количеством символов в этом сообщении. В современных ЭВМ минимальной единицей измерения данных является бит — один двоичный разряд. Широко используются также более крупные единицы измерения: байт, равный 8 битам; килобайт, равный 1024 байтам; мегабайт, равный 1024 килобайтам, и т. д. Семантическая мера информации используется для измерения смыслового содержания информации. Наибольшее распространение здесь получила тезаурусная мера, связывающая семантические свойства информации со способностью пользователя принимать поступившее сообщение. Тезаурус — это совокупность сведений, которыми располагает пользователь или система. Максимальное количество семантической информации потребитель получает при согласовании ее смыслового содержания со своим тезаурусом, когда поступающая информация понятна пользователю и несет ему ранее не известные сведения. С семантической мерой количества информации связан коэффициент содержательности, определяемый как отношение количества семантической информации к общему объему данных. Прагматическая мера информации определяет ее полезность, ценность для процесса управления. Обычно ценность информации измеряется в тех же единицах, что и целевая функция управления системой. Классификация мер. Для измерения информации вводятся два параметра: количество информации I и объем данных Vд. Эти параметры имеют разные выражения и интерпретацию в зависимости от рассматриваемой формы адекватности. Каждой форме адекватности соответствует своя мера количества информации и объема данных Синтаксическая мера информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту. Объем данных Vд в сообщении измеряется количеством символов (разрядов) в этом сообщении. В различных системах счисления один разряд имеет различный вес и соответственно меняется единица измерения данных: • в двоичной системе счисления единица измерения – бит (bit – binary digit – двоичный разряд). В современных ЭВМ наряду с минимальной единицей измерения данных «бит» широко используется укрупненные единицы измерения байт – 23 бит, слово – 24 бит, двойное слово 25 бит, килобайт – 210 байт; мегабайт – 210 килобайт, гигабайт – 210 мегабайт; • в десятичной системе счисления единица измерения – дит (десятичный разряд). Пример 1. Сообщение в двоичной системе в виде восьмиразрядного двоичного кода 10111011 имеет объем данных Vд = 8 бит. Сообщение в десятичной системе в виде шестиразрядного числа 275903 имеет объем данных Vд= 6 дит. Количество информации I на синтаксическом уровне определяется в связи с понятием неопределенности состояния системы (энтропии системы). Считается что получение информации о какой-либо системе всегда связано с изменением степени неосведомленности получателя о состоянии этой системы. Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе α. Мерой его неосведомленности о системе является функция H(α), которая в то же время служит и мерой неопределенности состояния системы. После получения некоторого сообщения β получатель приобрел некоторую дополнительную информацию Iβ(α), уменьшившую его априорную неосведомленность так, что неопределенность состояния системы после получения сообщения β стала Hβ(α). Тогда количество информации Iβ(α) ξ системе, полученной в сообщении β, определится как Iβ(α)=H(α)-Hβ(α). т.е. количество информации измеряется изменением (уменьшением) неопределенности состояния системы. Если конечная неопределенность Hβ(α) ξбратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации Iβ(α)=H(α). Иными словами, энтропия системы Н(а) может рассматриваться как мера недостающей информации. Энтропия системы H(α), θмеющая N возможных состояний, согласно формуле Шеннона, равна: 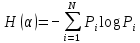 , где Pi — вероятность того, что система находится в i-м состоянии. Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны , где Pi — вероятность того, что система находится в i-м состоянии. Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны 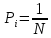 , ее энтропия определяется соотношением , ее энтропия определяется соотношением 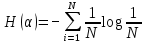 . . Наиболее часто используются двоичные и десятичные логарифмы. Единицами измерения в этих случаях будут соответственно бит и дит. Коэффициент (степень) информативности (лаконичность) сообщения определяется отношением количества информации к объему данных, т.е., причем 0 С увеличением Y уменьшаются работы по преобразованию информации (данных) в системе. Поэтому стремятся к повышению информативности, для чего разрабатываются специальные методы оптимального кодирования информации. Семантическая мера информации. Для измерения смыслового содержания информации, т.е. ее количества на семантическом уровне, наибольшее признание получила тезаурусная мера, которая связывает семантические свойства информации со способностью пользователя принимать поступившее сообщение. Для этого используется понятие тезаурус пользователя. Тезаурус - это совокупность сведений, которыми располагает пользователь или система. В зависимости от соотношений между смысловым содержанием информации S и тезаурусом пользователя Sp изменяется количество семантической информации Ic воспринимаемой пользователем и включаемой им в дальнейшем в свой тезаурус. Максимальное количество семантической информации Ic потребитель приобретает при согласовании ее смыслового содержания S со своим тезаурусом Sp, когда поступающая информация понятна пользователю и несет ему ранее не известные (отсутствующие в его тезаурусе) сведения. Следовательно, количество семантической информации в сообщении, количество новых знаний, получаемых пользователем, является величиной относительной. Одно и то же сообщение может иметь смысловое содержание для компетентного пользователя и быть бессмысленным (семантический шум) для пользователя некомпетентного. Относительной мерой количества семантической информации может служить коэффициент содержательности C, который определяется как отношение количества семантической информации к ее объему: Прагматическая мера информации. Эта мера определяет полезность информации (ценность) для достижения пользователем поставленной цели. Эта мера также величина относительная, обусловленная особенностями использования этой информации в той или иной системе. Ценность информации целесообразно измерять в тех же самых единицах (или близких к ним), в которых измеряется целевая функция. Для сопоставления введенные меры информации представим в таб. 1
Таблица 1. Единицы измерения информации Понятие системы счисления, виды систем счисления На ранних ступенях развития общества люди почти не умели считать. Они отличали друг от друга совокупности двух и трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятии «много». Это был еще не счет, а лишь его зародыш. Впоследствии способность различать друг от друга небольшие совокупности развивалась; возникли слова для обозначений понятий «четыре», «пять», «шесть», «семь». С усложнением хозяйственной деятельности людей понадобилось вести счет в более обширных пределах. Для этого человек пользовался окружавшими его предметами, как инструментами счета: он делал зарубки на палках и на деревьях, завязывал узлы на веревках, складывал камешки в кучки и т.п. Такой вид счета носит название унарной системы счисления, т.е. система счисления, в которой для записи числа применяется только один вид знаков. Это удобно, так как сразу визуально определяется количество знаков и сопоставляется с количеством предметов, которые эти знаки обозначают Особо важную роль играл природный инструмент человека – его пальцы. Этот инструмент не мог длительно хранить результат счета, но зато всегда был «под рукой» и отличался большой подвижностью. Поэтому, вполне естественно, что вновь возникавшие названия «больших» чисел часто строились на основе числа 10 – по количеству пальцев на руках; у некоторых народов возникали также названия чисел на основе числа 5 – по количеству пальцев на одной руке или на основе числа 20 – по количеству пальцев на руках и ногах. На современном этапе границы счета определены термином «бесконечность», который не обозначает какое либо конкретное число. Десятичная система счисления В современном русском языке, а также в языках других народов названия всех чисел до миллиона составляются из 37 слов, обозначающих числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 , 12, 13, 14, 15, 16, 17, 18, 19, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000 (например, восемьсот пятнадцать тысяч триста девяносто четыре). В свою очередь названия этих 37 чисел, как правило, образованы из названий чисел первого десятка (1, 2, 3, 4, 5, 6, 7, 8, 9) и чисел 10, 100, 1000 (например, 18 = восемь на десять, 30 = тридесять и т.д.). В основе этого словообразования лежит число десять, и поэтому наша система наименований называется десятичной системой счисления. Древнегреческая нумерация В древнейшее время в Греции была распространена т.н. аттическая нумерация. Числа 1, 2, 3, 4 обозначались черточками  , , 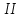 , ,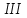 , ,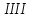 . Число 5 записывалось знаком . Число 5 записывалось знаком  (древнее начертание буквы «пи», с которой начинается слово «пенте» – пять); числа 6, 7, 8, 9 обозначались (древнее начертание буквы «пи», с которой начинается слово «пенте» – пять); числа 6, 7, 8, 9 обозначались 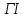 , , 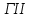 , , 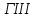 , , 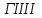 . Число 10 обозначалось . Число 10 обозначалось 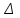 (начальной буквой слова «дека» – десять). Числа 100, 1000 и 10000 обозначались (начальной буквой слова «дека» – десять). Числа 100, 1000 и 10000 обозначались  , , 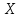 , , 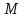 . Числа 50, 500, 5000 обозначались комбинациями знаков 5 и 10, 5 и 100, 5 и 1000. Общую запись чисел в аттической нумерации иллюстрирует пример 2. . Числа 50, 500, 5000 обозначались комбинациями знаков 5 и 10, 5 и 100, 5 и 1000. Общую запись чисел в аттической нумерации иллюстрирует пример 2.В третьем веке до н.э. аттическая нумерация была вытеснена так называемой ионийской системой. В ней числа 1 – 9 обозначались первыми девятью буквами алфавита; числа 10, 20, 30, … , 90 – следующими девятью буквами; числа 100, 200, … , 900 – последними девятью буквами. Таблица 2 Обозначение чисел в ионийской системе нумерации
Пример 2. Запись чисел в аттической системе счисления
Пример 3 Запись чисел в ионийской системе счисления
Такую же алфавитную нумерацию имели в древности евреи, арабы и многие другие народы Ближнего Востока. Славянская нумерация Южные и восточные славянские народы для записи чисел пользовались алфавитной нумерацией. У одних славянских народов числовые значения букв установились в порядке славянского алфавита, у других же (в том числе у русских) роль цифр играли не все буквы, а только те, которые имеются в греческом алфавите. Над буквой, обозначавшей цифру, ставился специальный значок: 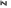 («титло»). («титло»).В России славянская нумерация сохранилась до конца XVII века. При Петре I возобладала так называемая «арабская нумерация», которой мы пользуемся и сейчас. Славянская нумерация сохранялась только в богослужебных книгах. В таблице 3 приведены славянские цифры. При записи чисел, больших 10, цифры писались слева направо в порядке убывания десятичных разрядов (однако иногда для чисел от 11 до 19 единицы записывались ранее десяти). Для обозначения тысяч перед числом их (слева внизу) ставился особый знак  . .Пример 4 иллюстрирует написание чисел в славянской системе нумерации. Таблица 3 Обозначение чисел в древнеславянской системе нумерации
Пример 4 Запись чисел в древнеславянской системе счисления
Пример 5 Запись чисел римскими цифрами
Римская нумерация Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени под именем «римской нумерации». Мы пользуемся ей для обозначения веков, юбилейных дат, наименования съездов и конференций, для нумерации глав книги или строф стихотворения. В позднейшем своем виде римские цифры выглядят так: 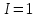 , , 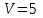 , ,  , , 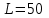 , ,  , , 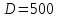 , , 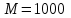 . .В римской нумерации явственно сказываются следы пятиричной системы счисления. В языке же римлян (латинском) никаких следов пятиричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (предположительно у этрусков). Все целые числа (до 5000) записываются с помощью повторения вышеприведенных цифр. При этом, если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае она не может повторяться), то меньшая вычитается из большей. Подряд одна и та же цифра ставится не более трех раз. Основные понятия и определения Выше мы говорили о системах счисления, не вдаваясь в подробности этого понятия. Каково же научное определение системы счисления? Системой счисления называют систему приемов и правил, позволяющих устанавливать взаимно-однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов. Множество символов, используемых для такого представления, называют цифрами. В зависимости от способа изображения чисел с помощью цифр системы счисления делятся на позиционные и непозиционные. В непозиционных системах любое число определяется как некоторая функция от численных значений совокупности цифр, представляющих это число. Цифры в непозиционных системах счисления соответствуют некоторым фиксированным числам. Пример непозиционной системы – рассмотренная ранее римская система счисления. Дpевние египтяне пpименяли систему счисления, состоящую из набоpа символов, изобpажавших pаспpостpаненные пpедметы быта. Совокупность этих символов обозначала число. Расположение их в числе не имело значения, отсюда и появилось название. Исторически первыми системами счисления были именно непозиционные системы. Одним из основных недостатков является трудность записи больших чисел. Запись больших чисел в таких системах либо очень громоздка, либо алфавит системы чрезвычайно велик. В вычислительной технике непозиционные системы не применяются. Систему счисления называют позиционной, если одна и та же цифра может принимать различные численные значения в зависимости от номера разряда этой цифры в совокупности цифр, представляющих заданное число. Пример такой системы – арабская десятичная система счисления. Количества и количественные составляющие, существующие реально могут отображаться различными способами. В общем случае в позиционной системе счисления число N может быть представлено как: 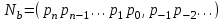 , , 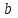 – основание системы счисления (целое положительное число, равное числу цифр в данной системе); – основание системы счисления (целое положительное число, равное числу цифр в данной системе);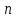 – любые цифры из интервала от нуля до – любые цифры из интервала от нуля до 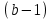 . .Основание позиционной системы счисления определяет ее название. В вычислительной технике применяются двоичная, восьмеричная, десятичная и шестнадцатеричная системы. В дальнейшем, чтобы явно указать используемую систему счисления, будем заключать число в скобки и в нижнем индексе указывать основание системы счисления. Каждой позиции в числе соответствует позиционный (разрядный) коэффициент или вес. Покажем это на примере десятичного числа: Пример 4, Способ образования десятичного числа 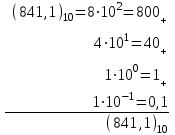 Для десятичной системы соответствия между позицией и весом следующее: 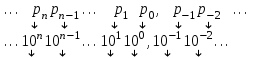 (1) (1)в общем случае: 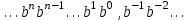 (2) (2)В настоящее время позиционные системы счисления более широко распространены, чем непозиционные. Это объясняется тем, что они позволяют записывать большие числа с помощью сравнительно небольшого числа знаков. Еще более важное преимущество позиционных систем - это простота и легкость выполнения арифметических операций над числами, записанными в этих системах. Вычислительные машины в принципе могут быть построены в любой системе счисления. Но столь привычная для нас десятичная система окажется крайне неудобной. Если в механических вычислительных устройствах, использующих десятичную систему, достаточно просто применить элемент со множеством состояний (колесо с десятью зубьями), то в электронных машинах надо было бы иметь 10 различных потенциалов в цепях. Наиболее удобной для построения ЭВМ оказалась двоичная система счисления, т.е. система счисления, в которой используются только две цифры: 0 и 1, т.к. с технической точки зрения создать устройство с двумя состояниями проще, также упрощается различение этих состояний. Для представления этих состояний в цифровых системах достаточно иметь электронные схемы, которые могут принимать два состояния, четко различающиеся значением какой-либо электрической величины – потенциала или тока. Одному из значений этой величины соответствует цифра 0, другому – 1. Относительная простота создания электронных схем с двумя электрическими состояниями и привела к тому, что двоичное представление чисел доминирует в современной цифровой технике. При этом 0 обычно представляется низким уровнем потенциала, а 1 – высоким уровнем. Такой способ представления называется положительной логикой. Перевод чисел из одной системы счисления в другую Системы счисления, используемые в компьютерах. Таблица 4.Таблица соответствия систем счисления.
|

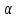
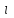
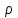
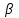
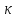
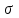
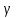
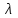
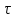
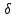
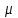
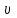
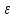
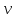
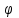
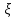
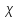
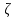
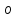
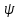
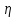

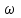
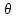
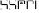
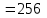 ,
,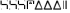
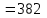 ,
,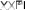
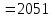 ,
,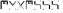
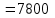 .
.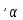
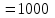 ,
,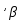
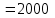 ,
,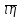
 ,
,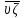
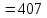 ,
,
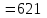 .
.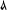





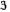
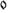
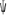
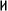
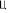
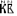
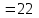 ,
,
 ,
,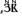
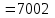 ,
,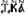
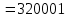 .
.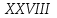
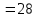 ,
,
 ,
,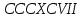
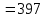 ,
,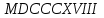
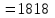 .
.