Учебное пособие Курск 2016
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
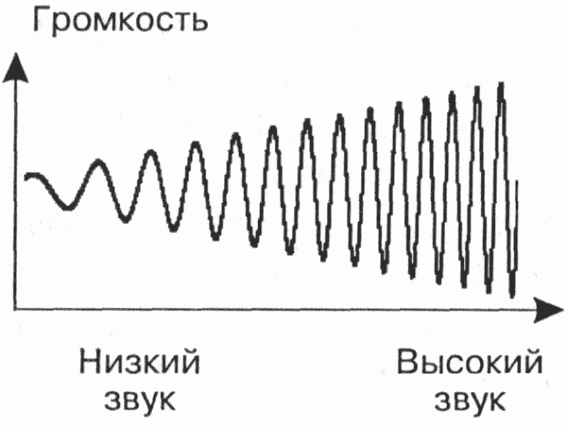
Задача 1. Шарик находится в одной из трех урн: А, В или С. Определить сколько бит информации содержит сообщение о том, что он находится в урне В. Решение. Такое сообщение содержит I = log2 3 = 1,585 бита информации. Приведем другие примеры равновероятных сообщений: При бросании монеты: "выпала решка", "выпал орел"; На странице книги: "количество букв чётное", "количество букв нечётное". Определим теперь, являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины. В 1948 г. американский инженер и математик К Шеннон предложил формулу для вычисления количества информации для событий с различными вероятностями. Если I - количество информации, К - количество возможных событий, рi - вероятности отдельных событий, то количество информации для событий с различными вероятностями можно определить по формуле: 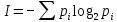 , где i принимает значения от 1 до К. , где i принимает значения от 1 до К.Формулу Хартли теперь можно рассматривать как частный случай формулы Шеннона: 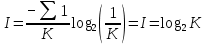 При равновероятных событиях получаемое количество информации максимально. Задача 2. Определить количество информации, получаемое при реализации одного из событий, если бросают несимметричную четырехгранную пирамидку; симметричную и однородную четырехгранную пирамидку. Решение. Будем бросать несимметричную четырехгранную пирамидку. Вероятность отдельных событий будет такова: р1 = 1 / 2, р2 = 1 / 4, р3 = 1 / 8, р4 = 1 / 8, тогда количество информации, получаемой после реализации одного из этих событий, рассчитывается по формуле:  (бит) (бит)Теперь рассчитаем количество информации, которое получится при бросании симметричной и однородной четырехгранной пирамидки:  (бит) (бит)Формула Шеннона:  , где , где 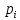 -вероятность того, что именно i-е сообщение выделено в наборе из N сообщений. -вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.Легко заметить, что если вероятности 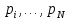 равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли. равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли. Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями. В качестве единицы информации Клод Шеннон предложил принять один бит (англ. bit — binary digit — двоичная цифра). Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений (типа "орел"—"решка", "чет"—"нечет" и т.п.). В вычислительной технике битом называют наименьшую "порцию" памяти компьютера, необходимую для хранения одного из двух знаков "0" и "1", используемых для внутримашинного представления данных и команд. Бит — слишком мелкая единица измерения. На практике чаще применяется более крупная единица — байт, равная восьми битам. Именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=28). Широко используются также ещё более крупные производные единицы информации: 1 Килобайт (Кбайт) = 1024 байт = 210байт 1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт, 1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт. В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как: 1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт, 1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт. За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации. Алфавитный подход к определению информацию. При определении количества информации на основе уменьшения неопределенности наших знаний мы рассматриваем информацию с точки зрения содержания, ее понятности и новизны для человека. С этой точки зрения в опыте по бросанию монеты одинаковое количество информации содержится и в зрительном образе упавшей монеты, и в коротком сообщении «Орел», и в длинной фразе «Монета упала на поверхность земли той стороной вверх, на которой изображен орел». Однако при хранении и передаче информации с помощью технических устройств целесообразно отвлечься от содержания информации и рассматривать ее как последовательность знаков (букв, цифр, кодов цветов точек изображения и так далее). Набор символов знаковой системы (алфавит) можно рассматривать как различные возможные состояния (события). Тогда, если считать, что появление символов в сообщении равновероятно, по формуле N=2I можно рассчитать, какое количество информации несет каждый символ. Так, в русском алфавите, если не использовать букву ё, количество событий (букв) будет равно 32. Тогда: 32=2I откуда I=5 битов. Каждый символ несет 5 битов информации (его информационная емкость равна 5 битов). Количество информации в сообщении можно подсчитать, умножив количество информации, которое несет один символ, на количество символов. Количество информации, которое содержит сообщение, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на количество знаков. Задача 3. Книга, набранная с помощью компьютера, содержит 150 страниц, на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге? Решение. 40 60 150 =360000 символов в книге = 360000 байт. 360000 байт = 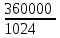 = 351,5625 Кб = = 351,5625 Кб = 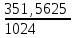 = 0,34332275Мб. = 0,34332275Мб.Объем книги 0,34 Мб. Задача 4. Сколько килобайт составляет сообщение, содержащее 12288 бит? Решение. 12288 / 8 / 1024 = 1,5 Кб. Задача 5. Можно ли уместить на одну дискету книгу, имеющую 432 страницы, причем на каждой странице этой книги 46 строк, а в каждой строке 62 символа? Решение. 46 62 432 =1 232 064 символов в книге = 1 232 064 байт. 1 232 064 байт = 1,17 Мб. Емкость дискеты 1,44 Мб, значит, книга может поместиться на одну дискету. Задача 6. Сообщение, записанное буквами из 64-символьного алфавита, содержит 20 символов. Какой объем информации оно несет? Решение. 20i = 64, i = 6 бит – количество информации, которое несет каждый символ, 20 6 = 120 бит = 15 байт. Задача 7. Одно племя имеет 32-символьный алфавит, а второе племя – 64-символьный алфавит. Вожди племен обменялись письмами. Письмо первого племени содержало 80 символов, а письмо второго племени – 70 символов. Сравните объем информации, содержащийся в письмах. Решение. Первое племя: 2i = 32, i = 5 бит – количество информации, которое несет каждый символ, 5 80 = 400 бит. Второе племя: 2i = 64, i = 6 бит – количество информации, которое несет каждый символ, 6 70 = 420 бит. Значит, письмо второго племени содержит больше информации. Задача 8. Информационное сообщение объемом 1,5 Кб содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение? Решение. I = 1,5 Кб = 1,5 1024 = 1536 байта = 1536 8 = 12288 бит. i = 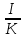 = = 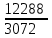 = 4 бита. = 4 бита.N = 2i = 24 = 16 символов. Задача 9. Объем сообщения, содержащего 2048 символов, составил 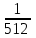 Мб. Каков размер алфавита, с помощью которого записано сообщение? Мб. Каков размер алфавита, с помощью которого записано сообщение?Решение. I = 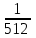 Мб = Мб = 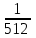 1024 1024 8 = 16384 бит. 1024 1024 8 = 16384 бит.i = 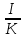 = = 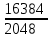 = 8 бит. = 8 бит.N = 2i = 28 = 256 символов. Задача 8. Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если объем этого сообщения составил 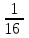 Мб. Мб.Решение. I = 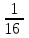 Мб = Мб = 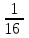 1024 1024 8 = 524 288 бит. 1024 1024 8 = 524 288 бит.N = 16 = 2i, i = 4 бита. K =  = = 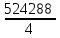 = 131 072 символа. = 131 072 символа. Задача 9. Для записи сообщения использовался 64-символьный алфавит. Каждая страница содержит 30 строк. Все сообщение содержит 8775 байт информации и занимает 6 страниц. Сколько символов в строке? Решение. I = 8775 байт = 8775 8 = 70 200 бит. N = 64 = 2i , i = 6 бит. Объем информации одной страницы книги = = 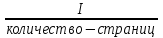 = =  = 11 700бит. = 11 700бит.Количество символов в строке: 11 700 бит / 6 бит / 30 строк = 65 символов. Задача 10. ДНК человека (генетический код) можно представить себе как некоторое слово в четырехбуквенном алфавите, где каждой буквой помечается звено цепи ДНК (нуклеотид). Сколько информации в битах содержит цепочка ДНК человека, содержащая примерно 1,51023 нуклеотидов? Решение. N = 4 = 2i , i = 2 бита. I = K i = 1,5 1023 2 = 3 1023 бита. Данные и их кодирование. Принципы кодирования и декодирования. Представление информации происходит в различных формах в процессе восприятия окружающей среды живыми организмами и человеком, в процессах обмена информацией между человеком и человеком, человеком и компьютером, компьютером и компьютером и так далее. Преобразование информации из одной формы представления (знаковой системы) в другую называется кодированием. Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем. В процессе обмена информацией часто приходится производить операции кодирования и декодирования информации. При вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на клавиатуре происходит кодирование знака, то есть преобразование его в компьютерный код. При выводе знака на экран монитора или принтер происходит обратный процесс — декодирование, когда из компьютерного кода знак преобразуется в его графическое изображение. Кодирование — это операция преобразования знаков или групп знаков одной знаковой системы в знаки или группы знаков другой знаковой системы. Рассмотрим в качестве примера кодирования соответствие цифрового и штрихового кодов товара. Такие коды имеются на каждом товаре и позволяют полностью идентифицировать товар (страну и фирму производителя, тип товара и др.).  Рисунок 2. Знакам цифрового кода (цифрам) соответствуют группы знаков штрихового кода (узкие и широкие штрихи, а также размеры промежутков между ними) — рис.2. Для человека удобен цифровой код, а для автоматизированного учета — штриховой код, который считывается с помощью узкого светового луча и подвергается последующей обработке в компьютерных бухгалтерских системах учета. Аналоговый и дискретный способы представления информации. Человек способен воспринимать и хранить информацию в форме образов (зрительных, звуковых, осязательных, вкусовых и обонятельных). Зрительные образы могут быть сохранены в виде изображений (рисунков, фотографий и так далее), а звуковые — зафиксированы на пластинках, магнитных лентах, лазерных дисках и так далее. Информация, в том числе графическая и звуковая, может быть представлена в аналоговой или дискретной форме. При аналоговом представлении физическая величина принимает бесконечное множество значений, причем ее значения изменяются непрерывно. При дискретном представлении физическая величина принимает конечное множество значений, причем ее величина изменяется скачкообразно. Приведем пример аналогового и дискретного представления информации. Положение тела на наклонной плоскости и на лестнице задается значениями координат X и У. При движении тела по наклонной плоскости его координаты могут принимать бесконечное множество непрерывно изменяющихся значений из определенного диапазона, а при движении по лестнице — только определенный набор значений, причем меняющихся скачкообразно. 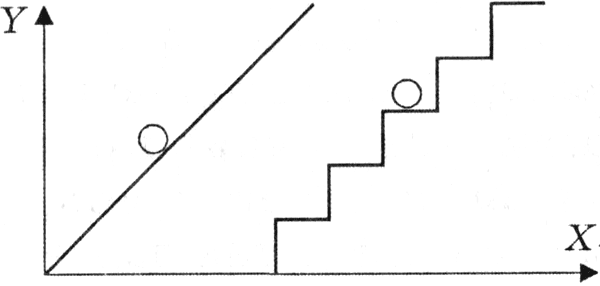 Рисунок 3. Примером аналогового представления графической информации может служить, например, живописное полотно, цвет которого изменяется непрерывно, а дискретного — изображение, напечатанное с помощью струйного принтера и состоящее из отдельных точек разного цвета. Примером аналогового хранения звуковой информации является виниловая пластинка (звуковая дорожка изменяет свою форму непрерывно), а дискретного — аудиокомпакт-диск (звуковая дорожка которого содержит участки с различной отражающей способностью). Преобразование графической и звуковой информации из аналоговой формы в дискретную производится путем дискретизации, то есть разбиения непрерывного графического изображения и непрерывного (аналогового) звукового сигнала на отдельные элементы. В процессе дискретизации производится кодирование, то есть присвоение каждому элементу конкретного значения в форме кода. Дискретизация — это преобразование непрерывных изображений и звука в набор дискретных значений в форме кодов. Кодирование дискретной и аналоговой информации. Структурная схема одноканальной системы передачи информации приведена на рис. 4. Информация поступает в систему в форме сообщений. Под сообщением понимают совокупность знаков или первичных сигналов, содержащих информацию. Источник сообщений в общем случае образует совокупность источника информации (исследуемого или наблюдаемого объекта) и первичного преобразователя (датчика, человека-оператора и т.п.), воспринимающего информацию о его состояниях или протекающем в нем процессе. Различают дискретные и непрерывные сообщения. 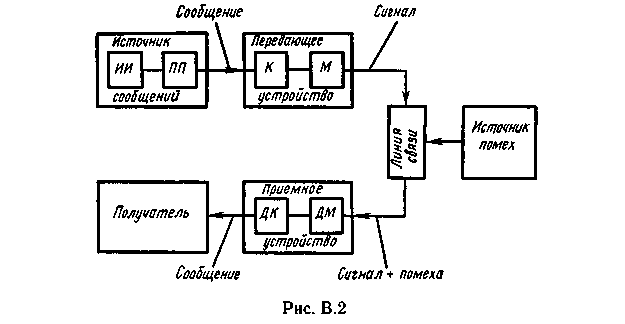 Рисунок 4. Дискретные сообщения формируются в результате последовательной выдачи источником отдельных элементов - знаков. Множество различных знаков называют алфавитом источника сообщений, а число знаков - объемом алфавита. В частности, знаками могут быть буквы естественного или искусственного языка, удовлетворяющие определенным правилам взаимосвязи. Распространенной разновидностью дискретных сообщений являются данные. Непрерывные сообщения не разделимы на элементы. Они описываются функциями времени, принимающими непрерывное множество значений. Типичными примерами непрерывных сообщений могут служить речь, телевизионное изображение. В ряде систем связи непрерывные сообщения с целью повышения качества передачи преобразуются в дискретные. Для передачи сообщения по каналу связи ему необходимо поставить в соответствие определенный сигнал. В информационных системах под сигналом понимают физический процесс, отображающий (несущий) сообщение. Преобразование сообщения в сигнал, удобный для передачи по данному каналу связи, называют кодированием в широком смысле слова. Операцию восстановления сообщения по принятому сигналу называют декодированием. Так как число возможных дискретных сообщений при неограниченном увеличении времени стремится к бесконечности, а за достаточно большой промежуток времени весьма велико, то ясно, что создать для каждого сообщения свой сигнал практически невозможно. Однако, поскольку дискретные сообщения складываются из знаков, имеется возможность обойтись конечным числом образцовых сигналов, соответствующих отдельным знакам алфавита источника. Для обеспечения простоты и надежности распознавания образцовых сигналов их число целесообразно сократить до минимума. Поэтому, как правило, прибегают к операции представления исходных знаков в другом алфавите с меньшим числом знаков, называемых символами. При обозначении этой операции используется тот же термин "кодирование", рассматриваемый в узком смысле. Устройство, выполняющее такую операцию, называют кодирующим или кодером К. Так как алфавит символов меньше алфавита знаков, то каждому знаку соответствует некоторая последовательность символов, которую назовем кодовой комбинацией. Число символов в кодовой комбинации называют ее значностью, число ненулевых символов - весом. Аналогично, для операции сопоставления символов со знаками исходного алфавита используется термин "декодирование". Техническая реализация ее осуществляется декодирующим устройством или декодером ДК. В простейшей системе связи кодирующее, а следовательно, и декодирующее устройство может отсутствовать. Передающее устройство осуществляет преобразование непрерывных сообщений или знаков в сигналы, удобные для прохождения по конкретной линии связи (либо для хранения в некотором запоминающем устройстве). При этом один или несколько параметров выбранного носителя изменяют в соответствии с передаваемой информацией. Такой процесс называют модуляцией. Он осуществляется модулятором М. Обратное преобразование сигналов в символы производится демодулятором ДМ. Под линией связи понимают любую физическую среду (воздух, металл, магнитную ленту и т.п.), обеспечивающую поступление сигналов от передающего устройства к приемному. Сигналы на выходе линии связи могут отличаться от переданных вследствие затухания, искажения и воздействия помех. Помехами называют любые мешающие возмущения, как внешние (атмосферные помехи, промышленные помехи), так и внутренние (источником которых является сама аппаратура связи), вызывающие случайные отклонения принятых сигналов от переданных. Эффект воздействия помех на различные блоки системы стараются учесть эквивалентным изменением характеристик линии связи. Поэтому источник помех условно относят к линии связи. Из смеси сигнала, и помехи приемное устройство выделяет сигнал и посредством декодера восстанавливает Сообщение, которое в общем случае может отличаться от посланного. Меру соответствия принятого сообщения посланному называют верностью передачи. Обеспечение заданной верности передачи сообщений - важнейшая цель системы связи. Принятое сообщение с выхода системы связи поступает к абоненту-получателю, которому была адресована исходная информация. Совокупность средств, предназначенных для передачи сообщений, называют каналом связи. Для передачи информации от группы источников, сосредоточенных в одном пункте, к группе получателей, расположенных в другом пункте, часто целесообразно использовать только одну линию связи, организовав на ней требуемое число каналов. Такие системы называют многоканальными. Кодирование и обработка звуковой информации Звуковая информация. Звук представляет собой распространяющуюся в воздухе, воде или другой среде волну с непрерывно меняющейся интенсивностью и частотой. Человек воспринимает звуковые волны (колебания воздуха) с помощью слуха в форме звука различных громкости и тона. Чем больше интенсивность звуковой волны, тем громче звук, чем больше частота волны, тем выше тон звука (рис. 5).
Человеческое ухо воспринимает звук с частотой от 20 колебаний в секунду (низкий звук) до 20 000 колебаний в секунду (высокий звук). Человек может воспринимать звук в огромном диапазоне интенсивностей, в котором максимальная интенсивность больше минимальной в 1014 раз (в сто тысяч миллиардов раз). Для измерения громкости звука применяется специальная единица "децибел"(дбл) (табл.8). Уменьшение или увеличение громкости звука на 10 дбл соответствует уменьшению или увеличению интенсивности звука в 10 раз.
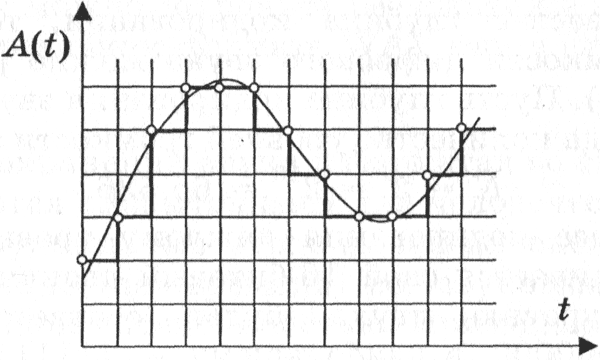
Временная дискретизация звука. Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть преобразован в цифровую дискретную форму с помощью временной дискретизации. Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, для каждого такого участка устанавливается определенная величина интенсивности звука. Таким образом, непрерывная зависимость громкости звука от времени A(t) заменяется на дискретную последовательность уровней громкости. На графике это выглядит как замена гладкой кривой на последовательность "ступенек" (рис. 6).
Частота дискретизации. Для записи аналогового звука и его преобразования в цифровую форму используется микрофон, подключенный к звуковой плате. Качество полученного цифрового звука зависит от количества измерений уровня громкости звука в единицу времени, т. е. частоты дискретизации. Чем большее количество измерений производится за I секунду (чем больше частота дискретизации), тем точнее "лесенка" цифрового звукового сигнала повторяет кривую диалогового сигнала. Частота дискретизации звука - это количество измерений громкости звука за одну секунду. Частота дискретизации звука может лежать в диапазоне от 8000 до 48 000 измерений громкости звука за одну секунду. Глубина кодирования звука. Каждой "ступеньке" присваивается определенное значение уровня громкости звука. Уровни громкости звука можно рассматривать как набор возможных состояний N, для кодирования которых необходимо определенное количество информации I, которое называется глубиной кодирования звука. Глубина кодирования звука - это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука. Если известна глубина кодирования, то количество уровней громкости цифрового звука можно рассчитать по формуле N = 2I. Пусть глубина кодирования звука составляет 16 битов, тогда количество уровней громкости звука равно: N = 2I = 216 = 65 536. В процессе кодирования каждому уровню громкости звука присваивается свой 16-битовый двоичный код, наименьшему уровню звука будет соответствовать код 0000000000000000, а наибольшему - 1111111111111111. Качество оцифрованного звука. Чем больше частота и глубина дискретизации звука, тем более качественным будет звучание оцифрованного звука. Самое низкое качество оцифрованного звука, соответствующее качеству телефонной связи, получается при частоте дискретизации 8000 раз в секунду, глубине дискретизации 8 битов и записи одной звуковой дорожки (режим "моно"). Самое высокое качество оцифрованного звука, соответствующее качеству аудио-CD, достигается при частоте дискретизации 48 000 раз в секунду, глубине дискретизации 16 битов и записи двух звуковых дорожек (режим "стерео"). Необходимо помнить, что чем выше качество цифрового звука, тем больше информационный объем звукового файла. Можно оценить информационный объем цифрового стереозвукового файла длительностью звучания 1 секунда при среднем качестве звука (16 битов, 24 000 измерений в секунду). Для этого глубину кодирования необходимо умножить на количество измерений в 1 секунду й умножить на 2 (стереозвук): 16 бит × 24 000 × 2 = 768 000 бит = 96 000 байт = 93,75 Кбайт. Звуковые редакторы. Звуковые редакторы позволяют не только записывать и воспроизводить звук, но и редактировать его. Оцифрованный звук представляется в звуковых редакторах в наглядной форме, поэтому операции копирования, перемещения и удаления частей звуковой дорожки можно легко осуществлять с помощью мыши. Кроме того, можно накладывать звуковые дорожки друг на друга (микшировать звуки) и применять различные акустические эффекты (эхо, воспроизведение в обратном направлении и др.). Звуковые редакторы позволяют изменять качество цифрового звука и объем звукового файла путем изменения частоты дискретизации и глубины кодирования. Оцифрованный звук можно сохранять без сжатия в звуковых файлах в универсальном формате WAV или в формате со сжатием МР3. При сохранении звука в форматах со сжатием отбрасываются "избыточные" для человеческого восприятия звуковые частоты с малой интенсивностью, совпадающие по времени со звуковыми частотами с большой интенсивностью. Применение такого формата позволяет сжимать звуковые файлы в десятки раз, однако приводит к необратимой потере информации (файлы не могут быть восстановлены в первоначальном виде). Теорема Котельникова и ее применение Теоре́ма Коте́льникова (в англоязычной литературе — теорема Найквиста — Шеннона или теорема отсчётов) гласит, что, если аналоговый сигнал имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой строго большей удвоенной максимальной частоты спектра : Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временно́й характеристике точек разрыва. Именно это подразумевает понятие «спектр, ограниченный частотой fc». Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и, обычно, имеют во временно́й характеристике разрывы. Соответственно, их спектр бесконечен. В таком случае полное восстановление сигнала невозможно и из теоремы Котельникова вытекают 2 следствия: Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой f> 2fc, где fc — максимальная частота, которой ограничен спектр реального сигнала. Если максимальная частота в сигнале превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует. Говоря шире, теорема Котельникова утверждает, что непрерывный сигнал 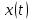 можно представить в виде интерполяционного ряда можно представить в виде интерполяционного ряда Где  — функция sinc. Интервал дискретизации удовлетворяет ограничениям — функция sinc. Интервал дискретизации удовлетворяет ограничениям 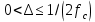 Мгновенные значения данного ряда есть дискретные отсчёты сигнала Мгновенные значения данного ряда есть дискретные отсчёты сигнала 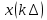 . .При оцифровке или дискретизации аналогового сигнала X(t) происходит замена непрерывной функции U=U(t) на интервале [t1, t2] ломанной с большим количеством маленьких звеньев (ступенек). Это осуществляется путем развертки по времени оси квантования по величине. Длительность ступенек равна шагу квантования по времени dt=1/f, где f -- частота отсчетов, а их величина кратна шагу квантования по величине dU. Величина каждой ступеньки представляется в двоичном коде, в результате чего получается массив x={x1, x2, ... , xn} Теорема отсчетов В.А.Котельникова (1933 г.): Непрерывный сигнал может быть оцифрован и воссоздан без потери информации, если шаг развертки по времени не превышает половину периода максимальной гармоники сигнала: dt<1/2fmax. Например, для оцифровки речевого сигнала с частотой до 5 кГц, частота отсчетов должна быть не менее 10 кГц. Теорема квантования по величине: Для качественной оцифровки и воспроизведения непрерывного сигнала достаточно, чтобы шаг квантования по величине был меньше чувствительности приемного устройства dU. Если глаз человека (приемник) различает 16 миллионов цветовых оттенков, то при квантовании цвета не имеет смысла делать больше градаций. Преимущества цифрового представления сигнала: высокая помехоустойчивость, универсальность, простота и надежность устройств, обрабатывающих информацию. Характеристика процесса передачи данных. Каналы передачи данных. Способы передачи информации. Американским ученым, одним из основателей теории информации, Клодом Шенноном была предложена схема процесса передачи информации по техническим каналам связи, представленная на рисунке 27: 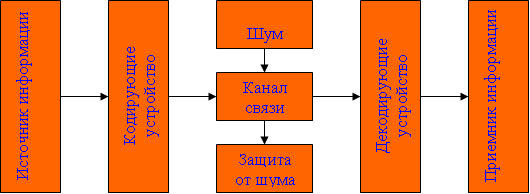 |