Учебное пособие Курск 2016
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
Двоичная система счисления. Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0. Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ. Восьмеричная система счисления. Для записи чисел используется восемь чисел 0,1,2,3,4,5,6,7. Шестнадцатеричная система счисления. Для записи чисел в шестнадцатеричной системе необходимо располагать уже шестнадцатью символами, используемыми как цифры. В качестве первых десяти используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной они соответствуют числам 10,11,12,13,14,15) используются буквы латинского алфавита – A,B,C,D,E,F. Перевод целых чисел из десятичной системы счисления в другую. Правило перевода целых чисел из десятичной системы счисления в систему с основанием q: Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх). Пример 5. Перевести 2610 в двоичную систему счисления. Решение:  Ответ: 2610=110102 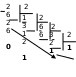 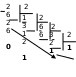 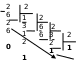 Пример 6. Перевести 24110 в восьмиричную систему счисления. А10→А8 Пример 6. Перевести 24110 в восьмиричную систему счисления. А10→А8Решение: 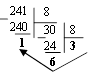 Ответ: 24110=3618 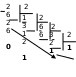 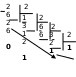 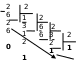     Пример 7. Перевести 362710 в восьмиричную систему счисления. А10→А8 Пример 7. Перевести 362710 в восьмиричную систему счисления. А10→А8Решение: 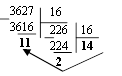 Т.к. в шестнадцатеричной системе счисления 14 – Е, а 11 – В, то получаем ответ Е2В16. Перевод дробных чисел из десятичной системы счисления в другую. Правило перевода дробных чисел из десятичной системы счисления в систему с основанием q: Последовательно выполнять умножение исходного числа и получаемых дробные части на q до тех пор, пока дробная часть не станет равна нулю или не достигнем требуемую точность. Полученные при таком умножении целые части - числа в системе счисления q – записать в прямом порядке (сверху вниз). Пример 8. Перевести 0,562510 в двоичную систему счисления. А10→А2 Решение: 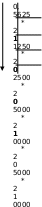 Ответ: 0,562510=0,10012 Пример 9. Перевести 0,562510 восьмеричную систему счисления. А10→А8 Решение:  Ответ: 0,562510=0,528 Пример 10. Перевести 0,66510 в двоичную систему счисления. А10→А2 Решение:   Процесс умножения может продолжаться до бесконечности. Тогда его прерывают на некотором шаге, когда считают, что получена требуемая точность представления числа Ответ: 0,66510=0,100012 Перевод произвольных чисел из десятичной системы счисления в другую. Перевод произвольных чисел, то есть чисел, содержащих целую и дробную части, осуществляют в два этапа. Отдельно переводится целая часть, отдельно – дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой. Перевод чисел из любой системы счисления в десятичную. Правило Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления. Пример 11. Перевести число 1101102 из двоичной системы счисления в десятичную. Решение: 5 4 3 2 1 0 1 1 0 1 1 0 2 = 1*25 + 1*24 + 0*23+1*22+1*21+0*20 =32+16+4+2=5410 Ответ: 1101102 = 5410 Пример 12. Перевести число 101,012 из двоичной системы счисления в десятичную. Решение: 2 1 0 -1 -2 1 0 1,0 1 2 = 1*22 + 0*21 + 1*20+0*2-1+1*2-2 =4+0+1+0+0,25=5,2510 Ответ: 101,012 = 5,2510 Пример 13. Перевести число 1221003 из троичной системы счисления в десятичную. Решение: 4 3 2 1 0 1 2 2 0 1 3=1*34 + 2*33 + 2*32 + 0*31 + 1*30 = 81+54+18+1 = 15410 Ответ: 122013 = 15410 Пример 14. Перевести число 1637 из семеричной системы счисления в десятичную. Решение: 1637 = 1*72 + 6*71 + 3*70 = 49+42+3= 9410. Ответ: 1637 = 9410. Пример 15. Перевести число 234,68 из восьмеричной системы в десятичную: Решение: 2 1 0 -1 2 3 4, 68 = 2*82 +3*81 + 4*80 +6*8-1= 2*64+3*8+4+6*0,125= 128+24+4+0,75 =156,7510 Ответ: 234,68 = 156,7510. Пример 16. Перевести число 2Е16 в десятичную систему счисления. Решение: 2 1 2 Е16 = 2*161 +14*160 = 32 +14 = 4610. Ответ: 2Е16 = 4610. Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления. Перевод целых чисел. Правило Чтобы перевести целое двоичное число в восьмеричную (8=23) систему счисления необходимо: разбить данное число справа налево на группы по 3 цифры в каждой; рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной системы счисления. Пример 17. Перевести число 111010102 в восьмеричную систему счисления. Решение: 11101010 3 5 2  Ответ: 111010102 = 3528 Правило Чтобы перевести целое двоичное число в шестнадцатеричную (16=24) систему счисления необходимо: разбить данное число справа налево на группы по 4 цифры в каждой; рассмотреть каждую группу и записать ее соответствующей цифрой шестнадцатеричной системы счисления. Пример 18. Перевести число 111000102 в шестнадцатеричную систему счисления. Решение: 11100010 Е 2  Ответ: 111000102 = Е216 Перевод дробных чисел. Правило Чтобы перевести дробное двоичное число в восьмеричную (шестнадцатеричную) систему счисления необходимо: разбить данное число, начиная от запятой влево целую часть и вправо дробную часть на группы по 3 (4) цифры в каждой; рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной (шестнадцатеричной)системы счисления. Пример 19. Перевести число 0,101100001112 в шестнадцатеричную систему счисления. Решение: 0,10110000111 В 0 7  Ответ: 0,101100001112 = В0716 Приме 20. Перевести число 111100001,01112 в восьмеричную систему счисления. Решение: 111100001,0111 7 4 1 3 1  Ответ: 111100001,01112= 741,318 Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления. Правило Для того, чтобы восьмеричное (шестнадцатеричное) число перевести в двоичную систему счисления, необходимо каждую цифру этого числа заменить соответствующим числом, состоящим из 3 (4) цифр двоичной системы счисления. Пример 21. Перевести число 5288 перевести в двоичную систему счисления. Решение: 5 2 3 101 010 011  Ответ: 5288 = 1010100112 Пример 22. Перевести число 4ВА35,1С216 перевести в двоичную систему счисления. Решение: 4 В А 3 5 , 1 С 2 100 1011 101000110101 0001 1100 0010  Ответ: 4ВА35,1С216 = 10010111010001101010001 110000102 Арифметические операции в системах счисления Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам. Правила выполнения арифметических операций в десятичной системе хорошо известны - это сложение, вычитание, умножение столбиком и деление уголком. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы. Таблицы сложения в любой позиционной системе счисления легко составить, используя правило счета: Если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. Таблица 5. Сложение в двоичной системе. 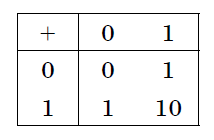 Таблица 6. Сложение в восьмеричной системе. 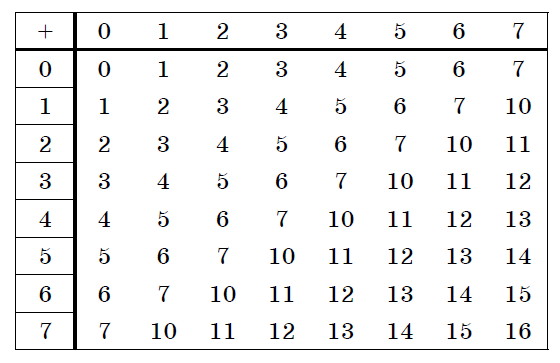 Пример 23. Сложим числа 15 и 6 в различных системах счисления. Решение. Переведем числа 15 и 6в двоичную и восьмеричную системы счисления и выполним сложение, используя таблицы сложения (см. выше).  Ответ: 15+6=2110=101012=258 Пример 24. Вычислим сумму чисел 438 и 5616. Результат представим в восьмеричной системе счисления. Решение. Переведем число 5616 в восьмеричную систему счисления, используя поразрядный способ перевода разложением на тэтрады и триады: 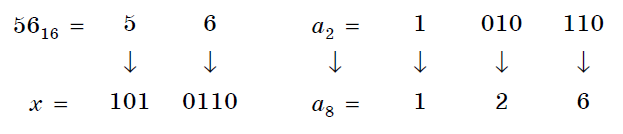 Пользуясь правилами сложения в восьмеричной системе счисления, получаем: 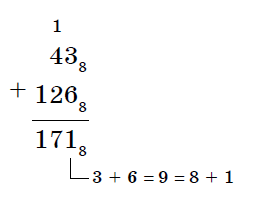 Ответ: 438 + 5616 = 1718 Вычитание осуществляется по тем же правилам, что и в десятичной системе счисления. При вычитании из меньшего числа большего производится заем из старшего разряда. Пример 25. Вычислим разность X−Y двоичных чисел, если X=10101002 и Y=10000102. Результат представим в двоичном виде. Решение: 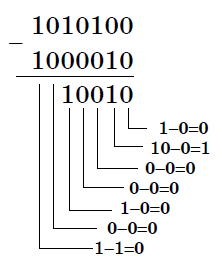 Ответ: 100102 Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения. Таблица 7. Умножение в двоичной системе. 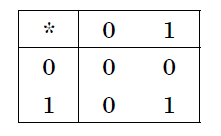 Таблица 8. Умножение в восьмеричной системе. 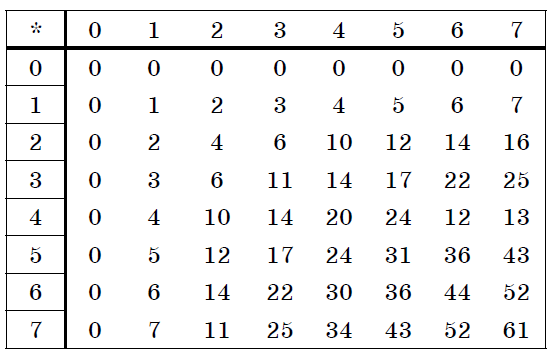 Умножение многоразрядных чисел в различных позиционных системах счисления происходит по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя. Пример 26. Перемножим числа 15 и 12.  Ответ: 15⋅12=18010=101101002=2648 Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. Следует только грамотно пользоваться теми цифрами, которые входят в алфавит используемой системы счисления. Понятие количества информации. Единицы измерения информации. Какое количество информации содержится, к примеру, в тексте романа "Война и мир", во фресках Рафаэля или в генетическом коде человека? Ответа на эти вопросы наука не даёт и, по всей вероятности, даст не скоро. А возможно ли объективно измерить количество информации? Важнейшим результатом теории информации является следующий вывод: В определенных, весьма широких условиях можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных. В настоящее время получили распространение подходы к определению понятия "количество информации", основанные на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте. Эти подходы используют математические понятия вероятности и логарифма. Объём информации можно представлять как логарифм[2]количества возможных состояний. Наименьшее целое число, логарифм которого положителен — это 2. Соответствующая ему единица — бит — является основой исчисления ин-формации в цифровой технике. Единица, соответствующая числу 3 (трит) равна log23≈1,585 бита, числу 10 (хартли) — log210≈3.322 бита. Такая единица как нат (nat), соответствующая натуральному логарифму применяется в инженерных и научных расчётах. В вычислительной технике она практически не применяется, так как основание натуральных логарифмов не является целым числом. Единицы, производные от бита Целые количества бит отвечают количеству состояний, равному степеням двойки. Особое название имеет 4 бита — ниббл (полубайт, тетрада, четыре двоичных разряда), которые вмещают в себя количество информации, со-держащейся в одной шестнадцатеричной цифре. Байт Следующей по порядку популярной единицей информации является 8 бит, или байт (о терминологических тонкостях написано ниже). Именно к байту (а не к биту) непосредственно приводятся все большие объёмы информации, исчисляемые в компьютерных технологиях. Такие величины как машинное слово и т. п., составляющие несколько байт, в качестве единиц измерения почти никогда не используются. Килобайт Для измерения больших количеств байтов служат единицы «килобайт» = [1024] байт и «Кбайт»[3] (кибибайт, kibibyte) = 1024 байт (о путанице десятичных и двоичных единиц и терминов см. ниже). Такой порядок величин имеют, например: Сектор диска обычно равен 512 байтам то есть половине килобайта, хотя для некоторых устройств может быть равен одному или двум кибибайт. Классический размер «блока» в файловых систе-мах UNIX равен одному Кбайт (1024 байт). «Страница памяти» в процессорах x86 (начиная с моде-ли Intel 80386) имеет размер 4096 байт, то есть 4 Кбайт. Объём информации, получаемой при считывании дискеты «3,5″ высокой плотности» равен 1440 Кбайт (ровно); другие форматы также исчисляются целым числом Кбайт. Мегабайт Единицы «мегабайт» = 1024 килобайт = [1048576] байт и «Мбайт» (мебибайт, mebibyte) = 1024 Кбайт = 1 048 576 байт применяются для измерения объёмов носителей информации. Объём адресного пространства процессора Intel 8086 был равен 1 Мбайт. Оперативную память и ёмкость CD-ROM меряют двоичными единицами (мебибайтами, хотя их так обычно не называют), но для объёма НЖМД десятичные мегабайты были более популярны. Современные жёсткие диски имеют объёмы, выражаемые в этих единицах минимум шестизначными числами, поэтому для них применяются гигабайты. Следующей по порядку популярной единицей информации является 8 бит, или байт (о терминологических тонкостях написано ниже). Именно к байту (а не к биту) непосредственно приводятся все большие объёмы информации, исчисляемые в компьютерных технологиях. Такие величины как машинное слово и т. п., составляющие не-сколько байт, в качестве единиц измерения почти никогда не используются. Гигабайт Единицы «гигабайт» = 1024 мегабайт = [1048576] килобайт = [1073741824] байт и «Гбайт» (гибибайт, gibibyte) = 1024 Мбайт = 230байт измеряют объём больших носителей информации, например жёстких дисков. Разница между двоичной и десятичной единицами уже превышает 7 %. Размер 32-битного адресного пространства равен 4 Гбайт ≈ 4,295 Мбайт. Такой же порядок имеют размер DVD-ROM и современных носителей на флэш-памяти. Размеры жёстких дисков уже достигают сотен и тысяч гигабайт. Для исчисления ещё больших объёмов информации имеются единицы терабайт и тебибайт (1012 и 240 байт соответствен-но),петабайт и пебибайт (1015 и 250 байт соответственно) и т. д. Байт определяется для конкретного компьютера как минимальный шаг адресации памяти, который на старых машинах не обязательно был равен 8 битам (а память не обязательно состоит из битов — см., например: троичный компьютер). В современной традиции, байт часто считают равным восьми битам. В таких обозначениях как байт (русское) или B (английское) под байт (B) подразумевается именно 8 бит, хотя сам термин «байт» не вполне корректен с точки зрения теории. Во французском языке используются обозначения o, Ko, Mo и т. д. (от слова octet) дабы подчеркнуть, что речь идёт именно о 8 битах. Долгое время разнице между множителями 1000 и 1024 старались не придавать большого значения. Во избежание недоразумений следует чётко понимать различие между: двоичными кратными единицами, обозначаемыми соглас-но ГОСТ 8.417-2002 как «Кбайт», «Мбайт», «Гбайт» и т. д. (два в степенях кратных десяти); единицами килобайт, мегабайт, гигабайт и т. д., понимаемыми как научные термины (десять в степенях, кратных трём),эти единицы по определению равны, соответственно, 103, 106, 109 байтам и т. д. В качестве терминов для «Кбайт», «Мбайт», «Гбайт» и т. д. МЭК предлагает «кибибайт», «мебибайт», «гибибайт» и т. д., однако эти термины критикуются за непроизносимость и не встречаются в устной речи. В различных областях информатики предпочтения в употреблении десятичных и двоичных единиц тоже различны. Причём, хотя со времени стандартизации терминологии и обозначений прошло уже несколько лет, далеко не везде стремятся прояснить точное значение используемых единиц. В английском языке для «киби»=1024 иногда используют прописную букву K, дабы подчеркнуть отличие от обозначаемой строчной бук-вой приставки СИ кило. Однако, такое обозначение не опирается на авторитетный стандарт, в отличие от российского ГОСТа касательно «Кбайт». Формула Хартли. Методы и средства определения количества информации. Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N. Формула Хартли: I = log2N Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2100 = 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации. |
