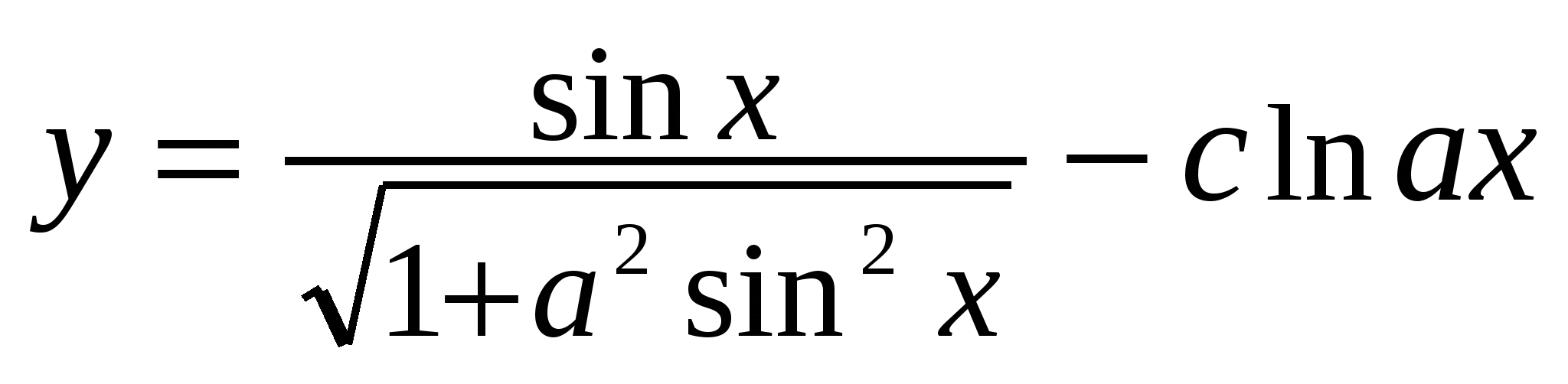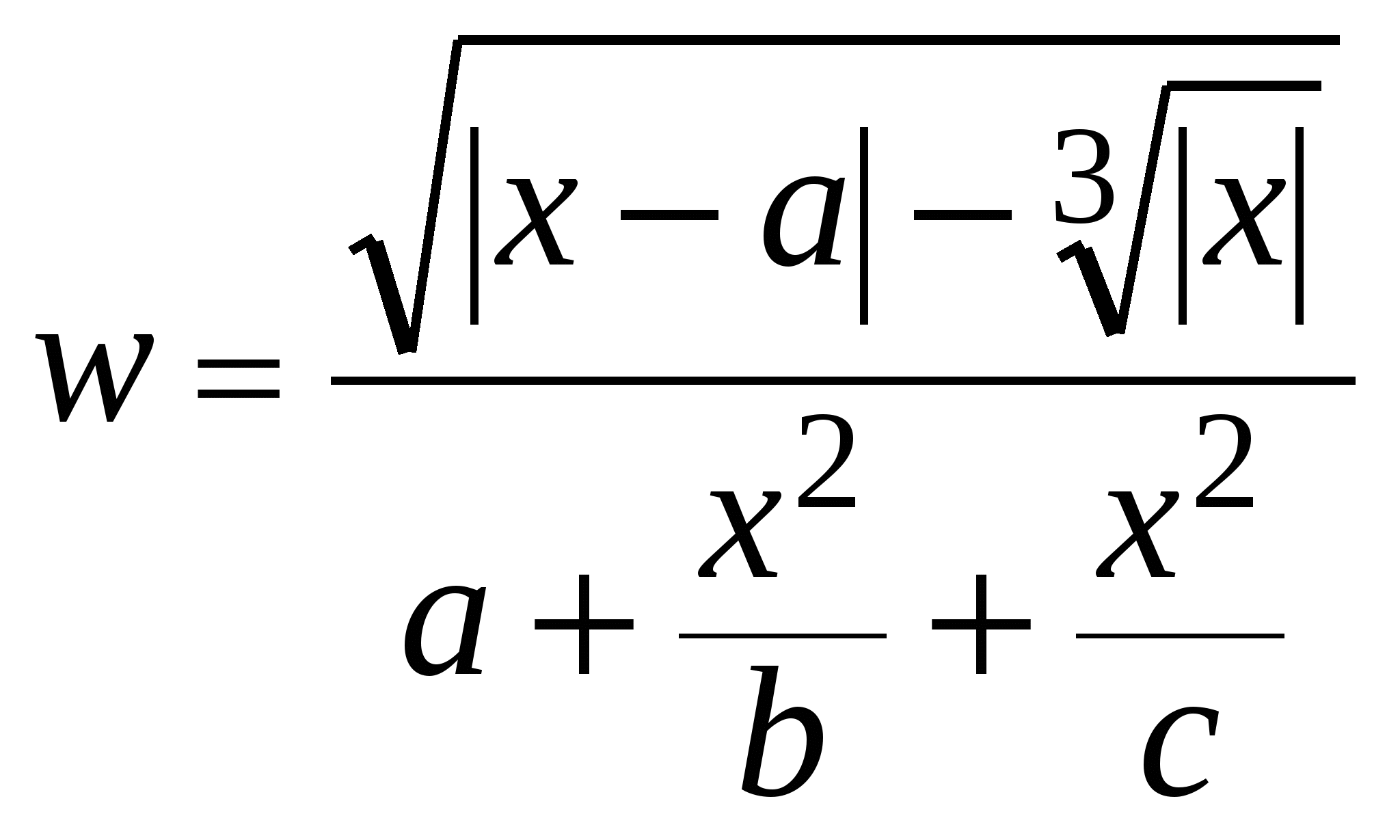Учебное пособие Омск Издательство Омгту 2010 удк 004. 4 (075) ббк 32. 973018я73 ч 49 Рецензенты
 Скачать 1.07 Mb. Скачать 1.07 Mb.
|
Приоритеты операций в выражении
К бинарным относятся арифметические операции, применяемые к двум операндам: умножение ( * ), деление ( / ), целочисленное деление ( DIV), остаток от целочисленного деления (MOD), сложение (+) и вычитание ( - ). К унарным относятся арифметические операции, применяемые к одному операнду: операции + и – для целых вещественных чисел. При выполнении целочисленного деления операцией DIV результатом является целая часть частного (остаток отбрасывается), например: 15 DIV 4 = 3. В случае применения операции MOD результатом является остаток от деления левого на правый операнд (оба операнда целые), например: 11 MOD 3 = 2. Согласно общим правилам вычисления в первую очередь вычисляются выражения, заключенные в круглые скобки, а затем вычисляются значения функций, входящих в выражение. В арифметических выражениях без скобок вычисления выполняются в соответствии с приоритетом операций (табл. 1), т.е. сначала выполняется унарная операция (унарный минус), затем операции умножения и деления ( *, /, div, mod) и в последнюю очередь операции сложения и вычитания ( +, - ) . 3.2. Оператор присваивания Как и во всех языках программирования, в Pascal ABC имеется оператор присваивания. Он служит для определения или переопределения значения переменной. В случае переопределения старое значение переменной стирается и записывается новое значение. Структура оператора присваивания имеет следующий вид: <идентификатор> := <выражение>; Для идентификатора (имени переменной) допускается использовать любой тип, за исключением файлового. При этом тип идентификатора и тип выражения в операторе присваивания должны быть совместимы [1–3], т.е. для арифметического выражения используется переменная арифметического типа, для логического выражения – переменная логического типа и т.п. С помощью этого оператора переменной, идентификатор которой стоит в левой части, присваивается значение выражения. Для обозначения операции присваивания применяется составной символ присваивания ( := ), слева от которого записывается имя переменной, а справа выражение, значение которого предварительно вычисляется перед выполнением присваивания. Пример арифметического оператора присваивания, где переменным присваиваются значения арифметических выражений: y := x*y + sin(x); { VAR x, y: real ; } x := 0; { VAR x: integer ;} Пример логического оператора присваивания, где переменной присваивается значение логического выражения: B := ( X<0 ) OR ( K>1 ); { VAR X, K: real; B: boolean;} . Пример оператора присваивания, где переменной присваивается символ: S := ' + '; { VAR S: char;} 3.3. Процедуры ввода-вывода Ввод данных осуществляется с клавиатуры с помощью процедур Read или ReadLn. При повторных вызовах процедура Read позволяет вводить данные в одной и той же строке, а ReadLn выполняет ввод каждый раз с новой строки. Например, ReadLn(x); означает ввод одного значения для переменной х. При выполнении данной процедуры происходит приостановка выполнения действий в программе и переход компьютера в состояние ожидания. Для ввода данных необходимо при помощи клавиатуры набрать нужное значение для переменной х и затем нажать клавишу ввода “Enter”. Для процедуры ввода Read(x, y); необходимо будет ввести через пробел уже два значения: одно для переменной х, другое для переменной y. Вывод данных на экран монитора осуществляется при помощи процедур write или writeln. При повторных вызовах процедура write продолжает выводить данные в одной и той же строке, а writeln выводит данные каждый раз с новой строки. Например, процедура WriteLn(n:3); позволяет вывести на экран значение переменной n целого типа по заданному формату “ :3 ”. Согласно этому формату число позиций, отводимых под запись всего числа, включая его знак, будет равно 3. Процедура Write(‘ s = ’ , s:8:3); выводит на экран сначала комментарий в виде символов s =, а затем само значение вещественной переменной s по указанному формату “ :8:3”, где 8 будет задавать общее число позиций, отводимых под запись всего числа, включая его знак, а 3 определяет число цифр после десятичной точки в записи этого же числа. 3.4. Стандартные функции Pascal ABC В таблице 2 приведены стандартные функции языка Pascal ABC, которые можно использовать в программах. Таблица 2
Окончание табл. 2
3.5. Целые типы в Pascal ABC В Pascal ABC имеется три стандартных типа целых чисел: Byte, Integer и Word. Диапазон их возможных значений зависит от внутреннего представления числа, которое может занимать один, два или четыре байта. В таблице 3 приведены характеристики этих целых типов. Таблица 3 Классификация целых типов
MAXINT <= K <= MAXINT Описание переменных целых типов производится в разделе описаний VAR: Var <имя переменной> : <целый тип>; где <целый тип > может быть определен как Byte, Integer или Word. Например: VAR K: INTEGER; I, J: BYTE; Для целых типов определены следующие операции: сложение, вычитание (имеют более низкий приоритет), умножение и деление DIV, MOD. К целым типам применимы функции из таблицы 4. Функции TRUNC(X) и ROUND(X) с вещественным аргументом также дают целый результат (см. табл. 2). Стандартные математические функции в случае задания целого аргумента всегда возвращают вещественные значения (см. табл. 2). При использовании процедур и функций с целочисленными параметрами следует руководствоваться правилом «вложенности» типов, т.е. везде, где в качестве аргумента используется тип WORD, можно применять тип BYTE. Для арифметических операций, если операнды относятся к разным целым типам, тип результата имеет максимальную мощность диапазона, т.е. для типов операндов Byte и Word в выражении тип результата будет Word. Таблица 4 Встроенные процедуры и функции для целых типов
3.6. Вещественные типы В отличие от целых типов значения вещественных типов определяют число с десятичной точкой лишь с некоторой точностью, зависящей от внутреннего представления числа. Вещественное число в памяти ПК хранится в формате, состоящем из знака, мантиссы и порядка числа. Десятичная точка подразумевается стоящей перед левым (старшим) разрядом мантиссы (такая мантисса называется нормализованной). При выполнении операций десятичная точка сдвигается путем выполнения умножения мантиссы на E (символ экспоненты) с порядком. Например, запись числа в виде: <знак> <мантисса> Е <порядок> соответствует представлению числа <знак> <мантисса>*10 <порядок>. В Pascal ABC используются только два вещественных типа – REAL и COMPLEX , характеристики которых приведены в таблице 5. Таблица 5 Вещественные типы
Объявление переменных вещественных типов производится в разделе описаний переменных VAR аналогично переменным целых типов в виде: Var <переменная> : <вещественный тип>; где <вещественный тип > может быть задан только Real или Complex. Для работы с вещественными типами определены стандартные функции: sin, cos, arctаn, ln, exp, sqr, abs, sqrt (табл. 2), а также функции вещественного типа (табл. 6). Таблица 6 Встроенные функции вещественного типа
При этом операции +, -, *, / в арифметическом выражении дают вещественный результат, если хотя бы один из операндов вещественный. Переменные комплексного типа Данные комплексного типа (complex ) в программе записываются в скобках в виде (x,y), где x и y – выражения (константы, переменные) вещественного типа, представляющие собой вещественную и мнимую части комплексного числа. Если переменнаяc имеет тип complex, то обратиться к ее вещественной и мнимой частям можно как к полям записи: c.re и c.im. Например: const c1 = (0,1); var c: complex; ... c.re := 2*c.im; c := c1*c+(c.im, c.re); Для работы с переменными типа complex также используются стандартные функции: abs, sin, cos, exp, ln, sqrt . Кроме того применяется функция conj(C), возвращающая значение, комплексно сопряженное к C, и функция carg(C), возвращающая главное значение аргумента комплексного числа C, которое находится в числовом диапазоне (-Pi, Pi). 3.7. Примеры и задания к самостоятельному выполнению Ниже приводятся три простейшие программы линейной структуры, в которых используются оператор присваивания и процедуры ввода-вывода. Пример 1. Вычислить площадь прямоугольника по размерам сторон А и В. Обозначим площадь переменной S, тогда необходимо найти S = A*B. Программа набирается в окне редактора и исполняется клавишей [F9]: Program RECT ; {заголовок программы с именем RECT} const {заголовок раздела описания констант} A=2 ; B=3 ; {объявление констант А и В} var {заголовок раздела описания переменных} S: integer; {объявление переменной S целого типа} begin {начало основного блока программы} S := A*B; {оператор присваивания} write( ' Площадь прямоугольника = ' , S); {процедура вывода данных} end . {конец основного блока} В результате выполнения программы (Ctrl+F9) на экран выводится сообщение: Площадь прямоугольника = 6. П 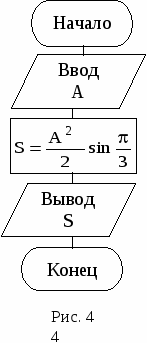 ример 2. Найти площадь равностороннего треугольника. ример 2. Найти площадь равностороннего треугольника.Если стороны треугольника имеют размер А, то его площадь S = A2 sin(π/3)/2. Схема алгоритма (СА) реализации этой задачи (рис. 4) выполнена по ГОСТ 19.701-90 (прил. 1). Текст программы: Program TREUG ; var A, S: real; begin writeln( ' Введите A ' ); {процедура вывода текста} read(A); {процедура ввода исходных данных} S: = SQR(A) * sin (PI / 3) / 2; writeln (' Результат: S= ' , S: 6: 2 , ' для A= ' , A); end . После выполнения программы на экран выводится сообщение Результат: S = 10.83 для А = 5. Предварительно рассчитанный на калькуляторе результат для А = 5 составил S = 10.8253, что подтверждает правильность работы программы. Пример 3. Вычислить функцию y сначала при х = 0 , а затем при х = 2: где A = 1.2, B = 0.5, C = 0.8 . Получаем следующий текст программы: Program Fun ; Const A = 2; B = 0.5; C = 0.8; var X : integer; // переменная X целого типа Y : real; // переменная Y вещественного типа Begin writeln( ' Введите Х ' ); {процедура вывода текста} read( X ); // введите значение переменной X Y := A*EXP(C*X) C*cos(B*X) +1; writeln( ' X= ' , X :3, ' Y= ' , Y:8:3); // вывод значений X и Y End. Задания к самостоятельному выполнению (программа_1_1) Вычислить значение некоторой функции, зависящей от констант a, b, c и переменной X, два значения x1 и x2 для которой заданы в таблице.
4. ПРОГРАММИРОВАНИЕ РАЗВЕТВЛЕННЫХ АЛГОРИТМОВ 4.1. Логические выражения Как известно, логическая константа может принимать только два значения: FALSE (ложь) и TRUE (истина). Переменные логического типа объявляются ключевым словом BOOLEAN в разделе описания переменных VAR и также могут принимать только два значения FALSE или TRUE (FALSE Для данных логического типа значению FALSE соответствует в компьютере число 0, значению TRUE – число 1, которые записываются в ячейку памяти длиной 1 байт [6, 7]. Для значений TRUE и FALSE справедливы следующие функции: ord (FALSE) = 0; ord (TRUE) = 1; succ (FALSE) = TRUE; pred (TRUE) = FALSE. Простым логическим выражением называется выражение, содержащее только логические операнды (константы или переменные типа Boolean). В сложных логических выражениях кроме логических операндов используются бинарные и/или унарные логические операции, а также стандартные функции (табл. 2) и операции отношений: <, <=, >, >=, =, <> . Операции отношения также относятся к операциям логического типа. Их можно использовать для проверки соотношений между переменными и константами типов real, integer, char, string. Например: a < b, x>=0, x=y и т.д. К бинарным операциям относятся логические операции: AND (логическое "И"), OR (логическое "ИЛИ"), XOR ("исключающее ИЛИ"), а к унарным операция NOT (отрицание "НЕ"). В логических выражениях без скобок согласно приоритету логических операций (см. табл. 1) сначала выполняется операция NOT, затем AND, после неё OR и XOR , а в последнюю очередь операции отношений. Логические операции используют понятия алгебры логики (булевой алгебры). Они применяются в задачах, когда нужно проверить какое-либо сложное условие. Операция конъюнкции and (логическое умножение) в логическом выражении AandB дает результат true (истина), если A и B имеют значение true, иначе во всех остальных случаях – false (ложь). Операция дизъюнкции or (логическое сложение) в логическом выражении AorB дает результат false, если A и B одновременно имеют значение false, во всех остальных случаях – true. Операция инверсии not (логическое отрицание) в логическом выражении notA дает результат true, если A = false и, наоборот, при A = true выражение not A примет значение false. Для переменных логического типа определена также операция присваивания. Пример: VAR С, D: REAL; X, Y, A, B: BOOLEAN; BEGIN X :=A OR B; Y := (C>0) AND (C END. Логический результат дает стандартная функция ODD(x) проверки на нечетность числа x, функции EOLN (f) проверки конца строки и EOF(f) определения конца файла f. 4.2. Условный оператор IF Условный оператор позволяет проверить некоторое условие и в зависимости от результата проверки этого условия выполнить то или иное действие, т.е. создать ветвление в программе. Структура условного оператора в полной форме имеет следующий вид: IF <условие> THEN <оператор1> ELSE <оператор2>; (если) (то) (иначе) где <условие> это выражение логического типа, которое может принимать только два значения: TRUE (истина) или FALSE (ложь). Правило выполнения условного оператора. Вначале вычисляется значение <условия>, стоящего за IF. Если результат условия истинен (TRUE), то выполняется только <оператор1>, а <оператор2> пропускается и выполняется следующий оператор. В противном случае выполняется <оператор2>, а <оператор1> пропускается и выполняется следующий оператор в программе. Структура условного оператора в сокращенной форме следующая: IF <условие> THEN <оператор1>; Здесь в случае ложности <условия>, стоящего за IF, пропускается <оператор1> и выполняется следующий за ним оператор программы. В качестве <оператор1> или <оператор2> по синтаксису может выполняться только один оператор Паскаля. Для выполнения после THEN или после ELSE неcкольких операторов применяется составной оператор с операторными скобками ( BEGIN … END ) . Несколько условных опеpатоpов могут быть вложены друг в друга. Ниже приведен пример вложения для трёх условных опеpатоpов: IF <условие1> THEN IF <условие2> THEN IF <условие3> THEN <оператор3> ELSE <оператор4> ELSE <оператор2> ELSE <оператор1>; 4.3. Составной и пустой операторы Составной оператор используется в том случае, когда по правилам синтаксиса сложного оператора должен стоять только один оператор, а в алгоритме необходимо выполнить некоторую последовательность действий. Составной оператор объединяет эту последовательность в единый по синтаксису оператор путем заключения в операторные скобки begin и end. Например: ВEGIN <оператор1>; <оператор2>; . . . ; <операторN> END; Для составного оператора допускается любая глубина вложенности: BEGIN BEGIN . . . BEGIN . . . END; . . . END; END ; Пустой оператор не выполняет никаких действий и может быть использован для передачи управления в конец составного оператора. Пустой оператор записывается в виде точки с запятой. Например, пустыми операторами будут следующие записи: 1) ; ; 2) <метка>: ; 4.4. Оператор безусловного перехода Оператор безусловного перехода позволяет изменить обычный последовательный порядок выполнения операторов и непосредственно перейти к нужному оператору, предварительно помеченному меткой. Структура такого оператора: GOTO <метка>; где GOTO ключевое слово, обозначающее перейти к <метке>, <метка> является произвольным идентификатором, который позволяет пометить любой оператор в программе и потом ссылаться на него. Оператор от метки отделяется двоеточием. В языке Pascal ABC допускается использовать в качестве метки также целое число без знака. Пример: LABEL m1, loop; VAR a, b, c, d: word; BEGIN m1: a := b+c*d; . . . goto m1; loop: END. Все использованные в программе метки должны быть описаны в разделе описаний программы с указанием ключевого слова “LABEL”. Описанные в этом операторе метки обязательно должны быть использованы в программе. Метки, описанные в функции или процедуре, локализуются только в ней, передача управления извне процедуры на метку внутри ее невозможна. С помощью оператора GOTO не рекомендуется осуществлять переход во внутреннюю часть сложного оператора (цикла, составного оператора). Запрещается переход с одной альтернативной части (ветви) сложного оператора на другую. Современная технология структурного программирования основана на принципе программирования без GOTO. Считается, что злоупотребление этими операторами затрудняет чтение программы, усложняет ее отладку. Тем не менее, в некоторых случаях использование оператора перехода может упростить программу. Обычно GOTO используется для досрочного выхода из любого сложного оператора или вложенных операторов цикла. 4.5. Пример и задания с оператором IF Пример. Вычислить значения функции y(x) в зависимости от интервала, в который попадает аргумент x.  Для x [-10,5] Для x [-10,5] где а = 1.5, b = 0.5 ; Напишем программу, соответствующую схеме алгоритма (рис. 5): Program Lr2; Label m1, 10; Const A = 1.5; B = 0.5; var x, y: real; // переменные вещественного типа Begin m1: read(x); // вводим значение переменной x IF (x < -10) or (x>5) then goto m1; IF x<0 then begin y:= a*x+b ; goto 10 end ; if (x >= 0) and (x<=2) then y :=A*SQR(x)*LN(x+1) ; if x>2 then y := EXP(A*x+1)*COS(B*x); 10: writeln( ' x= ', x :8:1 , ' y= ' , y :8:2); //вывод значений x и y End. К Да Да Нет Нет Да     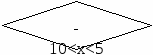 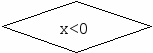 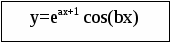   | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||