Учебное пособие Омск Издательство Омгту 2010 удк 004. 4 (075) ббк 32. 973018я73 ч 49 Рецензенты

• Название: Учебное пособие Омск Издательство Омгту 2010 удк 004. 4 (075) ббк 32. 973018я73 ч 49 Рецензенты
• Анкор: ABC_Pascal.doc
• Дата: 15.02.2017
• Размер: 1.07 Mb.
• Имя файла: ABC_Pascal.doc
• Тип: Учебное пособие; #2721
• страница: 4 из 8

Const n = 14;

a = 0.6*Pi;

b = 0.7*Pi;

Var x, y1, y2, dx: real;

Begin

dx:=abs((a-b)/n);

x:=a;

Repeat

y1:=sin(x)/cos(x);

y2:=1/y1;

writeln('x=', x:6:4,' y1= ', y1:7:4,' y2=', y2:7:4);

x:=x+dx

Until x>b;

End.

Пример 2. Вычислить сумму s = 1+1/4+1/9+1/16 +...

с 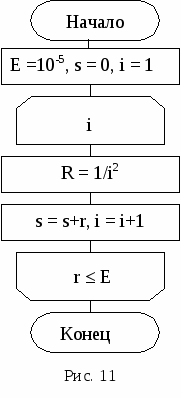точностью до E = 0.00001 (рис. 11).

PROGRAM summa;

CONST

E = 0.00001; {точность}

VAR

s, r: REAL; { s – сумма, r – слагаемое}

i: INTEGER; { i – счетчик слагаемых}

BEGIN

s:=0;

i:=1;

REPEAT

r: = 1/sqr(i); {вычисление слагаемого}

s := s + r;

I := I + 1 {счет слагаемых}

UNTIL r
WRITELN ( 'Сумма = ' , s:9:5); {вывод суммы}

END.
Задания для самостоятельного выполнения

Задание 1 (программа_5_1)

Модифицировать программу 3_2 для вычис­ления функций F1(x) и F2 (x) с применением опе­ратора цикла с постусловием. Выполнить ее и сравнить результаты с полученными ранее.
Задание 2 (программа_5_2)

Начертить структурную схему алгоритма, написать и отладить прог­рамму для одной из следующих задач.

1. Вычислить приближенное значение z = arctg x и сравнить с

x - x³/3 + x⁵/5 - ... + (-1)ⁿx²ⁿ⁺¹/(2n+1) + ... (|х|<1), прекращая вычисления, когда очередной член по абсолютной величине бу­дет меньше eps = 0.00001.

2. Вычислить y = x - x²/2 + x³/3 - ... + (-1)^n-1xⁿ/n ^{+ ...} с точностью eps = 0.00001,

где |x|<1. Сравнить результат с вычисленным через стандартную функцию значением y = LN(1+x).

3. Вычислить y = 1 + x/1! + x²/2! + ... + xⁿ/n! + ... с точностью eps = 0.00001 и сравнить результат с вычисленным через стандартную функцию значением
y = ЕXP(x).

4. Вычислить y = sin x = x - x³/3! +x⁵/5! -...+ (-1)ⁿx²ⁿ⁺¹/(2n+1)!+... с точностью eps = 0.00001.

5. Вычислить y = 1 - x²/2! + x⁴/4! - ... + (-1)ⁿx²ⁿ/(2n)! + ... с точностью
eps = 0.0001 и сравнить результат с вычисленным через стандартную функцию значением y = cos (x).

6. Найти произведение цифр заданного натурального числа.

7. Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа.

8. Определить номер первого из чисел sin x, sin(sin x), sin(sin(sin x)), ... , меньшего по модулю 10^-3.

9. Дана непустая последовательность различных целых чисел, за которой следует нуль. Определить порядковый номер и величину наиболь­шего среди отрицательных чисел этой последовательности.

10. Вычислять периметры и площади прямоугольных треугольников по длинам катетов, пока один из заданных катетов не окажется нулевым.

11. Дана непустая последовательность положительных целых чисел, за которой следует отрицательное число (это признак конца последова­тельности). Вычислить среднее геометрическое этих чисел.

12. Дана непустая последовательность ненулевых целых чисел, за которой следует нуль. Определить, сколько раз в этой последователь­ности меняется знак.

13. Числа Фибоначчи (f_n) определяются формулами

f₀ = f₁ = 1_; f _n = f _n-1 + f _n-2 при n = 2,3,... .

Вычислить сумму всех чисел Фибоначчи, которые не превосходят 1000.

14. Дана непустая последовательность положительных вещественных чисел х₁, х₂, х₃,..., за которыми следует отрицательное число. Вычис­лить величину
х₁ + 2х₂ + ... + (N-1)x_N-1 + N х_N, где N заранее не известно.

15. Вычислить длины окружностей, площади кругов и объемы шаров для ряда заданных радиусов. Признаком окончания счета является нулевое значение радиуса.

16. Определить, есть ли среди цифр заданного числа одинаковые цифры.

17. Определить, является ли заданное натуральное число палиндромом, т. е. таким, десятичная запись которого читается одинаково слева направо и справа налево.

18. Вычислить наименьшее общее кратное натуральных чисел a и b.

19. Дано число L. Определить первый отрицательный член последовательности х₁, х₂, х₃,..., где х₁ = L, x_i = tg(x_i-1).

20. Определить, является ли заданное натуральное число совершенным, т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, совершенное число 6 = 1 + 2 + 3).

6. СТРУКТУРИРОВАННЫЕ ТИПЫ ДАННЫХ
6.1. Массивы данных

Массивы – упорядоченная структура однотипных данных, хранящихся в памяти последовательно. Массив обязательно имеет размеры. Описывается в разделе TYPE или VAR следующим образом:

Type <имя_типа> = array [диапазон_индексов] of <базовый_тип>;

или

Var <имя_переменной> : array [ диапазон_индексов] of <базовый_тип>;

Отметим, что в разделе Type разделителем служит символ “=”, а в разделе переменных var – двоеточие “ : ” .

Пpимер: TYPE

array10 = array [1..10] of integer;

array11 = array [11..22] of real;

VAR

V: array[-3..2] of char; {массив из 6 элементов}.

В качестве индексов можно использовать любые перечислимые типы как встроенные, так и вводимые программистом. Индексы могут задаваться также диапазоном. Если диапазон соответствует всему типу, можно просто указывать имя этого типа.

Например:

TYPE DIAP = 1..100;

VECTOR = array [DIAP] of real;

При записи сложных массивов индексы разных диапазонов могут при­надлежать разным типам. Например:

VAR V: array [0..10 , 'A'..'C' ] of real;

В качестве значений диапазона могут использоваться идентификато­ры, если их значения определены выше. Например:

CONST

K=10; L=5;

VAR

A: ARRAY [1..K] OF INTEGER;

B,С: ARRAY[1..K,1..L] OF REAL;

Массивы хранятся в памяти как сплошные последовательности компо­нентов, причем быстрее изменяется дальний правый индекс.

Обращение к элементу массива в программе производится указанием имени массива и индексов, заключенных в квадратные скобки:

<имя> [ <индексы> ].

Пример:

A[1] := 1; B[8,5] := В[8,1] + B[8,2]; V[1,'B'] := 3.5; .

В данном типе определена единственная операция присваивания. Мож­но присваивать целиком весь массив лишь массиву того же типа и размерности, например: B := С.

Операции сравнения в массивах производятся только поэлементно.

Обнуление одновременно всех элементов массива выполняется в цикле

FOR I :=1 TO K DO A[I] := 0.

Разрешается объявлять массивы, где базовыми элементами служат также массивы, например:

TYPE

VECTOR = array[1..5] of real;

MATRIX = array[1..10] of VECTOR;

что эквивалентно следующему способу описания:

MATRIX = array[1..10] of array[1..5] of real;

или

MATRIX=array[1..10, 1..5] of real;
Типизированные константы-массивы

В качестве типизированных констант можно использовать массивы. В константах-массивах список констант разделяется запятыми и зак­лючается в круглые скобки:

CONST vector : array[0 .. 4] of byte = ( 0, 1, 2, 3, 4 );

массив символов может быть описан следующей записью:

CONST vec : array[-1..2] of char = ( 'a' , 'b' , 'c' , 'd' );

При объявлении многомерных констант-массивов список констант, соответствующих каждому измерению, заключается в дополнительные круглые скобки и отделяется от соседних списков запятыми. Самый внутренний список констант связывается с изменением самого правого индекса масси­ва. Например:

CONST

matr: array[1..2, 1..4] of byte = ((0,1,2,3),(4,5,6,7));

cub: array[0..1, 1..2,1..3] of byte = (((0,1,2),(3,4,5)),

((6,7,8),(9,10,11)));

6.2. Пример и задания для одномерных массивов

Пример. Найти значение и номер наименьшего элемента в одномерном массиве. При задании элементов исходного массива типизированной константой СА решения задачи имеет вид (рис. 12, а) и используется следующая программа:

Program lr6_1;

const

a: array[1..10] of integer = (5,2,7,1,8,3,4,5,6,6);

var

i, min, n: integer;

begin

min:=a[1];

n:=1;

for i:=2 to 10 do

if a[i]
min:=a[i];

n:=i

end;

writeln('минимальный элемент равен ',min, ' n=',n);

end.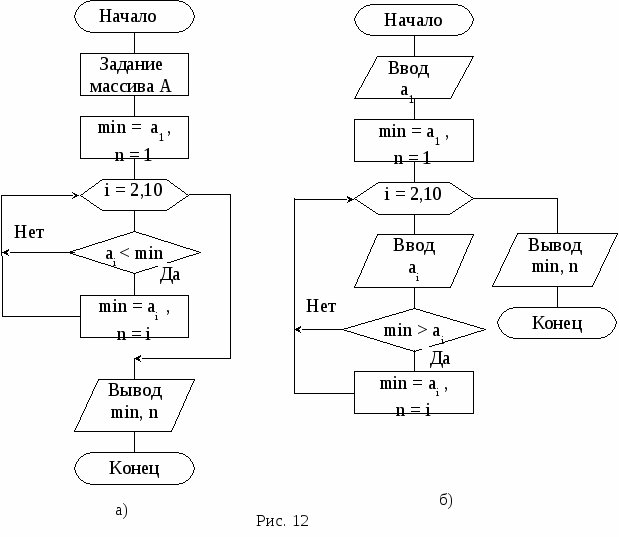



Если элементы массива вводятся с клавиатуры, то СА имеет вид (рис. 12, б) и текст программы изменится:

program lr6_2;

var a: array[1..10] of integer;

i, min, n: integer;

begin

read(a[1]);

min:=a[1]; n:=1;

for i:=2 to 10 do begin

read(a[i]);

if a[i]
min:=a[i]; n:=i;

end;

end;

writeln('минимальный элемент равен ', min, ' n=',n);

end.
Задания для самостоятельного выполнения

Задание 1

Начертить структурную схему алгоритма, написать и отладить прог­рамму для одной из следующих задач. В одной программе исходные массивы задать типизированными константами. В другой программе элементы исходных массивов ввести через оператор ввода.

1. Дан массив из N чисел (N > 8). Вычислить их среднее геомет­рическое значение.

2. Дан массив из N чисел (N > 10). Найти максимальное значение.

3. Дано 20 чисел. Найти их среднее арифметическое значение.

4. Дано 12 вещественных чисел. Найти порядковый номер того из них, которое наиболее близко к какому-нибудь заданному целому числу Х.

5. Дана последовательность из 15 целых чисел. Определить коли­чество отрицательных чисел в ней и максимальное число подряд следую­щих отрицательных чисел.

6. Дано 15 целых чисел. Найти наибольшее из них. Определить, сколько из чисел принимает наибольшее значение.

7. Дано целое n > 1 и вещественные числа x₁, x₂, .., x_n. Вычислить математическое ожидание и дисперсию по формулам:

M =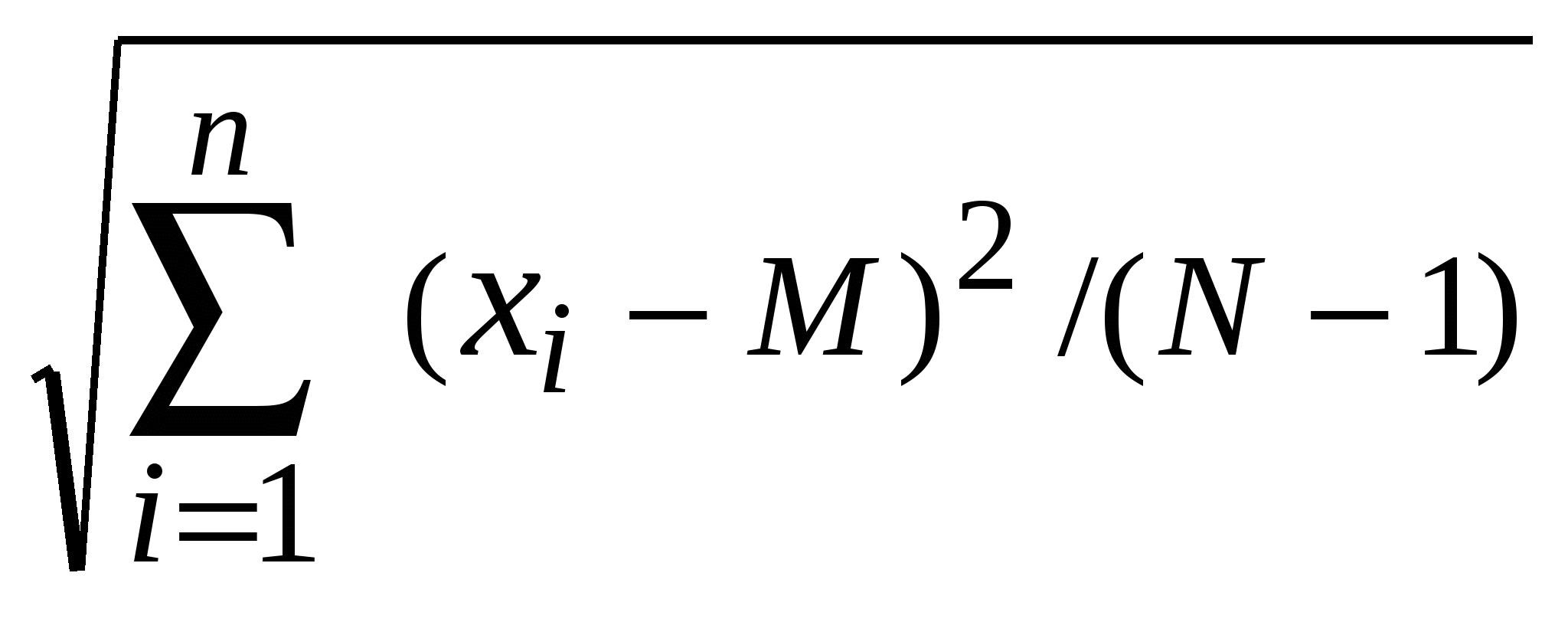, D =.

8. Дан массив из N чисел (N > 10). Вычислить сумму элементов с нечетными индексами и их среднее арифметическое значение.

9. Даны два одномерных массива А и В. Вычислить элементы массива С по правилу: если а_i и b_i различны, то с_i присвоить их сумму, при одинаковых а_i, b_i в с_i переписать соответствующий элемент массива А.

10. Дано 10 вещественных чисел. Вычислить разность между максимальным и минимальным из них.

11. Дано 10 вещественных чисел. Определить, образуют ли они воз­растающую последовательность.

12. Дан массив X из n чисел (n >10). Вычислить:

y = x₁ - x₂ + x₃ - ...- x_n-1 +x_n .

13. Дано 18 чисел. Определить количество элементов, отличное от послед­него числа.

14. Дано 12 чисел. Напечатать сначала все отрицательные из них, а затем все остальные.

15. Сформировать одномерный массив из 15 простых чисел.

16. Дано восемь натуральных чисел. Найти их наибольший общий де­литель.

17. Дана последовательность натуральных чисел. Вычислить сумму тех из них, порядковые номера (индексы) которых – простые числа.

18. Дан массив из 20 натуральных чисел. Вычислить сумму тех из них, порядковые номера которых - числа Фибоначчи, определяемые форму­лами

f₀ = f₁ = 1; f_n = f_n-1 + f_n-2 при n = 1, 2, 3, ... .

19. Дан массив X из n чисел. Вычислить:

y = x_n(x_n+x_n-1)(x_n + x_n-1 + x_n-2)...(x_n + ... + x₁) .

20. Дано 24 целых числа. Распечатать их в обратном порядке по шесть чисел в строке.

Задание 2

Модифицировать программу_3_2 для функций F1(x) и F2 (x) таким образом, чтобы результаты были сформированы в виде трех одномерных массивов. Выполнить ее и сравнить результаты с полученными в программах_5_1_и_3_2.
6.3. Ограниченный тип (диапазон)

Через диапазон можно определить тип, который будет содержать зна­чения только из ограниченного поддиапазона некоторого базового типа. Базовым типом может быть любой целочисленный тип, тип CHAR или любой из введенных программистом перечислимых типов. Определяется тип-диапазон в разделе TYPE указанием имени типа и границ диапазона, разделенных двумя точками:

TYPE <ИмяДиапазона> = < НачальноеЗначение> . . <КонечноеЗначение>;

Начальное значение при определении такого типа не должно быть больше конечного.

Пример: TYPE

TEST1 = (test1, test2, . . . ,test5 );

H= 1.. 20; {поддиапазон для типа Integer}

LETERS = 'A' .. 'Я'; {базовый тип Char}

TESTOD = test2 .. test5; {базовый тип TEST1}

Определение переменных для диапазона производится в разделе VAR. Они могут принимать любые значения из указанного диапазона, включая граничные.

При конструировании диапазона в описании типа можно использовать несложные арифметические выражения для вычисления границ. Но при этом надо следить, чтобы запись выражения не начиналась со скобки (скобка  это признак начала перечисления).

Пример:

CONST N = 30;

TYPE date = 1..31;

kv2 = 3*N+1..6*N;

VAR L, L1: date;

k: kv2;

BEGIN

L:=2*10+5; ...

L1:=2*10+60; {неверно, т.к. L1 выходит за пределы диапазона}

END.

Применение ограниченных типов усиливает контроль данных при вы­полнении программы. Значения переменных типа «диапазон» могут выводить­ся на экран и вводиться с клавиатуры только в том случае, когда диапа­зон взят из базового стандартного типа.

6.4. Пример и задания для двумерных массивов

Пример. Вычислить суммы элементов в столбцах двумерного числового массива А размером [1..3,1..4].

Текст программы для СА (рис. 13):

P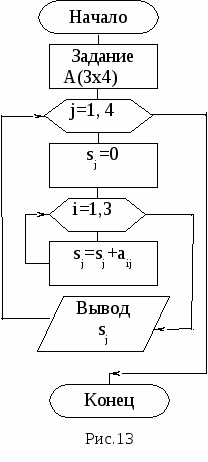rogram lr7_1;

CONST a: array[1..3,1..4] of integer =

((1,2,3,4),(1,2,3,4),(1,2,3,4));

VAR

i, j: integer;

s: array[1..4] of integer; {массив сумм}

BEGIN

for j := 1 to 4 do

begin

s[j] := 0;

for I := 1 to 3 do

s[j] := s[j] + a[i,j];

write(' s[' , j, ']=' , s[j])

end

END.


Задания для самостоятельного выполнения

Задание 1

1. Даны матрицы A,B: array [1..4,1..4] of real. Вычислить матрицу С поэлементным сложением соответствующих элементов матриц А и В.

2. Дана матрица B: array [1..5,1..5] of real. Найти для нее транспонированную.

3. Даны матрица A: array[1..4,1..4], содержащая вещественные числа, и константа k. Вычис­лить матрицу С = k*А .

4. Сформировать массив по правилу 1 0 0 ... 0

2 1 0 ... 0

3 2 1 ... 0

...

10 9 8 ... 1

5. Даны натуральное N и элементы а_ij квадратной вещественной матрицы А пятого порядка. Вычислить N-ю степень каждого элемента этой матрицы по схеме (а_ij¹ = а_ij, а_ij² = а_ij*а_ij, а_ij³ = а_ij²*а_ij и т.д., где i, j = 1, 2, ..., 5).

6. Сформировать массив по правилу 0 0 0 ...0

0 1 0 ...0

0 0 2 ...0 .

…

0 0 0 ...9

7. Сформировать массив последовательностью натуральных чисел:

1 2 ... 10

11 12 ... 20

21 22 ... 30 .

...

91 92 ... 100

8. Сформировать двумерный массив: 1 2 3 4 5

5 1 2 3 4

4 5 1 2 3 .

3 4 5 1 2

2 3 4 5 1

9. Дана матрица A: array [1..N,1..N] of integer. Сформировать век­тор В из максимальных элементов каждой строки.

10. Дана матрица A: array [1..6,1..6] of integer и переменная x. Элементы нечетных строк матрицы А заменить на значение x.

11. Дана матрица B: array [1..5,1..5]. Получить массив С удалением (либо обнулением) n-й строки и k-го столбца из матрицы В.

12. Определить, является ли заданная квадратная матрица девятого порядка магическим квадратом, т.е. такой, в которой суммы элементов во всех строках и столбцах будут одинаковы.

13. Определить, является ли заданная целая квадратная матрица шестого порядка симметричной (относительно главной диагонали).

14. Дана вещественная матрица A: array [1..7,1..4]. Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент оказался в верхнем левом углу.

15. Дана вещественная матрица размером 4х8. Упорядочить ее стро­ки по не- убыванию сумм их элементов.

16. Для заданной целой матрицы размером 6х8 элементов напечатать индексы всех ее седловых точек. Элемент матрицы называется седловой точкой, если он является наименьшим в своей строке и одновременно на­ибольшим в своем столбце или, наоборот, является наибольшим в своей строке и наименьшим в своем столбце.

17. Дана матрица A: array [1..6,1..2] вещественных чисел. Рассмат­ривая A [i,1] и A [i,2] как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь кото­рого попадают все эти точки.

18. Дан массив F: array [1..N,1..M] of byte. Определить количество «особых» элементов в нем. Элемент считается «особым», если он больше суммы остальных элементов своего столбца.

19. Дана матрица D: array [1..5,1..6] of integer. Упорядочить эле­менты строк в нем по убыванию.

20. Дан массив М координат точек на плоскости. Найти наибольшее расстояние между этими точками.
Задание 2

Сформировать таблицу Пифагора для чисел натурального ряда.

Задание 3

Модифицировать программу_3_2 (или 6_3) таким образом, чтобы значения X, F1 и F2 были представлены двумерным массивом, состоящим из трех строк.

7. СТРУКТУРНОЕ ПРОГРАММИРОВАНИЕ
7.1. Структура сложной программы

Любая программная единица включает следующие разделы:

<Объявление программной единицы>

{Раздел описаний}

BEGIN

{Раздел исполняемых операторов}

END. {символ конца программной единицы}

<Объявление программной единицы>  заголовок программы, процедуры или функции. Заголовок программы можно опускать, для процедур и функ­ций наличие заголовка обязательно.

 это символ точки для прог­раммы или символ ";" для процедуры или функции.

В разделе описаний объявляются идентификаторы типов, объектов, констант, переменных, а также метки, процедуры и функции. Каждый блок определяется своим ключевым словом. Тогда структура программы будет иметь вид

PROGRAM <имя программы>;

USES <список библиотечных модулей>;

LABEL <список меток в основном блоке>;

CONST < определение констант>;

TYPE <определение типов>;

VAR <определение глобальных переменных>;

<определение процедур>

<определение функций>;

BEGIN

<основной блок программы>

END.

Директива USES выполняет подключение стандартных или написанных программистом модулей. Она должна обязательно стоять первой, если присутствует в программе. Например, строкой

USES CRT;

производится подключение модуля CRT. Модуль CRT содержит процедуры и функции для управления выводом текста на дисплей, звуковым генератором и чтением с клавиатуры.

БлокиTYPE, CONST, VAR, LABEL в Паскале АВС могут следовать друг за другом в любом порядке и встре­чаться в разделе описаний сколько угодно раз.

В блоке LABEL перечисляются через запятую метки, используемые в программной единице. Метка может содержать числовое значение либо являться идентификатором. Например: