Учебное пособие по дисциплине Разработка языков программирования высокого уровня
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
6.2 Основные понятия формы Бекуса-Наура (БНФ)Определение. Язык программирования - это множество последовательностей символов некоторого алфавита, удовлетворяющих правилам синтаксиса и задающих последовательность вычислений в соответствии с правилами семантики. Далее приведена интерпретация понятий КС-грамматики для языка программирования. Алфавит ЯП- набор символов, включающий в себя буквы, цифры, специальные символы и лексемы. Лексема- синтаксическая единица нижнего уровня, имеющая смысл. Для языка программирования лексемами являются идентификаторы, ключевые слова, знаки операций и т.п. Ключевые слова- множество зарезервированных в языке слов, определяют семантические понятия языковых конструкций или их частей. Идентификаторы- символические имена, которыми именуются объекты программы. Помимо синтаксической лексемы грамматика БНФ оперирует термином «грамматическая лексема», которая определяет смысл лексемы синтаксической, например, для Или объектов переменной длинны описываются в БНФ следующим образом: 1)Рекурсивными правилами, т.е. правилами, в которых левая часть входит в правую: <список идентификаторов>  <идентификатор>|<идентификатор>,<список идентификаторов>; <идентификатор>|<идентификатор>,<список идентификаторов>;2) фигурными скобками, которые указывают на то, что заключенная в них часть, может повторяться неограниченное количество раз или отсутствовать: <список идентификаторов>  <идентификатор>{идентификатор}; <идентификатор>{идентификатор};Квадратными скобками обозначается необязательная часть правой части цепочки символов (оператора языка): If<логическое выражение>then<оператор>[else<оператор>]; Круглыми скобками обозначают выбор из группы одного элемента: For<переменная>:=<выражение>(to|downto)<выражение>do<оператор>; Так же как и в КС-грамматике, в БНФ используются нетерминалы, которые определяют типы тех или иных операторов ЯПВУ. Например, оператор присваивания в терминалах множества переменных V в БНФ представляется переменными <присвоить> и <выражение> следующим образом: <присвоить>:=<выражение>; Пример 1. Пусть требуется описать грамматику для представления языка программирования, на котором можно писать программы с тремя переменными А,В,С, операторами присваивания “:=”, арифметическими выражениями со знаками операций “+”,”-” и ключевыми словами begin,end. Грамматика представляется следующим образом: Т={A,B,C,:=,+,-, ; , begin, end} V={<программа>, <оператор>, <список операторов>, <переменная>, <выражение>} S={<программа>} P: <программа>  begin begin <список операторов>end <список операторов>end<список_операторов>  <оператор>|<оператор>; <оператор>|<оператор>;<список операторов> <оператор>  <переменная>:=<выражение> <переменная>:=<выражение><переменная>  A|B|C A|B|C<выражение>  <переменная>+<переменная> <переменная>+<переменная>|<переменная>-<переменная> |<переменная> Пример порождения в описанной грамматике: <программа>=>begin<список_операторов>end =>begin|<оператор>;<список_операторов>end =>begin<переменная>:=<выражение>;<список_операторов>end =>begin A:=<выражение>;<список_операторов> end =>begin A:=<переменная>+<переменная>; <список_операторов> end =>begin A:=B + <переменная>;<список_операторов>end =>begin A:= B + C ;<оператор> end =>begin A:= B + C ; <переменная> :=<выражение>end =>begin A:= B + C ; B:=<выражение>end =>begin A:= B + C ; B:=<переменная>end =>begin A:= B + C ; B:=C end Каждая строка вывода называется сентенциальной формой. Здесь реализован левосторонний порядок вывода (левое порождение), т.е. подстановка формул осуществлялась слева (может быть и правосторонний вывод). Сентенциальная форма, в которой присутствуют только лексемы и терминалы называется порожденным предложением. 6.3 Синтаксические деревьяПорождения можно представить в виде синтаксического дерева или дерева разбора, которое показывает, как группируются символы (терминалы) вы цепочки языка. Определение. Синтаксическое дерево - это графическое представление порождения в виде иерархического списка, в котором: 1. Корень дерева - это стартовый символ грамматики - S 2. Узлы (вершины) дерева могут быть либо внутренними, т.е. являться переменными, принадлежащими множеству V, либо конечными - терминалами, которые принадлежат множеству T. При этом внутренние узлы всегда имеют наследников, конечные называют листьями дерева и потомков не имеют. 3. Если внутренний узел помечен переменной AєV, а ее наследники отмечены листьями х1,х2,...,хn, то А является продукцией, порождающей цепочка х1,х2,...,хn ( А → х1,х2,...,хn, причем х1,х2,...,хn выписаны слева направо по дереву. Пример 2. Пусть дана грамматика: <присвоить> → <идентификатор> + <выражение> | <идентификатор> * <выражение> | (< выражение >) |<идентификатор >| Эта грамматика описывает оператор присваивания с операциями "+","-" и круглыми скобками. Например, оператор А := В * ( А + С ) порождается следующим выводом <присвоить> => <идентификатор> := <выражение> => А := <выражение> => А := <идентификатор> * <выражение> => А := В * <выражение> => А := В * ( <выражение> ) => А := В * (< идентификатор > + <выражение> ) => А := В * ( А + <выражение> ) => А := В * ( А + < идентификатор > ) => А := В * ( А + С ) 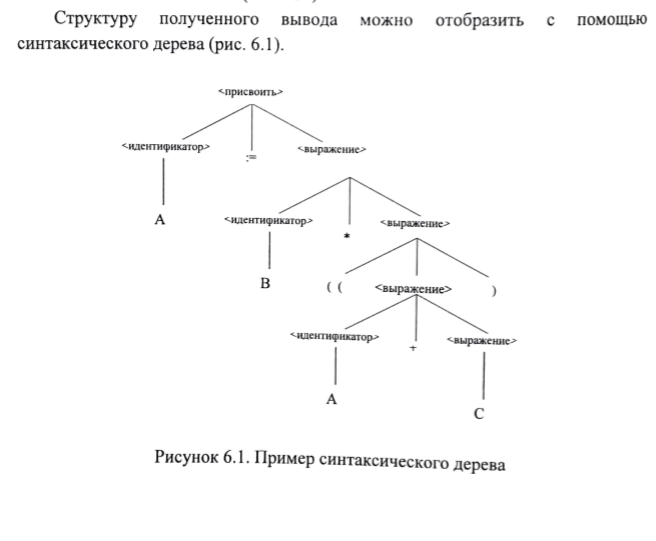 Рисунок 6.1 Пример синтаксического дерева Определение. Цепочка, выведенная из корня и выписанная слева направо из отметок листьев, называется кроной дерева. Утверждение 1. Терминальная цепочка принадлежит языку грамматики тогда и только тогда, когда она является кроной, по крайней мере, хотя бы одного дерева разбора. Это утверждение говорит о том, что существование порождений и синтаксических деревьев являются равносильными понятиями. Деревья задают порядок вычислений в арифметическом выражении, т.е. определяют приоритеты операций: чем ниже на дереве располагается знак операции, тем раньше она выполняется. 6.4. Неоднозначность грамматики выражений Утверждение 2. Для некоторых грамматик можно найти терминальные цепочки с несколькими деревьями разбора (рис. 5.6) или с несколькими левыми или правыми порождениями. Такие грамматики являются неоднозначными. Пример 3. Пусть задана грамматика оператора присваивания: <присвоить>→<идентификатор>:=<выражение> <идентификатор>→A|B|C <выражение>→<выражение>+<выражение> |<выражение>*<выражение> |(<выражение>) |<идентификатор> Эта грамматика неоднозначна, т.к. вывод цепочки А:=В+С*А можно представить двумя деревьями (рис. 6.2): Причины неоднозначности грамматики выражений заключается в следующем: 1. В грамматике не учтены приоритеты арифметических операций. 2. Не определен порядок выбора правил из множества Р при выводе выражения. Устранение неоднозначности состоит во введении в грамматику дополнительных переменных: a. множителей (сомножителей или факторов), b. слагаемых (термов) Множитель — это выражение, которое не может быть разделено на части никакой примыкающей операцией, ни "*", ни "+". Множителями для нашей грамматики могут быть: -идентификаторы, -выражения в скобках. Терм-это выражение, которое не может быть разорвано операцией “+”. Для нас терм-это произведение нескольких факторов F*F…. Тогда выражение- это любое возможное выражение, которое представляет сумму одного или нескольких термов.  Рисунок 6.2 Синтаксические деревья к выводу цепочки A:=B+C*A в неоднозначной грамматике Рисунок 6.2 Синтаксические деревья к выводу цепочки A:=B+C*A в неоднозначной грамматикеСТРАНИЦЫ 86-95 - идентификаторы, - выражения в скобках, Терм- это выражение, которое не может быть разорвано операцией “+”. Для нас терм- это произведение нескольких факторов F*F*… Тогда выражение- это любое возможное выражение, которое представляет сумму одного или нескольких термов.    <присвоить> <присвоить>    <идентификатор> := <выражение> <идентификатор> := <выражение>А     <выражение> <+> <выражение> <выражение> <+> <выражение>    <идентификатор> <выражение> <*> <выражение> <идентификатор> <выражение> <*> <выражение>  B <идентификатор> <идентификатор> B <идентификатор> <идентификатор>A C    <присвоить> <присвоить>    <идентификатор> := <выражение> <идентификатор> := <выражение>А     <выражение> <*> <выражение> <выражение> <*> <выражение>    <идентификатор> <выражение> <+> <выражение> <идентификатор> <выражение> <+> <выражение>  B <идентификатор> <идентификатор> B <идентификатор> <идентификатор>С А Синтаксические деревья к выводу цепочки А:=B+C*A в неоднозначной грамматике. Пример 4 Однозначная грамматика для вывода того же оператора присваивания А:=B+C*A, в которой учтён привычный приоритет арифметических операций, представляется следующим образом: <присвоить>  <идентификатор> <идентификатор> <выражение> <выражение>< идентификатор > A | B | C <выражение> < выражение > + <терм > | <терм > <терм > <терм > * < множитель > | < множитель > < множитель > (< выражение > ) | < идентификатор > Вывод предложения А:= В + С*А и однозначное дерево (рис.5.7). <присвоить> => < идентификатор > := <выражение> => А := <выражение> => А := <выражение> + < терм > => А := < терм > + < терм > => А := < множитель > + < терм > => А := < идентификатор > + < терм > => А := В + < терм > => А := В + < терм > * < множитель > => А := В + < идентификатор > * < множитель > ) => А := В + С * < множитель > ) => А := В + С * < идентификатор > ) => А := В + С * А Синтаксическое дерево изображено на рисунке 6.3.    <присвоить> <присвоить>    <идентификатор> := <выражение> <идентификатор> := <выражение>А     <выражение> <+> <терм> <выражение> <+> <терм>    <терм> <терм> <*> <множитель> <терм> <терм> <*> <множитель>   <множитель> <множитель> <идентификатор> <множитель> <множитель> <идентификатор> <идентификатор> <идентификатор>B <идентификатор> А С Рисунок 6.3. Синтаксическое дерево к порождению цепочки А:= В+С*А в однозначной грамматике Контрольные вопросы: 1.Определение КС-грамматики 2.Определение языка, заданного КС-грамматикой 3.Что такое форма Бэкуса-Наура? 4.Привести примеры грамматики для вывода арифметического выражения, оператора присваивания. 5.Сделать вывод оператора присваивания, в грамматике, определенной в п.5 6.Определение синтаксического дерева. 7.Что такое крона синтаксического дерева? 8.В чем заключается проблема неоднозначности грамматики арифметических выражений? 9.Как решается проблема неоднозначности грамматики арифметических выражений? ГЛАВА 7. ПОНЯТИЕ ОБ АКСИОМАТИЧЕСКОЙ СЕМАНТИКЕ ЯЗЫКА ПРОГРАММИРОВАНИЯ 7.1 Аксиоматическое описание программы. Основная теорема Семантика ЯПВУ- правила и условия, определяющие соотношения между элементами языка и их смысловыми значениями. Эти правила используются при доказательстве правильности программного обеспечения. Существует несколько способов формулировать эти правила. Одним из них является аксиоматическая семантика, разработанная Хоаром. Каждая программа имеет статическую и динамическую структуры. Статическая структура представляется ее текстом на языке программирования. Она не зависит от исходных данных. Динамическая структура: а) отражает процесс вычислений, поэтому зависит от исходных данных, т.к. именно их значения определяют передачи управления в программе при выполнении. б) состоит из последовательности состояний вычислений, которая зависит от исходных данных, т.к. их значения определяют передачи управления при вычислении. Состояние вычислений в каждый момент времени включает значения всех переменных в этот момент, которые зависят от предыдущих этапов вычислений. Состояние вычислений, таким образом, это слепки памяти в каждый момент времени. Текущий оператор изменяет состояние вычислений и передаёт управление другому оператору. Таким образом, каждый оператор (или программа) 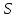 рассматривается как конструкция с одним входом и одним выходом ( рассматривается как конструкция с одним входом и одним выходом (рис.7.1).  S Исходное состояние вычислений 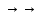 Выходное сост. вычислений Выходное сост. вычисленийРисунок 7.1. Представление оператора S Входы и выходы описываются логическими выражениями (предикатами), которые определяют состояния вычислений. Пусть  и и 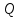 предикаты, описывающие вход и выход состояния вычислений, т.е. описывают ограничения, наложенные на значения переменных перед и после выполнения оператора (или программы); предикаты, описывающие вход и выход состояния вычислений, т.е. описывают ограничения, наложенные на значения переменных перед и после выполнения оператора (или программы); 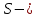 любой оператор (или программа). Тогда существует следующая теорема. любой оператор (или программа). Тогда существует следующая теорема.Основная теорема. Если некоторое логическое условие  истинно непосредственно перед выполнением S, то после выполнения S будет истинным некоторое в общем случае другое условие Q. истинно непосредственно перед выполнением S, то после выполнения S будет истинным некоторое в общем случае другое условие Q.Таким образом, если из истинности предиката  непосредственно перед выполнением S следует истинность условия Q после выполнения этого оператора, то говорят, что непосредственно перед выполнением S следует истинность условия Q после выполнения этого оператора, то говорят, что  есть предусловие для постусловия Q по отношению к оператору есть предусловие для постусловия Q по отношению к оператору 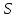 , т.е. сформулировано аксиоматическое описание S , т.е. сформулировано аксиоматическое описание S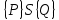 . .Утверждения. Для любых S и  всегда найдётся некоторый предикат Q (например true), который будет постусловием S, если всегда найдётся некоторый предикат Q (например true), который будет постусловием S, если  -предусловие S. -предусловие S.Для любых S и 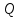 всегда найдётся некоторый предикат всегда найдётся некоторый предикат  (например false), который будет предусловием S, если (например false), который будет предусловием S, если 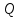 -постусловие S. -постусловие S.Для любых  и и 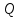 всегда найдётся программа всегда найдётся программа 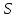 , для которой , для которой  будет предусловием, а будет предусловием, а 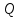 -постусловием. -постусловием.Задача программиста- найти такую программу 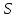 , которая завершается и для которой , которая завершается и для которой 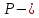 предусловие, предусловие, 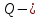 постусловие. постусловие.Установить корректность программы 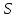 означает, что необходимо доказать соотношение означает, что необходимо доказать соотношение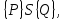 Где 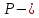 условие, которому должны удовлетворять начальные значения переменных, условие, которому должны удовлетворять начальные значения переменных,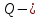 условие, которому должны удовлетворять конечные значения переменных. условие, которому должны удовлетворять конечные значения переменных.При этом соотношение 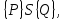 определяет только частичную корректность определяет только частичную корректность 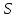 . .Определение. Оператор (программа) завершается, если его выполнение доходит до конца за конечное число шагов и за конечное время. Определение. Программа, в которой гарантируется получение требуемого результата при условии ее завершения, называется частично корректной. Определение. Если возможно показать, что программа действительно завершается за конечное число шагов при всех исходных данных, удовлетворяющих предусловию  , то программа является полностью корректной. , то программа является полностью корректной.Доказательство корректности программы 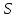 основано на основной теореме, алгоритм доказательства которой заключается: основано на основной теореме, алгоритм доказательства которой заключается:Либо в нахождении предусловия  по заданному постусловию по заданному постусловию 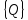 ; ;Либо проверке корректности заданных  и и 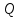 . .Схема доказательства корректности 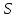 состоит из 2-х шагов: состоит из 2-х шагов:1-й шаг: формулируется некоторое утверждение о результатах выполнения 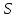 . .2-й шаг: утверждение доказывается. Пример 1. Пусть дано следующее аксиоматическое описание оператора: 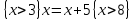 Тогда, если перед оператором 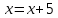 имеет место истинное предусловие имеет место истинное предусловие 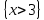 , то после выполнения оператора истинно постусловие , то после выполнения оператора истинно постусловие 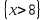 . Следовательно, в силу основной теоремы, корректность оператора . Следовательно, в силу основной теоремы, корректность оператора 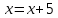 показана. показана.7.2. Слабейшее предусловие Слабейшими предусловиями называются наименьшие предусловия, обеспечивающие выполнение соответствующего постусловия. Для примера 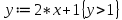 Предусловия 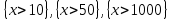 являются правильными, но слабейшим будет являются правильными, но слабейшим будет 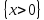 . .Если для каждого оператора ЯПВУ по заданным постусловиям можно вычислить слабейшее предусловие, то и для программы, написанной на этом ЯПВУ, может быть построено корректное доказательство. Чтобы использовать аксиоматическую семантику для доказательства правильности программ на ЯПВУ или для описания его формальной семантики, для каждого оператора языка должны быть определены аксиомы или правила вывода. 7.3. Схемы доказательства корректности программы Для доказательства основной теоремы или, что равносильно, для доказательства частичной корректности оператора (программы) 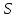 существуют специальные схемы рассуждений: существуют специальные схемы рассуждений:правило вывода; аксиомы присваивания. 7.3.1. Правила вывода Правило вывода, задающие семантику языка- это метод выведения истинности одного утверждения на основе истинности других. Правила вывода представляют собой схему рассуждений, позволяющие доказывать правильность оператора или программы. Они записываются в виде: 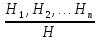 Здесь, если 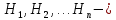 bистинные утверждения, то в bистинные утверждения, то в 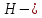 также истинное утверждение. также истинное утверждение.Рассмотрим несколько правил вывода общего характера, которые потребуются нам для доказательств корректности языковых конструкций. Правила консеквенции: А) 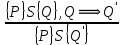 Если выполнение программы 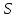 обеспечивает истинность постусловия обеспечивает истинность постусловия 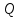 , а из , а из 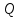 следует следует 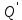 . .Б) 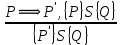 Если  следует из следует из 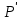 и является предусловием программы и является предусловием программы 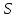 , приводящей к истинному результату , приводящей к истинному результату 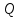 , то , то 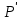 также является предусловием программы также является предусловием программы 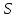 . .Правило а) ослабляет постусловие 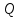 . Правило б) усиливает предусловие . Правило б) усиливает предусловие  . .Правило логического следствия: Объединяя правила консеквенции а) и б) получим правило логического следствия: 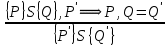 Если истинно утверждение 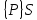 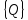 , и утверждения , и утверждения 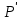 , следует утверждение , следует утверждение  , а из утверждения , а из утверждения 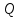 следует утверждение следует утверждение 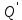 , то истинно утверждение , то истинно утверждение 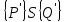 . .Правила замены: А) 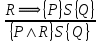 Если предикат 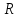 порождает логическое условие порождает логическое условие  такое, что истинно утверждение такое, что истинно утверждение 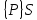 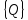 , то истинным будет и утверждение , то истинным будет и утверждение 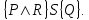 Б) 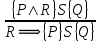 Если истинно утверждение 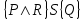 , т.е. предусловие оператора , т.е. предусловие оператора 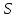 есть истинная импликация предикатов есть истинная импликация предикатов  и и 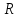 , то , то 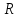 порождает условие порождает условие  такое, что такое, что 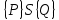 есть истинное утверждение. есть истинное утверждение.7.3.2. Аксиомы присваивания Пусть  логическое выражение. Обозначение логическое выражение. Обозначение 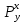 обозначает подстановку выражения обозначает подстановку выражения 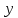 вместо всех свободных вхождений переменной вместо всех свободных вхождений переменной 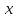 в выражение в выражение  . .Аналогично 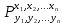 обозначает одновременную подстановку вместо всех свободных вхождений обозначает одновременную подстановку вместо всех свободных вхождений 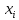 в в  соответствующего выражению соответствующего выражению 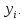 Вхождение Вхождение 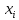 в в 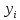 не замещаются. Переменные не замещаются. Переменные 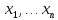 должны быть различными. должны быть различными.Аксиома- это истинное логическое утверждение (предикат), формируемое на основе подстановки. Аксиомы используются для вычисления слабейшего предусловия в простых операторах присваивания, для более сложных случаев- применяются правила вывода. 7.4. Схемы доказательств корректности некоторых операторов 7.4.1 Пустой оператор Аксиоматическое описание пустого оператора, который никаких действий не производит следующее: 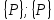 7.4.2. Оператор присваивания Синтаксис оператора присваивания следующий: <присвоить>  <переменная> = <выражение>. <переменная> = <выражение>.Выражение- это простейшие средства описания действий, которые вычисляют единственное значение, не изменяя состояния вычислений. С другой стороны, выражение- это формула для вычисления значения некоторого типа ( как правило, арифметического или логического). Оно представляет собой один 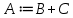 . .Рассмотрим семантику операторов присваивания и доказательства их корректности в терминах аксиом присваивания. Пусть x=E обычный оператор присваивания, Q- его постусловие. Тогда предусловие P того же оператора определяется аксиомой 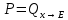 (P = (P = 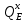 ) )Эта аксиома означает, что предусловие  вычисляется как условие вычисляется как условие 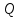 , в котором все переменные , в котором все переменные 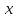 заменены переменными заменены переменными 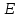 . .Пример 1. 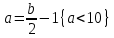 , тогда слабейшее предусловие вычисляется как , тогда слабейшее предусловие вычисляется как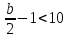 b<22, т.е. спецификация этого оператора имеет вид 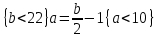 . .Пример 2. 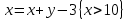 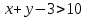 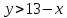 Пример 3. Доказать 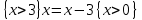 . .Доказательство состоит в проверке заданного решения предусловия. x-3>0 x>3, что и требовалось доказать. Истинность аксиомы присваивания гарантируется только при отсутствии побочных эффектов. Побочный эффект оператора присваивания может проявляться, если оператор изменяет значения переменных не входящих в его левую часть, например, никакие функции не должны изменять значения глобальных переменных. Итак, аксиоматическая семантика оператора присваивания имеет вид: 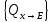 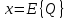 Теперь покажем, как при доказательстве корректности оператора присваивания, используются правила вывода. Пример 4. Рассмотрим утверждение 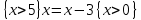 В примере 3 на основании аксиомы присваивания показано, что предусловием является соотношение 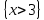 . Очевидно, что . Очевидно, что  . .Для доказательства того, что 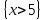 можно рассматривать как предусловие, воспользуемся правилом логического следствия, в котором P интерпретируется как можно рассматривать как предусловие, воспользуемся правилом логического следствия, в котором P интерпретируется как 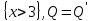 как как 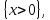 тогда получим тогда получим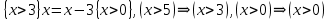  7.4.3. Группы операторов присваивания Слабейшее предусловие группы операторов описывается правилами вывода. Пусть 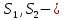 соседние операторы. При следующих предусловиях и постусловиях: соседние операторы. При следующих предусловиях и постусловиях: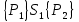 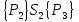 Правило вывода такой группы следующее: 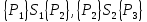 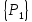 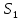 ; ; 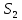 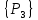 Таким образом, если 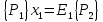 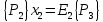 , ,то имеем 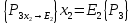 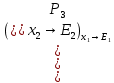 Т.е. аксиома присваивания для группы их 2-х операторов имеет следующий вид: 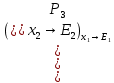 . .Это же правило вывода можно распространить на n операторов: 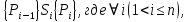 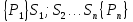 Пример 5. y=3*x+1; x=y+3; {x<10} На основании аксиомы присваивания, получим предусловие для второго оператора 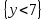 . Оно же станет постусловием для первого оператора, тогда предусловие для первого оператора вычисляется как . Оно же станет постусловием для первого оператора, тогда предусловие для первого оператора вычисляется как3*+1<7 x<2. Тогда получим 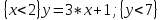 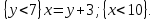 7.4.4. Оператор условного перехода Спецификация оператора условного перехода следующая: {P } if B then 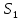 else else 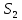 {Q} {Q}Доказательство корректности такой спецификации состоит из 2-х частей: Если B истинно, то выполняется 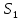 . В силу того, что P справедливо перед выполнением, то (P and B) справедливо перед выполнением . В силу того, что P справедливо перед выполнением, то (P and B) справедливо перед выполнением 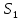 . Если Q справедливо после выполнения, то справедливо и {P and B} . Если Q справедливо после выполнения, то справедливо и {P and B} 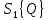 . .Если B ложно, то выполняется 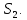 Аналогично, если P справедливо перед выполнением оператора условного перехода, то ( P and not B) Аналогично, если P справедливо перед выполнением оператора условного перехода, то ( P and not B)Справедливо перед выполнением S2. Если Q справедливо после выполнения оператора условного перехода, то справедливо и { P and not B } S2 {Q}. Если мы доказали истинность { P and B } S1 {Q} и { P and not B } S2 {Q}, то можно утверждать, что, если P справедливо перед выполнением всего оператора if, то Q будет справедливо после его выполнения независимо от того, какой оператор S1 или S2 был выбран. Итак, правило вывода имеет вид:  { P and B } S1 {Q} , { P and not B } S2 {Q} { P and B } S1 {Q} , { P and not B } S2 {Q}{ P } if B then S1 else S2 {Q} Пример 6. { ? } if (x > 0 ) then y = y – 1 else y = y + 1 end if { y > 0 } Если выбран оператор S1 , можно использовать аксиому y = y – 1 { y > 0 }. Тогда предусловие P1 = {y – 1 > 0} ={y > 1}. Для ветки S2 предусловием является P2 = {y + 1 > 0} ={y > -1}. Поскольку { y> 1} => { y > -1} , то по правилу консеквенции выбираем предусловие P2 = { y > 1 }. Тогда правило вывода для условного оператора имеет вид {P1} S1 {Q} , {P2} S2 {Q} {(P1 and B) or (P2 and not B)} if B then S1 else S2 {Q} |
