Учебное пособие по дисциплине Разработка языков программирования высокого уровня

• Название: Учебное пособие по дисциплине Разработка языков программирования высокого уровня
• Дата: 05.03.2023
• Размер: 1.74 Mb.
• Имя файла: Lektsii_YaPVU_Lukinova_2_semestr.docx
• Тип: Учебное пособие; #970477
• страница: 18 из 20

Глава 6. Основы синтаксиса языка программирования.

В середине 1950-х г в лингвистике произошла революция: ученому- лингвисту Ноаму Хомски удалось сформулировать понятие метаязыка как способа формализованного описания языка. Такой метаязык называется грамматика. Грамматики могут быть контекстно-свободными (КC), регулярными, контекстно-зависимыми и т.д.

Наиболее универсальна и проста контекстно-свободная грамматика, именно она была использована в 1960 г. разработчиками АЛГОЛА-60 Джоном Бэкусом и Питером Науром для описания синтаксиса языка. С тех пор этот способ используется всегда и носит название формы Бэкуса- Наура (БНФ).

Начнем рассмотрение синтаксиса ЯПВУ с понятия контекстно-свободной грамматики (КС-грамматики).

6.1 Основные понятия КС-грамматики.

Определение. КС-грамматика G представляет собой кортеж четырех объектов:

G={T,V,S,P},

где

1. 
   Множество Т-это конечное множество символов, из которых состоят цепочки языка. Множество Т называется множеством терминалов и цепочки представляет собой алфавит языка.
   
2. 
   Множество V-множество переменных грамматики, при этом любая переменная представляет собой класс цепочек языка, обладающих единым метасмыслом. Множество V называется еще множеством нетерминальных символов.
   
3.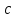 
   S V –это стартовый (начальный) символ, т.е. переменная, которая представляет определяемый язык. Другие переменные позволяют доопределить описываемый язык, задаваемый стартовым символом.
   
4. 
   Множество P –это множество продукций или правил вывода, которые представляют собой правила образования цепочек языка. Таким образом, предложения языка создаются с помощью последовательности продукций, начиная со стартового символа –этот процесс называется порождением или выводом и обозначается символами или .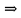
   

Определение. Если кортеж G есть КС-грамматика, то язык L(G), описываемый этой грамматикой, представляет собой множество терминальных цепочек w, порожденных из стартового символа S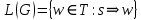



G

Рассмотрим введенные понятия на примере языка палиндромов. Палиндром pal –это цепочка w, читаемая как слева направо, так и справа налево: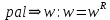

,

Где 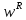- обращение цепочки, т.е. цепочка, прочитанная справа налево.

Пусть Т={0,1}, тогда язык палиндромов над алфавитом Т представляется множеством Lpal={0,1,101,1001,….}. Определим грамматику, т.е. множества V,S,P для языка палиндромов Lpal следующим образом:

V={A},S=A,

P: A 0

A 1

A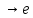

A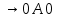

A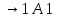

Продукционные правила Р обозначают: если цепочка w равна или принадлежит переменной А, то цепочки 0,1,е, 0А0 или 1А1, тоже принадлежат А: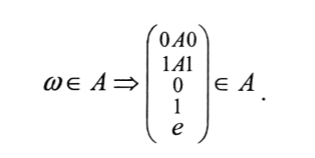

Пусть требуется вывести цепочки 101, 1001. В грамматике языка палиндромов Lpal порождение требуемых цепочек выглядит следующим образом:

А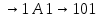

А .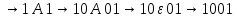

Теперь опишем грамматику арифметических выражений.

Пусть

Т={+,*,(,),a,b,0,1};

V={E,I,}, где E –множество выражений; I-идентификатор, начинающийся с буквы а или b;

S=E;

P: I a|b|aI|bI|I0|I1

E I|E+E|E*E|(E)

В описанной грамматике требуется получить порождение следующих арифметических выражений а*(а+b00),(b0101)*(a101).

1. 
   Порождение цепочки a*(a+b00):
   

E E*E E*(E) I*(E) I*(E+E) a*(E+E) a*(I+E) a*(I+I) a*(a+I) a*(a+I0) a*(a+I00) a*(a+b00).

2. 
   Порождение цепочки (b0101)*(a101):
   

E→E*E→(E)*E→(E)*E→(E)*(E)→(I)*(E)→(I)*(I)→(I1)*(I)→(I01)*(I)→(I101)*(I)→(I0101)*(I)→(b0101)*(I1)→(b0101)*(I1)→(b0101)*(I01)→(b0101)*(I101)→(b0101)*(a101)