Л_Р Физика атомов и молекул_43_44_46_52. Учебное пособие по выполнению лабораторных работ по физике (модуль 6 Атомная физика) для студентов инженернотехнических направлений подготовки
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
Классическая модель атома водородаРассмотрим атом водорода и сходные с ним ионы (модель так называемого водородоподобного атома), т. е. предположим, что имеется атомная система, состоящая из ядра с зарядом Zе и одного электрона с зарядом -е, где Z — порядковый номер элемента в периодической системе Д. И. Менделеева. Кулоновская сила f взаимодействия между ядром и электроном играет роль центростремительной силы, равной для круговой орбиты 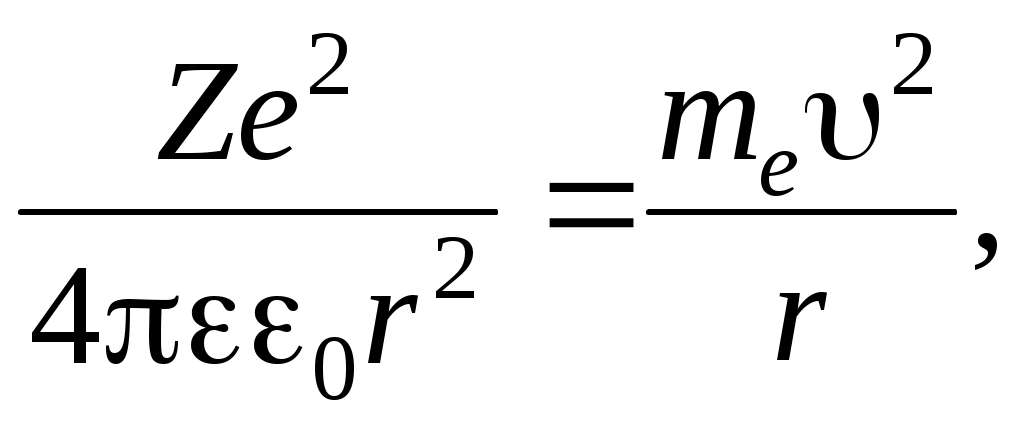 (43.2) (43.2)где те — масса электрона; r — радиус орбиты. В электрическом поле ядра электрон обладает потенциальной энергией Полная энергия электрона равна сумме потенциальной и кинетической энергий. С учетом (43.2) и (43.3) и знаков в этих выражениях Согласно представлениям классической электромагнитной теории, вращающийся по орбите электрон возбуждает вокруг себя переменное электромагнитное поле, распространяющееся в пространстве со скоростью света. Ускоренно движущийся электрон при своем вращении вокруг ядра должен излучать и вследствие этого терять часть энергии. Таким образом, согласно классической механике, энергия электрона все время должна уменьшаться. Из формулы (43.4) следует, что меньшему значению энергии (с учетом знака) соответствует меньший радиус. В результате электрон должен “упасть” на ядро. Из формулы (43.2) следует, что с уменьшением радиуса орбиты скорость движения электрона возрастает, т. е. период обращения уменьшается. Это должно привести к непрерывному увеличению частоты излучаемых электромагнитных волн, и атом должен излучать непрерывный (сплошной) спектр. Однако в действительности атом — устойчивая система и излучает лишь линейчатый спектр. Выход из создавшегося противоречия был предложен Бором. Теория водородоподобного атома по Бору. Основываясь на гипотезе Планка о квантовом характере излучения и поглощения, Бор сформулировал законы, описывающие состояние и движение электронов в атоме в виде определенных постулатов, которые дают объяснение экспериментальным данным. Первый постулат Бора. Электрон в атоме может вращаться только по строго определенным стационарным орбитам, радиусы которых определяются из условия где L — момент импульса электрона; п — главное квантовое число, принимающее положительные целые значения 1, 2, ... и определяющее принадлежность электрона к той или иной орбите; h — постоянная Планка. Все другие орбиты “запрещены”. Таким образом, Бор постулировал, что энергия электрона в атоме может принимать строго определенные дискретные значения E1, Е2, , Еn, Вращаясь по стационарным орбитам, электрон не излучает и не поглощает электромагнитных волн. Второй постулат Бора. Излучение происходит лишь при переходе электрона из стационарного состояния с большим значением энергии Еk. в другое стационарное состояние с меньшим значением энергии Еi. При этом излучается квант энергии (фотон) строго определенной частоты. Частота определяется фундаментальным соотношением (условие частот Бора) где — частота излученного фотона. Поскольку частота фотона и его длина волны связаны между собой соотношением то условие Бора можно переписать для значений длин волн Из соотношения (43.8) следует, что излучение происходит при переходе электрона с внешних орбит на внутренние. Если же электрон переходит с внутренних орбит на внешние, то энергия поглощается. Вычислим радиусы стационарных орбит и полную энергию электрона в водородоподобном атоме. С учетом (43.2) и условия квантования Бора (43.5) имеем для значений радиусов стационарных орбит и энергий стационарных состояний соответственно 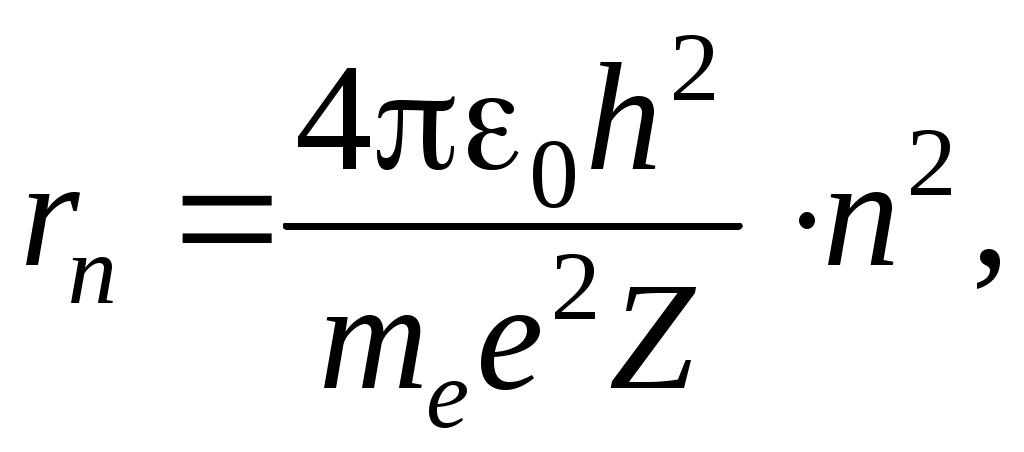 (43.9) (43.9)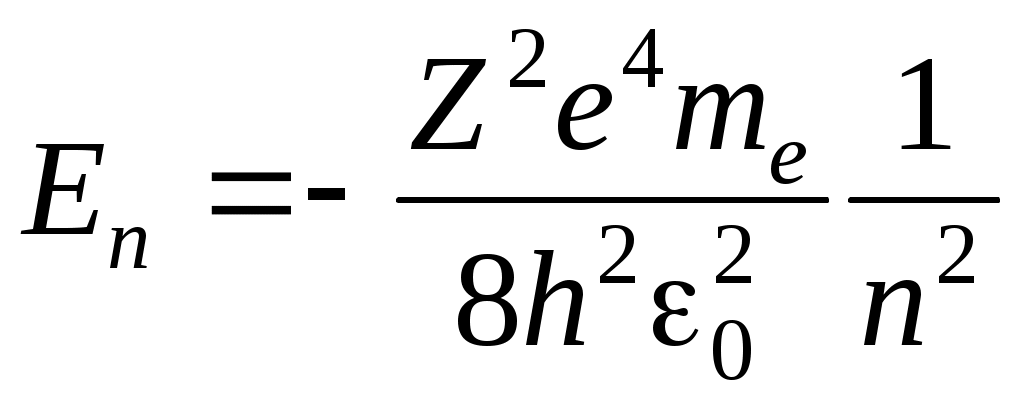 , (43.10) , (43.10)где n= 1, 2, …. Из формулы (43.10) следует, что квантовое число п определяет энергию электрона в атоме, так как остальные величины остаются постоянными. Основное состояние атома с наименьшей энергией характеризуется значением главного квантового числа n = 1. Состояния с n > 1 называются возбужденным. В эти состояния атом переходит, поглощая извне дополнительную энергию, достаточную для данного перехода. Атомы из возбужденных состояний самопроизвольно переходят в состояния с меньшей энергией, выделяя при этом квант энергии Энергия испускается в виде электромагнитного излучения, длина волны которого определяется по формуле (43.8). Подставив в выражение (43.8) значение энергии из (43.10) при Z = 1 получим  . (43.12) . (43.12)Значение R совпадает с постоянной Ридберга, а n в формуле Бальмера приобретает смысл главных квантовых чисел. Следует подчеркнуть, что экспериментально найденное значение постоянной Ридберга отличается от теоретического значения, что видно из следующих данных: Rтеор = 109737,303 см-1; Rэкс = 109677,581 см-1. ОПИСАНИЕ АППАРАТУРЫ И МЕТОДА ИЗМЕРЕНИЙ Установка состоит из водородной лампы и измерительного устройства, в качестве которого применен монохроматор типа МУМ (Монохроматор универсальный малогабаритный МУМ1.720.012-01), который предназначен для выделения монохроматического излучения в области спектра от 200 до 800 нм. Оптическая схема монохроматора приведена на рисунке 43.2. Излучение от лампы 1 через конденсор 2 попадает на входную щель (коллиматор) 3 и посредством зеркала 4 заполняет вогнутую дифракционную решетку 5, которая играет роль фокусирующего и диспергирующего элемента. Дифрагированное решеткой излучение направляется в выходную щель 7 (при выведенном плоском зеркале 6) или в выходную щель 8 (при введенном зеркале 6). 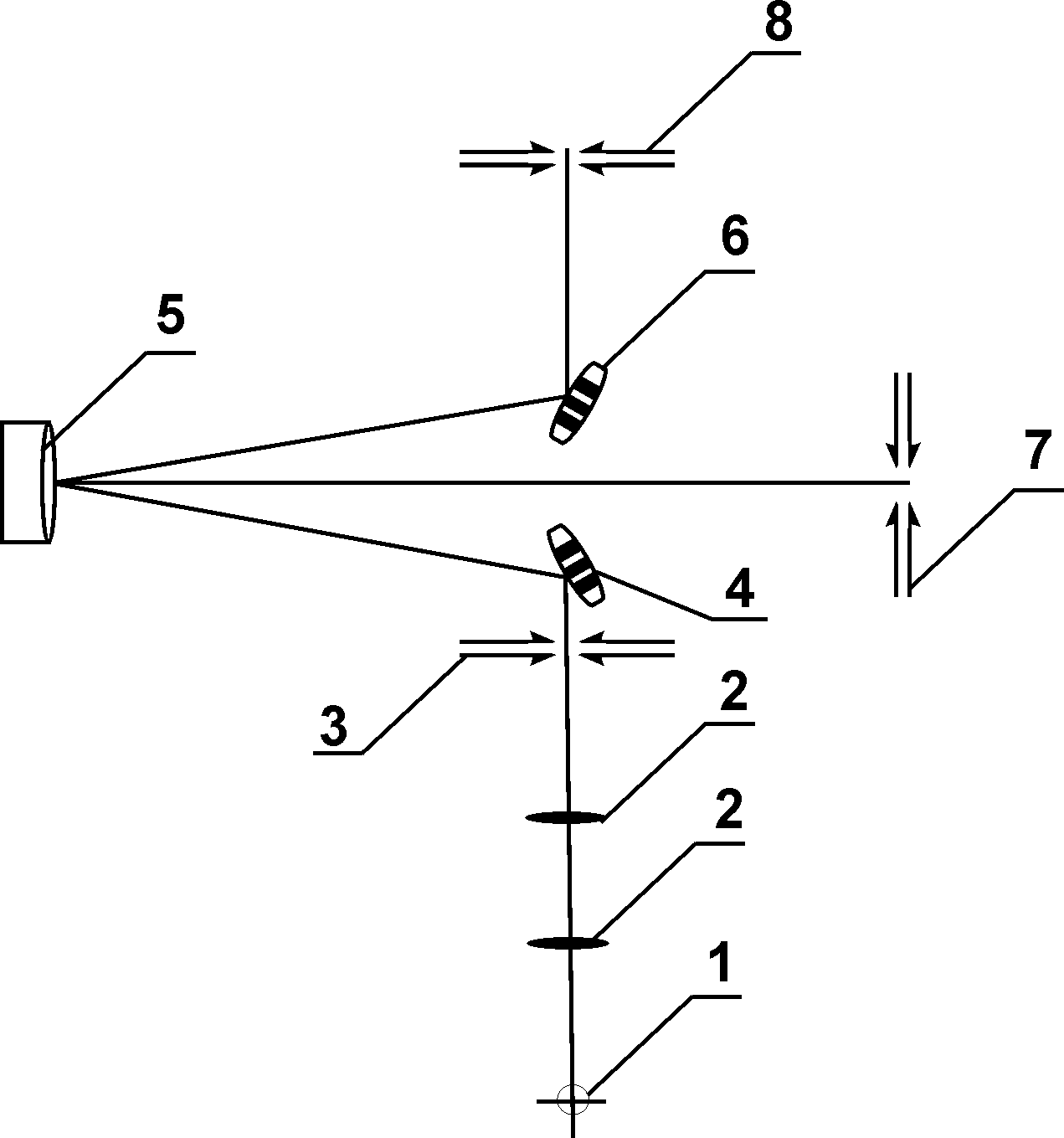 Рисунок 43.2 - Оптическая схема монохроматора МУМ 1.720.012-01. Для получения большей спектральной чистоты выделяемого излучения при работе в области спектра от 330 до 660 нм входная и выходные щели устанавливаются в «положение I», а при работе в области спектра от 200 до 260 и от 730 до 800 нм щели устанавливаются в «положение II», в областях от 660 до 730 им и от 260 до 330 нм, входная -- в «положение II», и выходная - в «положение II». Переключение зеркала 6 осуществляется перемещением от себя (к себе) рукоятки, расположенной на боковой стенке корпуса монохроматора со стороны выходной щели. Сканирование спектра осуществляется поворотом решетки 5 (рис. 43.2), с помощью рукоятки, расположенной на торцевой стенке монохроматора. В корпус монохроматора вмонтирован цифровой механический счетчик, посредством которого осуществляется непосредственным отсчет длин волн с точностью ±0,2 нм.  Рисунок 43.3 - Внешний вид монохроматора МУМ 1.720.012-01. Принцип действия установки основан на разложении монохроматором излучения водородной лампы, входящей в состав излучателя, в линейчатый спектр. В процессе выполнения лабораторных работ производится исследование спектра атомарного водорода, наблюдение спектральных линий и измерение длин их волн с помощью монохроматора. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Подключите сетевой шнур излучателя к сети и включите установку выключателем СЕТЬ на задней панели излучателя (при этом должна светиться подсветка клавиши выключателя СЕТЬ). Дать прогреться излучателю в течение 3-5 мин. Через окуляр монохроматора, вращая ручку измерения длин волн, наблюдайте линии спектра. Для измерения длины волны установите соответствующую линию, начиная с красной, в центре поля наблюдения монохроматора и по шкале определите длину волны. Полученные значения длины волны необходимо занести в таблицу 43.1. Вычисляют постоянную Ридберга по опытным данным для каждой линии, используя формулу Бальмера (43.1) Из полученных значений определяют среднее значение постоянной Ридберга и рассчитывают абсолютную и относительную погрешности. Таблица 43.1
Записывают в виде Вычисляют относительную погрешность По окончании работы необходимо отключить питание установки выключателем СЕТЬ (на задней панели излучателя) и отключить сетевую вилку излучателя от питающей сети. КОНТРОЛЬНЫЕ ВОПРОСЫЧто такое спектр? Сформулировать постулаты Бора. Перечислить серии спектра водорода. Какому переходу соответствует головная линия каждой серии. Чем определяется граница каждой серии? Почему к границе серии интенсивность линии уменьшается? Каким электронным переходам соответствуют самые интенсивные линии видимой части спектра водорода. Объясните смысл отрицательного значения энергии электрона в атоме. Каков физический смысл квантовых чисел? Вычислить радиус орбиты электрона и энергию электрона на орбите. ЛАБОРАТОРНАЯ РАБОТА № 44 | |||||||||||||||||||||||||||||||||||
