Л_Р Физика атомов и молекул_43_44_46_52. Учебное пособие по выполнению лабораторных работ по физике (модуль 6 Атомная физика) для студентов инженернотехнических направлений подготовки
 Скачать 2.11 Mb.
|
Оптические спектры атомов ртути и неонаЦЕЛИ РАБОТЫ:1. Градуирование спектрометра-монохроматор УМ-2. 2. Оценка максимальных и минимальных энергий и импульсов фотонов, излученных атомами неона 3. Оценка максимальных и минимальных длин волн и частот полос в сплошном спектре лампы накаливания в видимой области. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: универсальный спектрометр-монохроматор УМ-2, ртутная лампа с пусковым устройством, неоновая лампа, лампа накаливания, оптическая скамья с рейтерами. Теоретические сведения Спектры атомовВо второй половине XVII в. Исааку Ньютону удалось при помощи стеклянной призмы разложить тонкий пучок солнечного света на составляющие цвета: фиолетовый, синий, голубой, зеленый, желтый, оранжевый и красный. Воспользовавшись второй призмой, он смог снова соединить полный спектр в пучок белого света, но если исключался один из цветов, то уже никакие операции не могли ничего изменить и привести к получению белого света. Развертывание пучка белого света в спектр носит название дисперсии. Саму радужную полоску Ньютон назвал спектром (от латинского spectrum – видение). Разложение света на составляющие его компоненты называется получение оптического спектра излучения. Например, видимый спектр наблюдается в радуге при разложении солнечного света на составляющие его компоненты на дождевых каплях. Видимый спектр, однако, только маленькая часть электромагнитного спектра, который простирается от области рентгеновского излучения до радиоволн. На рисунке 44.1 приведена шкала электромагнитных волн. Физическая природа излучения одинакова по всей шкале. Во всех областях волны имеют одну и ту же скорость распространения, одинаковую электромагнитную природу, и одна часть шкалы отличается от другой только энергией излучения, а, следовательно, и частотой. Области с тем или иным названием перекрываются. Однако названия все же связаны с определенными источниками. Радио- и микроволновое излучение создается электронами, движущимися в проводниках (например, в антеннах) с ускорением. Микроволновое излучение также создается электронами, 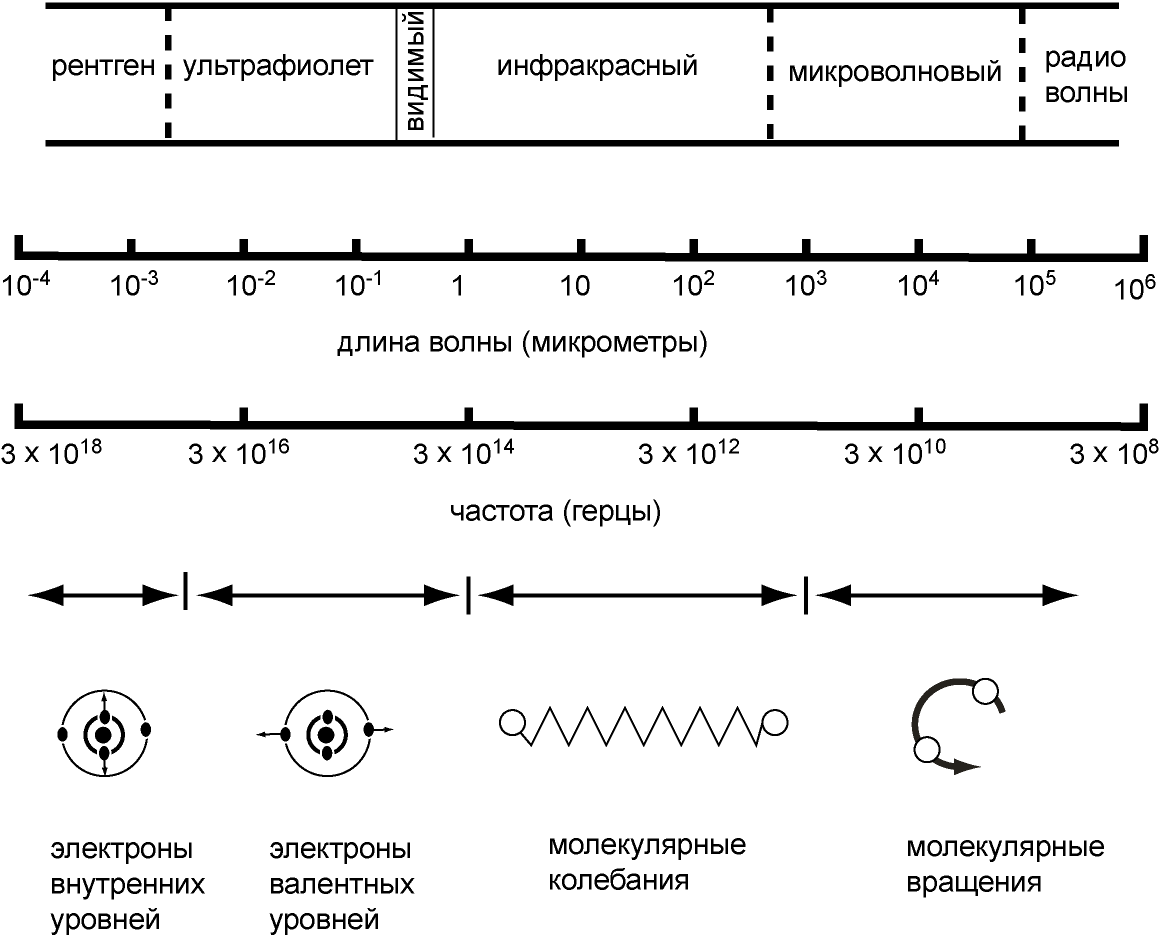 Рисунок 44.1 – Шкала электромагнитных волн которые совершают молекулярные вращения. Между микроволнами и видимым светом лежит область теплового излучения. Это излучение испускается при столкновениях молекул в горячих газах или твердых телах. Столкновения молекул вызывают колебания находящихся в них зарядов; при этом испускается электромагнитное излучение более высоких частот, чем мы можем получить от контуров, созданных руками человека. Ультрафиолетовая и видимая область образуются при переходе электронов на внешних уровнях, которые участвуют в химических реакциях, и называются валентными. Энергия фотонов в рентгеновской области спектра излучается атомами при переходе электрона во внутренних уровнях, а также рентгеновское излучение получают при торможении быстрых электронов в рентгеновских трубках. При очень высоких частотах мы приходим к гамма-лучам. Они испускаются самопроизвольно при некоторых процессах радиоактивного распада. В этой работе мы будем изучать только видимую часть шкалы электромагнитных волн. Видимая часть спектра соответствует частотам между 41014 и 7,51014 Гц. К оптическому излучению относится видимое, инфракрасное и ультрафиолетовое излучения в диапазоне длин волн от 10-3 до 10-9 м. Если в источнике света содержатся все цвета, т.е. наблюдается полная картина радуги, такой спектр называется непрерывным или сплошным. Излучение, испускаемое нагретыми твердыми телами и жидкостями, содержит весь диапазон длин волн видимого света, т.е. обладает непрерывным спектром. Если же в источнике света какие-нибудь цвета будут отсутствовать, то в радужной картине на месте этих цветов появятся темные полосы. При свечении молекулярных газов и паров возникают так называемые полосатые спектры – спектры, состоящие из отдельных полос, разделенные темными промежутками. Спектр излучения атомарных газов и паров металлов представляет собой набор отдельных линий с характерными значениями длин волн (частот) и называется линейчатым спектром. Можно сказать, что вещества, в которых атомы расположены на значительных расстояниях друг от друга так, что их можно считать изолированными, обладают линейчатыми спектрами. Вещества, в которых атомы объединились в молекулы, наблюдаются полосатые спектры. Если молекулы связаны между собой, как они связаны в жидкости или твердом теле, то наблюдаются непрерывные спектры. Рассмотрим, как происходит элементарный акт излучения. Согласно квантовым представлениям, энергия электронов в атоме может принимать не любые, а только некоторые определенные значения, образующие дискретный набор, так называемые стационарные уровни энергии. Атом, получив энергию извне, возбуждается, что выражается в переводе на более высокий уровень Ei внешних электронов. Оптические частоты возникают обычно при относительно небольшом возбуждении атома. Состояние возбуждения длится недолго ( 10-8 с), после этого электрон возвращается на уровень с меньшей энергией Ek, разрешенный правилами отбора. Переход сопровождается излучением фотона с энергией  . (44.1)Спектральная линия возникает при одновременном излучении одинаковых фотонов множеством атомов. Спектр каждого атома уникален, так как уникален дискретный набор его стационарных уровней энергии. Яркость спектральных линий зависит от того, какова вероятность перехода, соответствующего излучению данной спектральной линии. Любое вещество не только характеризуется своим спектром излучения, но и поглощает электромагнитные волны только определенных частот. В отличие от спектра испускания, который получается при разложении излученного телом света, спектр поглощения возникает, когда вещество поглощает из белого света отдельные спектральные линии. Если пропустить белый свет сквозь холодный, неизлучающий газ, то на фоне непрерывного спектра источника появляются темные линии. Газ поглощает наиболее интенсивно свет как раз тех частот, которые он испускает в сильно нагретом состоянии. Темные линии на фоне цветной радуги – это линии поглощения, образующие в совокупности спектр поглощения. Твердые тела и жидкости имеют широкие области поглощения. Атомарные газы и пары поглощают только излучения с теми длинами волн, которые они сами излучают. Это так называемые линии поглощения. Как и спектр испускания, спектр поглощения используется при спектральном анализе для обнаружения и идентификации веществ. Наиболее изученным спектром поглощения является солнечный спектр. При прохождении света через газовую оболочку Солнца возникают многочисленные линии поглощения, которые называются фраунгоферовыми линиями. Количество и расположение линий в спектре излучения или поглощения атомарного газа зависят от структуры химического элемента. По спектру излучения с помощью спектрального анализа можно выявлять наличие отдельных элементов в соединении и определять химический состав вещества. Спектральный анализ илиспектроскопия занимается анализом спектров испускания (эмиссионных спектров) и спектров поглощения (абсорбционных спектров) атомов и молекул. Спектроскоп (спектрометр) - инструмент для анализа спектра. Он содержит коллиматор, собирающий излучение от источника; дифракционную решетку или призму, которая разлагает излучение на составляющие; и зрительную трубу для регистрации излучения. Дисперсией света называется зависимость показателя преломления n вещества от частоты (длины волны) света или зависимость фазовой скорости световых волн от его частоты . Угол отклонения лучей призмой зависит от величины преломляющего угла призмы и от величины   . (44.2)где n– показатель преломления стекла; Аn–функция длины волны, поэтому лучи разных длин волн после прохождения призмы окажутся отклоненными на разные углы, т.е. пучок белого света за призмой разлагается в спектр, что и наблюдалось Ньютоном. Рассмотрим различия в дифракционном и призматическом спектрах. Дифракционная решетка разлагает падающий свет непосредственно по длинам волн, поэтому по измеренным углам (по направлениям соответствующих максимумов) можно вычислить длину волны. Разложение света в спектр в призме происходит по значениям показателя преломления, поэтому для определения длины волны света надо знать зависимость n = f(). Составные цвета в дифракционном и призматическом спектрах располагаются различно. В дифракционной решетке синус угла отклонения пропорционален длине волны. Следовательно, красные лучи, имеющие большую длину волны, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи в спектр по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны уменьшается. Поэтому красные лучи отклоняются призмой слабее, чем фиолетовые. Величина  , (44.3)называемая дисперсией вещества, показывает, как быстро изменяется показатель преломления с длиной волны. Показатель преломления для прозрачных веществ с уменьшением длины волны увеличивается; следовательно, величина  по модулю также увеличивается с уменьшением . Такая дисперсия называется нормальной.Ширину спектральной линии можно объяснить, используя соотношение неопределенностей для энергии Е и времени t. Неопределенности этих величин удовлетворяют условию  , (44.4)где  - неопределенность энергии некоторого состояния системы,  - промежуток времени, в течение которого оно существует. Следовательно, система, имеющая среднее время жизни , не может быть охарактеризована определенным значением энергии; разброс энергии  возрастает с уменьшением среднего времени жизни. Из выражения (44.4) следует, что частота излученного фотона также должна иметь неопределенность  , т.е. линии спектра должны характеризоваться частотой, равной  . Опыт действительно показывает, что все спектральные линии размыты. Измеряя ширину спектральной линии, можно оценить порядок времени существования атома в возбужденном состоянии.Спектр водородоподобных атомов Разреженные газы (возбужденные атомы) дают излучение, состоящее из отдельных линий (линейчатый спектр). Распределение этих линий для большинства атомов представляет собой сложную картину, но для атома водорода и водородоподобных систем она достаточно проста. Спектры таких атомов представляют собой группы (серии) линий, причем, эти серии четко разделены, и находятся в инфракрасной, видимой и ультрафиолетовой частях спектра. Наиболее простой линейчатый спектр – спектр атомарного водорода – состоит из нескольких серий: серии Лаймана в ультрафиолетовой области, серии Бальмера в видимой области, серий Пашена, Брэкета, Пфунда и Хэмфри в инфракрасной области спектра. Закономерность расположения линий в спектре водорода выражается эмпирической формулой Бальмера  , (44.5)где – длина волны спектральных линий,R- постоянная Ридберга (R = 1,09737107 м-1), niи nk –целые числа от 1 до , причем nk= ni+1. В серии Лайманаni =1; nk = 2,3,…; Бальмераni= 2; nk= 3,4,…; Пашена ni = 3; nk = 4,5…. Для объяснения экспериментальных данных Нильс Бор, используя планетарную модель атома, создал теорию атома водорода, в основу которой вошли два постулата. Первый постулат Бора (постулат стационарных состояний): атомы могут пребывать только в определенных стационарных состояниях, в которых, несмотря на происходящие в них движения заряженных частиц они не излучают, и не поглощают энергию. В этих состояниях атомы обладают энергиями, образующими дискретный ряд Е1, Е2, …, Еn. Состояния эти характеризуются своей устойчивостью, всякое изменение энергии в результате поглощения или испускания электромагнитного излучения или в результате соударения атомов может происходить только при полном переходе (скачком) из одного состояния в другое. Правило квантования орбит Бора утверждает, что в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантованные значения момента импульса, удовлетворяющие условию  (44.6)где  - масса электрона; - скорость электрона;  - радиус его орбиты;h – постоянная Планка. Второй постулат Бора (правило частот) устанавливает, что при переходе атома их одного стационарного состояния в другое излучается или поглощается один фотон. Излучение происходит при переходе атома из состояния с большей энергией в состояние с меньшей энергией (при переходе электрона с более удаленной от ядра орбиты на ближнюю к ядру орбиту). Поглощение фотона сопровождается переходом атома в состояние с большей энергией – этому соответствует переход электрона на более удаленную от ядра орбиту. Математически правило частот Бора может быть записано следующим образом:  , (44.7)где Еn , Еm – энергия атома в двух стационарных состояниях;  – энергия излученного или поглощенного фотона. При Еm> Еn происходит поглощение фотона, при Еm< Еn – его излучение.Эти постулаты резко противоречат положениям классической физики. 1. В классической механике предполагается, что при переходе системы из одного энергетического состояния в другое энергия системы меняется непрерывно, принимая все промежуточные значения. 2. Электрон, находясь на круговой орбите, движется с центростремительным ускорением, следовательно, согласно классической электродинамике, он должен излучать электромагнитные волны, т.е. терять энергию и в конце концов упасть на ядро (причем, это должно случиться достаточно быстро за время  с).Хотя эти постулаты и противоречат классической физике, определение радиуса орбиты электрона и его энергии на этой орбите ведется с помощью классической физики. Рассмотрим электрон, движущийся в поле атомного ядра с зарядом Ze. При Z = 1 такая система соответствует атому водорода, при других значениях Z - водородоподобному иону, т.е. атому с порядковым номером Z, из которого удалены все электроны, кроме одного. Уравнение движения электрона имеет вид:  . (44.8)Исключив из уравнений (44.6) и (44.8), получим выражение для радиусов допустимых орбит  (n = 1, 2, 3,….). (44.9)Радиус первой орбиты электрона в атоме водорода называется боровским радиусом (боровский радиус принято обозначать символом  или а0 вместо r1) А. (44.10)Внутренняя энергия атома складывается из кинетической энергии электрона (ядро считаем неподвижным) и энергии взаимодействия электрона с ядром:  . (44.11)Знак минус отражает заряд электрона. Из (44.8) следует, что  . (44.12)Следовательно,   (44.13)Подставив сюда выражение (44.9), найдем допустимые значения внутренней энергии атома:  , (n = 1,2,3,….). (44.14)Зависимость энергии атома от квантового числа n можно представить на диаграмме энергетических уровней, где по одной из осей отложены значения энергии Еn (рисунок 44.2). Состояние Е1 с наименьшей возможной энергией является основным, все другие Е2, Е3, Е4,… возбужденными состояниями. Изменение энергии электрона при переходе между состояниями могут быть символически изображены на той же диаграмме стрелками, проведенными из начального состояния в конечное состояние. В 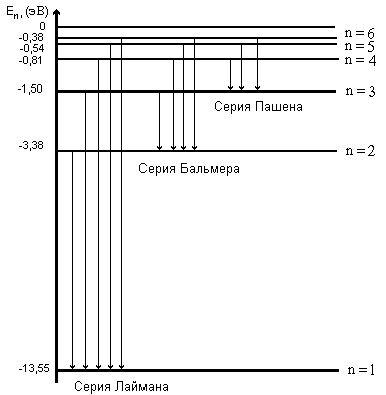 се линии, относящиеся к переходам на один и тот же уровень, образуют серию. Так, при m= 1, n меняется от 2 до бесконечности, что соответствует серии Лаймана; при m= 2, n меняется от 3 до бесконечности, что соответствует серии Бальмера и т.д. Рисунок 44.2 – Спектр атома водорода. Планетарную теорию атома нельзя считать до конца правильной. Тот факт, что она приводит к хорошим результатам для атома водорода, в частности, она дает точное значение постоянной Ридберга, скорее случаен. Однако, это послужило мощным толчком к развитию квантовой теории атома. Сам Н. Бор рассматривал свою теорию как промежуточный этап в поисках более верной теории атома. И такая теория в квантовой механике теперь существует. Подтвержденная экспериментально, гипотеза де Бройля о корпускулярно-волновом дуализме свойств вещества коренным образом изменила представления о свойствах микрообъектов. Состояние частиц в квантовой механике описывается принципиально по-новому – с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах. Статистическое толкование волн де Бройля и соотношение неопределенностей Гейзенберга привело к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны. Такое уравнение предложено в 1926 г. Э. Шредингером и является основным уравнением нерелятивистской квантовой механики  , (44.15)где  , m- масса частицы, - оператор Лапласа,i- мнимая единица,U(x, y, z) – потенциальная энергия частицы в силовом поле, в котором она движется, (x, y, z) – волновая функция частицы. Квантовая механика отказывается от классического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема. Электрон при своем движении как бы “размазан” по всему объему, образуя электронное облако. Решая уравнение Шредингера можно определить все энергетические уровни электрона в атоме и все функции состояния. В основном состоянии электрон характеризуется 1-ой волновой функцией. Все возбужденные состояния n2 – кратно вырождены. Состояния электрона в атоме определяются четырьмя квантовыми числамисоответственно четырем степеням свободы, связанным с тремя пространственными координатами и спином. Это: n - главное квантовое число (определяет энергию электрона в атоме: n = 1, 2, 3); l - орбитальное квантовое число (определяет момент импульса электрона: l= 0, 1, 2,…, n-1); m– магнитное квантовое число (определяет проекцию момента импульса на направление внешнего магнитного поля: m = - l, …, 0, …, + l; ms- магнитное спиновое число (определяет собственный механический момент импульса электрона). Электрон обладает собственным неуничтожимым механическим моментом импульса - спином. Спиновое число электрона принимает только два значения, и характеризует направление магнитного момента электрона относительно внешнего магнитного поля ms= 1/2. Квантовые числа nи lхарактеризуют размер и форму электронного облака, mхарактеризует ориентацию электронного облака в пространстве. Число возможных переходов электрона в атоме, связанных с испусканием и поглощением света ограничено правилами отбора: 1) изменение орбитального квантового числа удовлетворяет условию l= 1; 2) изменение магнитного квантового числа удовлетворяет условию m= 0, 1. ОПИСАНИЕ УСТАНОВКИ И МЕТОДЫ ИЗМЕРЕНИЙ В лабораторной работе универсальный прибор УМ-2 будет использован как спектрометр. Схема универсального спектрометра - монохроматора УМ-2 дана на рисунке 44.3. Основные узлы прибора: коллиматор, система призм и столик с поворотным механизмом, зрительная труба. Коллиматор (от лат. «collimo» - выпрямитель) предназначен для получения параллельных пучков света. От источника S на входную щель спектрометра (1), расположенную в фокальной плоскости объектива коллиматора (3), падает расходящийся пучок света. Щель регулируется по ширине микрометрическим винтом (2). Система призм и столик с поворотным механизмом. Из объектива коллиматора параллельный пучок лучей проходит через систему призм (5), установленную на столике с поворотным механизмом (6). Столик вращается вокруг вертикальной оси при помощи микрометрического винта с барабаном (7). На барабан нанесена спиральная канавка с относительными градусными делениями от 0 до 3500. Цена деления шкалы 2. Отсчет читается против индекса, скользящего по спиральной канавке. При вращении барабана столик с призмами медленно поворачивается, и в поле зрения появляются различные участки спектра. Зрительная труба. Объектив зрительной трубы (8) дает изображение входной щели в своей фокальной плоскости (12). В этой же плоскости расположен треугольный указатель спектральных линий, освещенный специальной лампочкой. Изображение и указатель рассматривают через окуляр (9). Массивный корпус прибора (10) предохраняет его от повреждений и загрязнения. На оптической скамье перед входной щелью спектрометра поочередно помещается ртутная, неоновая и лампа накаливания. 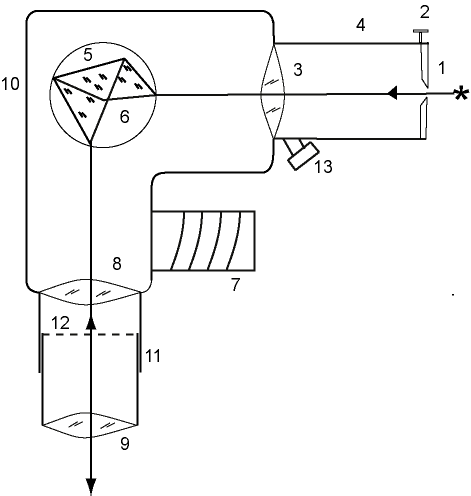 Спектрометр-монохроматор УМ-2 позволяет нам определить углы преломления всех видимых линий в спектрах. Чтобы замерять длины волн линий или полос в спектрах, необходимо проградуировать спектрометр – монохроматор УМ2 с помощью ртутной лампы. Для градуирования выбран спектр ртути, так как он содержит богатый набор спектральных линий в видимой области. Рисунок 44.3 – Спектрометр – монохроматор УМ – 2. Градуирование в данном случае заключается в построении графика зависимости длин волн спектральных линий ртути и отсчетов по шкале спектрометра о, соответствующих этим линиям и определяющих положение линий в спектре. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Задание 1. Градуирование спектрометра. Ртутную лампу устанавливают на оптической скамье перед входной щелью спектрометра, включают ее в сеть через пусковое устройство, и дают ей прогреться в течение 5 мин. Движением окуляра получают резкое изображение треугольного указателя спектрометра и спектральных линий. Затем подбирают удобную для измерений ширину щели, открывая или закрывая ее с помощью микрометрического винта (2, см. рисунок 44.3). Производят сканирование спектра ртути (англ. «scan» - поле зрения) т.е. последовательно просматривают спектр, подводя к треугольному указателю спектрометра спектральные линии от фиолетовой до красной. Для каждой линии делают отсчет по спиральной шкале. Результаты измерений записывают в таблицу 44.1. Таблица 44.1.
По полученным данным (таблица 44.1) строится график длин волн спектральных линий ртути от углов о, соответствующих этим линиям и определяющих их положение в спектре. Градуировачную кривую строят на миллиметровой бумаге, откладывая по оси абсцисс λ нм, а по оси ординат о. Задание 2. Оценка максимальных и минимальных энергий и импульсов фотонов, излученных атомами неона в видимой области. Помещают вблизи входной щели спектрометра неоновую лампу, включают ее в сеть. Получают хорошее изображение спектра. Находят в спектре неона линии указанные преподавателем, и снимают для них отсчет по шкале прибора 0. Результаты записывают в таблицу 44.2. Пользуясь градуировочным графиком, определяют длины волн для данных линий. Таблица 44.2.
Энергию фотонов находят по формуле  ,где с = 3108 м/c, h = 6,62510-34 Джс. Результаты выражают в Джоулях и электрон-вольтах. Импульс фотонов можно оценить по формуле  .Задание 3. Оценка максимальных и минимальных длин волн и частот полос в сплошном спектре лампы накаливания в видимой области. Помещают вблизи входной щели спектрометра лампу накаливания, включают ее в сеть. Получают хорошее изображение спектра. Находят в сплошном спектре значения омин и омаксдля начала и конца красной, зеленой и синей полосы. Полученные значения записывают в таблицу 44.3. Пользуясь градуировочным графиком, определяют длины волн λмин и λмакс, соответствующие значениям омин иомаксдля каждой полосы. Рассчитывают частоту νмин и νмакс для начала и конца красной, зеленой и синей полосы по формуле  .Таблица 44.3.
Требование к содержанию отчета: итоги лабораторных экспериментов представить в виде градуировочного графика о от λ, который приводится на миллиметровке. При построении графика некоторые экспериментальные точки оказываются смещенными от плавной кривой. Чаще всего такие “выбросы” свидетельствуют о неправильной расшифровке спектральных линий. В этом случае необходимо еще раз сопоставить наблюдаемую картину с таблицей спектральных линий. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, нм