Романюк В.А. Основы радиосвязи. Учебное пособие В. А. Романюк

• Название: Учебное пособие В. А. Романюк
• Анкор: Романюк В.А. Основы радиосвязи.doc
• Дата: 16.03.2018
• Размер: 1.41 Mb.
• Имя файла: Романюк В.А. Основы радиосвязи.doc
• Тип: Учебное пособие; #16756
• страница: 3 из 7

к горизонтальной оси tgд называют тангенсом угла диэлектрических потерь, который определяется формулой
(1.15)
Для высококачественных диэлектриков tgд→0

Диэлектрики и проводники

Как следует из (1.14) и (1.15), соотношение между мнимой и действительной частями , т.е. tgд зависит от частоты колебаний. Поскольку плотность тока в среде равна сумме плотности тока проводимости и смещения,

то величина tgд рана отношению плотности тока проводимости к плотности тока смещения. Таким образом, в одной и той же среде на разных частотах могут преобладать либо только токи проводимости, либо токи смещения, т.е. среда на одних частотах может быть проводником, а на других – диэлектриком.

Если колебания E(t) и H(t) происходят с частотой
,
то

и щгр- граничная частота. При частотах, удовлетворяющих условию

щ<< щгр

среда является проводником, а при

щ>> щгр

- диэлектриком.

Комплексная амплитуда напряжённости поля в среде с потерями энергии

Постоянная распространения в в идеальном диэлектрике определяется выражением (1.8), которое с учётом (1.3) принимает вид

В среде с потерями постоянная распространения становится комплексным числом.

Комплексную постоянную распространения запишем в виде (см. приложение 4)
,
где для диэлектрика с малыми потерями
.(1.16)
Подставив в (1.13) , вместо в, получим
(1.17)
что эквивалентно записи для мгновенных значений

Как видим, по мере распространения волны амплитуда колебаний уменьшается по закону
.
По этой причине б называют коэффициентом затухания среды. Аналогично изменяется и напряжённость магнитного поля

Средняя во времени мощность электромагнитного поля, проходящая через поверхность единичной площади, определяется усреднённым за период колебаний

вектором Пойнтинга.

Подставив сюда E(t,z) и H(t,z), получим

Итак, в среде с потерями плотность мощности плоской электромагнитной волны уменьшается по мере удаления волны от источника со скоростью
, дБ/м
1.9 Радиоволны в проводниках. Скин-эффект
В радиосистеме радиоволны распространяются либо в свободном пространстве, либо в линиях передачи - направляющих системах. Линия передачи представляет собой совокупность проводников и диэлектрика. Волна распространяется в диэлектрике и попадает на границу раздела диэлектрик-проводник.

В результате возникает волна, отражённая и преломлённая, уходящая вглубь проводника. Можно показать, что в проводниках угол преломления в≈0, независимо от угла падения, т.е. преломленная волна уходит в проводник почти по нормали к границе раздела сред (рис. 1.5)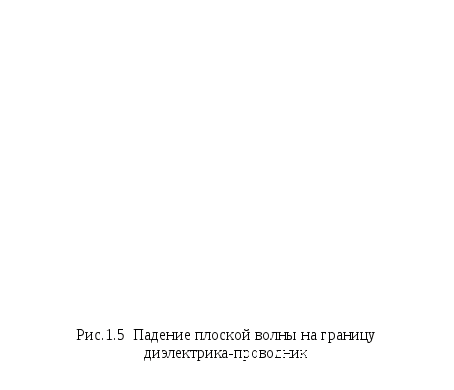


На рисунке 1.5: -вектор Пойнтинга падающей волны, - отражённой волны, - преломлённой волны.

На рисунке 1.6 показана часть проводника и направления координатных осей.

Составляющая напряжённости электрического поля E, касательная к границе раздела сред, имеет на границе амплитуду колебания E. В соответствии с (1.17), комплексная амплитуда зависит от координаты y следующим образом:
(1.18)
Коэффициент затухания в проводнике (см. приложение 4)
(1.19)
В проводнике б значительно выше, чем в диэлектрике, поэтому амплитуда колебаний Е быстро уменьшается по мере проникновения поля в глубину проводника. То же действительно и для напряжённости магнитного поля Н. В результате, в проводнике электромагнитное поле расположено в достаточно тонком поверхностном слое.

Глубину проникновения поля в проводнике оценивают глубиной скин-слоя h, т.е. величиной y = h, при которой амплитуда колебаний поля уменьшается в е раз, по сравнению со значением на поверхности. Из (1.18) следует, что глубина скин-слоя
(1.20)
или, с учётом (1.19)
(1.21)
где f-частота колебаний поля,

магнитная проницаемость, g-электропроводность проводника.

Сопротивление проводника переменному ноку.

В результате того, что напряжённость электрического поля сосредоточена вблизи поверхности проводника, переменный электрический ток протекает в относительно узком приповерхностном слое, что следует из закона Ома: . В результате, сопротивление переменному току оказывается выше, чем постоянному.

Получим выражение для сопротивления отрезка проводника длинной l, шириной d и бесконечной глубиной (координата y меняется от 0 до ∞). В соответствии с (1.18), плотность тока

Комплексная амплитуда тока, проходящего через поперечное сечение проводника шириной б и бесконечной глубиной

или

Комплексная амплитуда напряжения на проводнике длиной
,
Отсюда сопротивление проводника

Как видим, сопротивление Z имеет действительную часть

и мнимую часть индуктивного характера

Учитывая (1.20), получим, что активное сопротивление проводника переменному току
(1.22)
равно сопротивлению проводника постоянному току, если высота проводника h=hск.

Как следует из (1.22), при изготовлении проводников для переменного тока толщину металлизации нецелесообразно устанавливать существенно больше hск. На практике толщину металлизации выбирают с запасом в пределах h=(2...3)hск
2. Радиоволны в линиях передачи
Для передачи энергии электромагнитного поля от передатчика к передающей антенне, от приемной антенны к приемнику, от каскада к каскаду в радиосистеме применяют линии передачи. Иначе их называют фидерные линии от английского слова feed– питать. Например, фидерная линия, ведущая от генератора электромагнитных колебаний к антенне – это линия, питающая антенну электромагнитной энергией.
2.1 Типы передающих линий
В современных радиосистемах используют, в основном, четыре типа передающих линий – двухпроводную, коаксиальную, микрополосковую и волноводную – рис.2.1.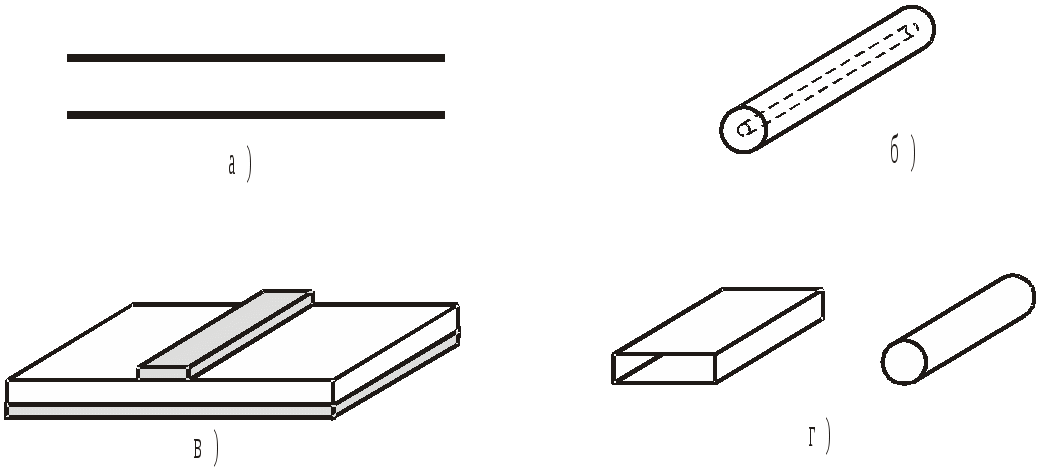






Рис.2.1. Типы линий передачи

а) двухпроводная; б) коаксиальная;

в) микрополосковая; г) волновод – прямоугольный и круглый.




Простейшей линией является двухпроводная – это два параллельных металлических проводника. Если один провод расположен внутри другого, получается коаксиальная линия, или коаксиальный кабель. В каскадах СВЧ применяют микрополосковую линию (МПЛ), а также волноводы – трубы прямоугольного и круглого сечения. МПЛ – это два параллельных проводника - узкий и широкий, разделенных диэлектрической подложкой.

В линиях передачи электромагнитное поле существует в пространстве около проводников, а сами проводники подобны рельсам, задающим направление движения энергии поля.

Пространство между проводниками и линией может быть ничем не заполненным. В этом случае линии являются воздушными. Если между проводниками имеется диэлектрик, то это линия с диэлектрическим заземлением.

Для того, чтобы определить структуру электромагнитного поля в линии передачи, рассмотрим модель, справедливую для всех типов линий – это две параллельные бесконечные плоскости – рис.2.2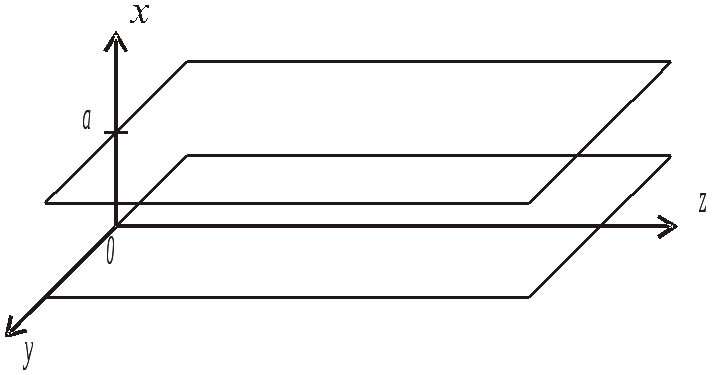




Р
Рис.2.2. Модель передающей линии

ешим уравнения Максвелла для линии передачи, образованной двумя параллельными плоскостями, при следующих допущениях:

1) плоскости идеально проводящие, т.е. удельная электропроводность материала плоскости ;

2) диэлектрик между плоскостями идеальный, т.е. его удельная электропроводность ;

ищем решение в виде волн, распространяющихся вдоль оси z;

вдоль оси y плоскости бесконечны и электромагнитное поле вдоль этой оси не меняется;

линия возбуждается источником монохроматического поля.

При сделанных допущениях 1-е и 2-е уравнения Максвелла для комплексных амплитуд имеют следующий вид:


Раскрывая их и учитывая, что производные составляющих поля по оси y равны 0, получим 2 системы уравнений – первая относительно переменных ,,
,
; (2.1)
,
вторая - относительно переменных , ,

(2.2)

Система уравнений (2.1) описывает поля, у которых вектор напряженности магнитного поля перпендикулярен направлению распространения z, в то время, как вектор имеет проекцию на ось z. Такие поля называют поперечно магнитными, или поля TM – типа (Transverse Magnetic Waves). Иначе их называют полями E – типа.

Система (2.2) относится к поперечно – электрическим полям (Transverse Electrical Waves), т.е. полям ТЕ – типа (или полям H), поскольку здесь вектор напряженности электрического поля 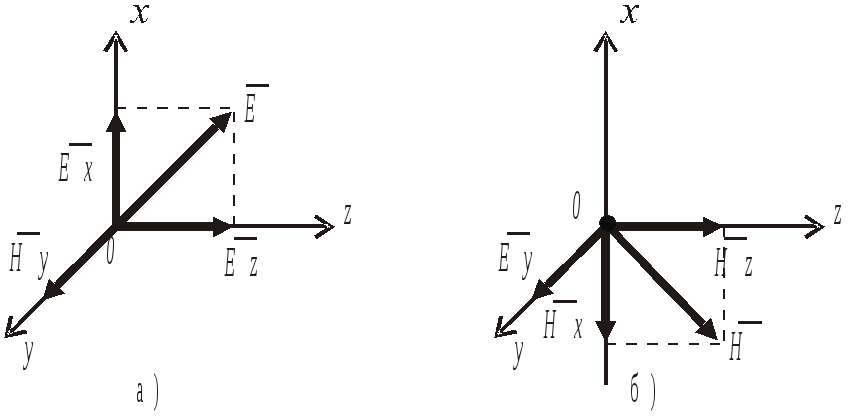перпендикулярен направлению распространения z - рис. 2.3. Рассмотрим структуру полей различных типов более подробно.






Рис.2.3. Возможные типы полей в передающих линиях:

а) ТН - волны; б) ТЕ - волны




2.2 Поперечно- магнитные волны
Из системы (2.1) исключим и и составим одно уравнение относительно
(2.3)
Получим уравнение эллиптического типа, для однозначного решения которого требуется задание граничных параметров [2].

Рассматриваемая линия передачи ограничена плоскостями, расположенными при следующих значениях координаты x: x = 0 и x = a.

На границе с проводником вектор р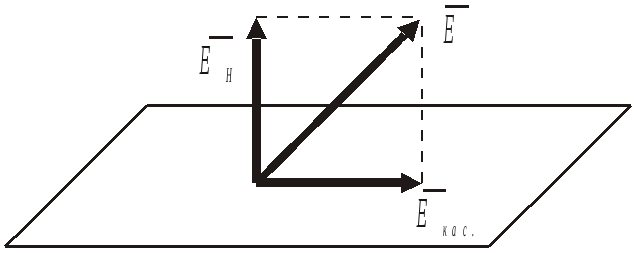асположен таким образом, что может быть представлен суммой нормальной Eн и касательной Eкас составляющих-рис.2.4 диэлектрик.
Р
ис. 2.4. Электрическое поле на границе диэлектрик-проводник.
Наличие касательной составляющей электрического поля вызывает появление электрического тока плотностью
,
где - удельная электропроводность проводника.

Поскольку плотность тока конечна, а проводимость идеального проводника, то нужно выполнение условия при x = 0, x = a. В соответствии со вторым – уравнением системы (2.1) граничные условия для уравнения (2.3) запишем следующим образом:
, при x = 0, x = a.(2.4)
В приложении 5 получено решение уравнения (2.3) с граничными условиями (2.4). При отсутствии отражений оно может быть записано в следующем общем виде:

где - амплитуда напряженности магнитного поля прямой волны при z = 0 (m = 0, 1, 2, 3, …..),
,
.
При выполнении условия имеем
,
где

,
или